6.5. Control System Signals

One or more sequences of user-defined signals are used to define a control-system block diagram. The four types of signals are measured, demand, block, and control. Each is described in the sections that follow. Detailed information on the input requirements is provided in the Appendix.

6.5.1. Measured Signals

Measured signals represent the value of plant-state variables, such as pressure, temperature, or flow rate. Measured signals are implemented in SAS as a virtual data acquisition system (DAS). Unless otherwise noted, measured signal values are obtained at the beginning of a PRIMAR time step. These values are used to update the control system state in effect during the time step. That state is then reported along with other simulation output at the end of the time step.

6.5.2. Demand Signals

Demand signals represent the value of an external, time-dependent load. Demand signals are interpolated from a table of user-defined (time,value) pairs, where the values are assumed to be normalized to an initial-condition value.

6.5.3. Block Signals

Block signals represent mathematical or logical operations that define the control system’s behavior. Input to block signals comes from measured, demand, or other block signals.

6.5.3.1. Variable Lag Compensator

Note

New in Version 5.3.

Theory

A variable lag compensator is similar to the lag compensator except that the delay time parameter, \(\tau\), can vary during the Control System simulation. An equation that expresses this behavior is

\[y\left( t \right) + \tau\left( t \right)\frac{dy}{dt} = u\left( t \right)\]

where

\(u\left( t \right)\) = input driving function

\(\tau\left( t \right)\) = delay (lag)

\(y\left( t \right)\) = output function result

Assuming that the lag time is always positive, a solution to the above equation is

\[y\left( t \right) = y_{0}e^{- \int_{0}^{t}\frac{dt'}{\tau\left( t \right)}} + e^{- \int_{t_{0}}^{t}\frac{dt'}{\tau\left( t \right)}}\int_{0}^{t}{\frac{u\left( t' \right)}{\tau\left( t' \right)}e^{\int_{t_{0}}^{t'}\frac{dt''}{\tau\left( t'' \right)}}dt'}\]

where \(y_{0} = y\left( 0 \right)\) and \(t_{0}\) is an arbitrary integration constant.

The complexity of the above solution can be simplified if we assume the input driving function and delay function are linear functions of time: \(u\left( t \right) = u_{0} + u't\) and \(\tau\left( t \right) = \tau_{0} + \tau't\), respectively. With this assumption, the solution becomes

\[y\left( t \right) = y_{0}\left( 1 + \frac{\tau'}{\tau_{0}}t \right)^{- \frac{1}{\tau'}} + u_{0}\left\lbrack 1 - \left( 1 + \frac{\tau'}{\tau_{0}}t \right)^{- \frac{1}{\tau'}} \right\rbrack + \frac{u'}{1 + \tau'}\left\lbrack t - \tau_{0}\left\lbrack 1 - \left( 1 + \frac{\tau'}{\tau_{0}}t \right)^{- \frac{1}{\tau'}} \right\rbrack \right\rbrack\]

If \(\tau\) is slowly varying with time and we take the limit that \(\tau' \rightarrow 0\), we arrive at the solution for a constant \(\tau\) during the time interval:

\[y\left( t \right) = y_{0}e^{- \frac{t}{\tau}_{0}} + u_{0}\left( 1 - e^{- \frac{t}{\tau_{0}}} \right) + u'\left\lbrack t - \tau_{0}\left( 1 - e^{- \frac{t}{\tau_{0}}} \right) \right\rbrack\]

Implementation

The analytic solution for the variable lag compensator can be used to solve for the value of \(y_{1} = y\left( t_{0} + \Delta t \right)\) at the end of a Control System sub-interval (time step) given the initial value \(y_{0} = y\left( t_{0} \right)\). Knowing the lag time at the beginning of the time step, \(\tau_{0}\), and the input driving function at the beginning and end of the time step, \(u_{0} = u\left( t_{0} \right)\) and \(u_{1} = u\left( t_{0} + \Delta t \right)\), respectively, then the solution for \(y_{1}\) at the end of the time step is

\[y_{1} = y_{0}e^{- \delta} + u_{0}\left( 1 - e^{- \delta} \right) + \left( u_{1} - u_{0} \right)\left\lbrack 1 - \frac{1 - e^{- \delta}}{\delta} \right\rbrack\]

where \(\delta = \frac{\Delta t}{\tau_{0}}\).

Because this solution is prone to numerical round-off errors, expansions for the exponential function are used:

\[e^{- \delta} = 1 - \delta + \frac{\delta^{2}}{2} - \frac{\delta^{3}}{6} + O\left\lbrack \delta^{4} \right\rbrack\]

and

\[\frac{1 - e^{- \delta}}{\delta} = 1 - \frac{\delta}{2} + \frac{\delta^{2}}{6} - \frac{\delta^{3}}{24} + O\left\lbrack \delta^{4} \right\rbrack\]

Using these expansions, the solution is written as

\[y_{1} = y_{0}\left\lbrack 1 - \delta + \frac{\delta^{2}}{2} \right\rbrack + u_{0}\left\lbrack \frac{\delta}{2} - \frac{\delta^{2}}{3} \right\rbrack + u_{1}\left\lbrack \frac{\delta}{2} - \frac{\delta^{2}}{6} \right\rbrack + O\left\lbrack \delta^{3} \right\rbrack\]

To minimize numerical round-off errors in the code, the following form is used:

\[y_{1} \approx y_{0}\left\lbrack 1 - \delta\left( 1 - \delta\left( \frac{1}{2} \right) \right) \right\rbrack + u_{0}\left\lbrack \delta\left( \frac{1}{2} - \delta\left( \frac{1}{3} \right) \right) \right\rbrack + u_{1}\left\lbrack \delta\left( \frac{1}{2} - \delta\left( \frac{1}{6} \right) \right) \right\rbrack\]

which is second-order accurate in \(\delta\). This form also avoids the need to make expensive exponential function evaluations.

Use

A variable lag compensator is identified in the Control System input as signal type ITYPE = 23. It requires two input signals to define the time-dependent functions \(u\left( t \right)\) and \(\tau\left( t \right)\). These are identified by the input parameters J1 and J2, respectively. Input for the variable lag compensator is summarized in the table below.

Input	Description
ISIG	User-defined signal number
ITYPE = 23	Variable Lag Compensator type
J1	Signal # of driving function, \(u(t)\)
J2	Signal # of delay time, \(\tau\left( t \right)\)
F1	Multiplier for driving function [default: 1]
F2	(unused)
F3	(unused)
F4	Steady-state initial condition, \(y\left( 0 \right)\) [default: \(y\left( 0 \right) = u\left( 0 \right)\)]
F5	Zero-crossing parameter (F5 > 0)

The input includes two optional parameters, F1 and F4, and one required parameter, F5. If the optional parameters are blank or zero, defaults will be applied as indicated in the table. For example, if F1 is non-zero, then the actual driving function will include a multiplier:

\[u\left( t \right) = \mathrm{F1} \times \mathrm{\text{sig}}\left( \mathrm{J1} \right)\]

Likewise, if F4 is non-zero, it is used to define the initial steady-state condition as \(y\left( 0 \right) = \mathrm{F4}\). Otherwise, the steady-state solution to the equation is \(y\left( 0 \right) = u\left( 0 \right)\).

The zero-crossing parameter, F5, is used in the same manner as with other Control System signals to stabilize convergence testing when the solution for \(y\left( t \right)\) is near zero. The normalized error is approximated as follows to avoid divide-by-zero errors:

\[\mathrm{\text{error}} = \left| \frac{\Delta y}{y} \right| \cong \frac{\left| \Delta y \right|}{\left| y \right| + \mathrm{F5}}\]

Therefore, users can select a value for F5 that is small enough to ensure convergence when \(y\left( t \right)\) is small, but large enough to avoid excessive iterations when small values for \(y\left( t \right)\) do not have a significant impact on the overall solution.

Like the lag compensator, the variable lag compensator shifts both the phase and amplitude of the input signal \(u\left( t \right)\). However, the phase and amplitude vary as a function of time through the additional input for \(\tau\left( t \right)\). To demonstrate this, consider the following conditions:

\[\begin{split}u\left( t \right) &= \sin\left( \frac{2\pi}{5}t \right) \\ \tau\left( t \right) &= 1.9\sin\left( \frac{2\pi}{50}t \right) + 2 \\ y\left( 0 \right) &= 2 \\\end{split}\]

These can be represented in the Control System input as follows:

INCONT     5

# Time: t
1 -55 0 0 0.0 0.0 0.0 0.0 0.0

# Driving Signal: Sin(2πt/5)
11 22 1 0 1.0 1.2566370 0.0 0.0

# Lag Time Variation: Sin(2πt/50)
12 22 1 0 1.0 .12566370 0.0 0.0

# Constant: 2
13 21 0 0 2.0 0.0 0.0 0.0 0.0

# Lag Time: 1.9Sin(2πt/50) + 2
17 1 12 13 1.9 1.0 1.0 0.0 0.0

# Variable Lag Compensator(11,17)
# ITYPE J1 J2 F1 F4 F5
18 23 11 17 1.0 0.0 0.0 2.0 0.001

999 1

8001 2 0.00000001 0.00000001

END

Using the above Listing in a SAS4A/SASSYS-1 input file would produce the following Control System output:

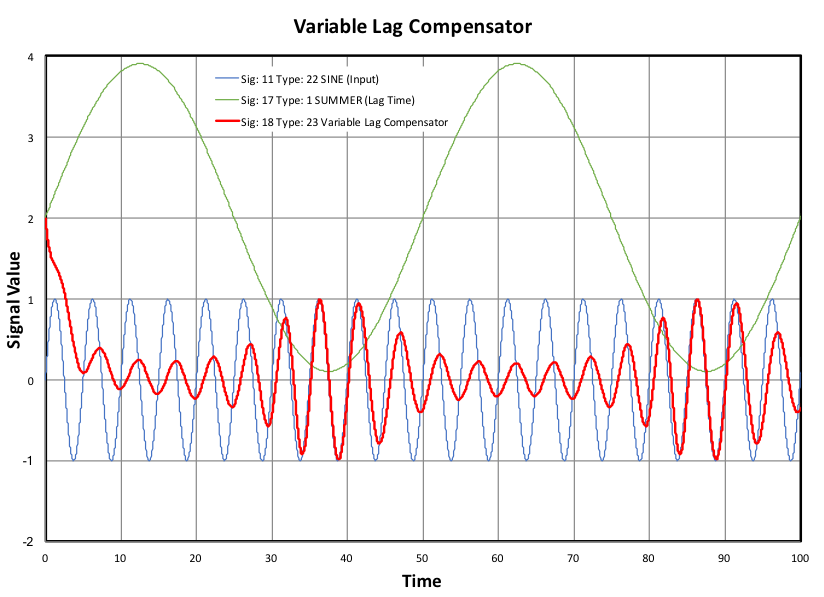
Note that because F4 = 2, the variable lag compensator starts at the non-equilibrium value \(y\left( 0 \right) = 2\). As the lag time \(\tau\left( t \right)\) rises and falls, the delay in the input signal becomes longer and shorter, respectively. Similarly, the amplitude of the output decreases and increases.

6.5.4. Control Signals

Control signals are used to set the value of a SAS variable during the simulation. Currently, a limited number of simulation variables can be controlled. The primary purpose of control signals is to affect reactivity (e.g. scram), pump torque, and valve coefficients.

6.5.4.1. Simulation Trip

The simulation trip control signal (JTYPE=-10) is used to stop the SAS simulation based on the value of an input signal. When the input signal changes from false (a value of zero) to true (a non-zero value), code execution will end at the end of the main time step. Since the input signal is treated as a logical, a large zero crossing parameter (e_z, entered in F6SIG) is recommended to avoid control system cutbacks. A value of 1E+09 is suggested.

The control system trips the simulation by setting the maximum number of time steps to the current main time step number when the input signal triggers the trip. To restart from a case that was ended by the simulation trip control signal, the user should reset MAXSTP in the restart case input file to the desired value so that the simulation can continue.

A simulation trip control signal can be configured as unlatched (J2SIG = 0) or latched (J2SIG = 1). An unlatched simulation trip control signal is capable of tripping the simulation again after a restart, while a latched simulation trip control signal cannot.