5.16. Appendices

5.16.1. Appendix 5.1: IHX Matrix Coefficients

The coefficients in Eq. (5.4-37) for the \(j\)-th vertical section of the shell in terms of the quantities defined in Section 5.4.2.2 are as follows:

(A5.1‑1)

\[a_{1} \left( j \right) = \left( \rho c \right)_{\text{SH}} d_{\text{SH}} + \theta_{2\text{S}} \Delta t H_{\text{S}}\left( j \right) + \theta_{2\text{S}} \Delta t \frac{\left( hA \right)_{\text{snk}}}{P_{\text{S}}}\]

(A5.1‑2)

\[a_{2} \left( j \right) = - \frac{1}{2} \theta_{2\text{S}} \Delta t H_{\text{S}}\left( j \right)\]

(A5.1‑3)

\[a_{3} \left( j \right) = - \frac{1}{2} \theta_{2\text{S}} \Delta t H_{\text{S}}\left( j \right)\]

(A5.1‑4)

\[a_{4} \left( j \right) = - \Delta t H_{\text{S}}\left( j \right) T_{\text{SH}3}\left( j \right) + \Delta t H_{\text{S}}\left( j \right) {\overline{T}}_{\text{CS}3}\left( j \right) + \frac{\Delta t\left( hA \right)_{\text{snk}} \left\lbrack T_{\text{snk}} - T_{\text{SH}3}\left( j \right) \right\rbrack}{P_{\text{S}}}\]

(A5.1‑5)

\[{\overline{T}}_{\text{CP}3} \left( j \right) = \frac{1}{2} \left\lbrack T_{\text{CS}3}\left( j \right) + T_{\text{CS}3}\left( j + 1 \right) \right\rbrack\]

where

\(\theta_{2\text{S}}\) = the degree of implicitness for the shell-side coolant channel

\(\Delta t\) = the time interval

The coefficients in Eq. (5.4-38) for the \(j\)-th vertical section of the shell-side coolant for normal flow (downward) are:

(A5.1‑6)

\[\begin{split} e_{1} \left( j \right) = \frac{1}{2} A_{\text{c}} {\overline{\rho}}_{\text{CS}}\left( j \right) {\overline{c}}_{\text{CS}}\left( j \right) + \Delta t \frac{{\overline{c}}_{\text{CS}}\left( j \right)}{\Delta z\left( j \right)} \theta_{2\text{S}} \left| w_{\text{S}4} \right| \\ + \Delta t P_{\text{S}} H_{\text{S}}\left( j \right) \frac{1}{2} \theta_{2\text{S}} + \Delta t S P_{\text{ST}} H_{\text{ST}}\left( j \right) \frac{1}{2} \theta_{2\text{S}}\end{split}\]

(A5.1‑7)

\[e_{2}\left( j \right) = 0\]

(A5.1‑8)

\[e_{3}\left( j \right) = - \Delta t P_{\text{S}} H_{\text{S}}\left( j \right) \theta_{2\text{S}}\]

(A5.1‑9)

\[e_{4}\left( j \right) = 0\]

(A5.1‑10)

\[e_{5}\left( j \right) = - \Delta t S P_{\text{ST}} H_{\text{ST}}\left( j \right) \theta_{2\text{S}}\]

(A5.1‑11)

\[e_{6}\left( j \right) = 0\]

(A5.1‑12)

\[\begin{split} e_{7}\left( j \right) = \frac{1}{2} A_{\text{CS}} {\overline{\rho}}_{\text{CS}}\left( j \right) {\overline{c}}_{\text{CS}}\left( j \right) - \Delta t \frac{{\overline{c}}_{\text{CS}}\left( j \right)}{ \Delta z\left( j \right)} \theta_{2\text{S}} \left| \ w_{\text{S}4} \right| \\ + \Delta t P_{\text{S}} H_{\text{S}}\left( j \right) \frac{1}{2} \theta_{2\text{S}} + \Delta t S P_{\text{ST}} H_{\text{ST}}\left( j \right) \frac{1}{2} \theta_{2\text{S}}\end{split}\]

(A5.1‑13)

\[\begin{split} e_{8}\left( j \right) = - \Delta t \frac{{\overline{c}}_{\text{CS}}\left( j \right)}{ \Delta z\left( j \right)} \left\{ \theta_{1\text{S}} \left| \ w_{\text{S}3} \right| + \theta_{2\text{S}} \left| w_{\text{S}4} \right| \left\lbrack T_{\text{CS}3}\left( j \right) - T_{\text{CS}3}\left( j + 1 \right) \right\rbrack \right\} \\ + \Delta t P_{\text{S}} H_{\text{S}}\left( j \right) \left\{ T_{\text{SH}3}\left( j \right) - \frac{1}{2} \left\lbrack T_{\text{CS}3}\left( j \right) + T_{\text{CS}3}\left( j + 1 \right) \right\rbrack \right\} \\ + \Delta t S P_{\text{S}} H_{\text{ST}}\left( j \right) \left\{ T_{\text{TU}3}\left( j \right) - \frac{1}{2} \left\lbrack T_{\text{CS}3}\left( j \right) + T_{\text{CS}3}\left( j + 1 \right) \right\rbrack \right\}\end{split}\]

The same coefficients for reversed flow (upward) in the shell-side coolant channel are:

(A5.1‑14)

\[\begin{split} e\left( j \right) = \frac{1}{2} A_{\text{CS}} {\overline{\rho}}_{\text{CS}}\left( j - 1 \right) {\overline{c}}_{\text{CS}}\left( j - 1 \right) + \Delta t \frac{{\overline{c}}_{\text{CS}}\left( j - 1 \right)}{\Delta z \left( j - 1 \right)} \theta_{2\text{S}} \left| w_{\text{S}4} \right| \\ + \Delta t P_{\text{S}} H_{\text{S}}\left( j - 1 \right) \frac{1}{2} \theta_{2\text{S}} + \Delta t S P_{\text{ST}} H_{\text{ST}}\left( j - 1 \right) \frac{1}{2} \theta_{2\text{S}}\end{split}\]

(A5.1‑15)

\[e_{2}\left( j \right) = - \Delta t P_{\text{S}}H_{\text{S}}\left( j - 1 \right) \theta_{2\text{S}}\]

(A5.1‑16)

\[e_{3}\left( j \right) = 0\]

(A5.1‑17)

\[e_{4}\left( j \right) = - \Delta t S P_{\text{ST}} H_{\text{ST}}\left( j - 1 \right) \theta_{2\text{S}}\]

(A5.1‑18)

\[e_{5}\left( j \right) = 0\]

(A5.1‑19)

\[\begin{split} e_{6}\left( j \right) = \frac{1}{2} A_{\text{CS}} {\overline{\rho}}_{\text{CS}}\left( j - 1 \right) {\overline{c}}_{\text{CS}}\left( j - 1 \right) - \Delta t \frac{{\overline{c}}_{\text{CS}}\left( j - 1 \right)}{\Delta z\left( j - 1 \right)} \theta_{2\text{S}} \left| w_{\text{S}4} \right| \\ + \Delta t P_{\text{S}} H_{\text{S}}\left( j - 1 \right) \frac{1}{2} \theta_{2\text{S}} + \Delta t S P_{\text{ST}} H_{\text{ST}}\left( j - 1 \right) \frac{1}{2} \theta_{2\text{S}}\end{split}\]

(A5.1‑20)

\[e_{7}\left( j \right) = 0\]

(A5.1‑21)

\[\begin{split} e_{8}\left( j \right) = - \Delta t \frac{{\overline{c}}_{\text{CS}}\left( j - 1 \right)}{\Delta z\left( j - 1 \right)} \left\{ \left( \theta_{1\text{S}} \left| w_{\text{S}3} \right| + \theta_{2\text{S}} \left| w_{\text{S}4} \right| \right) \left\lbrack T_{\text{CS}3}\left( j \right) - T_{\text{CS}3}\left( j - 1 \right) \right\rbrack \right\} \\ + \Delta t P_{\text{S}} H_{\text{S}}\left( j - 1 \right) \left\{ T_{\text{SS}3}\left( j - 1 \right) - \frac{1}{2} \left\lbrack T_{\text{CS}3}\left( j - 1 \right) + T_{\text{CS}3}\left( j \right) \right\rbrack \right\} \\ + \Delta t S P_{\text{ST}}\left( j - 1 \right) \left\{ T_{\text{TU}3}\left( j - 1 \right) - \frac{1}{2} \left\lbrack T_{\text{CS}3}\left( j - 1 \right) + T_{\text{CS}3}\left( j \right) \right\rbrack \right\}\end{split}\]

The terms \(e_{9} \left( j \right)\) and \(e_{10} \left( j \right)\) have been added to Eq. (5.4-38) because they appear during the solution of the simultaneous equations. These arrays are set to zero before the solution is begun.

In addition, the boundary conditions for normal shell-side coolant channel flow are

(A5.1‑22)

\[\begin{align} e_{1}\left( jm \right) = 1; && e_{2,3,4,5,6,7} \left( jm \right) = 0; && e_{8}\left( jm \right) = \Delta T_{\text{CS}}\left( jm \right) \end{align}\]

For reversed primary channel flow, they are

(A5.1‑23)

\[\begin{align} e_{1}\left( 1 \right) = 1; && e_{2,3,4,5,6,7}\left( 1 \right) = 0; && e_{8}\left( 1 \right) = \Delta T_{\text{CS}}\left( 1 \right) \end{align}\]

and for both cases, they are

(A5.1‑24)

\[\begin{split} \begin{align} e_{2}\left( 1 \right) = 0; && e_{4}\left( 1 \right) = 0; && e_{6}\left( 1 \right) = 0; \\ e_{3}\left( jm \right) = 0; && e_{5}\left( jm \right) = 0; && e_{7}\left( jm \right) = 0 \end{align}\end{split}\]

The coefficients in Eq. (5.4-39) for the \(j\)-th vertical section of the tube are:

(A5.1‑25)

\[\begin{split} c_{1}\left( j \right) = \left( \rho c \right)_{\text{TU}} \frac{1}{2} \left( P_{\text{ST}} + P_{\text{TT}} \right) d_{\text{TU}} + \Delta t \theta_{2\text{S}} P_{\text{ST}} H_{\text{ST}}\left( j \right) \\ + \Delta t \theta_{\text{ST}} P_{\text{TT}} H_{\text{TT}}\left( j \right)\end{split}\]

(A5.1‑26)

\[c_{2}\left( j \right) = - \frac{1}{2} \Delta t \theta_{2\text{S}} P_{\text{ST}} H_{\text{ST}}\left( j \right)\]

(A5.1‑27)

\[c_{3}\left( j \right) = - \frac{1}{2} \Delta t \theta_{2\text{S}} P_{\text{ST}} H_{\text{ST}}\left( j \right)\]

(A5.1‑28)

\[c_{4}\left( j \right) = - \frac{1}{2} \Delta t \theta_{2\text{T}} P_{\text{TT}} H_{\text{TT}}\left( j \right)\]

(A5.1‑29)

\[c_{5}\left( j \right) = - \frac{1}{2} \Delta t \theta_{2\text{T}} P_{\text{TT}} H_{\text{TT}}\left( j \right)\]

(A5.1‑30)

\[\begin{split} c_{6}\left( j \right) = - \Delta t \left\lbrack P_{\text{ST}} H_{\text{ST}}\left( j \right) + P_{\text{TT}} H_{\text{TT}}\left( j \right) \right\rbrack T_{\text{TU}3}\left( j \right) \\ + \Delta t P_{\text{ST}} H_{\text{ST}}\left( j \right) \frac{1}{2}\left\lbrack T_{\text{CS}3}\left( j \right) + T_{\text{CS}3}\left( j + 1 \right) \right\rbrack \\ + \Delta t P_{\text{TT}} H_{\text{TT}}\left( j \right) \frac{1}{2}\left\lbrack T_{\text{CT}3}\left( j \right) + T_{\text{CT}3}\left( j + 1 \right) \right\rbrack\end{split}\]

The coefficients in Eq. (5.4-40) for the \(j\)-th vertical section of the tube-side coolant for normal flow (upward) are:

(A5.1‑31)

\[\begin{split} f_{1}\left( j \right) = \frac{1}{2} A_{\text{CT}} {\overline{\rho}}_{\text{CT}}\left( j - 1 \right) {\overline{c}}_{\text{CT}}\left( j - 1 \right) + \Delta t \frac{{\overline{c}}_{\text{CT}}\left( j - 1 \right)}{\Delta z\left( j - 1 \right) S} \left| w_{\text{T}4} \right| \theta_{2\text{T}} \\ + \Delta t P_{\text{TT}} H_{\text{TT}}\left( j - 1 \right) \frac{1}{2} \theta_{2\text{T}}\end{split}\]

(A5.1‑32)

\[f_{2}\left( j \right) = - \Delta t P_{\text{TT}} H_{\text{TT}}\left( j - 1 \right) \theta_{2\text{T}}\]

(A5.1‑33)

\[f_{3}\left( j \right) = 0\]

(A5.1‑34)

\[\begin{split} f_{4} \left( j \right) = \frac{1}{2} A_{\text{CT}} {\overline{\rho}}_{\text{CT}}\left( j - 1 \right) - \Delta t \frac{{\overline{c}}_{\text{CT}}\left( j - 1 \right)}{\Delta z \left( j - 1 \right) S} \left| w_{\text{T}4} \right| \theta_{2\text{T}} \\ + \Delta t P_{\text{TT}} H_{\text{TT}} \left( j - 1 \right) \frac{1}{2} \theta_{2\text{T}}\end{split}\]

(A5.1‑35)

\[f_{5}\left( j \right) = 0\]

(A5.1‑36)

\[\begin{split} f_{6}\left( j \right) = - \Delta t \frac{{\overline{c}}_{\text{CT}}\left( j - 1 \right)}{\Delta z\left( j - 1 \right) S} \left\{ \left( \left| w_{\text{T}3} \right| \theta_{1\text{T}} + \left| w_{\text{T}4} \right| \theta_{2\text{T}} \right) \left\lbrack T_{\text{CT}3}\left( j \right) - T_{\text{CT}3}\left( j - 1 \right) \right\rbrack \right\} \\ + \Delta t P_{\text{TT}} H_{\text{TT}}\left( j - 1 \right) \left\{ T_{\text{TU}3}\left( j - 1 \right) - \frac{1}{2} \left\lbrack T_{\text{CT}3}\left( j - 1 \right) + T_{\text{CT}3}\left( j \right) \right\rbrack \right\}\end{split}\]

The same coefficients for reversed flow (downward) in the intermediate coolant channel are:

(A5.1‑37)

\[\begin{split} f_{1}\left( j \right) = \frac{1}{2} A_{\text{CT}} {\overline{\rho}}_{\text{CT}}\left( j \right) {\overline{c}}_{\text{CT}}\left( j \right) + \Delta t \frac{{\overline{c}}_{\text{I}}\left( j \right)}{\Delta z\left( j \right) S} \left| \ w_{\text{T}4} \right| \theta_{2\text{T}} \\ + \Delta t P_{\text{TT}} H_{\text{TT}}\left( j \right) \theta_{2\text{T}}\end{split}\]

(A5.1‑38)

\[f_{2}\left( j \right) = 0\]

(A5.1‑39)

\[f_{3}\left( j \right) = - \Delta t P_{\text{TT}} H_{\text{TT}}\left( j \right) \theta_{2\text{T}}\]

(A5.1‑40)

\[f_{4}\left( j \right) = 0\]

(A5.1‑41)

\[\begin{split} f_{5}\left( j \right) = \frac{1}{2} A_{\text{CT}} {\overline{\rho}}_{\text{CT}}\left( j \right) {\overline{c}}_{\text{CT}}\left( j \right) - \Delta t \frac{{\overline{c}}_{\text{CT}}\left( j \right)}{\Delta z\left( j \right) S} \left| \ w_{\text{T}4} \right| \theta_{2\text{T}} \\ + \Delta t P_{\text{TT}} H_{\text{TT}}\left( j \right) \frac{1}{2} \theta_{2\text{T}}\end{split}\]

(A5.1‑42)

\[\begin{split} f_{6}\left( j \right) = - \Delta t \frac{{\overline{c}}_{\text{CT}}\left( j \right)}{\Delta z\left( j \right) S} \left\{ \left( \left| w_{\text{T}3} \right| \theta_{1\text{T}} + \left| w_{\text{T}4} \right| \theta_{2\text{T}} \right) \left\lbrack T_{\text{CT}3}\left( j \right) - T_{\text{CT}3}\left( j + 1 \right) \right\rbrack \right\} \\ + \Delta t P_{\text{TT}} H_{\text{TT}}\left( j \right) \left\{ T_{\text{TU}3}\left( j \right) - \frac{1}{2} \left\lbrack T_{\text{CT}3}\left( j \right) + T_{\text{CT}3}\left( j + 1 \right) \right\rbrack \right\}\end{split}\]

The terms for \(f_{7} \left( j \right)\) and \(f_{8} \left( j \right)\) have been added to Eq. (5.4-40) because they appear during the solution of the simultaneous equations. These arrays are also set to zero before the solution is begun.

Also, the boundary conditions for normal tube-side coolant channel flow are

(A5.1‑43)

\[\begin{align} f_{1}\left( 1 \right) = 1; && f_{2,3,4,5}\left( 1 \right) = 0; && f_{6}\left( 1 \right) = \Delta T_{\text{CT}}\left( 1 \right) \end{align}\]

For reversed tube-side channel flow, they are

(A5.1‑44)

\[\begin{align} f_{1}\left( j\max \right) = 1; && f_{2,3,4,5}\left( j\max \right) = 0; && f_{6}\left( j\max \right) = \Delta T_{\text{CT}}\left( j\max \right) \end{align}\]

and for both cases, they are

(A5.1‑45)

\[\begin{split} \begin{align} f_{2}\left( 1 \right) = 0; && f_{4}\left( 1 \right) = 0; \\ f_{1}\left( j\max \right) = 0; && f_{5}\left( j\max \right) = 0 \end{align}\end{split}\]

5.16.2. Appendix 5.2: IHX Matrix Solution Algorithm

The solution of the matrix represented by Eqs. Eq. (5.4-37) through Eq. (5.4-40) and whose coefficients are given in Section 5.16.1 is accomplished by Gaussian elimination, making use of the zeros present in the matrix. It is presented as an algorithm as it is coded in subroutine TSIHX. The arrows in the following mean replacement of what is on the left by the expression on the right.

\(\text{JMAX}\) = the number of nodes in the primary and intermediate coolant

\(\text{JMAX} - 1\) = the number of nodes in the shell and tube

1. Set \(j\) = 1.

2. Multiply Eq. (5.4-37) by \(\frac{1}{a_{1} \left( j \right)}\)

\(a_{2}\left( j \right) \rightarrow \frac{a_{2}\left( j \right)}{a_{1}\left( j \right)};a_{3}\left( j \right) \rightarrow \frac{a_{3}\left( j \right)}{a_{1}\left( j \right)} ;\ a_{4}\left( j \right) \rightarrow \frac{a_{4}\left( j \right)}{a_{1}\left( j \right)};a_{5} = \frac{a_{5}\left( j \right)}{a_{1}\left( j \right)};\ a_{1}\left( j \right) \rightarrow 1\);

3. \(e_{1}\left( j \right) \rightarrow e_{1}\left( j \right) - e_{3}\left( j \right)a_{2}\left( j \right)\)

\(e_{7}\left( j \right) \rightarrow e_{7}\left( j \right) - \ e_{3}\left( j \right)a_{3}\left( j \right)\);

\(e_{8}\left( j \right) \rightarrow e_{8}\left( j \right) - e_{8}\left( j \right)e_{4}\left( j \right)\);

\(e_{3}\left( j \right) \rightarrow 0\);

4. Multiply non-zero coefficients in Eq. (5.4-38) by \({1}{e_{1} \left( j \right)}\).

\(e_{5}\left( j \right) \ \longrightarrow \ \ \frac{e_{5}\left( j \right)}{e_{1}\left( j \right)} \ ;\ \ e_{7}\left( j \right) \longrightarrow \ \ \frac{e_{7}\left( j \right)}{e_{1}\left( j \right)} \ ;\)

\(e_{8}\left( j \right) \ \longrightarrow \ \ \frac{e_{8}\left( j \right)}{e_{1}\left( j \right)} \ ;\ \ e_{10}\left( j \right) \longrightarrow \ \ \frac{e_{10}\left( j \right)}{e_{1}\left( j \right)}\)

\(e_{1}\left( j \right) \ \longrightarrow \ \ 1\)

\(c_{1}\left( j \right) \ \longrightarrow \ \ c_{1}\left( j \right) \ - c_{2}\left( j \right) e_{5}\left( j \right)\)

\(c_{3}\left( j \right) \ \longrightarrow \ \ c_{3}\left( j \right) \ - c_{2}\left( j \right) e_{7}\left( j \right)\)

\(c_{4}\left( j \right) \ \longrightarrow \ \ c_{4}\left( j \right) \ - c_{2}\left( j \right) e_{10}\left( j \right)\)

\(c_{6}\left( j \right) \ \longrightarrow \ \ c_{6}\left( j \right) \ - c_{2}\left( j \right) e_{8}\left( j \right)\)

\(c_{2}\left( j \right) \ \longrightarrow \ \ 0\)

\(f_{1}\left( j \right) \ \longrightarrow \ \ f_{1}\left( j \right) \ - f_{7}\left( j \right) e_{10}\left( j \right)\)

\(f_{3}\left( j \right) \ \longrightarrow \ \ f_{3}\left( j \right) \ - f_{7}\left( j \right) e_{5}\left( j \right)\)

\(f_{6}\left( j \right) \ \longrightarrow \ \ f_{6}\left( j \right) \ - f_{7}\left( j \right) e_{8}\left( j \right)\)

\(f_{8}\left( j \right) \ \longrightarrow \ \ f_{8}\left( j \right) \ - f_{7}\left( j \right) e_{7}\left( j \right)\)

\(f_{7}\left( j \right) \ \longrightarrow \ \ 0\)

\(e_{1}\left( j + 1 \right) \ \longrightarrow \ \ e_{1}\left( j + 1 \right) \ - e_{6}\left( j + 1 \right) e_{7}\left( j \right)\)

\(e_{4}\left( j + 1 \right) \ \longrightarrow \ \ e_{4}\left( j + 1 \right) \ - e_{6}\left( j + 1 \right) e_{5}\left( j \right)\)

\(e_{8}\left( j + 1 \right) \ \longrightarrow \ \ e_{8}\left( j + 1 \right) \ - e_{6}\left( j + 1 \right) e_{8}\left( j \right)\)

\(e_{9}\left( j + 1 \right) \ \longrightarrow \ \ e_{9}\left( j + 1 \right) \ - e_{6}\left( j + 1 \right) e_{10}\left( j \right)\)

\(e_{6}\left( j + 1 \right) \ \longrightarrow \ \ 0\)

6. Multiply non-zero coefficients in Eq. (5.4-39) by \(\frac{1}{c_{1} \left( j \right)}\).

\(c_{3}\left( j \right) \ \longrightarrow \ \ \frac{c_{3}\left( j \right)}{c_{1}\left( j \right)} \ ;\ \ c_{4}\left( j \right) \longrightarrow \ \ \frac{c_{4}\left( j \right)}{c_{1}\left( j \right)}\)

\(c_{5}\left( j \right) \ \longrightarrow \ \ \frac{c_{5}\left( j \right)}{c_{1}\left( j \right)} \ ;\ \ c_{6}\left( j \right) \longrightarrow \ \ \frac{c_{6}\left( j \right)}{c_{1}\left( j \right)}\)

\(c_{5}\left( j \right) \ \longrightarrow \ \ \frac{c_{5}\left( j \right)}{c_{1}\left( j \right)} \ ;\ \ c_{6}\left( j \right) \longrightarrow \ \ \frac{c_{6}\left( j \right)}{c_{1}\left( j \right)}\)

\(f_{1}\left( j \right) \ \longrightarrow \ \ f_{1}\left( j \right) \ - f_{3}\left( j \right) C_{4}\left( j \right)\)

\(f_{8}\left( j \right) \ \longrightarrow \ \ f_{8}\left( j \right) \ - f_{3}\left( j \right) C_{3}\left( j \right)\)

\(f_{5}\left( j \right) \ \longrightarrow \ \ f_{5}\left( j \right) \ - f_{3}\left( j \right) C_{5}\left( j \right)\)

\(f_{6}\left( j \right) \ \longrightarrow \ \ f_{6}\left( j \right) \ - f_{3}\left( j \right) C_{6}\left( j \right)\)

\(f_{3}\left( j \right) \ \longrightarrow \ \ 0\)

\(e_{1}\left( j + 1 \right) \ \longrightarrow \ \ e_{1}\left( j + 1 \right) \ - e_{4}\left( j + 1 \right) c_{3}\left( j \right)\)

\(e_{9}\left( j + 1 \right) \ \longrightarrow \ \ e_{9}\left( j + 1 \right) \ - e_{4}\left( j + 1 \right) c_{4}\left( j \right)\)

\(e_{10}\left( j + 1 \right) \ \longrightarrow \ \ e_{10}\left( j + 1 \right) \ - e_{4}\left( j + 1 \right) c_{5}\left( j \right)\)

\(e_{8}\left( j + 1 \right) \ \longrightarrow \ \ e_{8}\left( j + 1 \right) \ - e_{4}\left( j + 1 \right) c_{6}\left( j \right)\)

\(e_{4}\left( j + 1 \right) \ \longrightarrow \ 0\)

\(f_{1}\left( j + 1 \right) \ \longrightarrow \ \ f_{1}\left( j + 1 \right) \ - f_{2}\left( j + 1 \right) c_{5}\left( j \right)\)

\(f_{4}\left( j + 1 \right) \ \longrightarrow \ \ f_{4}\left( j + 1 \right) \ - f_{2}\left( j + 1 \right) c_{4}\left( j \right)\)

\(f_{7}\left( j + 1 \right) \ \longrightarrow \ \ f_{7}\left( j + 1 \right) \ - f_{2}\left( j + 1 \right) c_{3}\left( j \right)\)

\(f_{6}\left( j + 1 \right) \ \longrightarrow \ \ f_{6}\left( j + 1 \right) \ - f_{2}\left( j + 1 \right) c_{6}\left( j \right)\)

\(f_{2}\left( j + 1 \right) \ \longrightarrow \ \ 0\)

8. Multiply non-zero coefficients in Eq. (5.4-40) by \(\frac{1}{f_{1} \left( j \right)}\).

\(f_{5}\left( j \right) \ \longrightarrow \ \ \frac{f_{5}\left( j \right)}{f_{1}\left( j \right)} \ ;\ \ f_{6}\left( j \right) \longrightarrow \ \ \frac{f_{6}\left( j \right)}{f_{1}\left( j \right)} ;\)

\(f_{8}\left( j \right) \ \longrightarrow \ \ \frac{f_{8}\left( j \right)}{f_{1}\left( j \right)} \ ;\ \ f_{1}\left( j \right) \longrightarrow \ 1\)

\(e_{1}\left( j + 1 \right) \ \longrightarrow \ \ e_{1}\left( j + 1 \right) \ - e_{9}\left( j + 1 \right) f_{5}\left( j \right)\)

\(e_{10}\left( j + 1 \right) \ \longrightarrow \ \ e_{10}\left( j + 1 \right) \ - e_{9}\left( j + 1 \right) f_{5}\left( j \right)\)

\(e_{8}\left( j + 1 \right) \ \longrightarrow \ \ e_{8}\left( j + 1 \right) \ - e_{9}\left( j + 1 \right) f_{6}\left( j \right)\)

\(e_{9}\left( j + 1 \right) \ \longrightarrow \ 0\)

\(f_{1}\left( j + 1 \right) \ \longrightarrow \ \ f_{1}\left( j + 1 \right) \ - f_{4}\left( j + 1 \right) f_{5}\left( j \right)\)

\(f_{7}\left( j + 1 \right) \ \longrightarrow \ \ f_{7}\left( j + 1 \right) \ - f_{4}\left( j + 1 \right) f_{8}\left( j \right)\)

\(f_{6}\left( j + 1 \right) \ \longrightarrow \ \ f_{6}\left( j + 1 \right) \ - f_{4}\left( j + 1 \right) f_{6}\left( j \right)\)

\(f_{4}\left( j + 1 \right) \ \longrightarrow \ \ 0\)

10. Set \(j\ \ \longrightarrow \ \ j + 1\)

11. If \(j < \text{JMAX}\), go to step 2

12. Multiply the non-zero coefficients in Eq. (5.4-40) by \(\frac{1}{f_{1} \left( j \right)}\)

\(f_{6}\left( j \right) \ \longrightarrow \ \ \frac{f_{6}\left( j \right)}{f_{1}\left( j \right)} \ ;\ \ f_{7}\left( j \right) \longrightarrow \ \ \frac{f_{7}\left( j \right)}{f_{1}\left( j \right)} ;\ \ f_{1} \left( j \right) \longrightarrow \ 1\)

\(e_{1}\left( j \right) \ \longrightarrow \ \ e_{1}\left( j \right) \ - e_{10}\left( j \right) f_{7}\left( j \right)\)

\(e_{8}\left( j \right) \ \longrightarrow \ \ e_{8}\left( j \right) \ - e_{10}\left( j \right) f_{6}\left( j \right)\)

\(e_{10}\left( j \right) \ \longrightarrow \ \ 0\)

\(e_{8}\left( j \right) \ \longrightarrow \ \ \frac{e_{8}\left( j \right)}{e_{1}\left( j \right)} \ ;\ \ e_{1}\left( j \right) \longrightarrow \ 1\)

\(\Delta T_{\text{CP}}\left( j \right) = e_{8}\left( j \right)\)

\(\Delta T_{\text{CT}}\left( j \right) = f_{6}\left( j \right) - f_{7}\left( j \right)\Delta T_{\text{CS}}\left( j \right)\)

16. Set \(j\ \ \longrightarrow \ \ j - 1\)

17. If \(j < 1\), go to step 23

\(\Delta T_{\text{CT}}\left( j \right) = f_{6}\left( j \right) - f_{5}\left( j \right)\Delta T_{\text{CT}}\left( j + 1 \right) - f_{8}\left( j \right)\Delta T_{\text{CS}}\left( j + 1 \right)\)

\(\Delta T_{\text{TU}}\left( j \right) = C_{6}\left( j \right) - C_{3}\left( j \right)\Delta T_{\text{CS}}\left( j + 1 \right) - C_{4}\left( j \right)\Delta T_{\text{CS}}\left( j + 1 \right) - C_{5}\left( j \right)\Delta T_{\text{CT}}\left( j + 1 \right)\)

\(\Delta T_{\text{CS}}\left( j \right) = e_{8}\left( j \right) - e_{5}\left( j \right)\Delta T_{\text{TU}}\left( j \right) - e_{7}\left( j \right)\Delta T_{\text{CS}}\left( j + 1 \right) - e_{10}\left( j \right)\Delta T_{\text{CT}}\left( j \right)\)

\(\Delta T_{\text{SH}}\left( j \right) = a_{4}\left( j \right) - a_{2}\left( j \right)\Delta T_{\text{CS}}\left( j \right) - a_{3}\left( j \right)\Delta T_{\text{CS}}\left( j + 1 \right)\)

22. Go to step 16

23. End

5.16.3. Appendix 5.3: Cover Gas Flow and Pressure Algorithm

The main steps in the cover gas treatment in Section 5.7 may be summarized in the following algorithm:

1. Initialize. Set \(I_{\text{n}} = 0\).

2. Start a loop on \(I_{\text{o}}\) for \(I_{\text{o}}\) = \(\text{ICV}1\), …, \(\text{ICV}2\). Set up \(\text{INEW} \left( I_{\text{o}} \right)\), \(\text{IOLD} \left( I_{\text{n}} \right)\), where \(I_{\text{o}}\) is the old compressible volume number and \(I_{\text{n}}\) is the new compressible volume number for the compressed arrays.

3. Is there gas in this compressible volume? Is \(\text{ITYPCV} \left( I_{\text{o}} \right)\) = 2,3,4,5, or 8? If so, go to step 5.

4. No gas in this compressible volume. \(\text{INEW} \left( I_{\text{o}} \right) = 0\),

\(p_{4} \left( I_{\text{o}} \right) = p_{3} \left( I_{\text{o}} \right)\),

\(T_{4} \left( I_{\text{o}} \right) = T_{3} \left( I_{\text{o}} \right)\),

\(m_{4} \left( I_{\text{o}} \right) = 0\). Go to the end of the loop, step 6.

5. Gas in this compressible volume.

\(I_{\text{n}} = I_{\text{n}} + 1\)

\(\text{INEW} \left(I_{\text{o}} \right) = I_{\text{n}}\)

\(\text{IOLD} \left(I_{\text{n}} \right) = I_{\text{o}}\)

\({p'}_{3} \left( I_{\text{n}} \right) = p_{3} \left( I_{\text{o}} \right), {m'}_{3} \left( I_{\text{n}} \right) = m_{3} \left( I_{\text{o}} \right)\) ,

\({V'}_{3} \left( I_{\text{n}} \right) = V_{3} \left( I_{\text{o}} \right), {V'}_{4} \left( I_{\text{n}} \right) = V_{4} \left( I_{\text{o}} \right)\) ,

\(\tau' \left( I_{\text{n}} \right) = \tau \left( I_{\text{o}} \right)\)

6. End of loop on \(I_{\text{o}}\). Loop back to step 3 for the next value of \(I_{\text{o}}\).

7. \(I_{\text{nmax}} = I_{\text{n}}\)

8. Start a loop on \(I_{\text{n}}\) for \(I_{\text{n}}\) = 1, …, \(I_{\text{nmax}}\)

Compute the adiabatic expansion and heat flow, as well as a temporary array \(c \left( i \right)\) (see below).

9. Re-calculate \({p'}_{3} \left( I_{\text{o}} \right)\) giving.

\({p'}_{3} \left( I_{\text{n}} \right) = {p'}_{3} \left( I_{\text{n}} \right) \left\{ 1 - \gamma \left\lbrack \frac{{V'}_{4} \left( I_{\text{n}} \right) - {V'}_{3} \left( I_{\text{n}} \right)}{{V'}_{4} \left( I_{\text{n}} \right)} \right\rbrack \right\}\)

Calculate \({T'}_{3} \left( I_{\text{n}} \right)\).

Set \(c \left( I_{\text{n}} \right) = \frac{{p'}_{3} \left( I_{\text{n}} \right)\gamma \Delta t_{\text{s}}}{{m'}_{3} \left( I_{\text{n}} \right) {T'}_{3} \left( I_{\text{n}} \right)}\)

Also set \(c \left( I, J \right) = 0\), with \(c \left( I_{\text{n}}, I_{\text{n}} \right) = 0\),

and \(d \left( I_{\text{n}} \right) = 0\).

10. End of loop on \(I_{\text{n}}\). Loop back to step 9 for the next value of \(I_{\text{n}}\).

11. Is there more than one gas compressible volume? Is \(I_{\text{nmax}} > 1\)? If so, go to step 13.

12. Go to step 25.

13. Start loop on I for I = 1, …, \(I_{\text{nmax}}-1\).

Initialize \(e_{\text{ij}}\), \(F_{1\text{ij}}\), \(F_{2\text{ij}}\).

14. Start loop on \(J\) for \(J = I_{\text{n}} + 1\), …, \(I_{\text{nmax}}\)

15. Set \(c \left( I,J \right) = 0.0\), \(c \left( J,I \right) = 0.0\), \(F_{1} \left( I,J \right) = 0.0\),

\(F_{1} \left( J,I \right) = 0.0\), \(F_{2} \left( I,J \right) = 0.0\), \(F_{2} \left( J,I \right) = 0.0\)

16. End of loop on \(J\). Loop back to step 11 for additional values of \(J\).

17. End of loop on I. Loop back to step 14 for additional values of \(I\).

18. Are there any gas segments? Is \(\text{ISG} 1 > 0\)?

If not, go to step 25.

19. Start loop on \(I_{\text{s}}\) for \(I_{\text{s}}\) = \(\text{ISG}1\), …, \(\text{ISG}2\).

Compute gas flow between compressible volumes.

20. Find \(I_{\text{ni}}\) and \(I_{\text{no}}\), the inlet and outlet compressible volumes for gas segment \(I_{\text{s}}\).

\(I_{\text{ni}} = \text{INEW} \left( \text{JNODG} \left( 1,I_{\text{s}} \right) \right)\)

\(I_{\text{no}} = \text{INEW} \left( \text{JNODG} \left( 2,I_{\text{s}} \right) \right)\)

21. Iterate routine to obtain \({F'}_{\text{o}},\ {F'}_{1},\ {F'}_{2},\ T_{\text{ij}}\) (See remarks after Eq. 5.7-12).

\(F_{1} \left( I_{\text{ni}},I_{\text{no}} \right) = F_{1} \left( I_{\text{ni}},I_{\text{no}} \right) + {F'}_{1}\) \(F_{1} \left( I_{\text{no}},I_{\text{ni}} \right) = F_{1} \left( I_{\text{no}},I_{\text{ni}} \right) + {F'}_{1}\) \(F_{2} \left( I_{\text{ni}},I_{\text{no}} \right) = F_{2} \left( I_{\text{ni}},I_{\text{no}} \right) + {F'}_{2}\) \(F_{2} \left( I_{\text{no}},I_{\text{ni}} \right) = F_{2} \left( I_{\text{no}},I_{\text{nio}} \right) + {F'}_{2}\) \(c \left( I_{\text{no}},I_{no} \right) = c \left( I_{\text{no}},I_{\text{no}} \right) - e\left( I_{\text{no}} \right) T_{\text{ij}} {F'}_{1}\) \(c \left( I_{\text{no}},I_{\text{ni}} \right) = c \left( I_{\text{no}},I_{\text{ni}} \right) - e\left( I_{\text{no}} \right) T_{\text{ij}} {F'}_{1}\) \(c \left( I_{\text{ni}},I_{\text{ni}} \right) = c \left( I_{\text{ni}},I_{\text{ni}} \right) - e\left( I_{\text{ni}} \right) T_{\text{ij}} {F'}_{2}\) \(c \left( I_{\text{ni}},I_{\text{no}} \right) = c \left( I_{\text{ni}},I_{\text{no}} \right) - e\left( I_{\text{ni}} \right) T_{\text{ij}} {F'}_{2}\) \(d \left( I_{\text{no}} \right) = d \left( I_{\text{no}} \right) + e\left( I_{\text{no}} \right) T_{\text{ij}} {F'}_{0}\) \(d \left( I_{\text{ni}} \right) = d \left( I_{\text{ni}} \right) - e\left( I_{\text{ni}} \right) T_{\text{ij}} {F'}_{0}\) \(F_{\text{os}} \left( I_{\text{ni}} \right) = F_{\text{os}} \left( I_{\text{no}} \right) + {F'}_{0}\) \(F_{\text{os}} \left( I_{\text{ni}} \right) = F_{\text{os}} \left( I_{\text{no}} \right) - {F'}_{0}\) \(F_{\text{os}} \left( I_{\text{s}} \right) = {F'}_{0}\) \(F_{\text{s}1} \left( I_{\text{s}} \right) = {F'}_{1}\) \(F_{\text{s}2} \left( I_{\text{s}} \right) = {F'}_{2}\)

23. End of loop on \(I_{\text{s}}\). Loop back to step 20 for the next value of \(I_{\text{s}}\).

24. Solve the matrix equation for \(\Delta p \left( i \right)\) (see Eq. 5.7-20).

25. Start loop on \(I_{\text{n}}\) for \(I_{\text{n}} = 1\), … \(I_{\text{nmax}}\)

\({p'}_{4}\left( I \right) = {p'}_{3}\left( I \right) + \Delta p_{\text{i}}\) \({m'}_{4}\left( I \right) = {m'}_{3}\left( I \right) + \Delta t_{\text{x}} F_{\text{os}}\left( I \right)\)

27. End of loop on \(I_{\text{n}}\). Loop back to step 26 for additional values of \(I_{\text{n}}\).

28. If \(I_{\text{nmax}} = 1\), go to step 34.

29. Start loop on \(I\) for \(I\) = 1, …, \(I_{\text{nmax}}-1\).

30. Start loop on \(J\) for \(J\) = \(I + 1\), \(I_{\text{nmax}}\).

\({m'}_{4} \left( I \right) = {m'}_{4} \left( I \right) + \Delta t_{\text{s}} \left\lbrack F_{1}\left( J,I \right)\Delta p\left( I \right) + F_{2}\left( J,I \right)\Delta p\left( J \right) \right\rbrack\) \({m'}_{4} \left( J \right) = {m'}_{4} \left( J \right) + \Delta t_{\text{s}} \left\lbrack F_{1}\left( I,J \right)\Delta p\left( J \right) + F_{2}\left( I,J \right)\Delta p\left( J \right) \right\rbrack\)

32. End of loop on \(J\). Loop back to step 31 for additional values of \(J\).

33. End of loop on \(I\). Loop back to step 30 for additional values of \(I\).

34. For \(I = 1\), …, \(I_{\text{nmax}}\) set

\({T'}_{4} \left( I \right) = \frac{{p'}_{4} \left( I \right) {V'}_{4} \left( I \right)}{{n'}_{4} \left( I \right)R}\)

35. Start loop on \(I_{\text{n}}\) for \(I_{\text{n}} = 1\), …, \(I_{\text{nmax}}\)

\(I_{o} = \text{IOLD}\left( I_{n} \right)\)

\(p_{3}\left( I_{o} \right) = {p'}_{3} \left( I_{n} \right)\)

\(m_{3}\left( I_{o} \right) = {m'}_{3} \left( I_{n} \right)\)

\(T_{3}\left( I_{o} \right) = {T'}_{3} \left( I_{n} \right)\)

37. End of loop on \(I_{\text{n}}\). Loop back to step 36 for additional values of \(I_{\text{o}}\).

38. If \(\text{ISG}1 = 0\), go to step 40.

39. For \(I_{\text{s}} = \text{ISG}1\), …, \(\text{ISG}2\)

\(I_{1} = \text{INEW}\left( \text{JNODG}\left( 1,I_{\text{s}} \right) \right)\)

\(I_{2} = \text{INEW}\left( \text{JNODG}\left( 2,I_{\text{s}} \right) \right)\)

\(F_{\text{g}4}\left( I_{\text{s}} \right) = F_{\text{so}}\left( I_{\text{s}} \right) + F_{\text{s}1}\left( I_{\text{s}} \right)\Delta p\left( I_{2} \right) = F_{\text{s}2}\left( I_{\text{s}} \right)\Delta p\left( I_{1} \right)\)

40. Optional debugging print-out.

41. Return

5.16.4. Appendix 5.4: Air Blast Heat Exchanger Stack Momentum Equation

This appendix derives an expression for the air mass flowrate through the natural convection stack. The stack contains an opening at its base through which air is drawn in, the air passes over the finned tubes of the air blast heat exchanger and then rises to be exhausted at the top of the stack.

The one-dimensional steady-state momentum equation for flow in a channel of uniform cross section is

(A5.4‑1)

\[\frac{\text{dP}}{\text{dz}} = \frac{- \text{d}}{\text{dz}} \left( \rho v^{2} \right) - \rho g \sin{\theta} - \tau \frac{P_{\text{w}}}{A}~ ,\]

where

\(p\) =pressure

\(\rho\) =density

\(v\) =velocity

\(\tau\) =wall shear stress

\(P_{\text{w}}\) =wetted perimeter

\(A\) =flow area

\(\theta\) =channel inclination relative to horizontal

Integrating Eq. A5.4-1 gives the pressure change along the channel

(A5.4‑2)

\[\Delta P = - \left( \frac{w}{A} \right)^{2} \left( \frac{1}{\rho_{\text{o}}} - \frac{1}{\rho_{\text{i}}} \right) - \rho_{\text{m}}g\mathcal{l} \sin{\theta} - \frac{K}{2\rho_{\text{m}}} \left( \frac{w}{a} \right)^{2}\]

where

\(w\) =channel mass flowrate

\(\mathcal{l}\) =channel length

\(\rho_{\text{o}}\) =outlet density

\(\rho_{\text{i}}\) =inlet density

\(\rho_{\text{m}}\) =mean density

\(K\) =flow loss coefficient

Using Eq. A5.4-2, the pressure change form stack inlet to above the heat exchanger is

(A5.4‑3)

\[\Delta P = - \left( \frac{w}{A_{\text{R}}} \right)^{2} \left\lbrack \frac{K_{\text{SI}}}{2\rho_{\text{c}}}\left( \frac{A_{\text{R}}}{A_{\text{SI}}} \right)^{2} + \frac{K_{\text{HX}}}{2\rho_{\text{c}}}\left( \frac{A_{\text{R}}}{A_{\text{HX}}} \right)^{2} \right\rbrack\]

where

\(A_{\text{SI}}\) = stack inlet cross-sectional area

\(A_{\text{R}}\) = riser cross-sectional area

\(A_{\text{HX}}\) = flow area at heat exchanger

\(K_{\text{SI}}\) = stack inlet loss coefficient

\(K_{\text{HX}}\) = heat exchanger loss coefficient

\(\rho_{\text{c}}\) =inlet air density

The gravity and acceleration terms have been neglected.

Similarly, the pressure change from the start of the riser to the stack outlet is

(A5.4‑4)

\[\Delta P = - \left( \frac{w}{A_{\text{R}}} \right)^{2} \frac{\left( K_{\text{SO}} + K_{\text{R}} \right)}{2\rho_{\text{h}}} - \rho_{\text{h}} g\mathcal{l}\]

where

\(K_{\text{SO}}\) = stack outlet loss coefficient

\(K_{\text{R}}\) = riser loss coefficient

\(\rho_{\text{h}}\) = riser air density

\(\mathcal{l}\) = riser length

The pressure change from the stack outlet through the outside air back to the stack inlet is approximately

(A5.4‑5)

\[\Delta P = \rho_{\text{c}} g \mathcal{l}\]

The above three pressure changes, Eqs. A5.4-3 through A5.4-5, must sum to zero since they are taken around a closed circuit. Solving for the air flowrate yields

(A5.4‑6)

\[w^{2} = \frac{\left( \rho_{\text{c} - \rho_{\text{h}} \right) g\mathcal{l} A_{\text{R}}^{2}}{\frac{K_{\text{SI}}}{2\rho_{\text{c}}} \left( \frac{A_{\text{R}}}{A_{\text{SI}}} \right)^{2} + \frac{K_{\text{HX}}}{2\rho_{\text{c}}} \left( \frac{A_{\text{R}}}{A_{\text{HX}}} \right)^{2} + \frac{\left( K_{\text{SO}} + K_{\text{R}} \right)}{2\rho_{\text{h}}}}\]

5.16.5. Appendix 5.5: Interpolation from User-Supplied Tables

A number of user-supplied tables are used in the SAS4A/SASSYS‑1 code. These tables are of the form \(Y \left( i \right)\) as a function of \(X \left( i \right)\). The default option is to use linear interpolation between points in the table to obtain \(Y\) as a function of \(X\). If \(X\) is between \(X \left( J \right)\) and \(X \left( J+1 \right)\), then linear interpolation gives

(A5.5‑1)

\[Y\left( X \right) = Y\left( J \right) + \frac{Z\left\lbrack Y \left( J + 1 \right) - Y\left( J \right) \right\rbrack}{\left\lbrack X \left( J + 1 \right) - X\left( J \right) \right\rbrack}\]

where

(A5.5‑2)

\[Z = X - X\left( J \right)\]

Linear interpolation has the advantages that it is simple to do and it never exhibits the wild behavior and spurious oscillations that higher order interpolation schemes can give. On the other hand, linear interpolation has some disadvantages. One disadvantage is that if only a few widely-spaced points are used for a table, linear interpolation may not be very accurate between points. Another disadvantage is that linear interpolation gives slope discontinuities at the table points. These slope discontinuities can cause corresponding slope discontinuities in plots of powers, temperatures, and flow rates calculated by the code. Sometimes these slope discontinuities correspond to real physical events, such as scramming the control rods or tripping the pumps; but usually they are numerical artifacts of the interpolation scheme. In order to address this problem, alternative interpolation schemes are available for some of the tables used by the code. Table 5.16.1 lists the interpolation options.

For the third order fit,

(A5.5‑3)

\[Y\left( X \right) = C_{1\text{J}} + C_{2\text{J}}Z + C_{3\text{J}}Z^{2} + C_{4\text{J}} Z^{3}\]

where the coefficients C are picked such that:

1. \(Y\) is continuous at \(X \left( J \right)\) and \(X \left( J+1 \right)\).

2. The slope of \(Y\) is continuous at internal points.

3. The value of \(F\) is minimized, where

(A5.5‑4)

\[F = \int_{\text{X}_{\text{min}}}^{\text{X}_{\text{max}}}{\left( \frac{\text{d}^2 \text{y}}{\text{dx}^2} \right)^2 \text{dx}}\]

Table 5.16.1 Table Interpolation Options for a Table of \(Y \left( i \right)\) vs. \(X \left( i \right)\), as Determined by the User-Specified Parameter IFIT

\(\text{IFIT} \left( K \right) = 0\)	Use linear fits
1	3rd order fits
2	3rd order fits with slope discontinuities at points where \(X \left( i+1 \right) - X \left( i \right) < .001\)
3	Linear fit to \(\log{\left( Y \right)}\)
4	3rd order fit to \(\log{\left( Y \right)}\)
5	3rd order fit to \(\log{\left( Y \right)}\) with slope discontinuities
\(K = 1\)	Power vs time or user specified reactivity vs time
2	PRIMAR-1 pump head vs time or channel flow vs time
3	PRIMAR-1 inlet temperature vs time
4	PRIMAR-4 pump head, motor torque, or pump speed vs time

Note: For all other tables, linear interpolation is used.

In this equation \(X_{\text{min}}\) and \(X_{\text{max}}\) are the first and last points in the table if IFIT = 1 or 4. If IFIT = 2 or 5, then the table is broken up into ranges, with the boundaries between ranges occurring at the points where the slope discontinuities occur. In this case, the fitting is done separately for each range; and \(X_{\text{min}}\) and \(X_{\text{max}}\) are the points at the ends of the range. There are some special cases or exceptions:

1. For all fitting options, if \(X\) is less than the first entry in the table, then \(Y\) is set equal to the first value of \(Y\) in the table. Also, if \(X\) is greater than the last entry in the table, then the last value of \(Y\) is used.

2. For IFIT = 2 or 5, in an interval where a slope discontinuity occurs \(\left( X \left( i+1 \right) - X \left( i \right) < .001 \right)\) linear interpolation is used from \(X \left( i \right)\) to \(X \left( i+1 \right)\).

3. If there are only two points in a range, then linear interpolation is used.

4. For IFIT = 1, 2, 4 or 5, if there are only 3 points in a range, then a parabola is fitted to the 3 points to determine the values of C in the range. Third order fits are only used if there are at least 4 points in a range.

Care should be taken when using third order fits, since they can result in spurious wiggles. Figure 5.16.1 shows the results of a third order fit to the power level in the SHRT-17 test in EBR-II. In this case, the third order fit to the power produces wiggles, whereas the third order fit to the logarithm of the power produces a smooth curve.

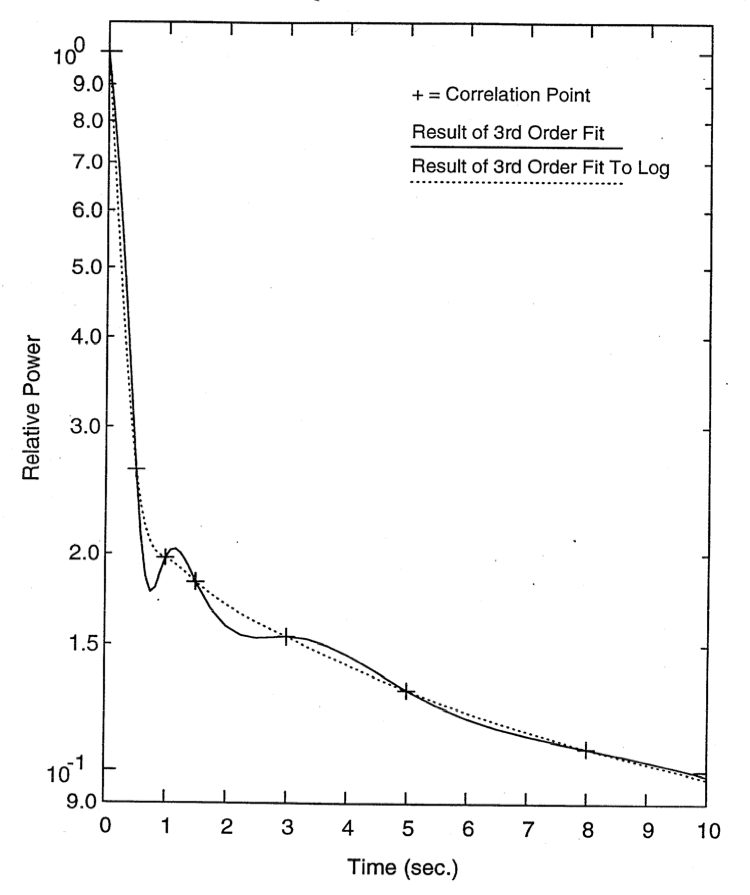
Figure 5.16.1 Figure A5.5-1. Fit to SHRT-17 Normalized Total Power, Early Times.

5.16.6. Appendix 5.6: Optional Eulerian Solution for Pipe Temperatures

As mentioned in Section 5.4.1, a Eulerian calculation can be used to speed up the pipe temperature calculation if the coolant moves more than two nodes in a time step. This Eulerian speed-up has only been implemented for flow in the nominal direction; if flow reversal has occurred in a pipe, then the Eulerian calculation is not used.

For the Eulerian calculation, Eq. (5.4-1) for the coolant is replaced by

(A5.6‑1)

\[\rho_{\text{c}} c_{\text{c}}A_{\text{c}} \frac{\partial \text{T}_{\text{c}}}{\partial \text{t}} + wc_{\text{c}} \frac{\partial \text{T}_{\text{c}}}{\partial \text{z}} = P_{\text{er}} h_{\text{wc} }\left( T_{\text{w}} - T_{\text{c}} \right)\]

Eq. (5.4-2) is still used for the wall. Finite differencing of Eq. A5.6-1 gives

(A5.6‑2)

\[\begin{split} \rho_{\text{c}} c_{\text{c}}A_{\text{c}}\left\lbrack \frac{T_{\text{c}6\text{j}} + T_{\text{c}6\text{j} + 1} - T_{\text{c}5\text{j}} - T_{\text{c}5\text{j}}}{2\delta t} \right\rbrack \\ + \frac{wc_{\text{c}}}{\delta t} \left\lbrack \theta_{1} \left( T_{\text{c}5\text{j} + 1} - T_{\text{c}5\text{j}} \right) + \theta_{2}\left( T_{\text{c}6\text{j} + 1} - T_{\text{c}6\text{j}} \right) \right\rbrack = \\ P_{\text{er}} h_{\text{wc}} \left\{ \theta_{1} \left\lbrack T_{\text{w}5\text{j}} - \frac{T_{\text{c}5\text{j}} + T_{\text{c}5\text{j} + 1}}{2} \right\rbrack \\ + \theta_{2} \left\lbrack T_{\text{w}6\text{j}} - \frac{T_{\text{c}6\text{j}} + T_{\text{c}6\text{j} + 1}}{2} \right\rbrack \right\}\end{split}\]

Similarly, finite differencing of Eq. (5.4-2) gives

(A5.6‑3)

\[\begin{split} \frac{M_{\text{w}} C_{\text{w}}}{\delta t} \left( T_{\text{w}6\text{j}} - T_{\text{w}5\text{j}} \right) = P_{\text{er}} h_{\text{wc}} \left\lbrack \theta_{1} \left( \frac{T_{\text{c}5\text{j}} + T_{\text{c}5\text{j} + 1}}{2} - T_{\text{w}5\text{j}} \right) \\ + \theta_{2} \left( \frac{T_{\text{c}6\text{j}} + T_{\text{c}6\text{j} + 1}}{2} - T_{\text{w}6\text{j}} \right) \right\rbrack \\ + \left( hA \right)_{\text{snk}} \left( T_{\text{snk}} - \theta_{1} T_{\text{w}5\text{j}} - \theta_{2} T_{\text{w}6\text{j}} \right)\end{split}\]

Eq. A5.6-3 can be rewritten as

(A5.6‑4)

\[T_{\text{w}6\text{j}} = B_{\text{w}0\text{j}} + B_{\text{w}1\text{j}} \left( T_{\text{c}6\text{j}} + T_{\text{c}6\text{j} + 1} \right)\]

where

(A5.6‑5)

\[B_{\text{w}1\text{j}} = \frac{P_{\text{er}} h_{\text{wc}} \theta_{2}\delta t}{2 d_{\text{w}}}\]

(A5.6‑6)

\[d_{\text{w}} = M_{\text{w}} C_{\text{w}} + \theta_{2} \delta t \left\lbrack P_{\text{er}} h_{\text{wc}} + \left( hA \right)_{\text{snk}} \right\rbrack\]

and

(A5.6‑7)

\[\begin{split} B_{\text{w}0\text{j}} = - \left\{ M_{\text{w}} C_{\text{w}} T_{\text{w}5\text{j}} + P_{\text{er}} h_{\text{wc}} \theta_{1} \delta t \left\lbrack \frac{T_{\text{c}5\text{j}} + T_{\text{c}5\text{j} + 1}}{2} - T_{\text{w}5\text{j}} \right\rbrack \\ + \left( hA \right)_{\text{snk}} \delta t \left( T_{\text{snk}} - \theta_{1} T_{\text{w}5\text{j}} \right) \right\} \big/ d_{\text{w}}\end{split}\]

Similarly, Eq. A5.6-2 can be rewritten as

(A5.6‑8)

\[T_{\text{c}6\text{j} + 1} = B_{\text{c}0\text{j}} + B_{\text{c}1\text{j}} T_{\text{c}6\text{j}} + B_{\text{c}2\text{j}} T_{\text{w}6\text{j}}\]

where

(A5.6‑9)

\[\begin{split} B_{\text{c}0\text{j}} = \left\{ \Delta z \rho_{\text{c}} c_{\text{c}} A_{\text{c}} + \left( T_{\text{c}5\text{j}} + T_{\text{ctj} + 1} \right) + 2\theta_{1} \delta t w c_{\text{c}} \left( T_{\text{c}5\text{j}} - T_{\text{c}5\text{j} + 1} \right) \\ + 2 \theta_{1} \delta t P_{\text{er}} h_{\text{wc}} \left\lbrack T_{\text{w}5\text{j}} - \frac{T_{\text{c}5\text{j}} + T_{\text{c}5\text{j} + 1}}{2} \right\rbrack \right\} \big/ d_{\text{c}}\end{split}\]

(A5.6‑10)

\[d_{\text{c}} = \rho_{\text{c}} c_{\text{c}} A_{\text{c}} \Delta z + 2\theta_{2} \text{dt} \left( wc_{\text{c}}\frac{P_{\text{er}} h_{\text{wc}}}{2} \Delta z \right)\]

(A5.6‑11)

\[B_{\text{c}1\text{j}} = - \left\{ \rho_{\text{c}} c_{\text{c}} A_{\text{c}} \Delta z + 2\theta_{2} \delta t \left( \frac{P_{\text{er}} h_{\text{wc}}}{2} \Delta z - wc_{\text{c}} \right) \right\} \big/ d_{\text{c}}\]

and

(A5.6‑12)

\[B_{\text{c}2\text{j}} = \frac{2\theta_{2} \delta t\Delta z P_{\text{er}} h_{\text{wc}}}{d_{\text{c}}}\]

Eqs. A5.6-4 and A5.6-8 can be combined to give

(A5.6‑13)

\[T_{\text{c}6\text{j} + 1} = B_{\text{cc}0\text{j}} + B_{\text{cc}1\text{j}} T_{\text{c}6\text{j}}\]

where

(A5.6‑14)

\[B_{\text{cc}0\text{j}} = \frac{B_{\text{c}0\text{j}} + B_{\text{c}2\text{j}} B_{\text{w}0\text{j}}}{1 - B_{\text{c}2\text{j}} B_{\text{w}1\text{j}}}\]

and

(A5.6‑15)

\[B_{\text{cc}1\text{j}} = \frac{B_{\text{c}1\text{j}} + B_{\text{c}2\text{j}} B_{\text{w}1\text{j}}}{1 - B_{\text{c}2\text{j}} B_{\text{w}1\text{j}}}\]

Note that \(B_{\text{cc}0\text{j}}\) and \(B_{\text{cc}1\text{j}}\) can be calculated before the temperatures at the end of the sub-interval are known.

The pipe inlet temperature at the end of the step is used to set the first coolant temperature, \(T_{\text{c}61}\). The code marches along the pipe, using Eq. A5.6-13 to calculate \(T_{\text{c}6\text{j}+1}\) after \(T_{\text{c}6\text{j}}\) has been calculated. After the coolant temperatures have been calculated, Eq. A5.6-4 is used to calculate the wall temperatures.