5.3. Specific Components: Contributions to Flow and Pressure Equations

In this section, we shall consider the contributions to the mass flow-rate and pressure equations from the various components in the primary and intermediate loops. Each compressible volume contributes a \(b_0\), a \(b_1\), and a \(b_2\) in Eq. 5.2-19, and each element in each segment connecting two compressible volumes contributes a \(\Delta a_0\), a \(\Delta a_1\), a \(\Delta a_2\), and a \(\Delta a_3\) in Eqs. 5.2-10, 5.2-12, 5.2-14, and 5.2-16. We shall consider compressible volumes without cover gas, compressible volumes with cover gas, pipes, intermediate heat exchangers, and pumps.

5.3.1. Compressible Volumes Without Cover Gas

A compressible volume with no cover gas is treated as a compressible liquid in an expandable container. The volume \(V\) is assumed to vary linearly with pressure p and temperature \(T\):

(5.3‑1)

\[V = V_{\text{r}} \left\lbrack 1 + \alpha_{\text{p}}\left( p - p_{\text{r}} \right) + \alpha_{\text{T}}\left( T - T_{\text{r}} \right) \right\rbrack\]

where \(V_{\text{r}}\) is the volume at a reference pressure \(p_{\text{r}}\) and reference temperature \(T_{\text{r}}\). Also the coolant density \(\rho\) is assumed to vary linearly with \(p\) and \(T\):

(5.3‑2)

\[\rho = \rho_{\text{r}} \left\lbrack 1 + \beta_{\text{p}}\left( p - p_{\text{r}} \right) + \beta_{\text{T}}\left( T - T_{\text{r}} \right) \right\rbrack\]

where

\(\alpha_{\text{p}}\) = the volume pressure expansion coefficient, \(\frac{1}{V} \frac{\partial \text{V}}{\partial \text{p}}\)

\(\alpha_{\text{T}}\) = the volume thermal expansion coefficient, \(\frac{1}{V} \frac{\partial \text{V}}{\partial \text{T}}\)

\(\beta_{\text{p}}\) = the sodium compressibility, \(\frac{1}{\rho} \frac{\partial \text{p}}{\partial \text{p}}\)

\(\beta_{\text{T}}\) = the sodium thermal expansion coefficient, \(\frac{1}{\rho} \frac{\partial \mathrm{\rho}}{\partial \text{T}}\)

The mass of the liquid in the compressible volume is

(5.3‑3)

\[m = \rho V\]

Using Eqs. 5.3-1 and 5.3-2 in Eq. 5.3-3 and dropping second-order terms gives

(5.3‑4)

\[m = m_{\text{r}} \left\lbrack 1 + \left( \alpha_{\text{p}} + \beta_{\text{p}} \right) \left( p - p_{\text{r}} \right) + \left( \alpha_{\text{T}} + \beta_{\text{T}} \right) \left( T - T_{\text{r}} \right) \right\rbrack\]

which can be rewritten as

(5.3‑5)

\[\delta p = \frac{\frac{\delta m}{m_{\text{r}}} - \left( \alpha_{\text{T}} + \beta_{\text{T}} \right) \delta T}{\alpha_{\text{p}} + \beta_{\text{p}}}\]

where

\(\delta m = m - m_{\text{r}}\)

\(\delta p = p - p_{\text{r}}\)

\(\delta T = T - T_{\text{r}}\)

Equation 5.3-5 is a general relationship for the pressure change in a compressible volume with no cover gas as a result of mass and temperature changes.

To obtain expressions for \(b_0 \left( j \right)\), \(b_1 \left( j \right)\), and \(b_2 \left( j \right)\), which characterize this compressible volume \(j\), we apply conservation of mass and conservation of energy principles to the volume with flow in and flow out during a time step. Conservation of mass gives

(5.3‑6)

\[\Delta m = \Delta t \left\lbrack \sum{{\overline{w}}_{\text{in}} - \sum{\overline{w}}_{\text{out}}} \right\rbrack\]

where \(\Delta m\) is the change in the liquid mass in the compressible volume during the time step \(\Delta t\), \(\sum{\overline{w}}_{\text{in}}\) is the sum of the average mass flow rates into the compressible volume during \(\Delta t\), and \(\sum{\overline{w}}_{\text{out}}\) is the sum of the average mass flow rates out during \(\Delta t\).

Conservation of energy gives

(5.3‑7)

\[\left( m_{3} + \Delta m \right) \left( T_{3} - \Delta T \right) = m_{3} T_{3} + \Delta t \left\lbrack \sum{{\overline{w}}_{\text{in}} T_{\text{in}} - \sum{{\overline{w}}_{\text{out}} T_{\text{out}}}} \right\rbrack + \frac{Q}{c_{\text{l}}} \Delta t\]

where \(m_3\) and \(T_3\) are the mass and temperature of the liquid in the compressible volume at the beginning of the time step, \(\Delta T\) is the change in temperature of the liquid in the compressible volume during the time step, \(\sum{\overline{w}}_{\text{in}}T_{\text{in}}\) in the sum of the average mass flow rates into the volume multiplied by the incoming temperature, \(\sum{{\overline{w}}_{\text{out}}T_{\text{out}}}\) is the sum of the average mass flow rates out of the volume multiplied by the outgoing temperature, \(Q\) is the heat flow rate from the compressible volume walls and from other components in contact with the compressible volume liquid, and \(c_{\text{l}}\) is the heat capacity of the liquid in the compressible volume. Equation 5.3-7 expresses the fact that the energy in the liquid in the compressible volume at the end of the time step is the sum of the energy present at the beginning of the time step, the excess of the energy flowing in over that flowing out during the time step, and the energy contributed to the liquid from the walls of the compressible volume during the time step.

Solving Eq. 5.3-7 for the change in the liquid temperature during the time step, gives

(5.3‑8)

\[\Delta T = \frac{- T_{3} \Delta m + \Delta t \left\lbrack \sum{{\overline{w}}_{\text{in}} T_{\text{in}} - \sum{{\overline{w}}_{\text{out}} T_{\text{out}}}} \right\rbrack + \frac{Q}{c_{\text{l}}} \Delta t}{m_{3} + \Delta m}\]

To first order, the \(m_3 + \Delta m\) in the denominator is approximated as \(m_3\). Inserting Eqs. 5.3-6 and 5.3-8 into Eq. 5.3-5 gives

(5.3‑9)

\[\begin{split}\Delta p = \left\lbrack \sum{{\overline{w}}_{\text{in}} - \sum{\overline{w}}_{\text{out}}} \right\rbrack \frac{\Delta t}{\alpha_{\text{p}} + \beta_{\text{p}}} \left\lbrack \frac{1}{m_{\text{r}}} + \frac{\left( \alpha_{\text{T}} + \beta_{\text{T}} \right) T_{3}}{m_{3}} \right\rbrack \\ - \frac{\left( \alpha_{\text{T}} + \beta_{\text{T}} \right) \Delta t}{\left( \alpha_{\text{p}} + \beta_{\text{p}} \right) m_{3}} \left\lbrack \sum{{\overline{w}}_{\text{m}} T_{\text{in}} - \sum{{\overline{w}}_{\text{out}} T_{\text{out}} + \frac{Q}{c_{\text{t}}}}} \right\rbrack\end{split}\]

Comparison of this equation with Eq. 5.2-19 shows that for the compressible volume with no cover gas

(5.3‑10)

\[b_{0} = - \frac{\left( \alpha_{\text{T}} + \beta_{\text{T}} \right) Q\Delta t}{\left( \alpha_{\text{p}} + \beta_{\text{p}} \right) m_{3} c_{\text{l}}}\]

(5.3‑11)

\[b_{1} = \frac{\Delta t}{\alpha_{\text{p}} + \beta_{\text{p}}} \left\lbrack \frac{1}{m_{\text{r}}} + \frac{\left( \alpha_{\text{T}} + \beta_{\text{T}} \right) T_{3}}{m_{3}} \right\rbrack\]

and

(5.3‑12)

\[b_{2} = - \frac{\left( \alpha_{\text{T}} + \beta_{\text{T}} \right) \Delta t}{\left( \alpha_{\text{p}} + \beta_{\text{p}} \right) m_{3}}\]

The \(Q \Delta t\) term in Eq. 5.3-10 is calculated in a manner similar to that described in Section 5.4.4, except that the value for \(b_0\) is calculated before the temperatures at the end of the step are calculated, so \(q\) is calculated on the basis of temperatures at the beginning of the time step. In the present version of the code, the reference mass \(m_{\text{r}}\) and the reference temperature \(T_{\text{r}}\) are taken as the mass and temperature at the beginning of the time step.

5.3.2. Compressible Volumes With Cover Gas

A compressible volume with cover gas is treated in a fashion similar to that without cover gas except that the compression of the liquid is neglected compared with the compression of the gas, so that all of the expansion or compression is attributed entirely to the gas. The cover gas is assumed to expand or compress adiabatically, and an increase in the gas volume is equal to the decrease in the liquid volume. The accompanying rise or fall in the level of the gas-liquid interface is taken as the volume change divided by the area of the compressible volume. In addition, the conservation of mass and the conservation of energy principles are observed. The conservation of mass is applied by taking the increase in the mass of the liquid in a compressible volume as the difference between the liquid flowing in and that flowing out during a time step, and the conservation of energy is taken as the increase in the mass of the liquid in the compressible volume times its temperature as the difference between the mass times temperature flowing in and that flowing out during a time step.

The liquid pressure at an elevation, \(z_{\text{r}}\), in the compressible volume is given by

(5.3‑13)

\[p_{\text{l}} = p_{\text{g}} + \rho_{\text{l}}g \left( z_{\text{i}} - z_{\text{r}} \right)\]

where

\(p_{\text{l}}\) = the pressure in the liquid

\(p_{\text{g}}\) = the pressure of the cover gas above the liquid

\(\rho_{\text{l}}\) = the liquid density

\(g\) = the acceleration of gravity

\(z_{\text{i}}\) = the height of the liquid gas interface

\(z_{\text{r}}\) = the reference height for the compressible volume

and the change in the liquid pressure in the compressible volume is obtained by taking differentials of Eq. 5.3-13:

(5.3‑14)

\[\Delta p_{\text{l}} = \Delta p_{\text{g}} + g\left( z_{\text{i}} - z_{\text{r}} \right) \Delta\rho_{\text{l}} + \rho_{\text{l}} g \Delta z_{\text{i}}\]

Adiabatic compression of the cover gas is taken as

(5.3‑15)

\[p_{\text{g}} V_{\text{g}}^{\gamma} = \text{const}\]

where

\(V_{\text{g}}\) = the volume of the cover gas

\(\gamma\) = the ratio of the specific heat at constant pressure to that at constant volume for the cover gas

and in differential form becomes:

(5.3‑16)

\[\frac{\Delta p_{\text{g}}}{p_{\text{g}}} + \gamma \frac{\Delta V_{\text{g}}}{V_{\text{g}}} = 0\]

The conservation of liquid mass for a compressible volume gives

(5.3‑17)

\[\Delta m_{\text{l}} = \Delta t \left\lbrack \sum{{\overline{w}}_{\text{in}} - \sum{\overline{w}}_{\text{out}}} \right\rbrack\]

where

\(\Delta m_{\text{l}}\) = the liquid mass increase in the compressible volume during the time step

\(\Delta t\) = the time-step size

\(\sum{\overline{w}}_{\text{in}}\) = the sum of the average liquid mass flow rates into the compressible volumes during the time step

\(\sum{\overline{w}}_{\text{out}}\) = the sum of the average liquid mass flow rates out from the compressible volume during the time step.

The conservation of energy for a compressible volume yields

(5.3‑18)

\[\left( m_{\text{l}} + \Delta m_{\text{l}} \right) \left( T_{\text{l}} + \Delta T_{\text{l}} \right) = m_{\text{l}} T_{\text{l}} + \Delta t \left\lbrack \sum{{\overline{w}}_{\text{in}} T_{\text{in}} - \sum{{\overline{w}}_{\text{out}} T_{\text{out}} }} \right\rbrack\]

where

\(m_{\text{l}}\) = the liquid mass at the beginning of the time step

\(\Delta T_{\text{l}}\) = the increase in liquid temperature in the compressible volume during the time step

\(\sum{{\overline{w}}_{\text{in}} T_{\text{in}}}\) = the sum of the average liquid mass flow rates times temperatures entering the compressible volume during the time step

\(\sum{\overline{w}}_{\text{out}} T_{\text{out}}\) = sum of the average liquid mass flow rates times temperatures leaving the compressible volume during the time step.

In the present version of the code, \(\Delta m_{\text{l}}\) is neglected in comparison with \(m\), giving

(5.3‑19)

\[\Delta T_{\text{l}} = \frac{\Delta t}{m_{\text{l}}} \left\lbrack \sum{{\overline{w}}_{\text{in}} T_{\text{in}} - \sum{{\overline{w}}_{\text{out}} T_{\text{out}}}} \right\rbrack\]

In addition to the above equations, we take

(5.3‑20)

\[\Delta V_{\text{g}} = - \Delta V_{\text{l}}\]

(5.3‑21)

\[V_{\text{l}} = \frac{m_{\text{l}}}{\rho_{\text{l}}}\]

(5.3‑22)

\[\Delta z_{\text{i}} = \frac{\Delta V_{\text{l}}}{A}\]

where

\(V_{\text{l}}\) = the volume of the liquid in the compressible volume at the beginning of a time step

\(m_{\text{l}}\) = the mass of the liquid in the compressible volume at the beginning of a time step

\(\rho_{\text{l}}\) = the density of the liquid

\(A\) = the area of the compressible volume.

Differencing Eq. 5.3-21, we have

(5.3‑23)

\[\Delta V_{\text{l}} = \frac{\Delta m_{\text{l}}}{\rho _{\text{l}}} - \frac{m_{\text{l}}}{\rho_{\text{l}}^{2}} \Delta \rho_{\text{l}}\]

and taking

(5.3‑24)

\[\Delta \rho_{\text{l}} = \frac{\partial \mathrm{\rho}}{\partial \text{T}} \Delta T_{\text{l}}\]

we can write the following expression for the change in the liquid pressure during a time step as

(5.3‑25)

\[\Delta p_{\text{l}} = \left( \gamma \frac{p_{\text{g}}}{V_{\text{g}}} + \frac{\rho_{\text{l}}g}{A} \right) \left( \frac{\Delta m_{\text{l}}}{\rho _{\text{l}}} - \frac{m_{\text{l}}}{\rho _{\text{l}}^{2}} \frac{\partial\rho}{\partial \text{T}} \Delta T_{\text{l}} \right) + g\left( z_{\text{i}} - z_{\text{r}} \right) \frac{\partial\rho}{\partial \text{T}} \Delta T_{\text{l}}\]

Inserting Eq. 5.3-17 for \(\Delta m_{\text{l}}\)and Eq. 5.3-19 for \(\Delta T_{\text{l}}\) and then comparing with Eq. 5.2-19, we see that the values of the \(b\)’s for a compressible volume with a cover gas are

(5.3‑26)

\[b_{0} = 0\]

(5.3‑27)

\[b_{1} = \Delta t \left[ \frac{\gamma P_{\text{g}}}{V_{\text{g}}\rho } + \frac{g}{a} \right]\]

(5.3‑28)

\[b_{2} = \Delta t \frac{\partial\rho}{\partial \text{T}} \left\lbrack \frac{g\left( z_{\text{i}} - z_{\text{r}} \right)}{m_{\text{l}}} - \frac{1}{\rho} \left( \frac{\gamma p_{\text{g}}}{V_{\text{g}}\rho} + \frac{g}{A} \right) \right\rbrack\]

5.3.3. Pipes and Intermediate Heat Exchangers

In considering the flow through a pipe or through an intermediate heat exchanger, several factors are taken into consideration. The contribution of the element to \(a_{\text{o}}\) in Eq. 5.2-9 is taken as

(5.3‑29)

\[\Delta a_{\text{o}} = L/A\]

where

\(L\) = the length of the element

\(A\) = the flow area of the element

The pressure drop contribution of the element to \(a_1\) in Eq. 5.2-11 is composed of a number of terms. One of these terms is the frictional pressure drop, which is written as

(5.3‑30)

\[\Delta p_{\text{fr}} = f \frac{L}{D_{\text{h}}} \frac{\rho v \left| v \right|}{2} = f \frac{L}{D_{\text{h}}} \frac{w \left| w \right|}{2 \rho A^{2}}\]

where

\(\Delta p_{\text{fr}}\) = the frictional pressure drop

\(f\) = the Moody friction factor

\(L\) = the length of the element

\(D_{\text{h}}\) = the hydraulic diameter of the element

\(\rho\) = the density of the liquid

\(v\) = the liquid velocity

\(w\) = the liquid mass flow rate

\(A\) = the flow area of the element

The Moody friction factor \(f\) for turbulent flow in pipes [5-2] is taken as

(5.3‑31)

\[f = C_{1} \left\lbrack 1 + \left( C_{2} \frac{\varepsilon}{D_{\text{h}}} + \frac{C_{3}}{\text{Re}} \right)^{C_{4}} \right\rbrack\]

where

\(C_1 = 0.0055\)

\(C_2 = 20,000\)

\(C_3 = 1.0 \times 10^{6}\)

\(C_4 = 1/3\)

\(\varepsilon\) = the user-supplied roughness of the element

\(\text{Re}\) = the Reynolds number

For laminar flow, the friction factor \(f\) is taken as

(5.3‑32)

\[f = 64/\text{Re}\]

The Reynolds number in either case is

(5.3‑33)

\[Re = \frac{D_{\text{h}} \left| w \right|}{A \mu}\]

where \(\mu\) is the viscosity of the fluid.

A second term is the pressure drop caused by bends in the flow path, and these are modeled as an additional frictional drop term, written as

(5.3‑34)

\[\Delta p = f \frac{L_{\text{B}}}{D_{\text{B}}} N_{\text{B}} \frac{w \left| w \right|}{2\rho A^{2}}\]

where

\(L_{\text{B}}/D_{\text{B}}\) = a user-supplied input number for an effective length-to-diameter ratio per bend

\(N_{\text{B}}\) =the number of bends in the element

A third term is the pressure drop, also proportional to the square of the mass flow rate, to account for baffles or restrictive orifices which cause greater pressure drops than would be accounted for by friction or bends above. This term is taken as

(5.3‑35)

\[\Delta p = G_{2} \frac{w \left| w \right|}{2\rho A^{2}}\]

where \(G_2\) is a user-supplied input number.

A fourth item is the second term in Eq. 5.2-1, which is proportional to the square of the mass flow rate, and is due to the difference in the fluid densities at the inlet and outlet ends of the element. It has the form

(5.3‑36)

\[\Delta p = \frac{w^{2}}{A^{2}} \left( \frac{1}{\rho_{O}} - \frac{1}{\rho_{I}} \right)\]

where

\(\rho_{\text{O}}\) = the fluid density at the element outlet

\(\rho_{\text{I}}\) = the fluid density at the element inlet

A final term is the gravity-head term for the element, taken as

(5.3‑37)

\[\Delta p = g\left( z_{\text{out}} - z_{\text{in}} \right) \overline{\rho}\]

where

\(z_{\text{out}}\) = the height of the element outlet

\(z_{\text{in}}\) = the height of the element inlet

\(g\) = the acceleration of gravity

\(\overline{\rho}\) = the average of the inlet and outlet fluid densities

Taking the above five terms together, the contribution from the element to \(a_1\) is

(5.3‑38)

\[\begin{split}\Delta a_{1} = - \Delta t \left\lbrack f \left( \frac{L}{D_{\text{h}}} + \frac{L_{\text{B}}}{D_{\text{B}}} N_{\text{B}} \right) \frac{w \left| w \right|}{2\rho A^{2}} + G_{2}\frac{w \left| w \right|}{2\rho A^{2}} \\ + \frac{w^{2}}{A^{2}} \left( \frac{1}{\rho_{O}} - \frac{1}{\rho_{\text{I}}} \right) + g \left( z_{\text{out}} - z_{\text{in}} \right) \overline{\rho} \right\rbrack\end{split}\]

The contribution of the element to \(a_2\), which is the derivative of the pressure drops with respect to time, as shown in Eq. 5.2-14, is zero, since the friction factors and the geometry are assumed not to change independently with time. Hence

(5.3‑39)

\[\Delta a_{2} = 0\]

The contribution of the element to \(a_3\), however, which is the derivative of the pressure drops with respect to the mass flow rate, as shown in Eq. 5.2-16, is obtained by differentiation. For laminar flow, differentiating Eq. 5.3-32 gives

(5.3‑40)

\[\frac{\partial \text{f}}{\partial \text{w}} = - \frac{f}{w}\]

For turbulent flow, differentiating Eq. 5.3-31 gives

(5.3‑41)

\[\frac{\partial \text{f}}{\partial \text{w}} = - \frac{C_{1}C_{3}C_{4}}{\text{Re} \left| w \right|} \left( C_{2} \frac{\varepsilon}{D_{\text{h}}} + \frac{C_{3}}{\text{Re}} \right)^{C_{4} - 1}\]

Taking the derivative with respect to \(w\) of each term in Eq. 5.3-38, we have for the contribution to \(a_3\)

(5.3‑42)

\[\begin{split}\Delta a_{3} = - \Delta t \left\{ \left( \frac{L}{D_{\text{h}}} + \frac{L_{\text{B}}}{D_{\text{B}}} N_{\text{B}} \right) \frac{1}{2\rho a^{2}} \left\lbrack 2f \left| w \right| + w \left| w \right| \frac{\partial \text{f}}{\partial \text{w}} \right\rbrack \\ + G_{2} \frac{ \left| w \right|}{\rho A^{2}} + 2w \left( \frac{1}{\rho_{O}} + \frac{1}{\rho_{I}} \right) \right\}\end{split}\]

5.3.4. Pumps

There are three pump choices available in the PRIMAR-4 module: a user-supplied table look-up, a centrifugal pump, and an electromagnetic pump. There are a number of options for the centrifugal and electromagnetic pumps.

5.3.4.1. Table Look-Up

The user supplies a table of relative pump head vs. time, and the code interpolates linearly between points in the table. The pump head as a function of time is given by

(5.3‑43)

\[H\left( t \right) = H_{\text{r}} f\left( t \right)\]

where \(f \left( t \right)\) is the user-supplied table, with \(f \left( t = 0 \right) = 1.0\), and \(H_{\text{r}}\) is the reference pump head for the particular pump. The contribution to the coefficients in Eqs. 5.2-10, 5.2-12, 5.2-14, and 5.2-16 are

(5.3‑44)

\[\Delta a_{0} = L/A\]

(5.3‑45)

\[\Delta a_{1} = \Delta t \left\lbrack H\left( t_{3} \right) - \text{GH} \right\rbrack\]

(5.3‑46)

\[\Delta a_{2} = \Delta t \left\lbrack H\left( t_{4} \right) - H \left( t_{3} \right) \right\rbrack\]

(5.3‑47)

\[\Delta a_{3} = 0\]

where

\(L\) = the length of the pump element

\(A\) = the element flow area

\(\Delta t\) = the time interval

\(t_3\), \(t_4\) = the times at the beginning and end of the time interval

\(\text{GH}\) = the gravity head for the pump element

5.3.4.2. Centrifugal Pumps

5.3.4.2.1. Option 1

In this option, the pump head and the pump torque are represented either by constant values or by polynomial fits, depending upon the pump flow rates or upon the pump speeds. The flow rates and speeds, and also the pump head and torque, are expressed as multiples of rated quantities, which are user-supplied. The constant values and the coefficients in the polynomial fits are also user-supplied.

The pump head and torque are expressed as functions of the parameter \(\chi\), which is

(5.3‑48)

\[\chi = \frac{\overline{w}}{\overline{s}}\]

with

(5.3‑49)

\[\overline{w} = \frac{w}{w_{\text{R}}}\]

(5.3‑50)

\[\overline{s} = \frac{s}{s_{\text{R}}}\]

where

\(w\) = the pump flow rate

\(w_{\text{R}}\) = the rated pump flow rate

\(s\) = the pump speed

\(s_{\text{R}}\) = the rated pump speed

Pump Head

For positive pump speeds the pump head is taken as

(5.3‑51)

\[ \begin{align} \Delta p_{\text{p}} = H_{\text{R}} s^{2} \left( A_{1} + A_{2} \chi + A_{3} \chi^{2} + A_{4} \chi^{3} + A_{5} \chi^{4} \right) , && \text{if } \chi < A_{6} \end{align}\]

(5.3‑52)

\[ \begin{align} \Delta p_{\text{p}} = H_{\text{R}} A_{7} {\overline{w}}^{2} , && \text{if } \left| \chi \right| > A_{6}\text{ and }\overline{w} \geq A_{18} \end{align}\]

(5.3‑53)

\[ \begin{align} \Delta p_{\text{p}} = - H_{\text{R}} A_{8} {\overline{w}}^{2} , && \text{if } \left| \chi \right| > A_{6}\text{ and }\overline{w} < - A_{18} \end{align}\]

(5.3‑54)

\[ \begin{align} \Delta p_{\text{p}} = H_{\text{R}} A_{7} \overline{w} A_{18} , && \text{if }\left| \chi \right| > A_{6} \text{ and } A_{18} > \overline{w} \geq 0 \end{align}\]

(5.3‑55)

\[ \begin{align} \Delta p_{\text{p}} = - H_{\text{R}} A_{8} \overline{w} A_{18} , && \text{if }\left| \chi \right| > A_{6} \text{ and } 0 > \overline{w} \geq - A_{18} \end{align}\]

where

\(\Delta p_{\text{p}}\) = the pump head

\(H_{\text{R}}\) = the reference pump head

\(A_1\) ,… \(A_8\) = user-supplied coefficients

For negative pump speeds, or flow reversal, the pump head is taken as

(5.3‑56)

\[\begin{split}\Delta p_{\text{p}} = \begin{cases} H_{R} A_{7} d_{1}^{2} & \text{if }d_{1} \geq 0 \\ H_{R} A_{8} d_{1}^{2} & \text{if }d_{1} < 0 \end{cases}\end{split}\]

with

\[d_{1} = \overline{w} - A_{10}\overline{s} ,\]

where

\(A_{10}\) = user-supplied coefficient

Pump Torque

Next, for positive pump speeds, the pump torque is

(5.3‑57)

\[ \begin{align} \overline{\tau} = {\overline{s}}^{2}\left( A_{11} + A_{12} \chi + A_{13}\chi^{2} + A_{14}\chi^{3} + A_{15}\chi^{4} \right), && \text{if } \left| \frac{\overline{w}}{\overline{s}} \right| \leq A_{6} \end{align}\]

(5.3‑58)

\[ \begin{align} \overline{\tau} = A_{16}{\overline{w}}^{2} , && \text{if } \left| \frac{\overline{w}}{\overline{s}} \right| > A_{6},\ \overline{w} \geq 0 \end{align}\]

(5.3‑59)

\[ \begin{align} \overline{\tau} = A_{17}{\overline{w}}^{2} , && \text{if } \left| \frac{\overline{w}}{\overline{s}} \right| > A_{6},\ \overline{w} < 0 \end{align}\]

with

(5.3‑60)

\[\overline{\tau} = \frac{\tau}{\tau_{\text{R}}}\]

where

\(\tau\) = the pump torque

\(\tau_{\text{R}}\) = the reference pump torque

\(\chi,\ \overline{w},\ \overline{s}\) = the same as for the pump head

\(A_{11}\), … \(A_{15}\) = user-supplied coefficient

For negative pump speeds, the pump torque is taken as

(5.3‑61)

\[ \begin{align} \overline{\tau} = A_{16}\left( \overline{w} - A_{20}\overline{s} \right)^{2} , && \text{if } \overline{w} \geq A_{20}\overline{s} \end{align}\]

(5.3‑62)

\[ \begin{align} \overline{\tau} = A_{17}\left( \overline{w} - A_{20}\overline{s} \right)^{2} , && \text{if } \overline{w} < A_{20}\overline{s} \end{align}\]

Pump Speed

The pump speed and pump torque are related by the equation is

(5.3‑63)

\[I \frac{\text{ds}}{\text{dt}} = \tau_{\text{m}} - \tau_{\text{p}} - k_{1} w\]

where

\(I\) = the moment of inertia of the pump and motor

\(s\) = the pump speed

\(\tau_{\text{m}}\) = the motor torque

\(\tau_{\text{p}}\) = the pump torque

\(k_1\) = constant of proportionality

\(w\) = the pump flow rate

The term \(- k_1\) w is a drag term proportional to the flow rate. The motor torque \(\tau_{\text{m}}\) is a user-supplied table look-up.

Rotor Lock-Up

If the normalized pump speed, \(\overline{s}\), falls below the value \(A_9\), and if \(A_9 > 0\), then the rotor locks; and the speed is held at zero after that.

Flow Rate Coefficients

The contribution to the \(a\)’s in Eqs. 5.2-10, 5.2-12, 5.2-14 and 5.2-16 are then as follows:

(5.3‑64)

\[\Delta a_{\text{o}} = L_{\text{p}}/A_{\text{p}}\]

(5.3‑65)

\[\Delta a_{1} = \Delta p_{\text{p}} - \rho_{\text{l}}g\left( z_{\text{in}} - z_{\text{out}} \right)\]

(5.3‑66)

\[\begin{split}\Delta a_{2} &= \left( \Delta t \right)^{2} \frac{\partial \Delta \text{p}_{\text{p}}}{\partial \text{t}} \\ &= \left( \Delta t \right)^{2} \frac{\partial \Delta \text{p}_{\text{p}}}{\partial \text{s}} \frac{\partial \text{s}}{\partial \text{t}}\end{split}\]

(5.3‑67)

\[\Delta a_{3} = \Delta t \frac{\partial}{\partial \text{w}} \Delta p_{\text{p}}\]

\(L_{\text{p}}\) = the length of the pump element

\(A_{\text{p}}\) = the flow area of the pump element

\(\Delta p_{\text{p}}\) = the pump head

\(\rho_{\text{l}}\) = the liquid density

\(g\) = the acceleration of gravity

\(z_{\text{in}}\) = the inlet elevation of the pump element

\(z_{\text{out}}\) = the outlet elevation of the pump element

\(\frac{\partial\mathrm{\Delta p_{\text{p}}}}{\partial \text{t}}, \frac{\partial \text{s}}{\partial \text{t}} \frac{\partial \mathrm{\Delta p_{\text{p}}}}{\partial \text{w}}\) = the partial derivatives of pump head and pump speed described above under the various conditions of speed and flow

5.3.4.2.2. Option 2

This pump option makes use of the homologous pump curves and should permit operation of the pump in all four quandrants of pump operations–normal pump mode, energy dissipation mode, turbine mode, and reverse pump mode. The actual curves used for the pump head and torque are, at present, built into the model using data statements and are the three-region curve fit taken from a memo by J. F. Koenig [5-1].

The pump head and torque values are obtained from

(5.3‑68)

\[H = H_{\text{r}} \left( {\overline{w}}^{2} + {\overline{s}}^{2} \right) \sum_{\text{i} = 0}^{6}{C_{\text{ji}} x^{i}}\]

(5.3‑69)

\[T = T_{\text{r}} \left( {\overline{w}}^{2} + {\overline{s}}^{2} \right) \sum_{\text{i} = 0}^{8}{D_{\text{ji}} x^{i}}\]

where

\(H\) = pump head

\(T\) = pump torque

\(w\) = flow rate

\(s\) = pump speed

\(x = \pi + \left( \frac{\overline{w}}{\overline{s}} \right) = \pi + \mathrm{atan2}\left( \overline{w},\overline{s} \right)\)

and the bar denotes normalization with respect to reference quantities\(\left( \text{i.e.}, \overline{w} = w/w_{\text{r}} \right)\) and the subscript \(r\) denotes reference quantities. The coefficients \(C_{\text{ji}}\) and \(D_{ji}\) represent the three-region curve fit with

\[\begin{split}j &= 1 , & 0 \leq x \leq 3.14159 \\ &= 2 , & 3.14159 \leq x \leq 4.7124 \\ &= 3 , & 4.7124 < x\end{split}\]

The value for \(H_{\text{r}}\) is an input while \(T_{\text{r}}\) is obtained from

(5.3‑70)

\[T_{\text{r}} = \frac{H_{\text{r}} w_{\text{r}}}{\left( s_{\text{r}} \eta \rho \right)}\]

where \(\eta\) is the pump efficiency at reference conditions and \(\rho\) is the fluid density.

At low flow conditions with \(\left| \overline{w} \right| < w_{\text{c}}\) where \(w_{\text{c}}\) represents a cutoff value specified by the user, the pump head is calculated as a linear interpolation between the pump head at zero flow and at the \(w_{\text{c}}\) flow:

(5.3‑71)

\[H \left( w,s \right) = \frac{\left( H \left( {\overline{w}}_{\text{c}},\overline{s} \right) \overline{w} + H\left( 0,\overline{s} \right) \left( w_{\text{c}} - \overline{w} \right) \right)}{w_{\text{c}}}\]

The value \(w_{\text{c}}\) is specified as an input value in APMPHD (13,IPMP) in input block 18. The frictional torque losses, \(T_{\text{f}}\), are taken as a three-region quadratic fit over \(\overline{s}\)

(5.3‑72)

\[T_{\text{f}} = T_{\text{r}} \left( A_{\text{j}1} + A_{\text{j}2} \overline{s} + A_{\text{j}3} \overline{s} \left| \overline{s} \right| \right)\]

where

\[\begin{split}\begin{matrix} j &= 1, &\overline{s} < s_{1} \\ &= 2, &s_{1} < \overline{s} s_{2} \\ &= 3, &s_{2} < \overline{s}~. \\ \end{matrix}\end{split}\]

The nine coefficients, \(A_{\text{ji}}\), are specified as input values in APMPHD (L,IPMP) in input block 18. The cutoff speeds \(s_1\) and \(s_2\) are also input values in APMPHD (L, IPMP).

For the steady-state, the subroutine SSPUMP makes use of a root finder to locate the pump speed necessary for a specified pump head. It is assumed that steady-state will be at a flow level above \(w_{\text{c}}\).

The subroutine PUMPFL includes the following calculations for \(\Delta a_{\text{o}}\), \(\Delta a_1\), \(\Delta a_2\) and \(\Delta a_3\), with

(5.3‑73)

\[\Delta a_{0} = L_{\text{K}}/A_{\text{K}}\]

(5.3‑74)

\[\Delta a_{1} = H_{g} + H\]

(5.3‑75)

\[\Delta a_{2} = \Delta t^{2} \frac{\partial}{\partial \text{t}}H\]

(5.3‑76)

\[\Delta a_{3} = \Delta t \frac{\partial}{\partial \text{w}}H\]

where \(L\), \(A\), \(H_{\text{g}}\), \(H\) and \(\Delta t\) represent the length, area, gravity head, pump head and time interval, respectively. The terms \(\Delta a_{\text{o}}\) and \(\Delta a_1\) are calculated as in the centrifugal pump option 1; \(\Delta a_2\) is found as follows:

(5.3‑77)

\[\Delta a_{2} = \Delta t^{2} \frac{\partial \overline{s}}{\partial \text{t}} \frac{\partial \text{H}}{\partial \text{s}}\]

where

(5.3‑78)

\[\frac{\partial \overline{\text{s}}}{\partial \text{t}} = \frac{\left( T_{\text{m}} - T_{\text{p}} - T_{\text{f}} \right)}{\left( s_{\text{r}}I \right)}\]

\(T_{\text{m}}\) = motor torque

\(I\) = pump inertia

and from Eqs. 5.3-67 and 5.3-70

(5.3‑79)

\[\frac{\partial \text{H}}{\partial \overline{\text{s}}} = 2H_{\text{r}} \overline{s} \sum_{\text{i} = 0}^{6}{c_{\text{ji}} x^{i}} - H_{\text{r}} \overline{w} \sum_{\text{i} = 1}^{6}{c_{\text{ji}} ix^{i - 1}}\]

for \(\left| \overline{w} \right| > w_{c}\text{and}\)

(5.3‑80)

\[\frac{\partial \text{H}}{\partial \overline{\text{s}}} = \frac{\left\lbrack \frac{\partial \text{H}}{\partial \overline{\text{s}}} \left( w_{\text{c}},\overline{s} \right) \overline{w} + \frac{\partial \text{H} \left( 0,\overline{s} \right)}{\partial \overline{\text{s}}} \left( w_{\text{c}} - \overline{w} \right) \right\rbrack}{w_{\text{c}}}\]

for \(\left| \overline{w} \right| < w_{\text{c}}~.\)

\(\Delta a_3\) is found using 5.3-76 and

(5.3‑81)

\[\begin{split}\frac{\partial \text{H}}{\partial \overline{w}} &= 2H_{\text{r}} \overline{w} \sum_{\text{i} = 0}^{6}{c_{\text{ji}}x^{i}} + H_{\text{r}}\overline{s}\sum_{\text{i} = 1}^{6}C_{\text{ji}} ix^{i - 1} \\ \frac{\partial \text{H}}{\partial \text{w}} &= \frac{1}{w_{\text{r}}} \frac{\partial \text{H}}{\partial \overline{\text{w}}}\end{split}\]

for \(\left| \overline{w} \right| > w_{\text{c}}\) and from

(5.3‑82)

\[\frac{\partial \text{H}}{\partial \overline{\text{w}}} = \frac{\left( H\left( w_{\text{c}},\overline{s} \right) - H\left( 0,\overline{s} \right) \right)}{w_{\text{c}}}\]

for \(\left| \overline{w} \right| < w_{\text{c}},\) and

The subroutine PUMPFN includes the pump torque curves in integrating Eq. 5.3-78 to determine \(s\). Approximating Eq. 5.3-78 as

(5.3‑83)

\[I \frac{\Delta s}{\Delta t} = T_{\text{m}} - \frac{1}{2} \left( T_{3} + T_{4} \right) - \frac{1}{2} \left( T_{\text{f}3} + T_{\text{f}4} \right)\]

Note where the subscripts 3 and 4 denote the beginning and ending times of the \(\Delta t\) interval and approximating

(5.3‑84)

\[T_{4} = T_{3} + \frac{\partial \text{T}}{\partial \text{s}} \Delta s + \frac{\partial \text{T}}{\partial \text{w}} \Delta w\]

(5.3‑85)

\[T_{\text{f}4} = T_{\text{f}3} + \frac{\partial \text{T}_{\text{f}}}{\partial \text{s}} \Delta s\]

in Eq. 5.3-83, \(\Delta s\) may be obtained as

(5.3‑86)

\[\Delta s = \frac{T_{\text{m}} - T_{3} - \frac{1}{2} \frac{\partial \text{T}}{\partial \text{w}} \Delta w - T_{f3}}{\left\lbrack \frac{I}{\Delta t} + \frac{1}{2} \frac{\partial \text{T}}{\partial \text{s}} + \frac{1}{2} \frac{\partial T_{\text{f}}}{\partial \text{s}} \right\rbrack}\]

Locked Rotor

If \(\overline{s} < A_{20}\), where \(A_{20}\) is the input variable APMPHD(20, IPMP), and if \(\overline{w} < A_{19}\), then the rotor locks and the pump speed is set to zero and held at zero. For a locked rotor the pump head is calculated as

(5.3‑86b)

\[\begin{split} H = \begin{cases} - T_{\text{r}} A_{12} w \left| w \right| \geq A_{13} & \text{if }\left| \overline{w} \right| \geq A_{13} \\ - T_{\text{r}} A_{12} A_{13} \overline{w} & \text{if }\left| \overline{w} \right| < A_{13} \end{cases}\end{split}\]

where \(A_{12}\) and \(A_{13}\) are input in the APMPHD(K, IPMP) array.

Pump Cavitation

In a centrifugal pump, cavitation will occur if the applied net positive suction head (ANPSH), or pump inlet pressure, is less than the required net positive suction head (RNPSH). This can occur if there is a break in the outlet pipe from the pump, leading to an increase in the pump flow rate and an increase in the RNPSH. If pump cavitation occurs, there will be a drop in pump head. Although there is reasonably good RNPSH data for many pumps, there is little data on pump behavior in the cavitation range, mainly because cavitation tends to destroy a pump, so no one wants to operate in that range. On the other hand, transient pump cavitation can occur for a short time after a pipe rupture, and the resulting decrease in pump head can have a significant impact on the flow out the rupture and on the flow rate through the core. The homologous pump model in PRIMAR-4 tests for pump cavitation and reduces the pump head if cavitation occurs.

The required net positive suction head is calculated as

(5.3‑87)

\[\text{RNPSH} = {\overline{s}}^{2} \left( C_{\text{c}0} + C_{\text{c}1} Z + C_{\text{c}2} Z^{2} + C_{\text{c}3} Z^{3} + C_{\text{c}4} Z^{4} \right)\]

where

(5.3‑88)

\[Z = \frac{\overline{w}}{\overline{s}}\]

Then, if RNPSH > ANPSH, the cavitated head, \(H_{\text{c}}\), is calculated as

(5.3‑89)

\[H_{\text{c}} = f_{\text{c}} H\]

where \(H\) is the normal head, calculated as described in the previous sections, and the cavitation factor \(f_{\text{c}}\) is calculated as

(5.3‑90)

\[f_{\text{c}} = \frac{1}{1 + 1000x^{2}}\]

where

(5.3‑91)

\[x = \frac{\text{RNPSH} - \text{ANPSH}}{\text{ANPSH}}\]

The cavitation factor of Eq. 5.3-90 is somewhat arbitrary; but, as previously mentioned, there is little data for behavior in the cavitation range, and this expression results in a rapid drop in pump head as the pump goes farther into the cavitation range. With this treatment, the expressions used in Eq. 5.3-76 and 5.3-77 for \(\Delta a_2\) and \(\Delta a_3\) are

(5.3‑92)

\[\frac{\partial \text{H}_{\text{c}}}{\partial \overline{\text{s}}} = f_{\text{c}} \left\lbrack \frac{\partial \text{H}}{\partial \overline{\text{s}}} - 2000 xH \frac{\partial \text{x}}{\partial \overline{\text{s}}} \right\rbrack\]

(5.3‑93)

\[\frac{\partial \text{H}_{\text{c}}}{\partial \overline{\text{w}}} = f_{\text{c}} \left\lbrack \frac{\partial \text{H}}{\partial \overline{\text{w}}} - 2000 xH \frac{\partial \text{x}}{\partial \overline{\text{w}}} \right\rbrack\]

5.3.4.2.3. EBR-II Pump Model

The third centrifugal pump option in PRIMAR-4 is essentially the pump model used in the NATDEMO code [5-5] for EBR-II. By adjusting the coefficients in the pump characteristics curves, this model could probably also be used for other reactors. This model is somewhat simpler than the option 2 model, in that the EBR-II pump model is mainly applicable to the first quadrant (positive flow, positive pump speed). This model can be used for negative flow, but it is probably not applicable to negative pump speed. Also, for the EBR-II pump model, the user specifies the pump speed as a function of time; whereas in options 1 and 2, the code calculated the pump speed.

In this option, the pump head is calculated from

(5.3‑94)

\[\overline{H} = b_{1} {\overline{s}}^{2} + b_{2} \overline{s} \overline{w} + b_{3} \frac{\overline{w}}{\left| \overline{w} \right|} \left| \overline{w} \right|^{b_{4}}\]

where

(5.3‑95)

\[\overline{H} = H/H_{\text{r}}\]

(5.3‑96)

\[\overline{s} = s/s_{\text{r}}\]

(5.3‑97)

\[\overline{w} = w/w_{\text{r}}\]

\(H\) = pump head

\(s\) = pump speed

and

\(w\) = coolant flow rate

The \(r\) subscript refers to the rated value. The coefficients \(b_1\) and \(b_2\) are constant, but the values of \(b_3\) and \(b_4\) depend on the speed and flow rate:

(5.3‑98a)

\[\begin{align} b_{3} = b_{3\text{m}} && \text{if }\overline{s} > \varepsilon_{\text{m}} \overline{w} \end{align}\]

(5.3‑98b)

\[\begin{align} b_{3} = b_{3\text{t}} && \text{if }\overline{s} \leq \varepsilon_{\text{m}} \overline{w} \text{ and } w \geq {\overline{w}}_{\text{t}} \end{align}\]

(5.3‑98c)

\[\begin{align} b_{3} = b_{3\text{l}} && \text{if }\overline{s} \leq \varepsilon_{\text{m}} \overline{w} \text{ and } w < {\overline{w}}_{\text{t}} \end{align}\]

(5.3‑99a)

\[\begin{align} b_{4} = b_{4\text{t}} && \text{if } \overline{s} > \varepsilon_{\text{m}} \overline{w} \text{ or } w \geq {\overline{w}}_{\text{t}} \end{align}\]

(5.3‑99b)

\[\begin{align} b_{4} = b_{4\text{l}} && \text{if } \overline{s} > \varepsilon_{\text{m}} \overline{w} \text{ or } w < {\overline{w}}_{\text{t}} \end{align}\]

Equations 5.3-98 and 5.3-99 are based on the idea of using a stopped-rotor pressure drop if \(\overline{s} < \varepsilon_{\text{m}} \overline{w}\). Also, the stopped-rotor pressure drop is a laminar value if \(\overline{w} < {\overline{w}}_{\text{t}}\), or a turbulent value if \(\overline{w} \geq {\overline{w}}_{\text{t}}\). The default values for the coefficients are:

(5.3‑100a)

\[b_{1} = 1.1740\]

(5.3‑100b)

\[b_{2} = .0818\]

(5.3‑100c)

\[b_{3\text{m}} = - .2558\]

(5.3‑100d)

\[b_{3\text{t}} = - .5923\]

(5.3‑100e)

\[b_{3\text{l}} = - .0471\]

(5.3‑100f)

\[b_{4\text{t}} = 1.9\]

(5.3‑100g)

\[b_{4\text{l}} = 1.0\]

(5.3‑100h)

\[{\overline{w}}_{\text{t}} = .06\]

(5.3‑100i)

\[\varepsilon_{\text{m}} = .55\]

(5.3‑100j)

\[H_{\text{r}} = 358,530 ~ \text{(Pa)}\]

(5.3‑100k)

\[w_{\text{r}} = 250.2 ~ \text{(kg/s)}\]

and

(5.3‑100l)

\[s_{r} = 14.5 ~ \text{revolutions/s} = 870 ~ \text{rpm}\]

This correlation produces a discontinuity in pump head at the switch from spinning rotor to stopped rotor. With the default values, the pump head is continuous at the transition from turbulent to laminar flow.

For the steady-state initialization in SSPUMP, the initial normalized pump head, \(\overline{H_{0}}\) and flow rate, \(\overline{w_{0}}\) , are known, and Eq. 5.3-94 is solved to find \(\overline{s_{0}}\), the initial steady-state pump speed:

(5.3‑101)

\[{\overline{s}}_{\text{o}} = \frac{- b_{2} {\overline{w}}_{0} + \left\lbrack b_{2}^{2} {\overline{w}}_{0}^{2} - 4b_{1} \left( b_{3} {\overline{w}}_{0}^{b_{4}} - {\overline{H}}_{0} \right) \right\rbrack^{1/2}}{2b_{1}}\]

It is assumed that \({\overline{s}}_{0} > \varepsilon_{\text{m}} {\overline{w}}_{0}\), and the values used for \(b_3\) and \(b_4\) in SSPUMP are \(b_{3\text{m}} b_{4\text{t}}\). The user supplies a table of normalized pump speed vs. time, normalized to the initial steady-state speed. The code then interpolates linearly from this table to get pump speeds for the transient calculation.

In PUMPFL where \(\Delta a_0\), \(\Delta a_1\), \(\Delta a_2\), and \(\Delta a_3\) are calculated, \(\Delta a_0\) and \(\Delta a_1\), are calculated using Eq. 5.3-64 and 5.3-65 or 5.3-73 and 5.3-74, as in the other pump options. For this option

(5.3‑102)

\[\Delta a_{2} = \Delta t^{2} \frac{\text{dH}}{\text{ds}} \frac{\text{ds}}{\text{dt}}\]

with

(5.3‑103)

\[\frac{\text{dH}}{\text{ds}} = \frac{\left( 2b_{1}\overline{s} + b_{2}\overline{w} \right) H_{\text{r}}}{S_{\text{r}}}\]

and \(ds/dt\) obtained from the user-specified table of normalized pump speed vs. time:

(5.3‑104)

\[\frac{\text{ds}}{\text{dt}} = \frac{s\left( t + \Delta t \right) - s\left( t \right)}{\Delta t}\]

also,

(5.3‑105)

\[\Delta a_{3} = \Delta t \frac{\text{dH}}{\text{dw}} = \Delta t\ H_{\text{r}} \left\lbrack b_{2} \overline{s} + b_{3} b_{4} \left( \frac{\overline{w}}{\left| w \right|} \right) \left| w \right|^{b_{4} - 1} \right\rbrack\]

5.3.4.2.4. Pump Head vs. Flow Option

One pump option in SAS4A/SASSYS‑1 allows the user to specify the normalized pump head as a function only of normalized flow rate. In this option, the normalization is to the initial steady-state values. The user supplies a table of normalized pump head vs. normalized flow rate, and the code uses linear interpolation between the entries in the table.

For this option, \(\Delta a_0\) and \(\Delta a_1\) for the pump are calculated in the same way as for the other pump options. Then

(5.3‑106)

\[\Delta a_{2} = 0\]

and

(5.3‑107)

\[\Delta a_{3} = \Delta t \frac{\text{dH}}{\text{dW}}\]

with \(\text{dH}/\text{dw}\) being evaluated numerically from the table of \(\overline{H}\) vs. \(\overline{w}\):

(5.3‑108)

\[\frac{\text{dH}}{\text{dw}} = \frac{H\left( w + .01 w_{0} \right) - H\left( w \right)}{.01 w_{0}}\]

where \(w_0\) is the initial steady state flow rate, \(w\) is the current flow rate, and \(H\) is the pump head.

5.3.4.3. Electromagnetic Pumps

The electromagnetic pump is modeled as a pipe element. The expression for the pump head for the electromagnetic pump is

(5.3‑109)

\[\Delta p_{\text{p}} = H_{\text{s}}\left( t \right) \left( 1 - \frac{v_{\text{Na}}}{v_{\text{sy}}} \right)\]

with

(5.3‑110)

\[v_{\text{Na}} = \frac{w}{\rho A}\]

where

\(\Delta p_{\text{p}}\) = the pump head

\(H_{\text{s}} \left( t \right)\) = the pump stall head

\(v_{\text{Na}}\) = the sodium velocity at the beginning of the time interval

\(w\) = the pipe flow rate

\(A\) = the pipe area

\(\rho\) = the sodium density

\(v_{\text{sy}}\) = user-supplied synchronous magnetic field velocity

The quantity

(5.3‑111)

\[\frac{H_{\text{s}} \left( t \right)}{H_{\text{s}} \left( o \right)}\]

is a user-supplied table of normalized stall head as a function of time.

The contributions to the \(a\)’s in Eqs. 5.2-10 through 5.2-16 for the electromagnetic pump are

(5.3‑112)

\[\Delta a_{\text{o}} = \frac{L_{\text{p}}}{A_{\text{p}}}\]

(5.3‑113)

\[\Delta a_{1} = \Delta t \Delta p_{\text{p}} \left( t_{3} \right)\]

(5.3‑114)

\[\Delta a_{2} = \Delta t \left\lbrack H_{\text{s}}\left( t_{4} \right) - H_{\text{s}}\left( t_{3} \right) \right\rbrack \left( 1 - \frac{v_{\text{Na}}}{v_{\text{sy}}} \right)\]

(5.3‑115)

\[\Delta a_{3} = - \Delta t H_{\text{s}} \left( t_{3} \right) v_{\text{Na}}\]

where

\(L_{\text{p}}\) = the length of the pump element

\(A_{\text{p}}\) = the flow area of the pump element

\(\Delta p_{\text{p}} \left( t_3 \right)\) = the pump head evaluated at the beginning of the time interval

\(\Delta t\) = the time interval

\(H_{\text{s}} \left( t_3 \right)\) = the stall head at the beginning of the time interval

\(H_{\text{s}} \left( t_4 \right)\) = the stall head at the end of the time interval

5.3.4.4. ALMR EM Pumps

In the ALMR design, the primary pumps contain motor-generators that extend the coastdown times of these EM pumps. Since this combination of EM pumps and motor-generators cannot be modeled well with previous SAS4A/SASSYS‑1 pump options, the ALMR program developed a new pump model to handle this configuration. The new model uses a model similar to that used by General Electric in their ARIES-P code. It is based on head and efficiency data obtained by GE and transmitted to ANL (5-29).

In the ALMR design, a synchronous motor is running all of the time during normal operation, but the power to the EM pump does not go through the motor as long as the normal pump power is available. If normal pump power is lost, then the motor becomes a generator, and a switch is thrown automatically to supply voltage from the motor-generator to the pump. The pump coastdown rate is then determined by the inertia of the motor. The motor is designed such that it will initially supply 60% of nominal voltage to the pump. Thus, when normal power is lost and the motor-generator power is switched on there is a sudden drop in pump head and flow followed by a gradual coastdown.

Controlling the Trip Time

There are two options for controlling the time at which the ALMR EM Pump cuts over to the motor-generator. The first method is to set the trip time in input variable APMPHD(7,IPMP) in block PMR4IN. The second method is to set a dynamic trip time using a function. In this case, the Function Block ID is set in input variable ILRPMP. A single argument is passed to the function containing the value of the time at the end of the current PRIMAR-4 time step. If the time exceeds the value returned by the function, then pump cuts-over to the motor generators, and remains in a tripped state for the remainder of the simulation.

Pump Head

The pump head is correlated with an expression of the form

(5.3‑116)

\[\overline{H} = \left( \frac{\overline{V}}{\overline{f}} \right)^{3.5}h_{\text{n}}\left( \frac{\overline{w}}{\overline{f}} \right) - L_{\text{f}}{\overline{w}}^{2}\]

where the normalized terms are defined as

(5.3‑117)

\[\overline{H} = \frac{H}{H_{\text{r}}}\]

(5.3‑118)

\[\overline{V} = \frac{V}{V_{\text{r}}}\]

(5.3‑119)

\[\overline{f} = \frac{f}{f_{\text{r}}}\]

(5.3‑120)

\[\overline{w} = \frac{w}{w_{\text{r}}}\]

where

\(H\) = pump head

\(H_{\text{r}}\) = rated head

\(V\) = pump voltage

\(V_{\text{r}}\) = rated voltage

\(f\) = frequency

\(f_{\text{r}}\) = rated frequency

\(w\) = mass flow rate

\(w_{\text{r}}\) = rated mass flow rate

\(L_{\text{f}}\) = friction loss coefficient

and \(h_{\text{n}}\) is a head curve correlated as

(5.3‑121)

\[h_{\text{n}}\left( \frac{\overline{w}}{\overline{f}} \right) = \sum_{\text{j} = 1}^{5}{a_{\text{j}}\left( \frac{\overline{w}}{\overline{f}} \right)^{j - 1}}\]

with the coefficients \(a_{\text{j}}\) determined by a least-squares fit to the data.

Pump Efficiency

The pump efficiency, \(\varepsilon_{\text{f}}\), is correlated as

(5.3‑122)

\[\varepsilon_{\text{f}} = F \left( \overline{V} \right) G \left( \frac{\overline{w}}{\overline{f}} \right) \varepsilon_{\text{fr}}\]

with

(5.3‑123)

\[F \left( \overline{V} \right) = \sum_{\text{j} = 1}^{7}{b_{\text{j}}{\overline{V}}^{j - 1}}\]

(5.3‑124)

\[\begin{split} G \left( \frac{\overline{w}}{\overline{f}} \right) = \begin{cases} 0.01 & \text{if }\frac{\overline{w}}{\overline{f}} \geq 5 \\ \sum_{\text{j} = 1}^{9}{c_{\text{j}} \left( \frac{\overline{w}}{\overline{f}} \right)^{j - 1}} & \text{if }\frac{\overline{w}}{\overline{f}} \leq 5 \\ \end{cases}\end{split}\]

and \(\varepsilon_{\text{fr}}\) is the rated efficiency

Pump Voltage

Before the cut-over to the motor-generator, the pump voltage is assumed to be constant at its rated value. Also, the frequency is constant at its rated value. Immediately after cut-over, the voltage drops to a fraction, \(V_{\text{fr}}\), of its initial value. Then the voltage is proportional to the square of the frequency, so after cut-over the voltage is

(5.3‑125)

\[\overline{V} = V_{\text{fr}}{\overline{f}}^{2}\]

Motor Speed

The equation for the motor speed, \(s\), is

(5.3‑127)

\[\frac{\text{ds}}{\text{dt}} = - \frac{\tau_{\text{p}} + \tau_{\text{l}}}{I}\]

where

\(\tau_{\text{p}}\) = pump torque

\(\tau_{\text{l}}\) = friction loss

\(I\) = moment of inertia

Note that the motor speed and the pump frequency are the same:

(5.3‑128)

\[f = s\]

The pump torque is given by

(5.3‑129)

\[\tau_{\text{p}} = \frac{Hw}{\varepsilon_{\text{f}} \rho s}\]

where

\(\rho\) = liquid density

The friction loss in the motor is assumed to have the form

(5.3‑130)

\[\tau_{\text{l}} = \tau_{\text{r}} L_{\text{m}} s\]

where \(L_{\text{m}}\) is a loss coefficient and \(\tau_{\text{r}}\), the rated torque, is given by equation 5.3-129 with rated values used for all terms.

Correlations to Pump Data

Reference 5-29 transmitted the data taken for the pump. This data has been fit by a least-squares fitting program to give the parameters listed in Table 5.3.1 for use in equations 5.3-121, 5.3-123, and 5.3-124. Also a value of .07592 is used for \(L_{\text{f}}\) in equation 5.3-116. Table 5.3.2 lists the data from Ref. 5-29, as well as the head and efficiency values calculated using the correlations of equations 5.3-116, 5.3-121, 5.3-122, and 5.3-124 with the coefficients in Table 5.3.1. Also, some of this data is plotted in Figure 5.3.1 and Figure 5.3.2. It can be seen that the correlations match the data well except for a couple of points.

Table 5.3.1 Correlation Coefficients for Use with the ALMR EM Pump Model

\(j\)	\(a_{\text{j}}\)	\(b_{\text{j}}\)	\(c_{\text{j}}\)
1	1.133	-.148
2	.996	7.110	-51.235
3	-2.498	-15.972	684.934
4	6.056	9.942	-3483.628
5	-4.611	12.024	9119.690
6		-18.536	-13449.761
7		6.577	11279.948
8			-5014.503
9			915.555

Table 5.3.2 Pump Head and Efficiency for the ALMR EM Pump Model

Normalized Voltage	Normalized Frequency	Normalized Flow	Normalized Head - Measured	Normalized Head - Fit	Efficiency - Measured	Efficiency - Fit
1.000	1.000	1.148	0.042	0.041	0.115	0.133
1.000	1.000	1.124	0.250	0.242	0.505	0.469
1.000	1.000	1.086	0.500	0.524	0.781	0.807
1.000	1.000	1.000	1.000	1.000	1.000	0.997
1.000	1.000	0.800	1.483	1.494	0.928	0.915
1.000	1.000	0.600	1.508	1.514	0.710	0.709
1.000	1.000	0.400	1.399	1.389	0.469	0.468
1.000	1.000	0.200	1.265	1.270	0.229	0.229
1.000	1.000	0.0	1.134	1.133	0.0	0.0
0.627	0.778	0.886	0.042	0.042	0.183	0.256
0.627	0.778	0.862	0.167	0.158	0.551	0.600
0.627	0.778	0.824	0.333	0.314	0.817	0.879
0.627	0.778	0.762	0.581	0.500	0.970	0.932
0.628	0.778	0.762	0.581	0.505	0.970	0.932
0.312	0.472	0.532	0.042	0.052	0.318	0.381
0.312	0.472	0.520	0.083	0.097	0.529	0.608
0.312	0.472	0.495	0.167	0.178	0.773	0.848
0.312	0.472	0.476	0.227	0.226	0.863	0.884
1.202	1.111	1.143	1.306	1.144	1.008	1.009
0.929	0.944	0.952	0.905	0.912	0.998	1.003
0.820	0.833	0.857	0.734	0.835	0.986	0.981
0.519	0.667	0.667	0.444	0.415	0.954	0.932
0.437	0.556	0.571	0.327	0.383	0.917	0.920
0.251	0.500	0.476	0.227	0.096	0.855	0.789
0.219	0.389	0.381	0.145	0.143	0.757	0.757
0.153	0.278	0.286	0.082	0.111	0.567	0.602
0.071	0.222	0.190	0.037	0.025	0.268	0.255
0.027	0.111	0.095	0.009	0.010	0.026	0.031

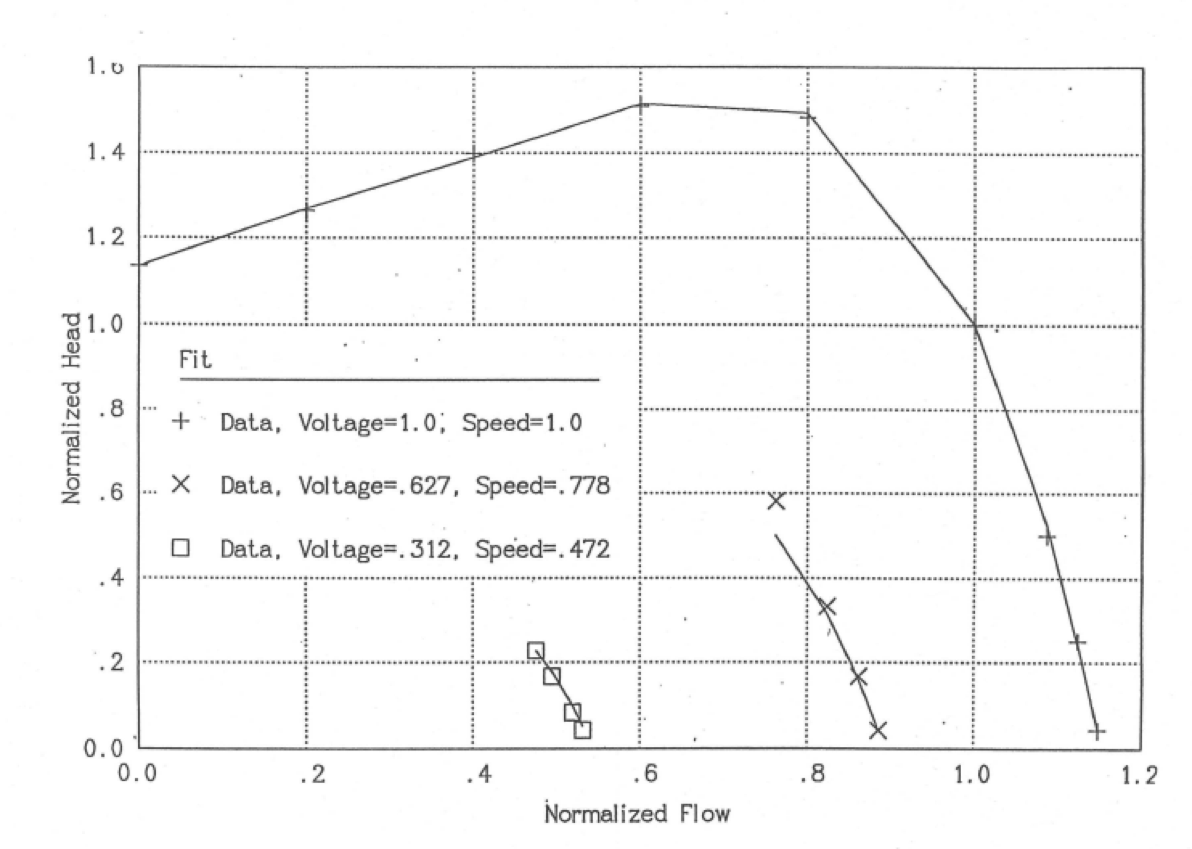
Figure 5.3.1 Pump Head, Data and Fits for the ALMR EM Pump Model.

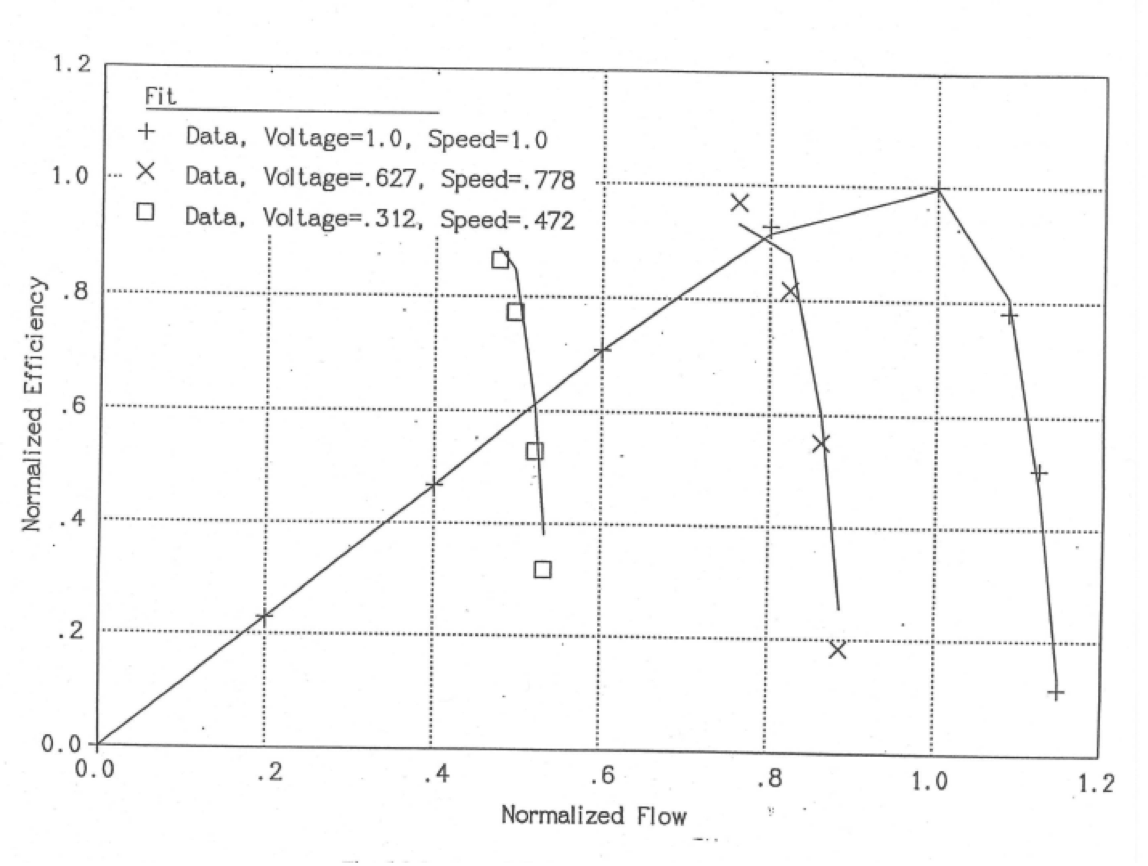
Figure 5.3.2 Pump Efficiency, Data and Fits for the ALMR EM Pump Model.

5.3.5. Valves

SAS4A/SASSYS‑1 contains a simple valve treatment in which the user can specify the valve pressure loss coefficient as a function of time. The pressure drop, \(\Delta p_{\text{v}}\), through a valve is calculated as

(5.3‑131)

\[\Delta p_{\text{r}}\left( t \right) = G_{2}\left( t \right) \frac{w \left| w \right|}{2\rho A^{2}}\]

where

\(w\) = coolant flow rate through the valve

\(\rho\) = coolant density

\(A\) = nominal valve flow area

\(G_2\) = valve coefficient

The user supplies a table of \(G_2\) as a function of time. The table is used to obtain an average value of \(G_2\) for each step of the transient. With this treatment, a valve is never entirely shut; although \(G_2\) can be made very large so that the flow through the valve becomes very small.

Some care must be taken in setting the input for a valve. The table of \(G_2\) vs. \(t\) goes in the DTMPTB and TMPMTB input arrays, but in addition \(G_2 \left( t=0 \right)\) goes in the input variable G2PRDR (ELL) for the element IELL corresponding to the valve. During the steady-state initialization, G2PRDR may be adjusted by the code if necessary to achieve a steady-state pressure balance. At the end of the steady-state initialization, if G2PRDR does not match the table entry for \(t=0\), then a constant value is added to all of the entries in the DTMPTB table for the valve so that the table does match G2PRDR at \(t=0\). Up to eight valves can be used. Each valve can use its own separate valve coefficient table. It is also possible to use the same table for two or more valves but this option must be used with care. All valves using the same table should have the same steady-state valve coefficients and the same time dependence. Also, if a valve table is adjusted to achieve a steady-state pressure balance for one valve, the adjustment may not be appropriate for other valves using the same table.

5.3.6. Check Valves

SAS4A/SASSYS‑1 contains a simple check valve treatment in which the user can specify the valve orifice coefficient as a function of coolant flow rate. Every time step an orifice coefficient (\(G_2\) in Eq. 5.3-35) is re-set using a user-supplied table of orifice coefficient vs. normalized flow rate, with a flow rate normalized to its steady-state value. Other than the variable orifice coefficient, a check valve is treated the same as a pipe, as described in Section 5.3.3.