9.2. Model Formulation¶
9.2.1. Fission Gas¶
Reference 9‑2 reviews the current understanding of fission gas generation, release, and transport in metallic fuel. DEFORM‑5 does not currently model steady-state fission gas generation and migration, but assumes that an independent assessment has been made to determine the fission gas content in the fuel element at the initial steady-state. The fission gas inventory is specified as input in the form of a axially uniform fuel element pressure at the SAS4A/SASSYS‑1 initial reference temperature. The steady-state fission gas mass is then calculated from plenum and available pore volumes using the ideal gas law. Transient fuel element and internal fuel pressures are calculated using the calculated fission gas mass and the transient temperatures in the ideal gas formulation.
9.2.2. Fuel/Cladding Eutectic Alloy Formation¶
Uranium‑ and uranium/plutonium‑based metallic fuels interact chemically with iron-based cladding to form low-melting-point eutectic alloys. For typical metallic fuel element geometry and for the transient sequences analyzed with SAS4A/SASSYS‑1, the impact of this phenomena is to form a molten region at the fuel/cladding interface if the fuel is contacting the cladding, if the contact temperature has been raised to a sufficient level to cause eutectic alloy formation, and if the contact temperature has been held at the elevated level long enough to form the eutectic alloy, given the formation rate at that temperature. Figure 9.2.1 shows a binary phase diagram for uranium and iron [9‑3]. This diagram shows that in equilibrium, liquid material may be formed at a temperature as low as 725°C for an alloy that is 89 wt. % uranium.
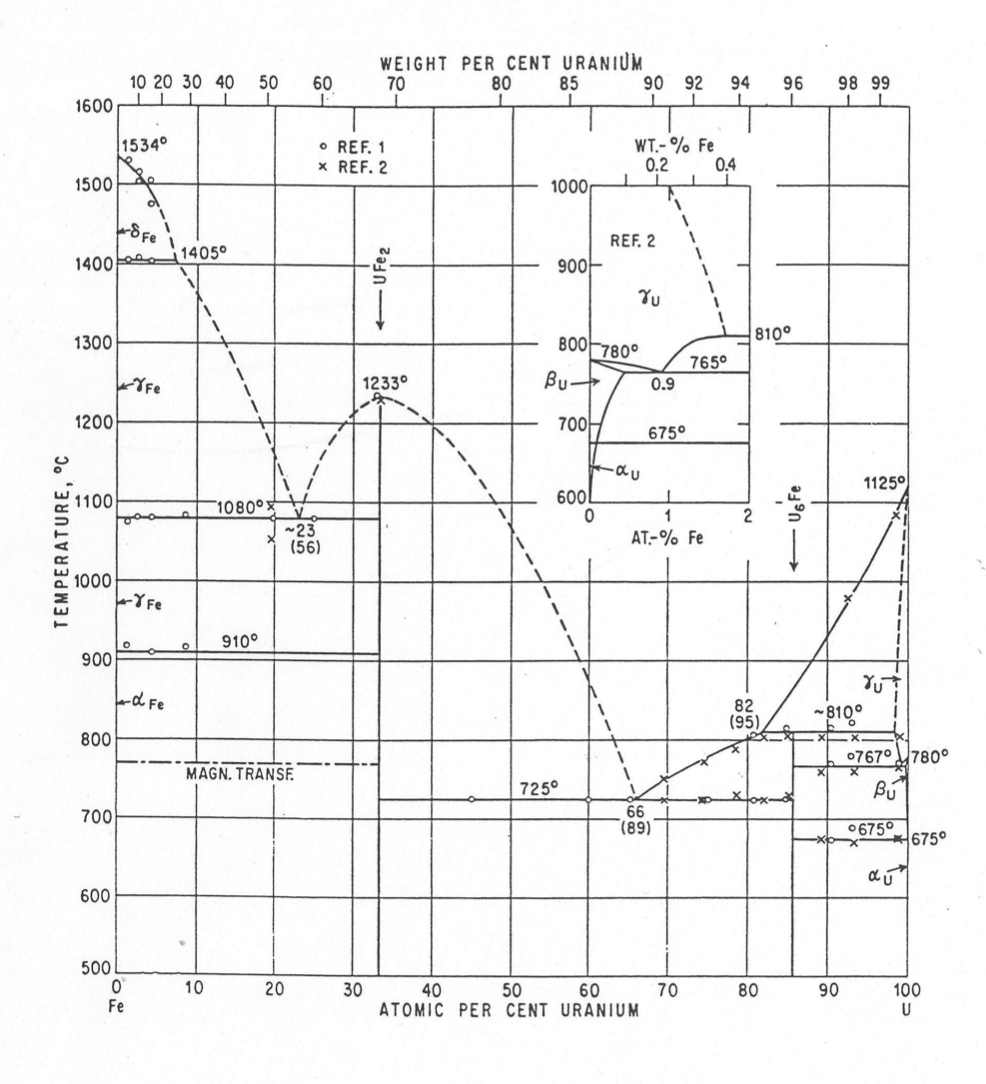
Figure 9.2.1 Uranium-Iron Phase Diagram [9‑3].¶
In SAS4A/SASSYS‑1 analyses, where the fuel/cladding behavior model is concerned mainly with predicting margin to cladding failure, cladding failure time, and cladding failure location, the primary importance of eutectic alloy formation at the fuel cladding interface is an effective thinning of the cladding, and a lessening of its ability to contain the internal, hydrostatic pressure due to released fission gas. To quantify the cladding thinning in DEFORM‑5, the correlation developed by Bauer [9‑4] for the eutectic penetration rate as a function of absolute temperature is used. This correlation is
(9.2‑1)
except in the range 1353 K (1080°C) to 1506 K (1233°C) where
(9.2‑2)
Where \(\dot{r}\) is the eutectic penetration rate in m/s, and \(T\) is the absolute temperature in Kelvins. This correlation is based on 1) tests in which iron capsules were dipped into molten uranium and uranium/iron alloy baths [9‑5], 2) tests of EBR-II Mark-II driver fuel [9‑6, 9‑7, 9‑8], and 3) tests of ternary alloy fuel (U‑19Pu‑10Zr) clad with stainless steel (D9) [9‑4]. Waltar and Kelman [9‑5] associated the rate increase in the range from 1353 K to 1506 K with the formation characteristics of the compound UFe2. Equation (9.2-1) and Equation (9.2-2) are used in DEFORM‑5 to calculate the cladding penetration as a function of time and the effective cladding thickness at each axial location and in each SAS4A/SASSYS‑1 channel.
9.2.3. Clad Strain¶
In DEFORM‑5, a calculation of the cladding strain is performed to provide input to the cladding failure assessment. The basic approach adopted for calculating cladding strain is that developed by DiMelfi and Kramer [9‑9, 9‑10] in their studies on plastic flow in steel cladding, and implemented in the FPIN2 computer code (see Section 11.3.6). The hoop stress in the cladding, \(\sigma_{\theta}\), is determined for a thin shell under internal pressure loading:
(9.2‑3)
where \(P\) is the internal pressure, \(P_{\text{ch}}\) is the coolant channel pressure, \(a\) is the inner cladding radius, and \(h\) is the cladding thickness. Assuming the hydrostatic loading of a thin, cylindrical shell, the hoop stress is converted to an equivalent stress:
(9.2‑4)
and this stress is then used in the flow equation developed by DiMelfi and Kramer:
(9.2‑5)
where \(\dot{\epsilon}\) is the equivalent strain rate, \({\dot{\epsilon}}_{\text{oos}}\) is a material constant, \(\sigma\) is the equivalent stress, \(\sigma_{\text{so}}\) is the saturation stress, \(m\) is the stress exponent, \(\frac{Q}{R}\) is the creep activation temperature, and \(T\) is the absolute steel temperature.
This formulation was chosen because it allows the use of the same model for all cladding types of interest. Through the use of appropriate cladding parameters, SS316, D9, and HT‑9 can all be modeled within the DEFORM‑5 context. (In the absence of data, the following parameters for SS 316 are used for D9).
For type 316 stainless steel, Kramer and coworkers [9‑11] derived the following parameters:
\(m\) = 5.35
\(\frac{Q}{R} = 38,533\) K
\({\dot{\epsilon}}_{\text{oos}} = 1.062 \times 10^{14}\) s-1
\(\sigma_{\text{so}} = \left( 2000 - 9.12 T \right) \left( 92,000 - 40.2 T \right)\) Pa
For type HT‑9 stainless steel, Kramer and coworkers [9‑12] derived the following parameters:
\(m = 2.263\)
\(\frac{Q}{R} = 36,739\) K
\({\dot{\epsilon}}_{\text{oos}} = 5.1966 \times 10^{10}\) s-1
\(\sigma_{\text{so}} = 3.956 \times 10^{-3} \times 2.12 \times 10^{11} \left( 1.144 - 4.856 \times 10^{-4} T \right)\) Pa
9.2.4. Cladding Failure¶
The determination of cladding breach, or margin to cladding breach, is based on the eutectic thinning of the cladding and the reduced ability to contain the internal pressure. Besides the eutectic thinning, the cladding wall thickness is reduced as plastic flow takes place. Different accident scenarios and pin conditions lead to different modes of breach, whether through cladding penetration or plastic strain or a combination.
In the DEFORM‑5 calculation, the time‑dependent cladding damage fraction is calculated based on the time remaining to breach, following Kramer and DiMelfi’s assessment [9‑13] of the TDC‑2 transient damage correlation for cold‑worked 316 (and also for D9) stainless steel fuel pin cladding [9‑14]:
(9.2‑6)
where
\(t_{\text{r}}\) = time to rupture, hours
\(A\) = -43.06
\(B\) = 7.312
\(C\) = -1.73
\(Q_{1}\) = 41339
\(D\) = 1000
\(E\) = 200
\(F\) = 0.438
\(\begin{eqnarray} \sigma^{*} & = & 775 - \left\lbrack 387.5 - 387.5\tanh\left( \frac{D - TI}{E} \right)\right\rbrack\tanh\left( \frac{\phi t}{2.0} \right) \\& + & 125\left\lbrack \tanh\left( \frac{\sigma}{550} \right)^{10} \right\rbrack\left\lbrack 1 - \tanh\left( \frac{\text{TI}}{583} - F \right)^{25} \right\rbrack\tanh\left( \frac{\phi t}{2.5} \right)\end{eqnarray}\)
\(\text{TRAMP} = -0.28 + 1.18 \tanh{\left(-0.5 \lbrack \ln{\dot{T}} - 1 \rbrack \right)}\)
\(\sigma\) = hoop stress, MPa (use thin wall formula with midwall tube diameter)
\(\phi t\) = fluence n/cm2, E > 0.1 MeV, x1022
\(T\) = transient temperature, K
\(\text{TI}\) = steady-state irradiation temperature, K
\(\dot{T}\) = transient temperature ramp rate, K/sec
In DEFORM‑5, the fast fluence is calculated from the input local linear power, the channel flux-to-power ratio, and number of full-power days of steady-state irradiation.
For HT‑9, the time remaining to breach is assumed to be given by [9‑15]:
(9.2‑7)
where
\(t_{\text{r}}\) = time to rupture, seconds
\(\ln\theta = A + B\ln{\ln\left( \frac{\sigma^{*}}{\sigma} \right)}\)
\(A = - 34.8 + \tanh{\left( \frac{\sigma - 200}{50} \right) + C}\)
\(B = \frac{12}{1.5 + 0.5\tanh\left( \frac{\sigma - 200}{50} \right)}\)
\(C = - 0.5\left\lbrack 1 + \tanh\left( \frac{\sigma - 200}{50} \right) \right\rbrack 0.75\left\lbrack 1 + \tanh\left( \frac{\dot{T} - 58}{17} \right) \right\rbrack\)
\(\sigma^{*}\) = 730 MPa
\(\sigma\) = hoop stress, MPa
\(T\) = transient temperature, K
\(\dot{T}\) = heating rate, K/s
\(Q\) = 70170 cal/mole
\(R\) = 1.986 cal/mole-K