4.5. Net Reactivity¶
For applications other than EBR-II, the net reactivity in Eq. 4.2-4 is the sum of nine reactivity components:
(4.5‑1)
where
\(\delta k_{\text{p}}\) = User-programmed reactivity,
\(\delta k_{\text{cs}}\) = Control system reactivity,
\(\delta k_{\text{D}}\) = Fuel Doppler feedback reactivity,
\(\delta k_{\text{d}}\) = Fuel, cladding, and structure axial expansion feedback reactivity,
\(\delta k_{\text{Na}}\) = Coolant density or voiding feedback reactivity,
\(\delta k_{\text{re}}\) = Core radial expansion feedback reactivity,
\(\delta k_{\text{cr}}\) = Control rod drive expansion feedback reactivity,
\(\delta k_{\text{fu}}\) = Fuel relocation reactivity feedback,
\(\delta k_{\text{cl}}\) = Cladding relocation reactivity feedback.
The reactivity feedback models available for these components are covered in the sections that follow. For EBR-II applications, the net reactivity is calculated as formulated in Section 4.5.9.
4.5.1. User-Programmed Reactivity¶
The user-programmed reactivity is specified by the user at execution time as either an input table or as subprogram FUNCTION PREA. It is intended to be used as a means of specifying any reactivity effect not explicitly modeled as a feedback. An example might be the simulation of a control rod withdrawal or insertion, or the dropping of a fuel subassembly during reloading.
The user-programmed reactivity option is triggered by setting IPOWER to 0. For NPREAT equal to
0, the value returned by the user-supplied subroutine function PREA is
used as the programmed reactivity. For NPREAT > 0, NPREAT gives the
number of pairs of values of programmed reactivity and time input on the
standard input file in PREATB and PREATM. A maximum of twenty pairs of programmed reactivity and
time may be entered in PREATB and PREATM. These data are then either
used directly or fit to curves according to the user’s specification of
input data IFIT.
4.5.2. Control System Reactivity¶
The control system reactivity is the value supplied by the reactivity control signal (JTYPE = -1) generated by the control system model (see Chapter 6 and Input Block 5-INCONT).
4.5.3. Fuel Doppler Feedback Reactivity¶
The fuel Doppler reactivity effect at any axial location in a subassembly is estimated from
(4.5‑2)
where \(T_{\text{f}}\) is the radial mass-averaged fuel temperature for that axial location, and \(\alpha_{\text{D}}\) is the local fuel Doppler coefficient, an input quantity. To obtain the Doppler reactivity feedback at time \(t\), Eq. 4.5-2 is integrated from steady-state conditions to conditions at time \(t\) to obtain
(4.5‑3)
Eq. 4.5-3 is used at each axial location where a fuel temperature is calculated. The local fuel Doppler coefficient, \(\alpha_{\text{D}}\), is adjusted linearly between the input coolant-in (flooded) and coolant-out (voided) values to correct for the effect of coolant voiding on neutron leakage.
The coolant-in and coolant-out Doppler coefficients are entered as ADOP
and BDOP, and the axial weighting
of the Doppler coefficients is input as WDOPA.
4.5.4. Fuel, Cladding, and Structure Axial Expansion Feedback Reactivity¶
4.5.4.1. Simple Axial Expansion Reactivity Model¶
A simple model for the reactivity effects of thermal expansion of fuel and cladding is included in SAS4A/SASSYS‑1. The simple thermal expansion feedback model is based on a few assumptions. It is assumed that before the start of the transient, a combination of fuel cracking, fuel re-structuring, and stress relaxation cause the gap between the fuel and the cladding to close, but there is little contact force between the fuel and the cladding. During the transient, if the cladding expands faster than the fuel, then the fuel-cladding gap opens, and the fuel can expand freely in the axial direction. If the fuel expands faster than the cladding, then the fuel binds with the cladding, and the axial expansion is determined by balancing the axial forces between the fuel and the cladding. Slip between fuel and cladding is ignored in this case. The axial expansion feedback is calculated separately for each channel. The formulation for each channel follows.
For each axial node, \(j\), in the core, the fuel and cladding expansion fractions are calculated as
(4.5‑4)
and
(4.5‑5)
where
\(\alpha_{\text{f}}\) = fuel thermal expansion coefficient
\(\alpha_{\text{e}}\) = cladding thermal expansion coefficient
\(T_{\text{f}}\) = mass-averaged fuel temperature for axial node j
and
\(T_{\text{e}}\) = cladding mid-point temperature
If \(\epsilon_{\text{e}}\left( j \right)\) is greater than \(\epsilon_{\text{f}}\left( j \right)\), then the fuel axial expansion for node \(j\) is
(4.5‑6)
and the cladding expansion is
(4.5‑7)
where \(D_{\text{z}}\) is the nominal axial height of the node. If \(\epsilon_{\text{f}}\left( j \right)\) is greater than or equal to \(\epsilon_{\text{e}}\left( j \right)\), then a simple balance between the axial forces of the fuel and cladding gives
(4.5‑8)
and
(4.5‑9)
where
\(Y_{\text{f}}\) = fuel Young’s modulus
\(Y_{\text{e}}\) = cladding Young’s modulus
\(A_{\text{f}}\) = nominal cross-sectional area of the fuel
and
\(A_{\text{e}}\) = nominal cross-sectional area of the cladding
The reactivity calculation is based on the fuel and cladding worth tables used by the code. First an unexpanded axial mesh, \(z_{0}\left( j \right)\), is calculated using
(4.5‑10)
and
(4.5‑11)
Note that \(z_{0}\) is zero at the bottom of the lower axial blanket.
New, expanded axial meshes for the fuel and cladding, \(z_{\text{nf}}\left( j \right)\) and \(z_{\text{ne}}\left( j \right)\), are calculated using
(4.5‑12)
(4.5‑13)
(4.5‑14)
and
(4.5‑15)
where
(4.5‑16)
and
(4.5‑17)
SAS4A/SASSYS‑1 uses a fuel worth per unit mass, \(R_{\text{f}}\left( j \right)\), and a cladding worth per unit mass, \(R_{\text{e}}\left( j \right)\), defined on the original mesh, \(z_{0}\left( j \right)\). If node \(j\) has been shifted and expanded so that
(4.5‑18)
and
(4.5‑19)
as in Figure 4.5.1, then \(\Delta\rho_{\text{f}}\left( j \right)\), the fuel contribution to axial expansion feedback from node \(j\) is calculated as
(4.5‑20)
A similar expression is used to calculate \(\Delta\rho_{\text{e}}\left( j \right)\), the cladding contribution to axial expansion feedback. If \(z_{\text{nf}}\left( j + 1 \right)\) has expanded past \(z_{0}\left( j + 2 \right)\), then a summation over the appropriate nodes is used instead of Eq. 4.5-20.
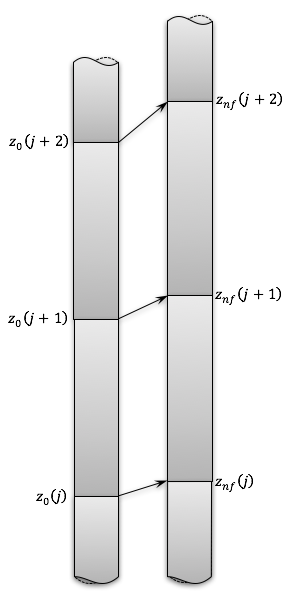
Figure 4.5.1 Original and Expanded Fuel Axial Meshes¶
By default, SAS4A/SASSYS‑1 calculates the axial expansion of fuel and cladding as described above. In addition to the gap-dependent model described above, the user can choose cladding-controlled expansion, independent free expansion, or force balance controlled expansion at all times. Cladding-controlled expansion may be appropriate for cases where there is no gap between fuel and cladding and the fuel Young’s modulus is much less than the cladding Young’s modulus. In this case, the cladding expansion is calculated by Eq. 4.5-7, and the fuel expansion is set equal to the cladding expansion. Independent free expansion may be appropriate for cases where the gap is expected to be maintained throughout the transient; the expansion is then determined by Eqs. 4.5-6 and 4.5-7, without the need for force balance. The continual force balance option may be appropriate for cases where the fuel and cladding are expected to be in contact at the initial condition, and remain in contact throughout the transient. In which case, expansion is determined by Eqs. 4.5-8 and 4.5-9, regardless of the relative expansion rates of fuel and cladding.
A feature has been added to include the reactivity effect associated with the axial thermal expansion of structure during the transient. This feature may be used, for instance, to treat the thermal expansion of the subassembly duct walls. Structure is considered to be free, and expansion is calculated in an analogous way as the independent free expansion model for fuel and cladding. That is, equations for the structure expansion are written similar to Eqs. 4.5-5 and 4.5-7, with no need for force balance. An expression for the reactivity change in node \(j\), \(\Delta \rho_{\text{s}} \left( j \right)\), is written similar to Eq. 4.5-20, based on changes in the grid calculated in an analogous fashion as Eq. 4.5-15.
The total reactivity change, \(\delta k_{\text{d}}\), is
(4.5‑21)
where \(\epsilon_{\text{ex}}\) is an effective axial expansion multiplier.
The summation in Eq. 4.5-21 is only over the core nodes. The axial blankets are ignored in the fuel expansion feedback calculations. In order to obtain an accurate value for the axial expansion reactivity feedback, the fuel worth input for the upper axial blanket nodes must be the worth of core fuel in the blanket region.
The cladding, fuel, and structure worth used in Eq. 4.5-20 are input in
arrays CLADRA, FUELRA, and STRCRA. The effective axial expansion multiplier in Eq. 4.5-21 is
input as EXPCFF. Thermal expansion
coefficients for fuel, cladding, and structure are input in FUELEX,
CLADEX, and StructEX. The
initial mass of cladding and structure in each channel is computed using
the density DENSS. The simple axial
expansion reactivity model is invoked by IAXEXP with the axial expansion mode option selection in MODEEX.
4.5.4.2. DEFORM-4 Axial Expansion Reactivity Model¶
For any channel in which the DEFORM-4 module (see Chapter 8) has been
specified, the axial expansion reactivity feedback will be calculated as
described in Eqs. 4.5-10 through 4.5-21 but using fuel and cladding
expanded axial mesh heights as calculated by DEFORM-4. The DEFORM-4
effective axial expansion multiplier is entered as EXPCOF.
4.5.5. Coolant Density Feedback Reactivity¶
Reactivity feedback effects from either single-phase coolant density
changes or two-phase coolant boiling are calculated using the input
coolant void reactivity worth table VOIDRA. The reactivity feedback from coolant density and voiding changes
is calculated from
(4.5‑22)
where
\(\epsilon_{\text{d}}\) = sodium density multiplier
\(\left( \rho_{c} \right)_{ij}\) = coolant void worth in axial segment \(j\) of channel \(i\)
and
\(\alpha_{ij}\) = average coolant void fraction in segment \(j\) of channel \(i\).
The local coolant void fraction is calculated based on either a) liquid
coolant density changes from the initial steady-state condition, or b)
combined liquid density and boiling-induced voiding density changes from
the steady-state condition. The sodium density multiplier is entered as COLFAC.
4.5.6. Radial Expansion Feedback Reactivity¶
4.5.6.1. Simple Radial Expansion Reactivity Model¶
Two radial expansion feedback models are available in SAS4A/SASSYS‑1: a simple model described here and a more detailed model described in Section 4.5.6.2.
The simple radial expansion feedback model in SAS4A/SASSYS‑1 is based on a model by Huebotter [4-4]. The radial growth of the core is determined by the expansion of the lower grid support structure and by the expansion of the duct walls at the above core load pads. The expansion of the lower grid support structure is assumed to be proportional to the rise in the subassembly inlet temperature above its initial steady-state value. The expansion at the location of the above core load pads is assumed to be proportional to the change in the average structure temperature at this location.
The equations actually used in SAS4A/SASSYS‑1 are
(4.5‑23)
where
\(t\) = time, s
\(\delta k_{\text{re}}\) = reactivity change due to radial expansion, $
\(C_{\text{re}}\) = radial expansion coefficient, $/K
\(\Delta T_{{\text{in}}}\) = \(T_{{\text{in}}}\left( t \right) - T_{{\text{in}}}\left( t_{1} \right)\), K
\(T_{{\text{in}}}\) = coolant inlet temperature, K
\(t_{1}\) = time at the end of the first main time step, s
\(\text{XMC}\) = distance from nozzle support point to core midplane, m
\(\text{XAC}\) = distance from nozzle support point to above core load pad, m
(4.5‑24)
(4.5‑25)
\({\overline{T}}_{\text{SLP}}\) = average structure temperature at the above core load pads
\(T_{\text{SLP}}\left( i,t \right)\) = structure temperature (outer structural radial node) in channel i at the axial node corresponding to the above core load pad
\(i\) = channel number
\(N_{\text{s}}\left( i \right)\) = number of subassemblies represented by channel \(i\)
\(f_{\text{i}} = \begin{cases} 1 & \text{if channel is to be included in the average} \\ 0 & \text{if channel is not to be included} \\ \end{cases}\)
An option has been included in the code to use the inlet plenum wall
temperature instead of the coolant inlet temperature for
\(T_{{\text{in}}}\). This option can be used to account for
time delays in the heating of the lower grid support structure. Note
that for coding simplicity the temperatures at the end of the first main
time step are used as the reference values, rather than using
steady-state temperatures for the reference. This makes very little
difference in the results, since the changes in the inlet temperature
and the outer structure node temperature above the core are normally
extremely small during the first time step. Also, the user can choose
which channels will be included in the averaging of Eq. 4.5-25 by
specifying \(f_{\text{i}}\) for each channel using IRDEXP.
This model was not explicitly set up to account for subassembly bowing
or flowering of the core, but the user can set arbitrary values for
\(C_{\text{re}}\) and
\(\left\lbrack \frac{{\text{XMC}}}{{\text{XAC}}} \right\rbrack\)
in Eq. 4.5-23. Therefore, if the bowing reactivity effect is
proportional to \(\Delta{\overline{T}}_{{\text{SLP}}}\) or to
\(\Delta{\overline{T}}_{{\text{SLP}}} - \Delta{\overline{T}}_{{\text{in}}}\),
then bowing reactivity can be accounted for by adjusting
\(C_{\text{re}}\) and
\(\frac{{\text{XMC}}}{{\text{XAC}}}\), which are
entered as input variables RDEXPC and XMCXAC. The simple radial expansion model is invoked by specifying
IRADEX.
4.5.6.2. Detailed Radial Expansion Reactivity Model¶
The basic radial core expansion reactivity feedback model described in Section 4.5.6.1 incorporated several major assumptions that restricted the ability of the model to calculate the reactivity feedback accurately, particularly in extended transients. These assumptions include the following:
The reactivity feedback is determined solely by thermal expansions of the grid support plate and load pad region, with all regions having the same thermal expansion coefficient.
The displacement of the core midplane is sufficient to estimate the reactivity feedback from radial core expansion.
All of the subassembly load pads are in contact throughout the transients.
With these assumptions, the model does not explicitly account for subassembly bowing, and is not capable of calculating changes in core loading conditions during the course of a transient. This deficiency becomes especially important for the extended transients typically encountered for unprotected accidents.
In order to provide a more mechanistic approach to the calculation of the radial core expansion reactivity feedback, and to provide a framework for more detailed modeling as required, the following detailed model was developed. It is intended to overcome the restrictions associated with the assumptions listed above, and to allow a more appropriate use of results from detailed computer code simulations of core behavior, such as those obtained with NUBOW-3D [4-5].
4.5.6.2.1. Model Description¶
The approach taken in the development of the detailed model is to relate the reactivity feedback from radial core expansion to a change in the size of the core, in the same manner as a uniform dilation of the core is used to calculate the reactivity effect of a change in effective core radius. However, rather than maintain the cylindrical shape associated with a uniform core dilation, an axial profile of core radius is calculated. During a transient, the changes in the axial profile are used in conjunction with a worth curve for radial core expansion to yield the reactivity feedback.
The axial profile of the core radius is obtained from the behavior of an average subassembly in the outer row of the core. The shape of this subassembly is determined by the relative location of the grid plate, the core, the load pads, and any core restraint rings. The shape is also affected by the thermal gradient across the subassembly, as this introduces additional bending of the subassembly. The subassembly is treated as a continuous beam subject to these conditions and restraints. The basic equation that describes these deflections is the differential equation of the elastic curve of the beam,
(4.5‑26)
where
\(E\) = modulus of elasticity, N/m2
\(I\) = moment of inertia of the beam cross-sectional area, m4
\(M\) = bending moment, N-m
\(x\) = distance along the beam, m
\(y\) = distance perpendicular to the beam, m
This equation is solved subject to various loads and moments, depending on the state of the core. However, since only the displacement is needed, and the forces and moments are never evaluated, the solution is not dependent on the value of EI.
At present, the model is only applicable to the “limited free bow” type of restraint. For this type of restraint, there are load pads just above the top of the core (ACLP) and at the top of the subassembly (TLP). There is also a restraint ring (RR), or core former, around the core at the top load pad elevation. This restraint ring limits the outward motion of the top of the subassembly. With this type of restraint, the shape of the subassembly is determined by one of the following possibilities:
Grid Plate/Subassembly Nozzle Clearances Not Exceeded
A.1. No contact at ACLP, RR, or TLP
(4.5‑27a)
A.2. No contact at ACLP or TLP; contact at RR
(4.5‑27b)
A.3. No contact at ACLP or RR; contact at TLP
(4.5‑27c)
A.4. Contact at ACLP; no contact at TLP or RR
(4.5‑27d)
A.5. Contact at ACLP and RR; no contact at TLP
(4.5‑27e)
Grid Plate/Subassembly Nozzle Clearances Exceeded
B.1. No contact at ACLP; contact at RR
(4.5‑27f)
B.2. No Contact at ACLP or RR; contact at TLP
(4.5‑27g)
B.3. Contact at ACLP; no contact at TLP or RR
(4.5‑27h)
B.4. Contact at ACLP and RR; no contact at TLP
(4.5‑27i)
B.5. Contact at ACLP and TLP; no contact at RR
(4.5‑27j)
where
\(y\) = radial displacement with respect to the core radius at the grid plate
\(R_{1}\) = minimum core radius at the above-core load pad with respect to the core radius at the grid plate
\(R_{2}\) = minimum core radius at the top load pad with respect to the core radius at the grid plate
\(R_{3}\) = maximum core radius at the restraint ring with respect to the core radius at the grid plate
\(x\) = axial elevation
\(x_{1}\) = elevation of the lower axial blanket/lower reflector interface
\(a\) = elevation of the above core load pad
\(L\) = elevation of the top load pad
\(S_{\text{GR}}\) = subassembly slope with respect to vertical at the grid plate
\(S_{\text{GRMAX}}\) = maximum subassembly slope with respect to vertical at the grid plate
\(\frac{M_{1}}{\text{EI}}\) = thermally induced bending moment in the core region
\(\frac{M_{2}}{\text{EI}}\) = thermally induced bending moment in the above core region
\(V_{\text{GR}}\) = radial reaction at the grid plate
\(M_{\text{GR}}\) = applied moment at the grid plate
\(P\) = radial force at the above core load pad
\(\text{EI}\) = modulus of elasticity times the moment of inertia of the subassembly cross-sectional area
The use of the word contact in this context implies that either the outward motion is sufficient for the restraint ring to apply a force preventing further outward motion, or there is sufficient inward motion such that all of the intra-subassembly gaps in the load pad region(s) are eliminated, thus generating a force preventing further inward motion. A grid plate/subassembly nozzle clearance is required for the replacement of subassemblies, and results in a corresponding maximum possible deviation of the subassembly from vertical at the grid plate. When this clearance is exceeded, a moment is applied to the subassembly at the nozzle.
The subassembly is also subjected to a bending moment related to the temperature difference of opposite hex can walls within the subassembly. This temperature difference is converted into an equivalent bending moment, as described in the following section. The temperature difference increases linearly through the core region, from the lower axial blanket to the upper axial blanket. In the upper subassembly region, the temperature difference is assumed to be constant from the upper axial blanket to the top of the subassembly, with the value varying with time as the transient progresses.
The major assumptions incorporated in this model at present include the uniform distribution of core material in the radial direction at every axial elevation and the completely rigid subassembly load pads. Distributing the material uniformly at each axial elevation as the core radius changes is the same assumption used for the uniform core dilation calculation to obtain the radial core expansion reactivity feedback coefficient, and implies that all of the subassemblies are moving in proportion to their distance from the center of the core. The radial expansion worth gradient and the intra-subassembly temperature gradients tend to be greatest at the edge of the active core, with the result that most of the reactivity feedback effect comes from movement of the outer row of subassemblies. Any movement in the central region of the core that is not proportional to the distance from the center of the core is expected to cause a minor effect. The accuracy of this assumption for any specific reactor core can be evaluated by comparison with results from NUBOW-3D [4-5].
The use of completely rigid subassembly load pads provides slightly greater expansion of the core during certain events as in an unprotected loss-of-flow, and less for other accidents, such as an unprotected loss-of-heat-sink transient. The error introduced by using this assumption is on the order of 15% to 20%, and can be design dependent. The incorporation of deformable load pads and “bridging” of subassemblies may be desirable, and is being considered for a future version of this model. The accuracy of this assumption can also be checked by comparison with NUBOW-3D.
Since the expression given by Eq. 4.5-26 is solved for the various core loading possibilities listed above, the resulting algebraic formulas are incorporated in the code. This avoids the need for a finite difference solution of Eq. 4.5-26, simplifying the computer coding and providing a rapid calculation of the core shape.
4.5.6.2.2. Code Description and Input Requirements¶
This section contains a description of the algorithm used for calculating the appropriate core shape. This calculation is performed at the start of the transient to establish the steady-state core configuration, and for every step during the transient. The use of the detailed radial core expansion reactivity feedback model requires some of the same input as the simple model plus several other variables. These will be discussed as their use occurs.
The optional model is activated by setting
\(|\) IRADEX \(| =\) 4 or 5, where a value of ±5
gives a much more detailed printout, while ±4
only gives results in the PSHORT printout. The first step is to
calculate the average temperature of the above-core load pad (ACLP) and
top load pad (TLP) regions. This is done using Eq. 4.5-25, as in the
basic model. The model sets the location of the ACLP, so that JSTRDX does not need to be input. The temperature of the
grid plate can be given by either the inlet coolant temperature, or by
the wall temperature of the compressible volume used to represent the
inlet plenum in PRIMAR-4. This option is discussed in detail for the
basic model, and is activated by setting IRADEX to the
appropriate negative value.
The next step is to calculate the equivalent core radius at the grid plate, the ACLP and the TLP. For this calculation, the following input is needed:
Input |
Description |
|---|---|
total number of subassemblies in the active core region, including internal blankets and control subassemblies |
|
material used for the grid plate, where
|
|
|
|
material used for the ACLP and TLP, where
|
subassembly pitch at the grid plate at reference temperature |
|
flat-to-flat dimension across the ACLP at reference temperature |
|
flat-to-flat dimension across the TLP at reference temperature |
Using the pitch at the grid plate along with the steady-state inlet temperature, the equivalent radius of the subassemblies in active core is calculated. As part of the calculation, there is a call to subroutine THRMEX that gives the material thermal expansion as a function of temperature for either 316 SS or HT-9. For the load pad regions, a minimum allowable core radius is calculated based on the size of the load pad region when all of the load pads are pushed together and there are no intra-subassembly gaps. This is possible since the model assumes the load pads all have the same temperature, as described above.
In addition to these dimensions, there are two other geometric constraints, as follows:
Input |
Description |
|---|---|
maximum allowable slope of the subassembly at the grid plate with respect to vertical, based on subassembly nozzle/grid plate clearances and dimensions |
|
clearance between the top load pads and the restraint ring |
The value for SLLMAX is calculated from the radial clearances of the
subassembly nozzle/grid plate socket connection and the length of the
connection. The maximum tilt of the subassembly occurs when the maximum
radial motion of the nozzle is used, usually inward at the bottom of the
nozzle and outward at the top. This number is design-dependent and can
vary greatly, even when the subassembly sizes are comparable. The
clearance between the top load pad region and the restraint ring is
determined by the maximum clearance that would occur between the
subassemblies in the outer row of active core and the first row of
radial blankets when all of the core subassembly load pads are pushed
inward together and all of the radial blanket load pads are pushed
outward against the restraint ring. The top load pad/restraint ring
clearance is kept constant throughout the transient, i.e. the restraint
ring expands as the top load pads expand thermally. This approximation
tends to be conservative. Default values for these two input variables
have been provided for cases where such detailed design information is
not available. Design information should be used wherever possible, as
the results can be especially sensitive to the value for SLLMAX.
The only other input variable required for determining the core shape are those related to the thermally-induced bending moment:
Input |
Description |
|---|---|
applied bending moment at the top of the core region, representing the flat-to-flat temperature difference in the radial direction for the subassemblies at the outer edge of the active core |
|
applied bending moment in the region above the core, representing the flat-to-flat temperature difference in the radial direction in this region for the subassemblies at the outer edge of active core |
The data on the temperature difference must be obtained from a code which performs detailed calculations of the steady-state subassembly temperatures with intersubassembly heat transfer, such as SUPERENERGY-2 [4-6]. Default values are included if such information is not available. The input variables can then be calculated using Eq. 4.5-28.
(4.5‑28)
where
\(\alpha\) = mean thermal expansion coefficient of the subassembly hexcan, \(1/K\)
\(\Delta T\) = flat-to-flat temperature difference, K
\(D\) = hexcan flat-to-flat dimension, m
The model uses a linear variation in bending moment through the core
region, from zero at the bottom of the core to BNDMM1 at the top. The
bending moment BNDMM2 is applied uniformly from the top of the core to
the top of the subassembly. In the transient, the bending moments are
modified in proportion to the power-to-flow ratio changes.
Once all of these conditions have been calculated, the algorithm goes through a series of logic to determine the correct combination of forces and moments, as given above. The subassemblies are assumed to be vertical at the grid plate unless there are forces at the ACLP or TLP, or both, which would cause the subassembly to tilt. With the appropriate choice, the algebraic equation corresponding to that loading condition is evaluated for every axial node in the core region. In the printout, the algebraic equation selected is indicated by “CORE SHAPE MODEL =”, where the value printed corresponds to the particular case as listed:
CORE SHAPE MODEL
Steady-State |
Transient |
|
|---|---|---|
Grid plate/subassembly nozzle clearances not exceeded |
||
No contact at ACLP, RR or TLP |
1.0 |
21.0 |
No contact at ACLP; contact at RR |
2.0 |
22.0 |
No contact at ACLP; contact at TLP |
3.0 |
23.0 |
Contact at ACLP; no contact at TLP or RR |
4.0 |
24.0 |
Contact at ACLP and RR |
5.0 |
25.0 |
Grid plate/subassembly nozzle clearances exceeded |
||
No contact at ACLP; contact at RR |
8.0 |
28.0 |
No contact at ACLP; contact at TLP |
9.0 |
29.0 |
Contact at ACLP; no contact at TLP or RR |
10.0 |
30.0 |
Contact at ACLP and RR |
11.0 |
31.0 |
Contact at ACLP and TLP |
12.0 |
32.0 |
In the steady-state, the axial profile of core radius is stored for comparison during the transient. For each step during the transient, the process is repeated and the difference in core radius at each elevation is calculated.
The reactivity worth curve is based on the radial expansion coefficient for a uniform core dilation,
radial expansion coefficient for a uniform core dilation, $/m |
This coefficient is then proportioned among the axial fuel nodes according to the axial power shape. The resulting worth curve provides the radial displacement worth for each axial node in the core. When used in combination with the deflections from steady-state described above, the reactivity feedback from each axial node is determined and the total reactivity feedback from radial core expansion is calculated by summing over the axial fuel nodes. As stated above, this is a very rapid calculation due to the use of algebraic expressions for the subassembly shape, which are the solutions given in Eq. 4.5-27 for the various combinations of force and moments.
4.5.7. Control Rod Drive Expansion Feedback Reactivity¶
For the control rod drive feedback model, it is assumed that the control
rod drives are washed by the outlet coolant from the core. Thermal
expansion of the drives due to a rise in core outlet temperature will
cause the control rods to be inserted further into the core, providing a
negative reactivity component. On the other hand, if the control rod
drives are supported on the vessel head, and if the core is supported by
the vessel walls, then heating the vessel walls will either lower the
core or raise the control rod drive supports, leading to a positive
reactivity component. Both the control drive expansion and the vessel
wall expansion are accounted for in SAS4A/SASSYS‑1. This model is
invoked with input variable ICREXP.
A simple one-node treatment is used for calculating the temperature of the control rod drives. The equation used is
(4.5‑29)
where
\(M_{\text{cr}}\) = mass of the control rod drivelines, kg
\(C_{\text{cr}}\) = specific heat of the rod drivelines, J/kg-K
\(T_{\text{cr}}\) = control rod drive temperature, K
\(T_{\text{ui}}\) = coolant temperature in the upper internal structure region, K
\(h_{\text{cr}}\) = heat transfer coefficient between the coolant and the control rod drive, W/m2-K
\(A_{\text{cr}}\) = heat transfer area between the coolant and the control rod drive, \(\text{m}^2\)
\(t\) = time, s
The product of the control rod driveline mass and specific heat is
entered as input variable CRDMC, and the
product of the driveline heat transfer coefficient and area is entered
as CRDHA.
The coolant temperature in the upper internal structure region is calculated using
(4.5‑30)
where
\(w_{\text{c}}\) = core outlet flow rate
\(T_{\text{mm}}\) = mixed mean coolant outlet temperature
\(\rho_{\text{u}}\) = sodium density in the outlet plenum
\(V_{\text{ui}}\) = coolant volume in the upper internal structure region
Initially both \(T_{\text{ui}}\) and \(T_{\text{cr}}\) are set
equal to the steady-state mixed mean outlet temperature. The UIS volume,
\(V_{\text{ui}}\) is entered as input variable UIVOL.
During the transient calculation, Eq. 4.5-30 is approximated with
(4.5‑31)
where
(4.5‑32)
For this calculation, only channels with positive outlet flow rates contribute to \(w_{\text{c}}\) and \(T_{\text{mm}}\). Eq. 4.5-29 is approximated as
(4.5‑33)
or
(4.5‑34)
where
(4.5‑35)
The axial expansion of the control rod drive, \(\Delta z_{\text{cr}}\), is calculated as
(4.5‑36)
where \(L_{\text{cr}}\) is the length of the control rod drive
washed by the outlet sodium, and \(\alpha_{\text{cr}}\) is the
thermal expansion coefficient. These data are entered as CRDLEN and
CRDEXP.
The vessel wall expansion is calculated on the basis of the temperatures calculated by PRIMAR-4 for the walls of the liquid elements or compressible volumes that represent the vessel wall. For a typical pool reactor, the vessel wall would be the wall of the cold pool; but for some reactor designs a number of compressible volumes and liquid elements would be used to represent the vessel wall. The expansion of the vessel wall, \(\Delta z_{\text{v}}\), is calculated as
(4.5‑37)
where
\({\overline{T}}_{\text{k}}\) = average wall temperature of the k-th compressible volume or liquid element in the vessel wall
\(L_{\text{k}}\) = length of the vessel wall represented by the k-th compressible volume or element
\(\alpha_{\text{k}}\) = thermal expansion coefficient of the vessel wall
The net movement, \(\Delta z_{\text{n}}\), is calculated as
(4.5‑38)
and the reactivity feedback, \(\delta k_{\text{cr}}\), is calculated as
(4.5‑39)
where \(a_{\text{cr}}\) and \(b_{\text{cr}}\) are user-supplied
coefficients entered as ACRDEX and BCRDEX.
A multiple-node version of this model is in development, but has not been verified for production use.
4.5.8. Fuel and Cladding Relocation Feedback Reactivity¶
The fuel and cladding relocation reactivity feedbacks are calculated as
the product of the input material reactivity worth (CLADRA and FUELRA) and the change in the axial
material mass distribution since the initial steady-state condition.
Symbolically this is represented by
where \(\left( \frac{\Delta k}{\Delta m} \right)_{ij}\) is
the material reactivity worth in axial node \(j\) of channel
\(i\), \(m_{ij}\left( t \right)\) is the material mass at
axial node \(j\) in channel \(i\) at time \(t\), and
\(m_{ij}\left( 0 \right)\) is the initial steady-state node
material mass. The input worth curves may be input on the fuel (MZ)
mesh, or the coolant (MZC) mesh according to the input value of IREACZ.
The initial and transient axial mass
distributions are computed internally from input design geometry and
density data, and the fuel and cladding relocation models and solutions.
4.5.9. EBR-II Reactivity Feedback model¶
A reactor-specific set of reactivity feedback correlations has been implemented in SAS4A/SASSYS‑1 for analysis of the EBR-II reactor and plant. The formulation of these correlations is based on the reactivity feedback model used in the NATDEMO computer program [4-7, 4-8], which is based on analysis of reactivity temperature coefficients in EBR-II Run 93 [4-9]. This documentation of the SAS4A/SASSYS‑1 EBR-II reactivity feedback model is taken from notes provided by White [4-10] and Herzog [4-11].
In SAS4A/SASSYS‑1, the EBR-II reactivity feedback is assumed to be composed of nine components. These components are: 1) fuel expansion, 2) coolant expansion, 3) stainless steel expansion, 4) axial reflector sodium expansion, 5) radial reflector sodium expansion, 6) fuel Doppler effect, 7) control rod bank expansion, 8) upper grid plate expansion, and 9) core subassembly bowing.
Each of these effects will be considered independently and the method in which the feedback magnitude is determined will be given. The source and nature (linear or nonlinear) of the term will also be discussed.
The reactivity in a steady state critical reactor is defined as zero. In the EBR-II feedback calculation, a parameter, which shall be named \(\zeta\left( 0 \right)\), is defined at time zero (this treatment is not used in the other reactivity calculations performed by SAS4A/SASSYS‑1). At later times, \(\zeta\left( t \right)\) is calculated. The difference, \(\delta k \left( t \right) = \zeta\left( t \right) - \zeta\left( 0 \right)\), is the reactivity introduced from feedback effects at time \(t\).
4.5.9.1. Fuel Expansion¶
Both radial and axial expansion of the fuel are considered to be linear terms.
4.5.9.1.1. Axial Expansion¶
The method used is derived from Ref. 4-12. It has been modified to include the possibility that contact can occur between the fuel and cladding, thus altering the expression for the amount of expansion. Correlations from the Metallic Fuels Handbook [4-13] are used to evaluate the linear expansion coefficient and Young’s modulus for the fuel and cladding types used in EBR-II fuel elements. First, the following correlation is used to determine the coefficient of linear expansion for U-5FS fuel:
and for U-10Zr fuel, the following correlation is used:
and for U-10Zr-20Pu fuel, the following correlation is used:
The \(\overline{T}\) used here is the mass-average temperature for the fuel in a particular channel for a particular axial layer.
For SS316 or D-9 cladding, the steel linear thermal expansion coefficient is calculated from:
and for HT-9 cladding the linear thermal expansion coefficient is calculated from:
where \(\overline{T}\) is the mass-average cladding temperature at a particular axial location in a particular channel.
Correlations [4-13] for the Young’s modulus of metal fuels are functions
of the fuel temperature and porosity PRSTY. The following correlation is used to determine the Young’s
modulus of U-5Fs fuel:
For U-10Zr fuel, the following correlation is used:
And for U-10Zr-20 Pu fuel, the following correlation is used:
For SS316 or D-9 cladding, the steel Young’s modulus is calculated from:
and for HT-9 cladding the Young’s modulus is calculated from:
The expression for the expansion in the fuel is
for no contact (fuel burnup < 2.9%), and
for contact (fuel burnup > 2.9%), where \(\alpha_{\text{Lf}}\) and \(\alpha_{\text{Lss}}\) are the thermal expansion coefficients for the fuel and stainless steel, \(\Delta T_{\text{f}}\) and \(\Delta T_{\text{ss}}\) are the temperature changes for the fuel and stainless steel, \(Y_{\text{f}}\) and \(Y_{\text{ss}}\) are Young’s modulus for the fuel and stainless steel, and \(A_{\text{f}}\) and \(A_{\text{ss}}\) are the cross sectional areas of the fuel and stainless steel.
As described above, the change in temperature is not calculated directly by the code. Instead, the code expands the expression into two terms: one involving steady state conditions, \(\zeta\left( 0 \right)\), and the second involving the conditions at some time \(t\), \(\zeta\left( t \right)\). The reactivity feedback is determined using the expression \(\delta k \left( t \right) = \zeta\left( t \right) - \zeta\left( 0 \right)\). The parameter \(\zeta\) due to the expansion can be expressed as:
where \(\beta\) is the delayed neutron fraction, \(\zeta_{\text{fa}}\) is the reactivity due to fuel axial expansion in dollars, \(\left( \frac{\partial \text{k}}{\frac{\partial \text{N}}{N}} \right)_{\text{f}}\) is the change in \(k\) with a relative change in the number density of the fuel, and \(\left( \frac{\partial \text{k}}{\frac{\partial \text{H}}{H}} \right)_{\text{f}}\) is the change in \(k\) with a relative change in the height of the fuel, for the case when the clad and fuel are in contact and
for the case where there is no contact. The two partial derivatives in
both of these expressions are entered as input to SAS4A/SASSYS‑1 as
input variables YKNF and YKHF.
Because some channels will have both assemblies in which the cladding and fuel do contact and assemblies in which they do not contact, the code uses the equation:
where \(F_{\text{LowBU}}\) is the fraction of pins with < 2.9%
burnup. This fraction is entered to SAS4A/SASSYS‑1 as variable FLOWBU.
The temperature of the stainless steel (cladding) is determined using a weighted mass-average of the cladding temperature. The cladding is composed of three radial nodes. In the weighting, the middle node is given twice the weight of the two other nodes.
4.5.9.1.2. Radial Expansion¶
The radial expansion of the fuel contributes to the reactivity principally by displacing the bond gap sodium from the core. This displacement is of the sodium between the cladding and the fuel. Once the fuel reaches a burnup of 2.9% the cladding is in contact with the fuel and there is no additional displacement, and therefore, no additional reactivity change. The amount by which the fuel volume increases can be determined using a two dimensional isotropic approximation, i.e.: fuel volume increase is \(V_{\text{f}}{2\alpha}_{\text{Lf}}\). The fractional decrease in the sodium volume is then \(\frac{V_{\text{f}}2\alpha_{\text{Lf}}}{V_{{\text{Na}}}}\). The \(\zeta\) value associated with this sodium expulsion is:
when there is no contact and \(\zeta_{\text{fr}} = 0\) when there is
contact. In these expressions,
\(\left( \frac{\partial \text{k}}{\frac{\partial \text{N}}{N}} \right)_{{\text{Na}}}\) is
the change in \(k\) with respect to a relative change in the number
density of the sodium, which is entered as input variable YKNNA.
Therefore, the value of \(\zeta\) for the
radial expansion of the fuel can be expressed as:
The same type of summation as given above is used to volume weight the reactivities (and temperatures, \(\zeta\) values) from the different axial layers and channels.
4.5.9.2. Coolant Expansion¶
When the sodium coolant expands, it increases the leakage from the reactor, decreases sodium capture and results in spectral shifts. Sodium expansion is assumed to be a linear effect. The sodium coolant expansion is treated in a manner developed in Ref. 4.9. The equation used is:
where \({\alpha_{\text{V}}}_{{\text{Na}}}\) is the thermal volumetric expansion coefficient, \({\overline{T}}_{{\text{Na}}}\) is the sodium temperature, and the sodium temperature is the value assigned by the code for a particular channel and axial layer. The sodium volumetric thermal expansion coefficient is calculated from the local sodium temperature in the correlation for the sodium volumetric thermal expansion coefficient given in Eq. (12.13-10).
The reactivity worths are summed in the manner described in the fuel
axial expansion section. The sodium number density reactivity
coefficient is entered as YKNNA, the
radial sodium reactivity worth factor is entered as XRNSHP, and the axial sodium reactivity worth weighting is
taken as the normalized axial shape of VOIDRA.
4.5.9.3. Stainless Steel Expansion¶
Both axial and radial steel expansion coefficients are considered to be linear effects.
4.5.9.3.1. Axial Expansion¶
The axial expansion of the stainless steel cladding results in a decrease in the number density. The amount of expansion, as in the case of the fuel, is different for conditions where there is contact or no contact. In the event of no contact (burnup < 2.9%), the expression for the reactivity is:
where \(\alpha_{\text{Lss}}\) is the linear thermal expansion coefficient for the cladding, and \(\left( \frac{\partial \text{k}}{\frac{\partial \text{N}}{N}} \right)_{{\text{ss}}}\) is the change in \(k\) with respect to the relative number density in the stainless steel.
The partial derivative above is an input parameter, YKNSS.
If there is contact, the following expression applies:
The code therefore contains the expression:
The radial and axial weighting of the steel expansion reactivity is
carried out in the same manner as for the fuel expansion reactivity. The
radial steel reactivity worth shape factor is entered as XRSSHP,
and the axial shape is taken as the normalized
axial shape of input array CLADRA.
4.5.9.3.2. Radial Expansion¶
The reactivity feedback due to radial expansion of the cladding results from the displacement of sodium from the core. This removal is independent of the burnup because the expansion is directed toward the coolant channel. The expression for the radial expansion of the stainless steel structure is:
where \(V_{\text{ss}}\) is the volume of stainless steel in the cladding, and \(\zeta_{\text{ssr}}\) is the reactivity feedback due to radial expansion of the clad.
The same type of summation as given above (Section 4.5.9.3.1) is used to volume weight the reactivities.
4.5.9.4. Axial Reflector Sodium Expansion¶
In the axial reflector the reactivity feedbacks stem mostly from the change in leakage. The upper and lower axial reflector sodium expansion are treated as linear effects.
4.5.9.4.1. Upper Reflector¶
The expression for the upper reflector sodium parameter \(\zeta\) is:
where \({\overline{T}}_{\text{ur}}\) is the average temperature in the upper reflector, and \(\left( \frac{\partial \text{k}}{\partial \text{T}} \right)_{\text{ar}}\) is the change in \(k\) with respect to a change in axial reflector temperature.
The input value for the above partial derivative is entered as variable
YRCUR.
To determine the average temperature of the coolant in the upper reflector, the following equation is used:
where \(N\) is the number of axial nodes in the gas plenum, \(M\) is the number of zones in the upper reflector, \(L\left( j \right)\) is the number of axial nodes in zone \(j\). Also, \(V_{\text{i}}\) is the volume of coolant node \(i\) in the plenum space, \(T_{\text{i}}\) is the temperature of the node \(i\) coolant in the plenum space, \(V_{\text{j,k}}\) is the volume of coolant node \(k\) in zone \(j\) in the reflector area, and \(T_{\text{j,k}}\) is the temperature of the coolant in node \(k\) of zone \(j\) in the reflector area.
In this analysis, only the sodium coolant is considered to determine the reactivity feedback. This is done for two reasons: the difference between the sodium coolant and stainless steel temperature is small and the relative contributions of the stainless steel and coolant expansions are unknown. The volumes used are that of the flow, not of the structure and flow.
4.5.9.4.2. Lower Reflector¶
The expression for the lower reflector sodium feedback is:
where the partial derivative is entered as input variable YLCLR and
\({\overline{T}}_{\text{lr}}\) is the average
temperature in the lower reflector.
The same temperature volume-weighting scheme used in the upper reflector is also used in the lower reflector. Again, the temperatures are that of the coolant and the volumes are that in which flow occurs.
4.5.9.5. Radial Reflector Expansion¶
The reactivity change that results from a temperature change in the radial reflector is mainly due to the change in density of the sodium in the reflector, which results in a change in the leakage. The radial reflector expansion is treated as a linear effect. The expression for the radial reflector sodium feedback is:
where \(\left( \frac{\delta \text{k}}{\delta \text{T}} \right)_{\text{rr}}\) is the change in \(k\) with respect to the radial reflector temperature, and \({\overline{T}}_{\text{rr}}\) is the average temperature of the radial reflector.
The partial derivative is entered as input variable YRCRR.
The nodes from which the average temperature is
determined are those in which LCHTYP is set to 2, indicating a stainless
steel reflector subassembly, and those of the bypass region at the core
level. For the channel subassemblies, only zone 5 (currently the core)
is used in the volume weighting. For the bypass channel, the
temperatures are also volume weighted. The coolant temperature is volume
weighted in all axial nodes of all channels to obtain the average
temperature. The equation used in the code is:
where \(V_{\text{by,i}}\) is the volume of bypass region \(i\), \(T_{\text{by,i}}\) is the temperature of the bypass region \(i\), \(V_{\text{by}}\) is the total volume of the bypass region corresponding to the reflector, \(V_{\text{ch,j}}\) is the volume of axial layer \(j\) of the stainless steel containing channel, \(T_{\text{ch,j}}\) is the temperature of axial layer \(j\) of the stainless steel containing channel, \(V_{\text{ch}}\) is the total volume of the stainless steel channel.
4.5.9.6. Doppler Effect¶
The Doppler effect is a nonlinear phenomenon that results from the change in effective cross sections at different temperatures. The temperature coefficient for the Doppler effect \(\left( \frac{\delta \text{k}}{\delta \text{T}} \right)_{\text{D}}\) is a function of fuel temperature:
where \(k_{\text{D}}\) is an input variable YRCDOP and \({\overline{T}}_{\text{f}}\) is the channel
average fuel temperature. Since the Doppler temperature coefficient is
temperature dependent, an average value is used.
where \({\overline{T}}_{\text{f}}\left( t \right)\) is the channel average fuel temperature at time \(t\), and \({\overline{T}}_{\text{f}}\left( 0 \right)\) is the steady-state channel average fuel temperature.
The total feedback \(\delta k_{\text{D}}\) due to the Doppler effect is the sum of the Doppler feedbacks for each fueled channel. This is implemented in the code as:
where the temperatures given above are currently weighted by the axial and radial reactivity worths.
4.5.9.7. Control Rod Bank Expansions¶
The change in reactivity that results from control rod bank temperature change is a result of the support of these rods. These are suspended from the top of the reactor. When a temperature change occurs, the rods expand or contract, forcing some of the fuel into or out of the core. This results in a reactivity change. The control rod expansion is treated as a linear effect. Although there are several portions of the control rod that undergo expansion when the temperature is increased, the current code only models two. The first of these is the control rod fuel and the second is the driveline expansion. The expression found in the code is:
where \(T_{\text{CV}2}\) is the temperature in the upper plenum (CV#2 in SAS4A/SASSYS‑1), \(\left( \frac{\delta \text{k}}{\delta \text{T}} \right)_{\text{cr}}\) is the change is the change in \(k\) with respect to control rod temperature, and \(F_{\text{cr}}\) is the fraction of the response due to the channel temperature change.
The partial derivative above is entered as input variable YRCCR and
\(F_{\text{cr}}\) is entered as FCR.
The model given above differs from previous models [Ref. 4-12] because it does not include different time constants which characterize the different portions of the stainless steel control rod structure; instead, they are treated as the two terms given above; one proportional to fuel temperature and the other proportional to the exit plenum temperature. For steady state or a series of steady states this will not result in any significant error.
4.5.9.8. Upper Grid Plate Expansion¶
The upper grid plate is located below the core and serves as a support for the hex can. Grid plate expansion impacts the reactivity by displacing the assembly rows in the reactor. The upper grid plate expansion is treated as a linear effect. Reference 4-9 gives the following expression for the feedback:
where \(\zeta_{\text{gp}}\) is the reactivity due to the upper grid plate expansion, \(T_{\mathrm{CV1}}\left( t \right)\) is the temperature of the inlet plenum (CV#1 in SAS4A/SASSYS‑1), and \(\left( \frac{\delta \text{k}}{\delta \text{T}} \right)_{\text{gp}}\) is the feedback coefficient associated with the grid plate.
The partial derivative above is an input parameter entered as YRCGP.
4.5.9.9. Bowing and Unspecified Parameters¶
In the EBR-II reactivity feedback model, “bowing” is a “catch all” for terms which can not specifically be identified and therefore may contain terms other than that which result from the bowing of the assembly. True assembly bowing results when one side of a fuel assembly is at a higher temperature than the other. This results in a different expansion of the two sides moving the assembly radially. Bowing contributes to the reactivity by increasing or decreasing the amount of fuel in relatively high worth portions of the core.
The overall “bowing” term in the EBR-II model is treated as a linear
effect that is modeled by one line below a threshold and by another line
above the threshold. The effect is a function of the normalized
temperature rise across the core
\(\Delta T_{{\text{norm}}}\). For normalized temperatures
above the threshold, which is given by the input variable YTCUT, the bowing reactivity
\(\delta k_{\text{bw}}\) is given by:
For normalized temperatures below the threshold, the bowing reactivity \(\delta k_{\text{bw}}\) is given by:
The values for the input coefficients \(A\) and \(B\) are
entered as YABOW and YBBOW.
The normalized temperature rise is the ratio of the temperature rise
across the core at time t to the temperature rise across the core at
full power and flow conditions. The temperature rise is modeled as the
difference between the upper and lower plena temperatures (found in
YTLCV2 and YTLCV1) or as the difference between the average sodium
temperature for the fueled channels
\({\overline{T}}_{{\text{Na}}}\) and the
temperature of the lower plenum YTLCV1. Which model is used for the
normalized temperature rise is determined by an input parameter IBOWTP.
For IBOWTP equal to zero, the normalized
temperature rise is based on the outlet and inlet plena temperatures. In
the case, the normalized factor YDELT0
gives the difference between the outlet and inlet plena temperatures at
full power and flow conditions. For IBOWTP not equal to zero, the
normalized temperature rise is based on the average sodium temperature
in fueled channels and the temperature of the inlet plenum. In this
case, the normalized factor YDELT0 gives the difference between the
average sodium temperature in the fueled channels and the temperature of
the inlet plenum at full power and flow conditions.