8.3. Fuel-pin Phenomenology¶
In addition to the area of investigation termed “mechanics” that was described in Section 8.2, there is another area which is broadly termed “phenomenology”. This includes those elements of fuel performance that are not necessarily considered in a structural/mechanical sense, but are generally of a microscopic nature resulting in macroscopic effects. Examples would include as‑fabricated porosity migration, grain growth, fission‑gas generation and release, and fuel swelling induced by solid and volatile fission products. Since these produce effects on various time scales, some are not considered in the transient calculation. However, all models have been coded so that they could be incorporated in the transient calculation if appropriate.
8.3.1. As-Fabricated Porosity Migration¶
When cylindrical oxide fuel pins are placed in a neutron flux, the volumetric heating rates and low thermal conductivity of the fuel combine to produce high temperatures and very steep radial thermal gradients. These conditions can lead to the phenomenon commonly referred to as restructuring. The most distinct macroscopic aspects are divided into the columnar, equiaxed, and as‑fabricated fuel zones. The basic physical processes that produce these zones have been identified as grain growth kinetics for the equiaxed zone, and porosity migration for the columnar zone. In this section, the phenomenon of porosity migration will be discussed.
Sintered fuel pellets contain residual pores on the grain boundaries. At the high temperatures commonly experienced in a nuclear fuel pin, the mobility of the constituent atoms can become important since this activity is usually related to the internal energy, which is represented in an Arrhenius equation form. However, if the temperature was uniform, there would be no macroscopic movement because there is no driving force. The large thermal gradients that exist in a fuel pin act as the driving force for atomic movement. This mobility and driving force cause the pores to migrate up the thermal gradient. This movement of porosity is important because the thermal conductivity of the fuel depends on its local porosity. If there is a large amount of pore migration a central hole will be formed. This change in geometry affects the heat transfer characteristics of the pin.
The process begins with the coalescence of the irregularly shaped pores in the as‑fabricated fuel. The coalescence and movement of these pores results in the formation of characteristic lenticular pores, with a long axis parallel to the fuel isotherms and the short axis in the direction of the thermal gradient. This initial step of becoming lenticular is not included in DEFORM‑4; only the movement of the pores up the thermal gradient.
There are three mechanisms that could lead to pore motion: (1) evaporation condensation across the pore, (2) pore surface diffusion, and (3) mass diffusion around the pores. The mass diffusion process is assumed to be negligible because of the high activation energy required to make atoms in a solid sufficiently mobile to produce appreciable mass transport. The evaporation‑condensation process is expected to be the dominant process if the as‑fabricated pores are large and temperatures are high. If the pores are small and at lower temperatures, the surface diffusion process would be expected to dominate. When the LIFE‑III [8‑5] code was in the process of thermal calibration, it was found that the available data made it impossible to determine the thermal dependences of these last two processes, so the evaporation-condensation process was chosen as the dominant mechanism. This same approach has been employed in DEFORM‑4.
The large radial thermal gradient existing in reactor fuel pins at power produces a gradient across the pore. The atoms on the hotter surface evaporate, move across the pore, and condense on the cooler surface. This causes the pore to move up the thermal gradient. Bober and Schumacher [8‑6] developed the following form for the velocity of the pore due to this process.
(8.3‑1)
where
\(U\) = Pore velocity, m/s
\(T\) = Temperature, K
\(r\) = Radius, m
\(A_{\text{p}}\) = Pre-exponential factor, m2 T(A-1) s-1
\(Q_{\text{p}}\) = Evaporation-condensation activation energy, J g-mole-1
\(R\) = Universal gas constant, J K-1 g-mole-1
\(A\) = Temperature exponent
Theoretical values for \(Q_{\text{p}}\), \(A_{\text{p}}\), and \(A\) were obtained by Clement [8‑7] and compare well with experimental values. Values have also been determined through the thermal calibration of the LIFE‑III code [8‑5].
In a cylindrical fuel rod with an axisymmetric power distribution, the thermal gradient is zero at the center of the pin, or inner surface if a central void exists. The direct application of Eq. 8.3-1 would result in an accumulation of porosity in the innermost cell. To avoid this nonphysical situation, the thermal gradient at the inner fuel cell boundary is assumed to be the average value across the central cell. This treatment simulates the diffusion of the pores and the formation of channels open to the central void.
In DEFORM‑4, each fuel cell is assumed to have a uniform porosity. The change in cell porosity is determined from the initial porosity, the porosity moving into the cell from a neighboring cell, and the porosity moving out of the cell to a neighboring cell.
(8.3‑2)
where
\(P_{\text{i}} \left( t + \Delta t \right)\) = Porosity in cell \(i\) at the end of the time step
\(P_{\text{i}} \left( t \right)\) = Porosity in cell \(i\) at the beginning of the time step
\(P_{\text{in}}\left( \Delta t \right)\) = Porosity moving into cell \(i\) from cell \(i + 1\)
\(P_{\text{out}}\left( \Delta t \right)\) = Porosity moving out of cell \(i\) and entering cell \(i-1\)
\(\Delta t\) = Time-step length
Lackey, et al. [8‑8] developed the amount of porosity crossing a cell boundary, based on the velocity of the pores and the length of the time step. The porosity in the annulus from \(r_{\text{i}}\) to \(r_{\text{i}} + U_{\text{i}} \Delta t\) would be expected to cross the cell boundary at \(r_{\text{i}}\) during the time step, \(\Delta t\). These considerations result in the following definitions for \(P_{\text{in}}\) and \(P_{\text{out}}\).
(8.3‑3)
(8.3‑4)
where
\(P_{\text{i} + 1} \left( t \right), P_{\text{i}} \left( t \right)\) = Initial porosity in fuel cells \(i+1\) and \(i\), respectively
\(r_{\text{i} + 1}\), \(r_{\text{i}}\) = Outer and inner radial boundaries of fuel cell \(i\)
\(U_{\text{i} + 1}\), \(U_{\text{i}}\) = Pore velocity at radial locations \(r_{\text{i}+1}\) and \(r_{\text{i}}\), respectively
\(A_{\text{i} + 1}\), \(A_{\text{i}}\) = Cross-sectional area of radial fuel cells \(i+1\) and \(i\), respectively
The application of Eqs. 8.3-2 through 8.3-4 could lead to a situation in which more porosity leaves a cell than exists originally and enters from the neighboring cell. This is clearly a nonphysical result of the equations. It is also unlikely that the porosity in any cell would become zero because porosity can become trapped behind dislocations, impurities, and fission products. A parameter, PRSMIN, is available to allow input of the minimum porosity allowed in a cell. If application of Eq. 8.3-2 would cause the new cell porosity to fall below PRSMIN, \(P_{\text{out}}\) is reduced to the amount, which would make the cell porosity equal to the allowed minimum. This treatment assumes that the total porosity is conserved.
At the fuel surface, the influx of porosity is assumed to be zero. Because of the strong temperature dependence of the Arrhenius term in Eq. 8.3-1, the pore velocity is very small even with the thermal gradient at its maximum. This, combined with the surface tension, makes it extremely unlikely to have significant porosity introduced at the fuel surface.
The above equations are solved in the subroutine PORMIG. In the solution, it is assumed that all pores in the vicinity of the boundary \(r_{\text{i}}\) travel at the velocity \(U_{\text{i}}\). Therefore, the maximum travel of a pore is directly related to the time‑step length.
(8.3‑5)
where
\(\Delta r_{\text{v}}\) = Maximum distance traveled by pores
In order to maintain accuracy, it has been found that the time step length should be restricted so that the maximum distance traveled by the fastest pores is less than a fourth of the cell width.
(8.3‑6)
where
\(\Delta t_{\text{m}}\) = Maximum time-step length
\(\Delta r_{\text{m}}\) = Extent of the fuel cell outside the fastest velocity boundary
\(U_{\text{m}}\) = Maximum pore velocity
There is a second reason for limiting the size of the computational time step. As discussed in Section 8.1.2, the thermal hydraulic calculations in SAS4A are performed separately from the mechanical/phenomenological calculations in DEFORM‑4. Since porosity migration changes the geometry of the fuel pin and the radial porosity distribution, which changes the conductivities, it is necessary to limit the time step so the geometric and property changes can be fed back into the thermal calculation. It has been found that the criterion given in Eq. 8.3-6 is quite adequate for this purpose.
When the porosity migrates up the thermal gradient, it can pull the grain boundaries along with it, producing the characteristic columnar grains seen in restructured fuel. If enough porosity has migrated out of a cell, the grains in the cell are assumed to be columnar. In DEFORM‑4, the mechanism for determining if a cell contains columnar grains is the checking of the current porosity against the initial value in the as‑fabricated fuel.
(8.3‑7)
where
\(R_{\text{eq}}\) = Fraction, input parameter
\(P_{\text{o}}\) = Initial as-fabricated porosity
If the inequality in Eq. 8.3-7 is satisfied, the cell is assumed to contain columnar grains. All cells inside the outermost cell that satisfy the inequality are also assumed to be columnar. This determination does not affect any calculations, but is used for comparisons with the results from the destructive examination of pins used in calibration exercises.
The movement of these as‑fabricated pores causes a movement of gas to the central void, and release to the plenum. In order to achieve a strict conservation of gases within the pin, the effect must be considered. At the as‑fabricated conditions, the porosity is assumed to contain helium in equilibrium with the reference conditions. This, therefore, defines the amount of gas associated with each radial cell. As the porosity changes in the cell, the associated gas is also changed under the assumption that the gas content change is directly related to the porosity change.
(8.3‑8)
where
\(G_{\text{af,i}} \left( t + At \right)\) = As-fabricated gas in radial cell \(i\) at end of the time step, kg
\(G_{\text{af,i}} \left( t \right)\) = As-fabricated gas in radial cell \(i\) at end of the time step, kg
Once the changes have been determined for all radial cells, the amount of gas released to the central void, and hence the plenum, is determined and added to the total helium inventory.
While this gas accountability may have a very small effect on the actual plenum pressure during the pretransient calculations, it can be significant under transient conditions. Since melting of a radial cell is assumed to release the as‑fabricated porosity and its associated gas into the molten cavity immediately, there can arise situations where this addition can affect the molten cavity pressure. With the conservation of this material considered in DEFORM‑4, a better representation of the molten cavity pressurization is provided, no matter the transient under study.
8.3.2. Grain Growth¶
At the relatively low temperatures in the outer fuel region, the as-fabricated porosity is unable to migrate despite the large thermal gradient, because the atomic mobility is too low. However, the atoms may be active enough to cross the grain boundaries. The larger grains grow at the expense of the smaller, due to the tendency of atoms to jump from a convex (higher energy) to a concave (lower energy) surface. The net effect is to reduce the surface area, and thereby, the surface energy associated with the grains. This grain growth is a strong function of atomic activity, i.e., temperature. In nuclear fuels, the surface temperature is usually below the “threshold” temperature where activity is great enough to cause redistribution at the grain surfaces. Due to the strong temperature dependence and the steep thermal gradient, a distinct region usually develops where the grains grow isotropically, irrespective of the large gradient. This “equiaxed” zone extends inward to the region where pore migration becomes active and produces the “columnar” grains by dragging the boundaries during migration.
The grain‑size distribution is important because the fission‑gas release and fuel‑creep functions depend on this parameter. The calculation of this clearly visible zone also offers a simple experimental calibration region, which can be used in the validation process.
Two grain‑growth models are available in the GRGROW subroutines and are selected through the input variable NGRAIN. If NGRAIN is greater than 0, the unlimited grain‑growth option is used and the value of NGRAIN is the grain diameter exponent; see Section 8.3.2.1 below. If NGRAIN is zero, a limited grain‑growth model is used. In this model the grain sizes are limited to an experimentally determined value; see Section 8.3.3.2 below. Both models give very similar results in the lower temperature regions associated with the equiaxed region where the grains are usually two to ten times the initial size. At higher temperatures, the first model results in larger grains because of the unconstrained growth. However, in these regions, porosity migration also produces the columnar grain structure which uses a separate method for determining the effective grain size for use in the fission‑gas release and fuel‑creep calculations; see Section 8.3.2.3 below. Because the unlimited growth model offers more flexibility to model mechanistic behavior, it is suggested for use prior to the validation of the integral code.
8.3.2.1. Unlimited Grain Growth - Equiaxed Region¶
The growth phenomenon may be characterized by a simple kinetic equation, with the growth rate given as
(8.3‑9)
where
\(D\) = Grain diameter, m
\(n\) = Growth mechanism input parameter
\(A_{\text{g}}\) = Pre-exponential constant
\(Q_{\text{v}}\) = Activation energy for the growth mechanism related to n, J g‑mole-1
\(t\) = Time, s
\(R\) = Universal gas constant, J K-1 g-mole-1
\(T\) = Temperature, K
The value of the parameter \(n\) is related to the grain-growth mechanism and depends on the driving and retarding forces being considered. Nichols [8‑9] developed theoretical meanings for the values usually associated with \(n\). If the grain boundaries are assumed to move toward their center of curvature at a rate proportional to the curvature, \(n\) would be 2. If the mechanism is through the evaporation‑condensation process across pores on the boundaries, with the pressure in the pores inversely proportional to their radius, the value of \(n\) is 3. If boundaries are shifted by volume diffusion moving material around the pores or the evaporation‑condensation process with the internal pore pressure constant, the value of \(n\) is 4. If the mechanism is surface or interface diffusion in the pores, the value of \(n\) is 5. In all cases where \(n\) is 3 through 5, it is assumed that the pores remain on the grain boundaries.
If the temperature is assumed constant for a time period \(\Delta t\), Eq. 8.3-9 can be integrated to yield
(8.3‑10)
The term (\(n A_{\text{g}}\)) is usually combined when determining the constants by comparison with experimental data, so Eq. 8.3-10 is rewritten as
(8.3‑11)
which is in the form coded in the GRGROW subroutine. In all cases, the values for the parameters \(G_{\text{k}}\) and \(Q_{\text{v}}\) depend strongly on the value of n used in Eq. 8.3-11.
R.N. Singh [8‑10] conducted an investigation into the grain‑growth kinetics for sintered UO2 pellets at temperatures between 1800 and 2100°C. His conclusions suggested that the cubic form of Eq. 8.3-10 was most accurate, and appropriate constants were determined. When the MATPRO‑10 [8‑11] materials properties package was developed, the available experimental evidence was collected, and curve fits were applied for exponents of 2 through 4. In this study, it was found that an exponent of 4 gave the best fit with 3 giving very similar results. In the GRGROW subroutine, the input variables for the exponent, pre‑exponential constant, and activation energy are used to provide maximum flexibility for the user.
8.3.2.2. Limited Grain Growth - Equiaxed Region¶
In a study of grain sizes in irradiated fuel by Ainscough, et al. [8‑12], a kinetics equation for grain growth was developed that included a maximum grain size. As the grains grow, the boundaries are retarded by the effects of intergranular pores, solid fission products, and gas bubbles. After the grains reach a certain size, they are stopped from additional growth. It was postulated that the maximum grain size could be represented by the form
(8.3‑12)
where
\(D_{\text{m}}\) = Maximum grain size, m
\(G_{\text{m}}\) = Pre-exponential constant, m
\(Q_{\text{m}}\) = Maximum grain size activation energy, J (g-mole)-1
\(R\) = Universal gas constant, J k-1 g-mole-1
\(T\) = Temperature, K
The temperature dependence of Eq. 8.3-12 results from the higher mobility of the retardants and the resultant reduction in grain‑boundary drag as the temperature increases.
The kinetic equation developed is then given by
(8.3‑13)
where
\(D\) = Grain diameter, m
\(G\) = Pre-exponential grain growth constant, m2 s-1
\(Q\) = Grain-growth activation energy, J g-mole-1
If the temperature is assumed to be constant over the time step, \(\Delta t\), the integration of Eq. 8.3-13 produces the following transcendental equation:
(8.3‑14)
The solution for \(D \left( t + \Delta t \right)\) is obtained through the Newton’s Method iterative scheme.
(8.3‑15)
where
\(D_{\text{k}}\) = The \(k\)-th estimate of the grain diameter to satisfy Eq. 8.3-14, m
(8.3‑16)
Since the grain size at the beginning of the time step, \(D \left( t \right)\), and the maximum grain size, \(D_{\text{m}}\), are known constants, the differentiation in Eq. 8.3-16 may be performed on Eq. 8.3-14 after expanding the log term to the difference of two 1og terms:
(8.3‑17)
Equation 8.3-17 is reduced to
(8.3‑18)
and this is substituted into Eq. 8.3-15 to produce the final form for the next estimate, \(k + 1\), of the grain size to satisfy Eq. 8.3-14.
(8.3‑19)
This iteration is continued until a consistent value is determined.
If the maximum grain size, \(D_{\text{m}}\), is smaller than the size at the beginning of the time step, \(D \left( t \right)\), due to power or temperature reductions, the current grain size, \(D \left( t + \Delta t \right)\), is maintained at its previous value.
8.3.2.3. Columnar Grain Size and Region Boundaries¶
The extent of the columnar region boundary is found as was discussed in Section 8.3.1. The effective grain size in this region is determined by the equiaxed grain size at the columnar/equiaxed boundary and the extent of the columnar boundary.
(8.3‑20)
where
\(D_{\text{co}1}\) = Effective grain size in the columnar region, m
\(\Delta r_{\text{co}1}\) = Radial extent of the columnar region, m
\(D_{\text{b}}\) = Equiaxed grain size at the columnar/equiaxed boundary, m
The boundary between the equiaxed and as‑fabricated region is based on the amount of grain growth. The grain size in each radial cell is compared to the initial grain size and if suitable growth has occurred, the region is classified as equiaxed.
(8.3‑21)
where
\(D_{\text{i}} \left( t + At \right)\) = Grain size in radial cell \(i\) at the end of the time step, m
\(R_{\text{ueq}}\) = Input factor
\(D_{\text{O}}\) = As-fabricated grain size, m
The check is started at the outer fuel surface and once the inequality in Eq. 8.3-21 is satisfied, that determines the equiaxed/as‑fabricated boundary.
8.3.3. Fission-gas Release¶
The nuclear fission processes occurring in the fuel during the irradiation produce both solid and gaseous fission products. The gaseous products are primarily xenon and krypton. The model currently used in DEFORM‑4 assumes that the gaseous products either precipitate as gas‑filled bubbles on the grain boundaries, are contained in microbubbles within the fuel matrix, or are released to the available free volume in the pin plenum and fuel central void. Formation of grain boundary bubbles leads to fuel swelling and reduces the fuel‑cladding gap size. The intra‑granular gas is assumed to play no part in fuel swelling but becomes important upon fuel melting. Release to the free volume changes the gas mixture and reduces the thermal conductivity of the gas in the gap. Fission‑gas release, fuel swelling, and the fuel‑pin temperature distribution are therefore closely interrelated. The migration of fission‑gas bubbles up the thermal gradient is not treated.
Fission gases can be released when they reach any open porosity such as cracks, the fuel‑cladding gap, the central void, or the fission‑gas plenum. At temperatures below about 1300 K, the mobility of the gas atoms is too low for diffusion, so they are released only by collisions with fission fragments near the fuel surface. This fraction is very small and can be neglected. At temperatures between about 1300 and 1900 K, the atomic motion is high enough to allow diffusion to the grain surfaces. At temperatures above 1900 K, the gas bubbles become mobile and may escape by migration up the temperature gradient.
The mechanistic approach to the problem of gas release has been employed in codes such as GRASS‑SST [8‑13] and FRAS [8‑14]. A complete modeling of the fission‑gas behavior is attempted in these codes, describing the migration and coalescence of fission‑gas bubbles in the grain and on grain boundaries. Gas release from the grains and grain boundaries to the exterior of the fuel are modeled. Detailed bubble‑size distributions are calculated and grain‑boundary channel formation is treated. The parameters involved have been studied and extensively calibrated.
Such a complete and detailed modeling effort is not currently envisioned for SAS4A. Because of the requirements that the SAS4A code size and running time be minimized, considerably simpler, less‑mechanistic models have been incorporated into SAS4A. These models relate the release rate to escape probabilities. These probabilities are modeled as functions of temperature and density. They should also be related to grain size, but are not in the current version. The calculations are performed in the subroutine RELGAS.
8.3.3.1. Fission-gas Generation¶
The total amount of fission gas generated in a fuel cell is related to the power of that cell. As the fission process proceeds, a number of isotopes result. Some of these fission products are volatile gases, which may coalesce to form fission‑gas bubbles. It is assumed that each fission produces a constant fraction of fission‑gas atoms.
(8.3‑22)
where
\(G_{\text{a}}\) = Number of gas atoms generated
\(F\) = Number of fissions during the time step
\(f_{\text{g}}\) = Fractional gas atoms generated per fission
While this model is not true of a single fission event, it does accurately represent the macroscopic results of a large number of fissions.
The number of fissions in an axial segment is related to the power generated.
(8.3‑23)
where
\(P_{\text{j}}\) = Power generated by axial fuel segment \(j\), \(w\)
\(\Delta t\) = Time-step length, \(s\)
\(E_{\text{f}}\) = Energy generated per fission, MeV
The numeric constant in Eq. 8.3-23 is the conversion factor from MeV to W-s. The code uses the amount of gas in units of mass, so Eq. 8.3-22 is rewritten as
(8.3‑24)
where
\(G_{\text{m}}\) = Mass of fission gas, kg
\(MW_{\text{fg}}\) = Molecular weight of the fission gas, amu
\(N_{\text{a}}\) = Avogadro number, \(0.6025 \times 10^{24}\) atoms/g-mole
The numeric constant in Eq. 8.3-24 converts g to kg. Combining Eq. 8.3-24 with 8.3-23 results in the mass of fission gas generated in the axial segment during the time step.
(8.3‑25)
If the radial power shape was flat, the total fission‑gas mass could be divided between the radial fuel cells on the basis of cell mass. However, it is possible to have a radial power shape. The fission‑gas mass in a radial fuel cell is determined by multiplying the fission gas generated by the whole segment by a radial factor.
(8.3‑26)
where
\(G_{\text{i}}\) = Fission-gas mass generated in radial fuel cell \(i\), kg
\(f_{\text{i}}\) = Fraction of total mass generated in radial cell \(i\)
The radial factor is based on the radial power shape factors and the radial fuel cell masses.
(8.3‑27)
where
\(S_{\text{i}}\) = Radial power shape factor for radial cell \(i\)
\(M_{\text{i}}\) = Fuel mass in radial cell \(i\), kg
\(N\) = Number of radial fuel cells
Substituting Eqs. 8.3-27 and 8.3-25 into Eq. 8.3-26 results in the fission‑gas mass generated in the radial cell.
(8.3‑28)
The amount of this gas located on the grain boundaries vs the amount retained in the fuel matrix is controlled through the input parameter FIFNGB. At each time step the new gas generated is divided between these two 1ocations
(8.3‑29)
(8.3‑30)
where
\(G_{\text{gb,i}}\) = Mass of generated fission gas assumed to be on grain boundaries in radial cell \(i\), kg
\(G_{\text{fm,i}}\) = Mass of generated fission gas assumed to be in the fuel matrix in radial cell \(i\), kg
\(f_{\text{gb}}\) = Fraction of fission gas generated that is on the grain boundaries, input parameter FIFNGB
Currently, release from these two regions is treated in the same manner, as described below. However, with this type of split in DEFORM‑4, it would be possible to develop different release mechanisms, and even provide for a radially dependent value of \(f_{\text{gb}}\). These considerations have been identified for possible future work if their effects were to become important.
This split in the gas location is significant because of the interactions with two other models: (1) the molten cavity pressure (Section 8.3.7), and (2) fission gas swelling (Section 8.3.4). Upon melting, all grain boundary gas is released immediately while the intra‑granular gas has a delayed coalescence. In fuel swelling, only the grain boundary gas is assumed to produce fuel swelling.
8.3.3.2. Isotropic Fission-gas Release¶
In the isotropic fission‑gas release model, the release is treated as a function of a single release rate fraction, \(f\), which is a function of temperature. This is the probability per unit time that a retained gas atom would be released. The basic rate equation governing the amount of retained gas in the fuel, at all locations, can be given by
(8.3‑31)
where
\(S\) = Amount of fission-gas retained in the fuel, kg
\(f\) = Fractional release rate of the retained gas, kg (kg-s) -1
\(G\) = Fission-gas production rate, kg s-1
Assuming that \(f\) and \(G\) are constant within the time step, \(\Delta t\), Eq. 8.3-31 may be integrated over the time step to yield the amount of retained gas at the end of the interval.
(8.3‑32)
Since the mobility of the gas atoms is a thermally activated process, it is assumed that the fractional release rate can be represented by
(8.3‑33)
where
\(A_{\alpha}\) = Pre-exponential input constant
\(Q_{\alpha}\) = Activation energy for release, input constant
The constants \(A_{\alpha}\) and \(Q_{\alpha}\) are determined through comparisons with experimentally determined values of the retained fission‑gas from the destructive examination of irradiated fuel pellets and through comparisons with more sophisticated fission‑gas release codes. Preliminary constants have been determined, but the validation exercises will be used to refine them.
8.3.3.3. Fission-gas Trap-release Model¶
A slightly more complex model that includes a more mechanistic treatment of fission‑gas release was developed by Weisman et al. [8‑15]. In this model the gas is assumed to be released in two ways: (1) direct release to the fuel surface, and (2) entrapment in the fuel matrix and subsequent release to the surface.
The amount of gas generated that is released directly is given by the following:
(8.3‑34)
where
\(\text{dn}_{1}\) = Amount of gas released in time increment \(\text{dt}\), kg
\(k'\) = Fraction of the free gas that escapes to the surface without becoming trapped
\(G\) = Fission-gas production rate, kg s-1
\(dt\) = Time increment, s
The amount of gas trapped in the fuel matrix is given by the total amount generated minus the total released.
(8.3‑35)
where
\(c\) = Amount of gas trapped in the fuel matrix, kg
\(t\) = Time, s
\(n\) = Amount of gas released, kg
If \(k\) is the probability that trapped gas will be released per unit time, then the amount of trapped gas that is released is given by
(8.3‑36)
where
\(\text{dn}_{\text{f}}\) = Amount of trapped gas which is freed, kg
Of this gas, only a fraction \(k'\) is released to the surface without becoming retrapped
(8.3‑37)
where
\(\text{dn}_{2}\) = Amount of trapped gas that is released to the fuel surface
The total amount of released gas, \(\text{dn}\), is therefore given by
(8.3‑38)
or upon substitution of Eqs. 8.3-34, 8.3-35, and 8.3-37 into Eq. 8.3-38,
(8.3‑39)
Integration of Eq. 8.3-39 is performed to give
(8.3‑40)
where
\(K = k'k\) = Probability that trapped gas is released from the fuel matrix to the fuel surface
Assuming that the reactor power history is described by a series of constant power steps, the amount of gas released during a constant power time step is given by
(8.3‑41)
where
\(\Delta n_{\text{i}}\) = Amount of gas released during time step \(\Delta t_{\text{i}}\), kg
\(G_{\text{i}}\) = Fission-gas generation rate during time step \(\Delta t_{\text{i}}\), kg s-1
\(\Delta t_{\text{i}}\) = Time-step duration, s
\(c_{\text{i}-1}\) = Amount of trapped gas at beginning of time step, kg
\(k'_{\text{i}},K_{\text{i}}\) = Defined above, but evaluated for the time step \(\Delta t_{\text{i}}\)
Equations for the terms \(k'\) and \(K\) were developed during the calibration of the FRAP‑S2 computer code [8‑16].
(8.3‑42)
(8.3‑43)
where
\(T\) = Temperature, K
\(d\) = Percent theoretical density of the fuel
\(Q_{\text{A}1}\), \(Q_{\text{A}2}\), \(Q_{\text{A}3}\), \(Q_{\text{A}4}\), \(Q_{\text{A}5}\) = Input constants
8.3.4. Fuel Swelling¶
In DEFORM‑4, the as‑fabricated porosity and the fission‑gas‑generated porosity are treated separately. The migration of the as‑fabricated porosity can lead to either densification or swelling of the fuel depending on local conditions (see Section 8.3.1). The newly formed porosity arising from fission‑gas bubbles introduces additional porosity that may be in a nonequilibrium condition, depending on the amount of gas in the bubbles, the local hydrostatic pressure, and the fuel surface tension. This fission‑gas porosity may increase or decrease as a function of time, producing changes in the fuel dimensions through swelling or densification. These changes in fuel porosity also affect the fuel thermal conductivity, since both the as‑fabricated and fission‑gas porosity are considered in the porosity terms. In addition to this gas effect, the solid fission products locate themselves interstitially in the fuel matrix, causing strains that produce swelling. Both these effects are accounted for by DEFORM‑4.
Swelling strains may occur both axially and radially. In general, the axial swelling strains in oxide fuels are relatively small compared to the thermal expansion effects. However, in some transients the differences caused by including the axial swelling can be enough to modify the accident scenario. For this reason, and to provide the basis for future versatility, axial swelling has been incorporated into DEFORM‑4. Radial swelling is important because of the effects on fuel‑cladding gap size and mechanical interaction. Both effects can produce large differences in the prediction of cladding failure, so radial swelling is also included in DEFORM‑4. These fuel swelling considerations are treated in the subroutine FSWELL.
8.3.4.1. Nonequilibrium Fission-gas Bubbles¶
The swelling rate due to fission gas depends on the release of the gas to grain boundaries and formation of fission‑gas bubbles. Detailed treatments for this process can be found in codes such as FRAS [8‑14] and GRASS‑SST [8-13]. The current model in DEFORM‑4 is much simpler and phenomenological on a more macroscopic level. While fission gas exists in both the fuel matrix and on grain boundaries, it is the bubbles on the grain boundaries that produce the significant swelling in oxide fuels. If these bubbles are underpressurized, a reduction in the bubble volume due to the fuel hydrostatic pressure will reduce the volume of a fuel cell. If the bubbles are overpressurized, an increase in bubble size, and thereby fuel cell volume can result. To determine the rate of swelling, or densification, the mechanical stresses (Section 8.2), internal gas pressure, pressure due to surface tension, and the creep properties of the fuel (Section 8.7.6) must be known.
While fission gas exists in both the fuel matrix and on the grain boundaries, it is the bubbles on the grain boundaries that produce significant swelling in oxide fuels. However, the actual amount of gas involved and its distribution changes with burnup. As discussed in Section 8.3.3.1, DEFORM-4 uses a fixed factor to distribute the generated fission gas between the fuel matrix and grain boundaries. However, this type of approach does not fully represent the gas mass associated with fuel swelling. Therefore, DEFORM-4 uses a burnup dependent parameter. FGMIN, to specify the amount of fuel matrix retained gas to associate with the fission gas induced swelling. Figure 8.3.1 shows the recommended curve for this fission gas parameter.
The treatment of the bubble gas pressure and surface tension follows that found in the LIFE code [8‑7]. This approach is macroscopic in nature and the constants used are based on the calibration of LIFE. The swelling rate of these bubbles is estimated from the fuel creep function. Swelling causes changes in the stress state of the fuel because the changes in geometry produce changes in the boundary conditions. But changes in stress states also produce changes in the swelling through changes in hydrostatic pressures. The swelling and mechanical responses are closely coupled. For this reason, the swelling calculation in DEFORM‑4 has been incorporated within the iterations to find the set of conditions that bring about consistency between the fuel and cladding. Swelling and mechanical strains are stored separately, but calculated considering mutual influences. The strains due to swelling/hot pressing of the fuel are added to the total mechanical deformation at the end of each time step.
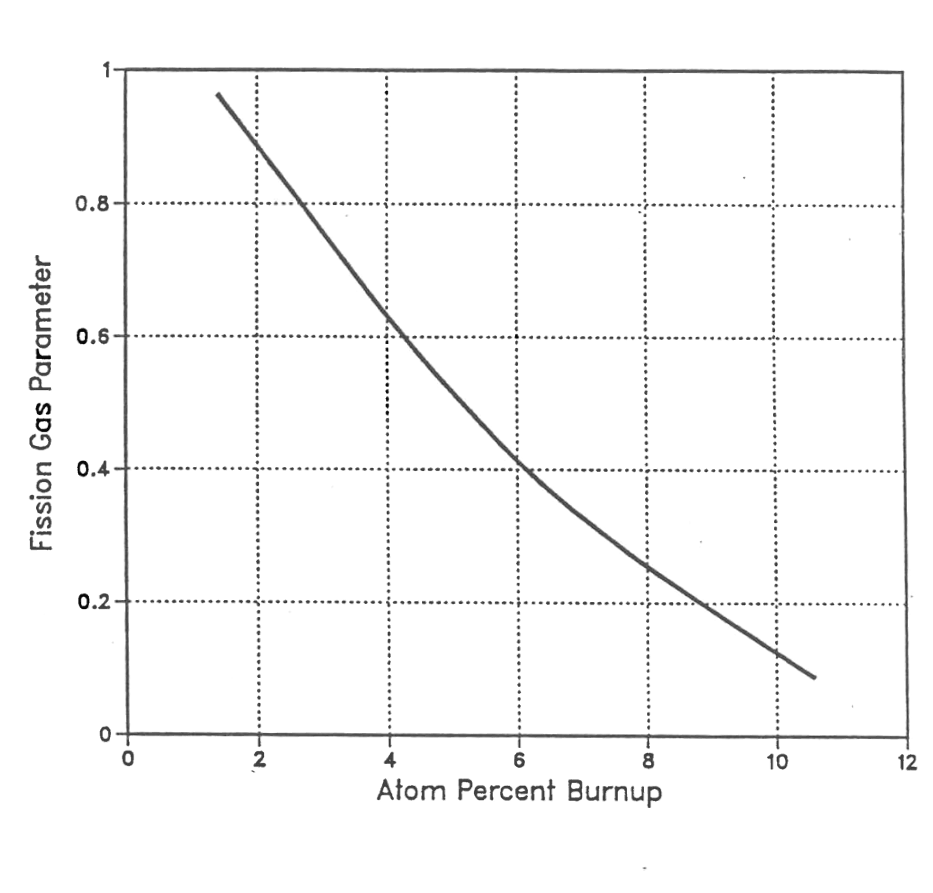
Figure 8.3.1 DEFORM-4 Fission Gas Parameter FGMIN¶
The pressure in the bubble necessary to balance the surface tension is parameterized as
(8.3‑44)
where
\(P_{\gamma}\) = Pressure due to surface tension effects, Pa
\(A_{\text{pg}}\) = Pre-exponential calibration constant, Pa
\(Q_{\text{pg}}\) = Exponential calibration constant, J(g-mole)-1
\(T\) = Temperature, K
\(R\) = Ideal-gas constant, J k-1(g-mole)-1
If the bubbles are assumed to be spherical, the relationship between surface tension pressure and bubble radius can be determined.
(8.3‑45)
where
\(r_{\text{B}}\) = Average fission-gas bubble radius, m
\(\gamma\) = Surface tension, N/m
The internal fission‑gas bubble pressure, \(P_{\text{fg}}\), is determined by the ideal‑gas law.
(8.3‑46)
where
\(P_{\text{fg}}\) = Pressure inside the fission gas-bubble, Pa
\(M_{\text{fg}}\) = Moles of fission gas in the bubbles
\(R\) = Ideal-gas constant
\(T\) = Temperature, K
\(V_{\text{fg}}\) = Volume of fission-gas bubbles in the cell, m3
The hydrostatic pressure of the fuel, \(P_{\sigma}\), is determined from the stress state in the fuel cell. The input parameter IPSIG determines the assumption used to define this pressure according to the following table.
IPSIG |
Definition of \(P_{\sigma}\) |
|---|---|
1 |
\(- \sigma_{\text{r}}\) |
2 |
\(- 1/2 (\sigma_{\text{r}} + \sigma_{\theta})\) |
3 |
\(- 1/3 (\sigma_{\text{r}} + \sigma_{\theta} + \sigma_{\text{z}})\) |
The imbalance between the bubble pressure and the external pressures is used to determine the effective creep rate of the fuel for swelling effects.
(8.3‑47)
where
\(\Delta P\) = Pressure differential
\(P_{\text{fg}}\) = Pressure in the bubbles
\(P_{\gamma}\) = Surface tension pressure
\(P_{\sigma}\) = Hydrostatic pressure
If the differential is positive, the bubbles will expand, swelling the fuel cell. If it is negative, the bubbles will contract, densifying the fuel cell. The process assumed to control the rate of these volume changes is the creep properties of the fuel in the cell.
There is a bubble volume that would cause Eq. 8.3-47 to become zero. The equilibrium volume, \(V_{\text{e}}\), is found by assuming the pressure differential is zero. To achieve this, the bubble pressure must balance the surface tension and hydrostatic pressures.
(8.3‑48)
Equation 8.3-46 is substituted into Eq. 8.3-48 and the result rearranged to determine the fission‑gas bubble equilibrium volume, \(V_{\text{o}}\)
(8.3‑49)
If all volume changes took place instantaneously, this would be the fission-gas bubble volume. However, it is assumed that the fuel creep properties define the rate of change of the volume and the driving force is the pressure differential. The following equation is therefore assumed to define the bubble volume rate of change.
(8.3‑50)
where
\(V_{\text{g}}\) = Fission-gas bubble volume, m3
\(V_{\text{e}}\) = Equilibrium fission-gas bubble volume, m3
\(\tau_{\text{c}}\) = Fuel creep time constant, s
\(t\) = Time, s
The fuel creep time constant, \(\tau_{\text{c}}\), is defined as the inverse of the fuel creep rate in the fuel cell under consideration with the pressure differential as the driving force. Integrating Eq. 8.3-50 over the time step, \(\Delta t\), and rearranging to find the fission-gas bubble volume at the end of the time step results in the following.
(8.3‑51)
The change in volume over the time step, \(\Delta V_{\text{s}} \left( \Delta t \right)\), is found by subtracting the volume at the beginning of the time step, \(V_{\text{g}} \left( t \right)\) from both sides of Eq. 8.3-51.
(8.3‑52)
Equation 8.3-52 gives the total volume change for a particular radial cell during the time step. When this change in volume takes place, part of it is radial volume expansion, typically 2/3, and the rest takes place axially. The radial component is handled nominally through the redefinition of the cell boundaries. The axial component requires special consideration because of the assumption of generalized plane strain. Each radial cell will produce a different axial strain due to the swelling process. A plane strain is determined that moves the same mass of fuel across the original axial segment boundary.
(8.3‑53)
where
\(\Delta V_{\text{s,i}}\) = Volume change due to swelling for radial node \(i\), m3.
\(f_{\text{a}}\) = Fraction of total swelling taking place axially.
This change would result in a new axial segment length.
(8.3‑54)
where
\(\Delta h_{\text{s,i}}\) = Axial segment length change from swelling, m
\(r_{\text{i}+1}\) = Outer radius of radial cell i after swelling is included, m
\(r_{\text{i}}\) = Inner radius of radial cell i after swelling is included, m.
Combining Eqs. 8.3-53 and 8.3-54, the segment length change for radial cell \(i\) can be found
(8.3‑55)
The axial strain for the cell can then be found
(8.3‑56)
where
\(h\) = Axial segment length at beginning of time step, m
The fraction of the fuel mass that has moved from the original segment length, \(h\), into the additional length, \(\Delta h_{\text{s,i}}\), is the ratio of the length change to the new length, assuming uniform mass distribution within the segment
(8.3‑57)
where
\(F_{\text{i}}\) = Fraction of original cell mass moved into length \(\Delta h_{\text{s,i}}\).
Using Eqs. 8.3-56 and 8.3-57, this mass fraction can be defined in terms of the axial strain
(8.3‑58)
The total mass movement across the original boundary can therefore be determined
(8.3‑59)
where
\(M_{\text{aT}}\) = Total fuel mass moved out of original segment length, kg
\(M_{\text{i}}\) = Fuel mass in radial cell \(i\)
\(N_{\text{t}}\) = Total number of radial cells
A generalized axial swelling strain using Eqs. 8.3-58 and 8.3-59 can now be defined that gives this same mass transfer.
(8.3‑60)
where
\(z_{\text{s,a}}\) = Generalized axial swelling strain
\(M_{\text{T}}\) = Total mass in the axial segment
Solving Eq. 8.3-60 yields the desired result of an axial strain that is uniform over the radial cross section, but produces the same mass movement as the sum of the individual radial cell components
(8.3‑61)
These fission gas bubble swelling considerations are handled by the subroutine FSWELL.
8.3.4.2. Solid Fission-product Swelling¶
In addition to the gaseous fission‑product swelling, there is solid fission‑product swelling from products such as zirconium, niobium, molybdenum, the rare earths, yttrium, etc. A detailed treatment of these solid fission products, which considered their physical and chemical state to determine the partial volumes, would yield the lattice strain created. This, together with the isotopic yields from fission, would result in a mechanistic estimate of solid product swelling. This type of treatment requires more computational resources than are warranted for the magnitude of the phenomenon.
A simpler model is assumed which relates the fractional volume change to the fuel burnup.
(8.3‑62)
where
\(\left( \frac{\Delta V}{V} \right)_{\text{SP}}\) = Fractional volume change due to solid fission products
\({\dot{\varepsilon}}_{\text{sfp}}\) = Solid fission-product swelling rate parameter, \(\left( \Delta V/ V \right)\) (atom % burnup)-1
B = Fuel burnup, atom %
Due to uncertainties in the thermodynamic state and migration characteristics of the products, the value of \({\dot{\varepsilon}}_{\text{sfp}}\) is specified by an input parameter.
The volume changes from solid product changes are included with those of the volatile products when determining the changes in fuel volume that may change the fuel‑cladding interface conditions. However, this volume change is not affected by the local hydrostatic pressure and therefore remains a constant through the iterations mentioned in the previous section and discussed at length in Section 8.5.
8.3.5. Irradiation-induced Cladding Swelling¶
When 20% cold‑worked 316 stainless steel material is irradiated in a fast neutron flux, there is a temperature‑ and flux‑dependent reduction in density through the formation of irradiation‑induced voids. The model in DEFORM‑4 is based on an empirical correlation corresponding to stress‑free swelling in the Nuclear Systems Material Handbook [8‑17]. The volume change is represented by
(8.3‑63)
where
\(\sum\) = Negative fractional density change
(8.3‑64)
\(\rho_{\text{f}}\) = Final immersion density
\(\rho_{\text{o}}\) = Initial immersion density
To find the change during the time step, the derivative of Eq. 8.3-63 is
(8.3‑65)
The correlation represents two characteristics of irradiation‑induced swelling based on experimental findings. First, the rate of swelling for 20% cold‑worked 316 stainless steel is temperature sensitive. Second, there appears to be an incubation period during which little change in density is observed. The form given in the NSMH for the negative fractional density change is
(8.3‑66)
where
\(R \left( T \right)\) = Temperature-dependent rate parameter
\(\phi\) = Fast neutron flux
\(t\) = Time
\(\alpha\) = Calibration constant
\(\tau\) = Incubation parameter
The derivative of Eq. 8.3-66 gives
(8.3‑67)
The fractional volume change is, therefore, determined from
(8.3‑68)
The swelling is assumed to be isotropic and always outward. The new cross sectional area, \(A\), is calculated assuming 1/3 of the volume change takes place axially.
(8.3‑69)
where
\(A\) = Cross-sectional area
\(r_{\text{o}} \left( t \right)\), \(r_{\text{o}} \left( t + \Delta t \right)\) = Outer radius at the beginning and end of the time step
\(r_{\text{i}} \left( t \right)\), \(r_{\text{i}} \left( t + \Delta t \right)\) = Inner radius of the beginning and end of the time step
The new inner radius is calculated from
(8.3‑70)
The forms given for the rate and incubation parameter are given below.
(8.3‑71)
(8.3‑72)
(8.3‑73)
where
\(\beta\) = (T - 500)/1000
\(T\) = Temperature, °C
The rate, \(R\), and incubation, \(\tau\), parameters needed in Eq. 8.3-67 have several options which are controlled through the input parameters IRATE and ITAU. The confidence limits on the use of these equations suggest the use of upper and lower bounds on \(R\) and \(\tau\). Nominal values are obtained with no multipliers to these parameters. The input parameters IRATE and ITAU can be used to select the specified bound as illustrated below. Input values of zero give the nominal parameters. If cladding swelling does not occur, the values of ITAU and IRATE can be set to bypass the swelling calculation.
Limits on steady‑state swelling rate parameter, \(R\):
Upper bound (IRATE = 1)
(8.3‑74)
where
\(T\) = Temperature, °C
(8.3‑75)
Lower bound (IRATE = ‑1)
(8.3‑76)
No swelling (IRATE = ‑2)
Limits on incubation parameter \(\tau\):
Upper bound (ITAU = 1)
(8.3‑77)
Lower bound (ITAU = ‑1)
(8.3‑78)
No swelling (ITAU = ‑2)
These equations are solved in the subroutine CLADSW.
8.3.6. Fission-gas Plenum Pressure¶
As the volatile fission products are released from the fuel, they enter the free volume associated with the fuel pin and are assumed to mix homogeneously with the gases already present. The free volumes considered are the fabricated fission gas plenum, the central fuel void not associated with a central molten fuel cavity, the fuel‑cladding gap, and the crack volume within the fuel. A homogeneous ideal‑gas mixture that is in pressure equilibrium is assumed to form.
The total number of moles of fission gas and helium is known prior to the pressure calculation, although the distribution is not known.
(8.3‑79)
where
\(n_{\text{T}}\) = Total moles of gas
\(n_{\text{T}}^{\text{fp}}\) = Moles of fission product gas
\(n_{\text{T}}^{\text{He}}\) = Moles of helium
The amount of helium is known from the fill gas pressure, the fraction that is not helium, and the reference temperature geometry. The amount of helium also contains the amount released as porosity migration occurs (Section 8.3.1). The number of moles of fission gas is known from the fission gas release calculation (Section 8.3.3) and the non‑helium initial fill gas.
If all the free volume exists at the same pressure, \(P_{\text{g}}\), then the number of moles of gas at any specific free volume location can be determined from the ideal gas law.
(8.3‑80)
where
\(n_{\text{i}}\) = Moles of gas in free volume \(i\)
\(P_{\text{g}}\) = Pressure of the gas, Pa
\(R\) = Ideal-gas constant, J K-1 (g-mole)-1
\(V_{\text{i}}\) = Volume of free volume \(i\), m3
\(T_{\text{i}}\) = Temperature of free volume \(i\), K
This basic relationship can be used to determine the moles of gas associated with the types of free volumes listed above. For the plenum, there exists only one volume and temperature.
(8.3‑81)
where
\(n_{\text{p}}\) = Total number of moles in the plenum
\(V_{\text{p}}\) = Volume of the fission gas plenum, m3
\(T_{\text{p}}\) = Temperature of the fission gas plenum, K
The central fuel void may exist over a number of axial segments due to as‑fabricated porosity or the fuel initially fabricated with a central hole. Therefore, each axial segment contributes to the number of moles.
(8.3‑82)
where
\(n_{\text{v}}\) = Total number of moles in central void
\(V_{\text{v,j}}\) = Volume of central void in axial segment \(j\), m3
\(T_{\text{v,j}}\) = Temperature of the central void in axial segment \(j\), K
\(MZ\) = Number of axial nodes
If an axial segment has a central void included as part of the molten cavity, its contribution is not included in Eq. 8.3-82.
The fuel‑cladding gap can also contain the released gases. It also exists over a number of axial nodes, and its contribution to the total moles of gas is a summation over all axial segments.
(8.3‑83)
where
\(n_{\text{g}}\) = Total number of moles in fuel-cladding gap
\(V_{\text{g,j}}\) = Volume of fuel-cladding gap in axial segment \(j\), m3
\(T_{\text{g,j}}\) = Temperature of the fuel-cladding gap, \(K = 0.5 \left( T_{\text{f,j}} + T_{\text{c,j}} \right)\)
\(T_{\text{f,j}}\) = Fuel surface temperature in axial segment \(j\), K
\(T_{\text{c,j}}\) = Inner cladding surface temperature in axial segment \(j\), K
The volume associated with the crack volume requires a summation over both the radial extent of cracking and the axial segments. In a given axial segment, the volumes and temperatures change with the radius.
(8.3‑84)
where
\(n_{\text{k}}\) = Total number of moles in the crack volume
\(V_{\text{k,i,j}}\) = Volume of cracks in radial cell \(i\) of axial segment \(j\), m3
\(T_{\text{k,i,j}}\) = Temperature of fuel in radial cell \(i\) of axial segment \(j\), K
IETA = Innermost cracked fuel node
NT = Total number of radial fuel nodes
It is assumed that the gas in the cracks of the fuel is in thermal equilibrium with the fuel in the same cell.
Since the total number of moles must reside in the free volumes considered, Eq. 8.3-79 can be combined with Eqs. 8.3-81 through 8.3-84
(8.3‑85)
Everything in Eq. 8.3-85 is known except the gas pressure, therefore the equation can be solved to find the pressure.
(8.3‑86)
Once the uniform pressure has been determined from Eq. 8.3-86, and using the known ratio of fission product moles to helium moles with Eq. 8.3-79, the number of moles of fission gas and helium can be found in any of the free volumes.
These calculations are performed in the subroutine PRESPL.
8.3.7. Molten Cavity Pressurization¶
Prior to fuel melting, the central void and plenum are assumed to be in pressure equilibrium. Once melting has begun, DEFORM‑4 provides for three different methods for calculating the molten cavity pressure: (1) the cavity under consideration extends axially only over the range of segments where melting has occurred, (2) the cavity extends over all axial segments, and (3) each axial segment is considered a separate cavity. These options are controlled by the input variable IMELTV.
IMELTV |
Description |
|---|---|
0 |
Molten cavity extends only over the axial extent of fuel melting |
1 |
Molten cavity extends over all axial segments |
2 |
Each axial segment treated as a separate control volume |
If a central void exists before fuel melting, then the first two options give similar results. The second option presents a more mechanistic approach to the molten cavity. As melting begins, it is expected that communication would exist all along the central void. As the available volume for the helium and fission gas associated with one axial segment is decreased because of fuel melting and thermal expansion, the excess gas would move to other segments to produce a balanced pressure all along the central void. This model assumes that the transient time scales are long enough to allow this redistribution process.
The third option is included for the study of extremely fast transients. If the time scale is short enough to preclude material redistribution, then each axial segment is assumed to act as a separate molten cavity. A separate pressure is calculated for each segment, and axial pressure differentials are produced. The effects of these axial differentials on the radial mechanics solution in the cladding can then be studied to determine the sensitivity of cladding failure location.
In addition to these options, the effects of fuel moving into the cracks and pressurizing them to the same level as the molten cavity can be studied through the input parameter IROR. If this parameter is set to 1, the crack volume is included in the molten cavity volume and the cavity pressure acts directly on the cladding, see Section 8.2.3. Because DEFORM‑4 does not consider mass transport between axial segments or radial cells, the actual movement of fuel cannot take place. The consideration of the crack volume does allow the macroscopic effect of volume increase in the molten cavity by movement of molten fuel out of the cavity into crack volume to be considered.
When the PINACLE module is initiated, which describes the pre-failure in-pin molten fuel relocation, it provides the molten cavity pressure that is a boundary condition for the DEFORM calculation. This module replaces the CAVITY subroutine in DEFORM. DEFORM and PINACLE work interactively with PINACLE providing the temperatures and molten cavity pressures for DEFORM, and DEFORM determining the fuel pin thermal/mechanical response to changes in these conditions and returning to PINACLE the new axial and radial node locations.
The following calculations are performed in the subroutine CAVITE.
8.3.7.1. Incremental Melt Fraction Ratio¶
The radial extent of the molten cavity is determined by the relationship between the radial cell temperature and the solidus temperature. Melting of the cell is assumed to begin when the solidus temperature is reached, and be complete when the liquidus temperature is attained.
(8.3‑87)
where
\(f_{\text{m,i}}\) = Melt fraction of radial cell \(i\)
\(t\) = Time at beginning of the time step, s
\(\Delta t\) = Time step length, s
\(T_{\text{2,i}}\) = Temperature of radial cell i at end of time step, K
\(T_{\text{S}}\) = Solidus temperature, K
\(T_{\text{l}}\) = Liquidus temperature, K
As the cell melts, the amount of material considered to be in the molten region of the cell is directly related to the melt fraction, \(f_{\text{m,i}}\). However, the original fission gas content, etc., is not saved from one time step to the next, but the values at the end of the time step are determined, so a simple relationship between melt fraction change and material distribution between the molten state vs the solid state based on the current melt fraction cannot be used. It is necessary to develop an approach based on the solid fuel quantities at the beginning of the time step and the melt fraction change during the time step. This relationship is known as the incremental melt fraction ratio. With this approach, the cell can be considered to melt into the molten cavity in an incremental fashion rather than adding the node to the cavity all at one time when some arbitrary melt fraction has been reached.
Prior to melting, a radial cell contains some predetermined amount of a specific constituent that is important to the cavity pressurization, such as fission gas, as‑fabricated gas and volume, crack gas and volume, etc. At the first step where melting occurs, some part of this is transferred from the solid region into the molten region.
(8.3‑88)
(8.3‑89)
where
\(F_{\text{m,i}} \left( 1 \right)\) = Amount of constituent in the molten region at end of time step 1 in radial cell \(i\)
\(F_{\text{o,i}}\) = Total amount of constituent in solid fuel prior to melting
\(F_{\text{s,i}} \left( 1 \right)\) = Amount of constituent remaining in solid region at end of time step 1 in radial cell \(i\)
At end of the second time step with melting, the amounts in the molten and solid regions are related to the new time step melt fraction
(8.3‑90)
(8.3‑91)
Equations 8.3-90 and 8.3-91 can be rewritten in terms of the known quantities \(F_{\text{m,i}} \left( 1 \right)\) and \(F_{\text{s,i}} \left( 1 \right)\) rather than the now unknown, \(F_{\text{o,i}}\) by rearrangement of Eqs. 8.3-88 and 8.3-89.
(8.3‑92)
(8.3‑93)
As the process continues, the relationship between the constituents and melt fractions at a specific time can be generalized.
(8.3‑94)
(8.3‑95)
The change in the constituent during the time step can be determined by subtracting the results of two time steps and making use of the generalized form of Eq. 8.3-89.
(8.3‑96)
\(\Delta F_{\text{s,i}}\) = Change in constituent in solid fuel in radial cell \(i\) that takes place during the time step
The same procedure applied to the change in the molten region constituent results in the negative of Eq. 8.3-96, as would be expected for conservation.
The considerations leading to Eq. 8.3-96 define what is known as the incremental melt fraction ratio.
(8.3‑97)
where
\(R_{\text{IMF}}\) = Incremental melt fraction ratio
This ratio is used in the considerations given below.
8.3.7.2. Gas Release on Melting¶
When melting begins in an axial segment, there are five constituents from which gas and volume may be moved into the molten cavity: (1) the initial central void, (2) the grain boundaries, (3) intragranular, (4) the as-fabricated porosity, and (5) the fuel cracks. Each of these can affect the molten cavity pressurization through the gas and volume associated with their inclusion and will be described below. In the discussion in the next five sections, each constituent is treated as a single adjustment to the cavity gas and volume consideration, while in actuality they are accumulated for the total change to the cavity.
8.3.7.2.1. Central Void Considerations¶
Prior to melting, the central void is considered to be in equilibrium with the rest of the free volume within the pin. The number of moles of helium and fission gas associated with the central void in each axial segment varies depending on the volume, temperature, and pressure, and was discussed in Section 8.3.6. The amount of this gas, therefore, changes during each time step throughout the pretransient and transient up to fuel melting initiation.
Upon initial melting, the gas associated with the defined central molten cavity, see definition of IMELTV above, is fixed at its last value based on equilibrium with the plenum and associated free volume within the pin. This gas and its volume is then considered part of the molten cavity and is removed from the plenum pressure considerations. It is implicitly assumed that melting initiates the production on a molten cavity region, which acts as a bottle that does not communicate with the plenum.
This central void consideration defines the initial state associated with the molten cavity.
8.3.7.2.2. Grain Boundary Gas¶
As described in Section 8.3.3 and Section 8.3.4 above, the fission gas is assumed to exist in grain boundary bubbles that cause fuel swelling, and intragranular gas within the fuel matrix. Upon fuel melting, the grain boundary gas and its volume is assumed to be released immediately into the molten cavity. Based on the discussion in Section 8.3.7.1, Eqs. 8.3-96 and 8.3-97 can be used to determine the gas released from the grain boundary to the molten cavity.
(8.3‑98)
(8.3‑99)
where
\(\Delta M_{\text{gb,i,j}} \left( \Delta t \right)\) = Change in moles of fission gas on the grain boundary during the time step in radial cell \(i\) of axial segment \(j\)
\(M_{\text{gb,i,j}} \left( t \right)\) = Moles of fission gas on the grain boundary at beginning of the time step for radial cell \(i\) of axial segment \(j\)
\(\Delta M_{\text{c,gb}} \left( \Delta t \right)\) = Moles of fission gas added to the molten cavity from the grain boundaries during the time step
\(R_{\text{IMF,i,j}}\) = Incremental melt fraction ratio for radial cell \(i\) of axial node \(j\)
The volumes associated with the grain boundary gas is assumed to be moved to the molten cavity in the same proportion as the moles.
(8.3‑100)
(8.3‑101)
where
\(\Delta V_{\text{gb,i,j}} \left(\Delta t \right)\) = Change in volume of the fission gas on the grain boundaries during the time step in radial cell \(i\) of axial segment \(j\), m3
\(V_{\text{gb,i,j}} \left( t \right)\) = Volume of gas on grain boundaries at beginning of the time step for radial cell \(i\) of axial segment \(j\), m3
\(\Delta V_{\text{c,gb}} \left( \Delta t \right)\) = Volume added to molten cavity from grain boundaries during the time step, m3
As a cell progresses from initial melting to fully molten, all the grain boundary gas and volume is moved into the molten cavity.
Equations 8.3-98 through 8.3-101 all refer to a single radial node. The total amount of gas and volume moved into association with the molten cavity is found through a summation of these equations over all melting radial cells at all axial segments in the cavity. Combining Eqs. 8.3-98 and 8.3-99, and Eq. 8.3-100 and 8.3-101,
(8.3‑102)
(8.3‑103)
where
\(\Delta M_{\text{c,gb}}^{T}\) = Total moles of gas added to molten cavity from the grain boundaries during the time step
\(\Delta V_{\text{c,gb}}^{T}\) = Total volume of grain boundary gas added to molten cavity during the time step, m3
\(j_{\text{cavb}}\) = Axial segment number at bottom of molten cavity
\(j_{\text{cavt}}\) = Axial segment number at top of molten cavity
\(iz\) = Radial boundary number that defines the boundary between the molten and solid region
8.3.7.2.3. Intra-Granular Gas¶
While the grain boundary gas is assumed to move instantaneously into the molten cavity, the intragranular gas is assumed to be tied‑up in very small bubbles or interstitially located, so a time is required for the coalescence and buoyancy forces to release this gas into the cavity. Therefore, there can be gas in the molten fuel region which has not been released into the molten cavity.
The intra‑granular gas is transferred from the solid fuel into the molten fuel based on the considerations presented in Section 8.3.7.1.
(8.3‑104)
(8.3‑105)
(8.3‑106)
where
\(\Delta M_{\text{m,ig}} \left(\Delta t \right)\) = Moles of intra-granular fission gas transferred from the solid to the molten fuel during the time step for the radial cell
\(M_{\text{ig,i,j}} \left( t \right)\) = Moles of intra-granular fission gas at beginning of the time step in radial cell \(i\) of axial segment \(j\)
\(M_{\text{ig,i,j}} \left( t + \Delta t \right)\) = Moles of intra-granular fission gas at end of time step
\(M_{\text{m,ig}} \left( t + \Delta t \right)\) = Moles of gas retained in molten fuel at end of time step
The intra‑granular gas is assumed to have no volume associated with it, so no volume movement occurs.
The release of the gas retained within the molten fuel to the molten cavity through coalescence and buoyancy effects is assumed to occur at a rate proportional to the amount of gas present.
(8.3‑107)
where
\(\tau_{\text{g}}\) = Time constant for coalescence release, s-1
Equation 8.3-107 is integrated over the time step to determine the release from the molten fuel to the molten cavity.
(8.3‑108)
(8.3‑109)
where
\(\Delta M_{\text{c,ig}} \left( \Delta t \right)\) = Moles of intra-granular gas added to molten cavity during the time step
\({M'}_{\text{m,ig}} \left( t + \Delta t \right)\) = Moles of intra-granular gas remaining in the molten fuel at the end of the time step after both transfer from solid fuel and release to the cavity
Because this varies with each radial cell and axial segment, the total change is found through the double summation as with Eq. 8.3-102 above.
(8.3‑110)
where
\(\Delta M_{\text{c,ig}}^{T}\) = Total moles of gas added to molten cavity from the intragranular gas during the time step
8.3.7.2.4. As-Fabricated Gas¶
Like the grain boundary gas, the gas and volume associated with any residual as‑fabricated porosity, see Section 8.3.1, is assumed to be released to the molten cavity instantaneously upon melting.
(8.3‑111)
(8.3‑112)
(8.3‑113)
(8.3‑114)
where
\(\Delta M_{\text{c,af}}\) = Moles of as-fabricated, retained helium added to the molten cavity
\(M_{\text{af,i,j}}\) = Moles of as-fabricated, retained helium that remains in the solid fuel of radial cell \(i\) of axial segment \(j\)
\(\Delta V_{\text{c,af}}\) = Volume of as-fabricated, retained porosity added to the molten cavity, m3
\(V_{\text{af,i,j}}\) = Volume of as-fabricated, retained porosity that remains in the solid fuel of radial cell \(i\) of axial segment \(j\)
The contributions must be summed over all radial cells of all axial segments considered to be a part of the molten cavity.
(8.3‑115)
(8.3‑116)
where
\(\Delta M_{\text{c,af}}^{T}\) = Total moles of gas added to molten cavity from the as-fabricated porosity during the time step
\(\Delta V_{\text{c,af}}^{T}\) = Total volume added to the molten cavity from the as-fabricated porosity during the time step
8.3.7.2.5. Fuel Crack Gas¶
As the radial cell melts into the molten cavity, the gas and volume associated with cracks within the fuel are assumed to be added to the cavity instantaneously. The amount of gas within the cracks depends on the plenum pressure and the temperature of the cell, for all are assumed to be in equilibrium with the plenum.
(8.3‑117)
where
\(M_{\text{ck,i,j}}\) = Moles of gas (fission gas + helium) in the crack volume of radial cell \(i\) of axial segment \(j\)
\(P_{\text{g}}\) = Plenum pressure, Pa
\(V_{\text{ck,i,j}}\) = Volume of cracks of radial cell \(i\) of axial segment \(j\), m3
Ti,j = Temperature of radial cell \(i\) of axial segment \(j\), m3
The amount of gas and volume moving into the molten cavity is again determined from the incremental melt fraction ratio and the initial conditions.
(8.3‑118)
(8.3‑119)
(8.3‑120)
(8.3‑121)
where
\(\Delta M_{\text{c,ck}}\) = Moles of crack volume gas added to the molten cavity
\(\Delta V_{\text{c,ck}}\) = Volume of cracks added to the molten cavity, m3
The total contributions are then summed over all melting radial cells of all axial segments in the molten cavity.
(8.3‑122)
(8.3‑123)
where
\(\Delta M_{\text{c,ck}}^{T}\) = Total moles of crack volume gas added to the molten cavity during the time step
\(\Delta V_{\text{c,ck}}^{T}\) = Total volume added to the molten cavity during the time step form cracks, m3
As crack volume gas is added to the molten cavity, it is removed from the plenum pressure calculation along with its associated volume, thereby maintaining conservation of gas.
8.3.7.3. Fuel Volume Changes¶
The discussion above covered the movement of gas and volume from various sources into the molten cavity. There are two other effects which will change the volume associated with the molten cavity: (1) fuel volume change on melting, and (2) molten fuel thermal expansion. Any changes due to swelling or contraction of the remaining grain boundary fission gas bubbles are treated in the fuel swelling routine, see Section 8.3.4.
DEFORM‑4 contains the function routine RHOF, which determines the theoretical density of the fuel at any given temperature, see Section 8.7.1. Since it is assumed that there is no mass transfer between radial cells or axial segments, the volume change for each cell can be determined
(8.3‑124)
where
\(\Delta V_{\text{th,i,j}}\) = Volume change caused by temperature changes during the time step for radial cell \(i\) of axial segment \(j\), m3
\(\rho\) = Temperature dependent fuel theoretical density, kg/m3
\(T_{\text{2,i,j}}\) = Final temperature of radial cell \(i\) of axial segment \(j\), \(K\)
\(T_{\text{1,j,i}}\) = Initial temperature of radial cell \(i\) of axial segment \(j\), K
\(F_{\text{i,j}}\) = Mass of fuel in radial cell \(i\) of axial segment \(j\), kg
Because the density function already incorporates the changes due to melting over the melting range, there is no need to use the incremental melt fraction ratio.
Summing over all radial cells and axial segments results in the total volume change due to thermal affects in the fuel
(8.3‑125)
where
\(\Delta V_{\text{c,th}}^{T}\) = Total volume change in molten cavity due to changes in temperature in the fuel, m3
8.3.7.4. Molten Cavity Pressure¶
The molten cavity pressure is determined from the ideal gas law.
(8.3‑126)
where
\(P_{\text{cav}}\) = Molten cavity pressure, Pa
\(M_{\text{cav}}\) = Total moles of gas in molten cavity
\(T_{\text{cav}}\) = Molten cavity temperature, K
\(V_{\text{cav}}\) = Molten cavity volume, m3
The number of moles of gas in the cavity is determined by adding the changes discussed above to the amount present at the start of the time step. The volume is similarly determined.
(8.3‑127)
(8.3‑128)
where
\(M_{\text{c,i}}\) = Initial moles of gas present in the molten cavity
\(V_{\text{c,i}}\) = Initial volume present in the molten cavity.
It is assumed that the boundary between the outer most cell that is melting and the solid fuel remains stationary during the time step. While this is not necessarily true, appropriate choice of the transient time step length will provide a close link between cavity pressurization and mechanical response to this force without the need to iterate between the cavity pressure and mechanical response parts of the code.
Because of the volume changes occurring as a transient progresses, it is possible for the central void to completely close. The case may even exist where there is more volume needed than exists inside the solid boundary. Because DEFORM‑4 does not provide for relocation of fuel between axial segments, the additional material cannot be moved. However, to at least study the pressurization effects, when this situation arises, a volume deficit is calculated.
(8.3‑129)
where
\(V_{\text{d,j}}\) = Volume deficit for axial segment \(j\), m3
\(V_{\text{f,j}}\) = Volume the fuel would require at axial segment \(j\), m3
\(V_{\text{sb,j}}\) = Volume available inside the solid fuel boundary, m3
These values are summed over all axial segments to provide the total volume mismatch.
(8.3‑130)
This value is then used to decrease the apparent volume given by Eq. 8.3-128.
(8.3‑131)
The temperature used in Eq. 8.3-126 is an averaged value for the cavity. First the radially mass averaged temperature of the molten fuel for each axial segment is determined. These temperatures are then weighted based on the volume available at each axial segment for gas to occupy.
(8.3‑132)
(8.3‑133)
where
\(T_{\text{ma,j}}\) = Radially mass averaged fuel temperature over molten region, K
\(T_{2,\text{i,j}}\) = Temperature of radial cell \(i\) of axial segment \(j\), K
\(F_{\text{i,j}}\) = Mass of radial cell \(i\) of axial segment \(j\), kg
\(V_{\text{c,j}}\) = Volume of the central void at axial segment \(j\), m3
Using the values determined from Eqs. 8.3-133, 8.3-131, and 8.3-127, the molten cavity pressure is calculated from 8.3-126. This procedure is carried out at the beginning of each time step, so the dimensional changes from the previous time step are used to calculate the molten cavity pressure to be used as the boundary condition for the current time step.
8.3.7.5. Fuel Vapor Pressure¶
In addition to the pressure from the gases in the molten cavity, the fuel vapor pressure is included. The temperature used is the maximum radially mass‑averaged temperature over the axial extent of the cavity. In the case where each axial segment is a separate cavity, the mass‑averaged temperature of the segment is used. The fuel vapor pressure terms are added to the gas induced pressure to obtain the total molten cavity pressure.
8.3.8. Fuel-cladding Gap Conductance¶
The thermal coupling between the cladding and the fuel is important because it affects the fuel and coolant temperatures and thereby, the swelling and thermal expansion of the fuel and cladding. The gap conductance provides this coupling. If the values are high, the fuel temperatures are lower, reducing the fuel swelling, thermal expansion, restructuring, fission‑gas release, and stored energy. If the gap conductance is poor due to a large gap or a low conductivity gas mixture in the gap, then all fuel temperatures are raised, enhancing the phenomena mentioned previously. Because of the sensitivity of phenomena to temperature, and therefore gap conductance, it is best to describe the elements that contribute to the heat transfer between the fuel and cladding as mechanistically as possible.
SAS4A contains three options for calculating the gap conductances. In order of decreasing mechanistic consideration they are (1) a modified Ross-Stoute model [8‑18], (2) a SAS3D parametric model, and (3) a simple SAS3D inverse‑gap‑size model. These are discussed below. It is recommended that the modified Ross‑Stoute be used because of the more mechanistic nature of its formulation.
The gap conductance is determined at the end of each DEFORM‑4 time step, and is used for the fuel‑cladding thermal coupling when determining the temperatures at the end of the next time step. The modified Ross‑Stoute model is coded in the function HGAP. The other two models are coded in the function HBFND. It is not possible to switch between models during the calculation because of modeling inconsistancies and the large changes that might result.
8.3.8.1. Modified Ross-Stoute Gap Conductance Model¶
The recommended gap conductance model is a modified Ross‑Stoute model [8-18]. This model has been used extensively in such codes as LIFE‑III [8‑5] and GAPCON [8‑19] and is considered the most mechanistic model currently available. The heat transfer through the fuel‑cladding interface is considered to consist of three components: (1) conduction through the gas between the fuel and the cladding, (2) radiative transfer between the fuel and cladding surfaces, and (3) solid‑to‑solid heat transfer if the fuel and cladding are in contact. Even if contact does occur, the model still assumes the existence of a gas gap between the surfaces, a result of the effects of the surface roughnesses, which are input parameters. If there is no contact, then the solid‑to-solid component is set to zero. Figure 8.3.2 illustrates the fuel‑cladding geometry and considerations for the open and closed gap cases.
8.3.8.1.1. Radiative Heat Transfer¶
The radiative heat‑transfer coefficient, \(h_{\text{r}}\), is determined from
(8.3‑134)
where
\(h_{\text{r}}\) = Radiative heat-transfer coefficient, W m-2 K-1
\(q_{\text{r}}\) = Heat transferred from the hotter to the colder surface, W
\(A_{\text{f}}\) = Surface area of the fuel from which \(q_{\text{r}}\) is transferred, m2
\(T_{\text{f}}\) = Temperature of the fuel outer surface, the hotter one, K
\(T_{\text{c}}\) = Temperature of the cladding inner surface, the colder one, K
For radiative heat transfer between two surfaces,
(8.3‑135)
where
\(\sigma\) = Stefan-Boltzmann constant, W m-2 K-4
\(\varepsilon_{\text{f}}\) = Emissivity of the fuel surface
\(\varepsilon_{\text{c}}\) = Emissivity of the cladding surface
\(A_{\text{c}}\) = Inner surface area of the cladding to which the heat is being transferred, m2
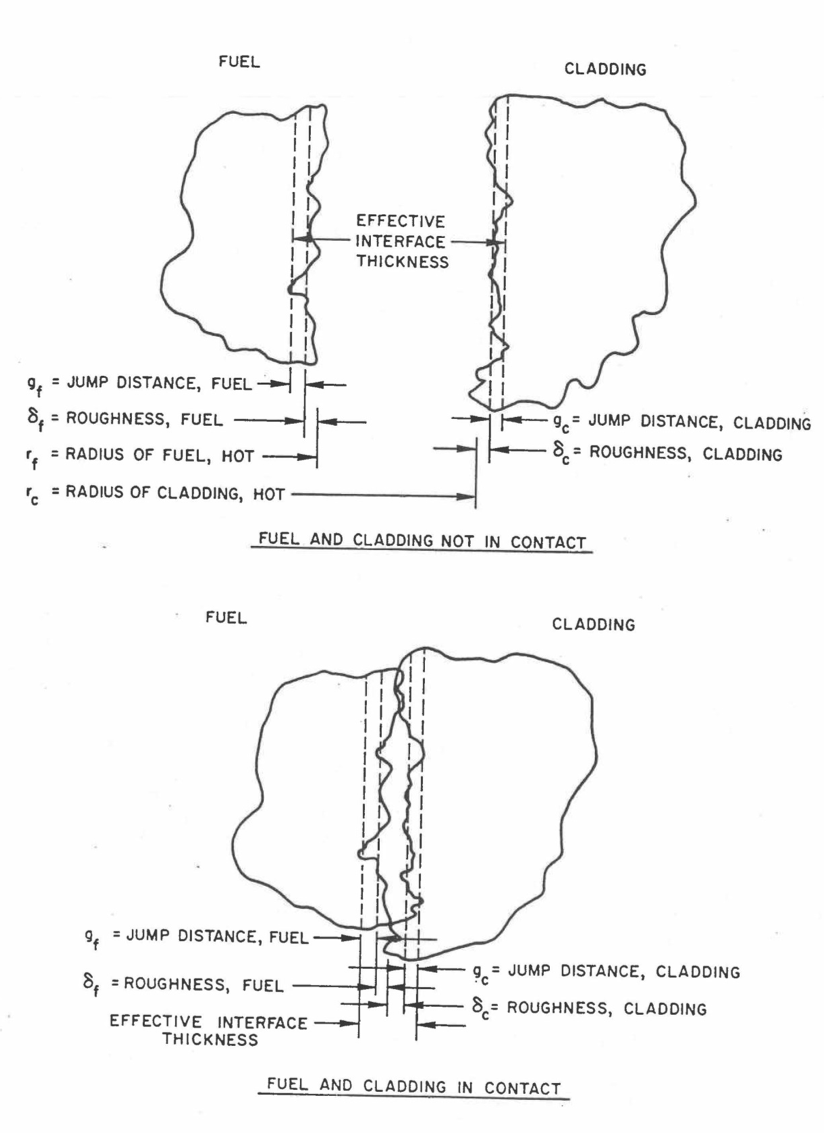
Figure 8.3.2 Geometry of the Fuel-cladding Gap¶
Combining Eqs. 8.3-134 and 8.3-135 provides the following result for the radiative heat‑transfer coefficient.
(8.3‑136)
where
\(r_{\text{f}}\) = Outer radius of the fuel, m
\(r_{\text{c}}\) = Inner radius of the cladding, m
8.3.8.1.2. Conduction Heat Transfer¶
The heat‑transfer coefficient for conduction through the gas in the fuel-cladding gap is given by
(8.3‑137)
where
\(h_{\text{g}}\) = Conduction heat-transfer coefficient, W m-2 K-1
\(k_{\text{g}}\) = Thermal conductivity of the gas in the gap, W m-1 K-1
\(\left( \Delta r \right)_{\text{g}}\) = Total effective fuel-cladding gap size, m
The conductivities of the helium and xenon gases that comprise the mixture in the fuel‑cladding interface are given in Section 8.7.11 and Section 8.7.12. The conductivity of this mixture of gas is derived from the kinetic theory of gases [8‑20].
(8.3‑138)
(8.3‑139)
where
\(k_{\text{g}}\) = Thermal conductivity of mixture of gases, W m-1 K-1
\(k_{\text{i}}\) = Thermal conductivity of pure gas component \(i\), W m-1 K-1
\(X_{\text{i}}\) = Mole fraction of pure gas component \(i\)
\(M_{\text{i}}\) = Atomic weight of pure gas component \(i\)
For the assumed binary mixture of helium and xenon, Eqs. 8.3-138 and 8.3-139 can be made specific with the subscripts \(h\) and \(x\) referring to the helium and xenon, respectively.
(8.3‑140)
(8.3‑141)
(8.3‑142)
The effective gap size in Eq. 8.3-137 contains three elements based on the fuel‑cladding gap considerations illustrated in Figure 8.3.1. The first is the nominal fuel‑cladding gap size. If the fuel and cladding are in contact this value goes to zero. The second consideration is derived from the incomplete energy exchange between the gas atoms and the solid surface of the fuel or cladding. This is modeled as an addition to the gap size. The third consideration is derived from the effects of surface roughnesses. Since the surfaces are not perfectly smooth, the roughness will produce a residual gap through which conduction takes place, as illustrated in Figure 8.3.1.
(8.3‑143)
where
\(g_{\text{c}}\) = Thermal jump distance of the cladding surface, m
\(g_{\text{f}}\) = Thermal jump distance of the fuel surface, m
\(\delta_{\text{c}}\) = Mean surface roughness of the cladding, m
\(\delta_{\text{f}}\) = Mean surface roughness of the fuel, m
\(C\) = Interface pressure dependent factor
The formulation for the temperature jump distances is derived from the kinetic theory of gases [8‑20]. The jump distance is directly proportional to the mean free path of the gas in the gap. The extent to which energy exchange occurs when a gas atom strikes the solid surface is defined as the accommodation coefficient, \(a\). This coefficient depends on the species present in the gas, and in the case of a mixture of monoatomic gases is determined from
(8.3‑144)
where
\(a_{\text{mix}}\) = Accommodation coefficient of the gas mixture
\(a_{\text{i}}\) = Accommodation coefficient of the \(i\)-th species of gas in the mixture
\(X_{\text{i}}\) = Mole fraction of the \(i\)-th species of gas in the mixture
\(M_{\text{i}}\) = Molecular weight of the \(i\)-th species of gas in the mixture
With the conductivity of the mixture, \(k_{\text{g}}\), defined in Eq. 8.3-142, the jump distance, \(g\), is determined from
(8.3‑145)
where
\(g\) = Jump distance of the surface under consideration, m
\(R_{\text{m}}\) = Gas constant of the gas mixture, J K-1
\(\gamma\) = Ratio of heat capacity at constant pressure to the heat capacity at constant volume
\(C_{\text{v}}\) = Heat capacity at constant volume, J kg-1 K-1
\(P_{\text{g}}\) = Gas pressure in the gap, Pa
From the above equation applied to the fuel and cladding surfaces, the second term in Eq. 8.3-143 can be determined.
The third term concerns the surface roughnesses of the cladding and fuel. The parameter, \(C\), is assumed to depend exponentially on the interface pressure and is given by
(8.3‑146)
where
\(C_{\text{o}}\) = Input pre-exponential constant, \(\sim 1.98\)
\(P_{\text{i}}\) = Fuel-cladding interface pressure, Pa
This formulation was determined for use in the GAPCON code [8‑19] from the data from Ross and Stoute [8‑18]. The value of C is then multiplied by the sum of the mean surface roughnesses of the cladding and the fuel to generate the component of the effective gap resulting from the mismatch of the surface roughnesses. As the interface pressure increases, this gap component becomes smaller because the increased pressure forces a more intimate contact between the surfaces.
8.3.8.1.3. Solid-to-solid Heat Transfer¶
In addition to conduction through the gap and radiative heat transfer, heat can be passed directly through the solid‑to‑solid contact points when the gap is closed. Lassmann and Pazdera [8‑21] suggest that the coefficient can be described by the following correlation:
(8.3‑147)
where
\(A,m\) = Constants determined through experimental comparisons
\(k_{\text{s}}\) = Effective thermal conductivity, W m-1 K-1
\(H\) = Hardness of the softer of the two materials, Pa
\(R\) = Square root of the mean squared roughnesses, m
The effective solid conductivity, \(k_{\text{s}}\), is defined by
(8.3‑148)
where
\(k_{\text{c}}\) = Thermal conductivity of the cladding at the inner surface, W m-1 K-1
\(k_{\text{f}}\) = Thermal conductivity of the fuel at the outer surface, W m-1 K-1
The square root of the mean squared surface roughnesses, \(R\), is defined by
(8.3‑149)
The softer of the two materials is usually the cladding, however, depending on the transient conditions it could be either. Therefore, correlations for both the cladding and fuel have been incorporated, see Section 8.7.13 and Section 8.7.14. The lower of the two values is used in Eq. 8.3-147.
The values of the constants A and m have been determined by Lassmann and Pazdera [8‑21] through comparisons with experimental information to be 0.638 for A and 0.67 for m.
8.3.8.1.4. Total Gap Heat-transfer Coefficient¶
The total heat‑transfer coefficient across the fuel‑cladding interface is the sum of the three components discussed above.
(8.3‑150)
If the fuel and cladding are not in contact, then the solid‑to‑solid term is set to zero.
The gap conductance is a parameter that both affects and is affected by changes in the temperatures, dimensions, and gas composition of the fuel-cladding gap. Because of this, the only way to achieve a fully consistent state between the gap conductance, dimensions, and temperatures is through a series of iterations. First an estimate of the gap conductance would be made. Second, the thermal changes for the time step would be calculated. Third, the dimensional and phenomenological changes over the time step would be determined. Fourth, the new state would be used to calculate a new gap conductance. If the initial estimate and the final value agreed within some predetermined error bound, the gap conductance is said to be consistent with the thermal/mechanical state. If the resultant gap conductance was outside the allowed error band, a new estimate would be determined and the entire calculation redone.
While this iteration method would achieve strict consistency, it can lead to long running times for a computer code. Because SAS4A must perform its calculations over many channels and long time periods, it is not possible to use the computational time necessary for the above scenario. Instead, two approximations are used. First, the effect of the new gap conductance estimate on the fuel surface gap temperature is considered. Within the function routine HGAP, iterations are performed over successive estimates of the conductance until the resulting gap conductance value is consistent with the estimated fuel surface temperature for that conductance value, and the resultant fuel and gas conductivities. No dimensional changes are considered, only conductivity effects.
The second method of adjustment has also been employed to smooth the transition between time steps. The new value of gap conductance passed to the thermal routines of SAS4A is an average of the new calculated value and the previous time step value. Experience has shown that using the new calculated value leads to oscillations in the temperatures and dimensions, while this averaging technique produces smoother transitions. In the pre‑transient calculation this procedure usually produces less than a 2% difference between the calculated and used gap conductances. This can become much larger during pretransient power changes, but the values reconverge quickly after a new constant level is attained. The differences are primarily due to dimensional changes not considered in HGAP. In the transient state, the time steps are so short that the dimensional changes are small, resulting in less than a 1% difference in the calculated and used values of gap conductance. These differences are quite acceptable, especially when weighed against the large savings in computational effort.
A final check is made to see if the new value is between the minimum and maximum values allowed, which are input parameters. If the calculated value is outside the bounds, then the appropriate bound is used as the new value. This is useful if a constant gap conductance is required in order to study parametric effects from other models. In ordinary circumstances, these bounds should be set very wide to allow the model to calculate its own value and not be restricted.
8.3.8.2. SAS3D Parametric Model¶
In the SAS3D code [8‑22], a parametric model was employed to determine the gap conductance. This equation is based on the consideration that the gap conductance has some minimum value plus a term that is related to the fuel-cladding gap size and the gas conductivity.
(8.3‑151)
where
\(c_{1}\), c_{2}`, c_{3}` = Constants
\(r_{\text{c}}\) = Inner cladding radius, m
\(r_{\text{f}}\) = Outer fuel radius, m
The second term on the right‑hand side of Eq. 8.3-151 approximates the conduction term in the model discussed above (see Section 8.3.8.1.2). If the fuel and cladding are in contact, there still exists a residual gap through which conduction occurs, i.e., \(c_{3}\) in Eq. 8.3-101. By dividing the numerator and denominator of this conduction term by the constant \(c_{2}\), the equation form coded in the function HBFND is developed.
(8.3‑152)
where
\(A,B,C,H\) = Input empirical constants
While this model does resemble parts of the model described in Section 8.3.8.1, it also has disadvantages. It is only dependent on the gap size and there is no ability to model the effects of solid‑to‑solid contact or temperature and gas mixture effects on gas conductivity. Its inclusion in SAS4A does allow for a comparison with SAS3D results while using the same gap conductance parameters.
The values calculated by this model are also restricted by upper and lower bounds.
8.3.8.3. SAS3D Simple Model¶
The final model depends only on the fuel‑cladding gap size. It is included for parametric comparisons with previous SAS3D results. If there is no fuel‑cladding gap, the upper bound on the gap conductance is used. If a gap does exist, the conductance is calculated from
(8.3‑153)
where
\(H\) = Input constant, W m-1 K-1
\(r_{\text{c}}\) = Inner cladding surface radius, m
\(r_{\text{f}}\) = Outer fuel surface radius, m
If this value falls below the lower bound, the lower bound is used for the next thermal calculation.
8.3.9. Fuel Axial Expansion Reactivity Model¶
One of the important reactivity feedbacks in reactor safety analysis is the density change caused by the thermal expansion of the fuel and cladding of the pin. Because the magnitude of this effect can depend on the conditions existing at the fuel-cladding interface, a number of options were made available in DEFORM to study this phenomenon. In the previous release version of SAS4A several options were made available; (1) the fuel could be assumed to expand freely, (2) the fuel could be assumed to be constrained against the cladding requiring a force balance between the fuel and cladding, and (3) a mixture of the two could be assumed depending the actual fuel-cladding conditions.
Results from experiments carried out in RAPSODIE [8-23] with oxide fuel have indicated another possibility. Modifications have been made to the EXPAND subroutine of DEFORM to allow for the inclusion of the assumption that the fuel expansion is controlled by the cladding expansion.
If the DEFORM‑4 module is used in a calculation, it will perform the calculation for the transient mass redistribution effects from the axial expansion of the fuel and cladding. It is assumed that the fuel and cladding masses within an axial segment remain constant throughout the transient DEFORM‑4 calculation. Although axial expansion is calculated for both the upper and lower axial blankets, as well as the active core region, the fuel reactivity is calculated only over the axial segments in the active core region. It is also assumed that the location of the bottom interface of the lower axial blanket does not change. All elevation changes are related to this fixed location.
8.3.9.1. Free Fuel Expansion Controlled Feedback¶
If the fuel and cladding are assumed to behave independently of each other because of an open fuel-cladding gap or interface conditions that allow the fuel to slip freely along the cladding, the reactivity feedback from axial expansion of the pin will be dominated by the thermal expansion, and thus the temperatures, of the fuel. In oxide fuels where the thermal conductivity of the fuel is low and the fuel-cladding gap conductance is low, this assumption effectively decouples the fuel response from the coolant or cladding temperatures and directly relates the reactivity feedback to the power level.
The consequence of this assumption for TOP transients is an increased negative feedback as the power level increases. In a loss of flow (LOF) transient where the power level may drop during the initial stages, there would be a positive reactivity addition due to the cooling of the fuel as the power decreased. In later stages when boiling produces larger positive reactivity additions, the expansion reactivity would again become negative, particularly during a transient-over-power (TOP) event.
The metal fuel pins would behave in much the same manner, except on a more reduced scale. The high thermal conductivity of the fuel and sodium in the gap produces a much closer coupling between the fuel and coolant temperatures.
8.3.9.2. Free Cladding Expansion Controlled Feedback¶
The opposite assumption to that discussed in Section 8.3.9.1 above would be to assume that the expansion of the cladding controlled the axial movement of the fuel. The condition necessary for this to be plausible would be an oxide fuel that contains many transverse cracks and fuel connected to the cladding, or a metal fuel connected to the cladding that contains no strength to resist the cladding changes. Some tests and analyses performed with the RAPSODIE reactor [8-23] seem to indicate this type of behavior for oxide fuel.
The consequence of this assumption is to connect the fuel expansion feedback with the coolant, and thereby cladding, temperatures and decouple the feedback from the power level except through its affect on the coolant temperatures. In a TOP scenario, this reduces the magnitude of the reactivity feedback significantly. In the early stages of a LOF event, the effect is to change the magnitude and sign of the feedback from that discussed in Section 8.3.9.1. The feedback would actually be negative as the feedback reached an asymptotic level in a fully voided channel. Differences in magnitude would again occur between the metal and oxide fuels due to the rate of energy transfer to the coolant and the different thermal expansion properties.
This assumption was not included in original version of the SAS4A code but has been added. Since DEFORM calculates both the cladding and fuel response separately under the free expansion assumption (see Section 8.2.4) this assumption was easily added by allowing the cladding expansion to control the expansion of the axial segments.
8.3.9.3. Constrained Fuel/Cladding Expansion Controlled Feedback¶
The final option available in DEFORM for the calculation of the axial expansion assumes that the fuel and cladding are locked together. The expansion is then determined from the required force balance at the fuel-cladding interface. This model is discussed in Section 8.2.4.
Unlike either of the two previous options, this one requires that both the fuel and cladding responses to the specified transient be considered. It would be expected that the results from these assumptions would fall somewhere between those of the previous two sections since elements of both are included in the considerations. In practice this has been found to be the case. In situations where the fuel and cladding can be assumed to be in contact, such as high burnups with low swelling cladding or medium burnups with the metal fuels, this option would be expected to yield the most credible results. Even when the oxide fuel can be assumed to be heavily cracked, this option may be most accurate because the bowing or twisting of the pin due to the interaction with wire step may cause the cracked fuel to be wedged within the cladding and therefore act as constrained rather than following the cladding expansion, particularly if the number of transverse cracks is small compared to the length of the fuel segments or the pellets can be assumed to have sintered together.
8.3.10. Metal Fuel Modeling¶
With the renewed interest in uranium metal fuels for breeder reactor applications, there is a need to provide modeling to handle this type of fuel. An initial effort has been made to include important phenomenological features of the metal fuel. This effort involved the use of available DEFORM modeling and incorporation of necessary material properties. Which this effort is not complete, it does provide a basis for evaluating the consequences of the use of metal fuel.
8.3.10.1. Fission Gas Behavior¶
The buildup of fission gas within the metal fuel produces considerably more fuel swelling than is seen in oxide fuels. In oxide fuels, the strength of the fuel matrix is such that the fission gas bubbles remain small during the irradiation. There is collection of gas on grain boundaries, which leads to fuel swelling, and boundary bubble connecting which produces a local “tunneling” effect that leads to fission gas release.
Recent studies on the growth mechanisms in the analyses of metal fuel swelling [8-24] have indicated that the transient swelling is dominated by grain boundary bubbles, so a single bubble model in an amorphous medium would not be adequate. These grain boundary bubbles also appear to be important for the development of the interlinked porosity in metal fuels. The early work with metal fuels allowed for only low-burnup irradiations because of the extensive swelling, but once it was determined that this “breakway” swelling appeared to be self-limiting, and if enough space was fabricated into the fuel-cladding gap, the result was very little stress on the cladding and high burnups could be achieved [8-25, 8-26]. In order to calculate the steady state behavior of the metal fuel, it is therefore necessary to model this swelling and associated gas release in a consistent manner.
The study of this phenomenon is still underway and not yet developed to the state where an appropriate model could be developed for inclusion into DEFORM. It was therefore necessary to use a more empirical model based on the observed relationship between fuel swelling and fission gas release.
8.3.10.1.1. Closed and Connected Porosity Description¶
Initially, all created fission gas is assumed to go into fission gas bubbles within the fuel matrix. These bubbles are then allowed to swell in response to any overpressure produced by the bubble pressure acting against the surface tension and hydrostatic pressure [8-27, 8-28]. The amount of swelling allowed is controlled by a time constant determined from the creep rate of the fuel in response to the bubble overpressure. This produces a system of closed porosity within the fuel matrix. The modeling for this creation of closed porosity already existed in DEFORM and the modifications made were to introduce the correct material properties for the metal fuel.
As the closed porosity fraction increases, a point is reached where release would occur. It is assumed that fission gas release is associated with the formation of connected porosity. The release fraction defines the amount of porosity and fission gas that is transferred from closed to open porosity. The calculation of open porosity changes is tied directly to the fission gas release calculation and is explained in more detail below.
8.3.10.1.2. Fission Gas Release¶
The calculation for the amount of fission gas released from the closed porosity is determined directly from the swelling of the fuel cell. First the volumetric swelling fraction is determined from the fully dense theoretical volume and the actual cell volume, which includes porosity.
(8.3‑154)
where
\(S_{\text{f}}\) = Volumetric swelling fraction
\(V_{\text{c}}\) = Actual volume of the fuel cell, m3
\(V_{\text{th}}\) = Theoretical volume of the mass of fuel in the cell, m3
By fitting the swelling vs gas release data from Ref. 8-25 and 8-26, see Figure 8.3.3 the following equation was generated, defining the gas release fraction \(R_{\text{f}}\). A least 22.78% swelling is required before the gas is released.
(8.3‑155)
where
\(R_{\text{f}}\) = Fraction of total fission gas released
Figure 8.3.3 Effect of Fuel Swelling on Fission Gas Release in Metal Fuels¶
The total amount of gas released ins therefore the release fraction from Eq. 8.3-155 time the total generated in the node. The amount released during a computational time step is the difference between the total released and the amount released previously.
(8.3‑156)
where
\(G_{\text{r}}\) = Gas released during the time step, kg
\(G_{\text{t}}\) = Total amount of gas produced in the cell, kg
\(G_{\text{f}}\) = Gas retained in the fuel assuming no release during the time step, kg
It is then assumed that the release of this amount of gas moves an equivalent fraction of the closed porosity volume to the open porosity.
(8.3‑157)
where
\(V_{\text{r}}\) = Volume moved from closed to open porosity, m3
\(V_{\text{f}}\) = Volume of fission gas in closed porosity, m3
These calculations are carried out in the subroutine RELGAS.
8.3.10.2. Metal Fuel Behavior During Melting¶
8.3.10.2.1. Molten Cavity¶
The melting of a cell begins as the temperature reaches an input determined temperature, between the solidus and liquidus temperatures. The incremental melt fraction approach developed in Section 8.3.7 is then used to move fuel, gas, and volumes between the solid and molten state. As the temperature of the cell rises above the initial melting temperature, the temperature of the cell rises above the initial melting temperature, increasing fractions of the cell become associated with the molten cavity. When the cell temperature reaches the fuel liquidus temperature, the whole cell is associated with the molten cavity. Since each radial cell is treated separately, an annular melt zone would be correctly treated if it existed in a U-Pu-Zr fuel pin.
8.3.10.2.2. Connected Porosity¶
Upon melting the connected porosity is released to the molten cavity instantaneously. It is assumed that the bubble morphology associated with this interlinked porosity is such that upon melting, there is no time delay between melting and release of the gas and associated volume to the molten cavity free volume. The connected porosity acts in the same manner as the grain boundary gas in the oxide fuel as far a melting is concerned see Section 8.3.7.2.2. Table 8.3.1 illustrates the similarities and difference between the types of gas associated with the metal fuel and those of the oxide fuel.
8.3.10.2.3. Closed Porosity¶
The closed porosity consisting of fission gas in constrained bubbles is assumed to act like the retained gas in the oxide fuel. Upon melting, these bubbles must move to the free volume in order to coalescence into the molten cavity. This is treated through the use of a time constant for bubble coalescence. Only the retained gas in the molten fuel can undergo this coalescence process (see Section 8.3.7.2.3). Recent results with the model have indicated a need for further refinement by breaking this closed porosity into an intragranular component and a grain boundary component that would be released immediately on melting.
Behavior |
Oxide Fuel Porosity |
Metal Fuel Porosity |
Causes fuel swelling |
Grain boundary |
Closed |
Released immediately to molten cavity when fuel melting |
Grain boundary |
Connected |
Release to molten cavity other coalescence delay |
Intra-granular |
Closed |
8.3.10.3. Axial Extrusion in Solid Fuel¶
One of the reasons for interest in metal fuels is the possibility for axial relocation within the intact cladding. While recent preliminary experimental evidence from the TREAT M2 and M3 tests [8-29] indicate that axial relocation occurs primarily upon fuel melting, the study of solid fuel swelling and extrusion possibilities are valuable for they add to the understanding of the fundamental properties of metal fuel. These phenomena include porosity formation and behavior, fuel creep, fission gas swelling, and fuel-cladding chemical interaction.
8.3.10.3.1. Fission Gas Induced Swelling¶
DEFORM, for both oxide and metal fuel, calculates the increase or decrease in bubble volume containing trapped fission gas in response to the bubble pressure, the local hydrostatic pressure, the bubble surface tension, and the fuel creep rate. This is described in Section 8.3.4 for the oxide fuel.
In the metal fuel the porosity is divided into open and closed porosity, as described in Section 8.3.10.1.1 above, with the closed porosity assumed to produce the fuel swelling. The same basic approach adopted for the oxide fuel is used for the metal fuel swelling modeling. The amount of retained fission gas and the volume available at the beginning of a time step determine the gas pressure in the closed porosity. This force is counteracted by the local hydrostatic pressure and the bubble surface tension. The mismatch between the bubble pressure and restraining forces is the driving force for expansion (bubble pressure greater than restraining pressure) or contraction (bubble pressure less than restraining pressure) of the closed porosity. If the bubble pressure is the same as the restraining pressure, a state of equilibrium would exist. Therefore, given that the amount of retained gas and the restraining pressure are known, an equilibrium closed porosity volume can be determined that would give a bubble pressure equal to the restraining pressure. This is the volume the closed porosity will tend towards during the time step. However, an instantaneous volume change does not occur because the fuel has a finite creep rate dependent on the mismatch between the initial bubble pressure and restraining pressure, the fuel temperature, and the fission rate. This creep rate defines a time constant associated with the change in bubble volume. The time constant and the current computational time step determine the magnitude of the volume change that takes place as the bubble volume changes from its current volume toward the equilibrium volume.
In the development of the model for the metal fuel, it was found that one of the most sensitive parameters influencing the fuel swelling was the fission gas bubble size used to calculate the surface tension. Because of the low strength of the metal fuel, and the assumption that the interlinked porosity is connected to the fission gas plenum, the stress state in the fuel is assumed to equal the plenum pressure. Under these conditions the surface tension restraint becomes a critical parameter in the control of fuel swelling. If bubble sizes are small, the surface tension is high and effectively limits the amount of swelling. If bubble sizes are large, then the bubbles expand rapidly to near equilibrium values, introducing rapid swelling of the fuel.
Because there currently exists little information on the development of bubble morphology during the early irradiation of metal fuels, it was necessary to devise a method of providing a bubble size that produced results consistent with the observation that the fuel-cladding gap closes, in metal fuel pins, in the 2-3 atom percent burnup range. This was achieved by providing a bubble radius dependent on the burnup level and then determining a calibration constant to obtain the desired behavior.
(8.3‑158)
where
\(R_{\text{B}}\) = Fission gas bubble radius of closed porosity, m
\(C_{\text{R}}\) = Calibration constant
\(B\) = Burnup, atom percent
While this formulation does not fully adhere to the principle of using mechanistic models employed in DEFORM, it does produce a reasonable initiation to the calculation and provides for development of other models in a consistent fashion.
8.3.10.3.2. Axial Swelling Fraction¶
Section 8.3.4.1 gives the development of the plane axial swelling strain used in DEFORM. This sam approach is used when considering the metal fuels. However, when the metal fuel comes into contact with the cladding, it is assumed that the fuel strength is not great enough to cause fuel-cladding mechanical interaction. Instead, the volume must be added through axial elongation if the fuel-cladding interface is in such a state that movement can occur, i.e., the temperature of the fuel-cladding interface is above the local eutectic temperature. This movement restriction does not currently exist in DEFORM, but will be operational when DEFORM and SSCOMP are coupled.
After the initial calculation in FSWELL, the outer fuel radius may be greater than the inner cladding radius. The volume that must be accounted for by extra axial expansion is determined by the mismatch between the locations of these two surfaces.
(8.3‑159)
where
\(\Delta V_{\text{exc}}\) = Volume of fuel outside the allowed volume, m3
\(A_{\text{H}}\) = Axial segment height including all strains, m
\(r_{\text{fo}}\) = Outer radius of the fuel including all strains, m
\(r_{\text{ci}}\) = Inner radius of the cladding including all strains, m
The total volume change calculated to take place radially and that calculated to take place axially, from the initial calculation, are then modified by this volume discrepancy of Eq. 8.3-159
(8.3‑160)
(8.3‑161)
where
\(\Delta V_{\text{r,n}}\) = New total change in radial volume, m3
\(\Delta V_{\text{r,o}}\) = Old total change in radial volume, m3
\(\Delta V_{\text{a,o}}\) = New total change in axial volume, m3
\(\Delta V_{\text{a,o}}\) = Old total change in axial volume, m3
These are then used to calculate the new fraction of volume change taking place axially.
(8.3‑162)
where
\(F_{\text{as}}\) = Fraction of volume change taking place axially
This new factor is then used to determine the radial and axial volume changes for each radial cell, and a new generalized axial swelling strain is calculated following the procedure in Section 8.3.4.1. The new node structure is then determined and the fuel and cladding surfaces are again examined. If a mismatch again occurs, the procedure is repeated until a match is formed within a tolerance of 1.0 x 10-12 m. This procedure converges within three to five iterations. Separate thermal/mechanical and swelling strains are maintained for the purpose of comparison. Those calculations are performed in the subroutine FSWELL.
8.3.10.4. Sodium Bond¶
As the fuel-cladding gap changes, the liquid sodium that fills this gap must move to other locations. A new subroutine, NABOND, has been developed which carries out the accounting of the available volumes and calculates the sodium slug level in the plenum. The temperature of the sodium at a particular elevation is assumed to be the average of the fuel and cladding surface temperatures. The mass of sodium at each axial location is determined from the gap volume and sodium density.
(8.3‑163)
where
\(M_{\text{s,j}}\) = Mass of sodium in fuel-cladding gap at axial segment \(j\), kg
\(\rho_{\text{s,j}}\) = Density of liquid sodium at axial segment \(j\), kg/m3
The total sodium mass in the gap is then determined by summing over all axial segments.
(8.3‑164)
where
\(M_{\text{st}}\) = Total mass of sodium in fuel-cladding gap, kg
\(MZ\) = Total number of axial segments in the pin
The sodium mass in the plenum is then found by subtracting the result of Eq. 8.3-164 from the total sodium initially loaded into the pin.
(8.3‑165)
where
\(M_{\text{sp}}\) = Mass of bond sodium in the plenum, kg
\(M_{\text{sl}}\) = Mass of bond sodium initially loaded in the pin, kg
The sodium level in the plenum is then determined.
(8.3‑166)
where
\(H_{\text{sp}}\) = Height of sodium in the plenum, m
\(\rho_{\text{sp}}\) = Density of sodium at the plenum temperature, kg/m3
\(r_{\text{p}}\) = Inner cladding radius in the plenum, m
In the calculation of the plenum pressure, this sodium filled volume is removed from the plenum volume available for the released fission gas. The amount released during a computational time step is the difference between the total released and the amount released previously.