5.3.4. Pumps

Pump components are an extension of the pipe components, in terms of hydraulic contributions. Pump components add the impact of the pump head to the pipe hydraulic contributions, \(\Delta a_{0}^{\text{pipe}}\), \(\Delta a_{1}^{\text{pipe}}\), \(\Delta a_{2}^{\text{pipe}}\), and \(\Delta a_{3}^{\text{pipe}}\), defined in Eq. (5.3-29), Eq. (5.3-40), Eq. (5.3-41) and Eq. (5.3-44), respectively. There are three pump choices available in the PRIMAR-4 module: a user-supplied table look-up, a centrifugal pump, and an electromagnetic pump. There are a number of options for the centrifugal and electromagnetic pumps.

5.3.4.1. Table Look-Up

The user supplies a table of relative pump head vs. time, and the code interpolates linearly between points in the table. The pump head as a function of time is given by

(5.3-49)\[H\left( t \right) = H_{\text{r}} f\left( t \right)\]

where \(f \left( t \right)\) is the user-supplied table, with \(f \left( t = 0 \right) = 1.0\), and \(H_{\text{r}}\) is the reference pump head for the particular pump. The contribution to the coefficients in Eqs. 5.2-10, 5.2-12, 5.2-14, and 5.2-16 are

(5.3-50)\[\Delta a_{0} = \Delta a_{0}^{\text{pipe}}\]

(5.3-51)\[\Delta a_{1} = \Delta t H\left( t_{3} \right) + \Delta a_{1}^{\text{pipe}}\]

(5.3-52)\[\Delta a_{2} = \Delta t \left\lbrack H\left( t_{4} \right) - H \left( t_{3} \right) \right\rbrack + \Delta a_{2}^{\text{pipe}}\]

(5.3-53)\[\Delta a_{3} = \Delta a_{3}^{\text{pipe}}\]

where

\(\Delta t\) = the time interval

\(t_3\), \(t_4\) = the times at the beginning and end of the time interval

5.3.4.2. Centrifugal Pumps

5.3.4.2.1. Option 1

In this option, the pump head and the pump torque are represented either by constant values or by polynomial fits, depending upon the pump flow rates or upon the pump speeds. The flow rates and speeds, and also the pump head and torque, are expressed as multiples of rated quantities, which are user-supplied. The constant values and the coefficients in the polynomial fits are also user-supplied.

The pump head and torque are expressed as functions of the parameter \(\chi\), which is

(5.3-54)\[\chi = \frac{\overline{w}}{\overline{s}}\]

with

(5.3-55)\[\overline{w} = \frac{w}{w_{\text{R}}}\]

(5.3-56)\[\overline{s} = \frac{s}{s_{\text{R}}}\]

where

\(w\) = the pump flow rate

\(w_{\text{R}}\) = the rated pump flow rate

\(s\) = the pump speed

\(s_{\text{R}}\) = the rated pump speed

Pump Head

For positive pump speeds the pump head is taken as

(5.3-57)\[ \begin{align} \Delta p_{\text{p}} = H_{\text{R}} s^{2} \left( A_{1} + A_{2} \chi + A_{3} \chi^{2} + A_{4} \chi^{3} + A_{5} \chi^{4} \right) , && \text{if } \chi < A_{6} \end{align}\]

(5.3-58)\[ \begin{align} \Delta p_{\text{p}} = H_{\text{R}} A_{7} {\overline{w}}^{2} , && \text{if } \left| \chi \right| > A_{6}\text{ and }\overline{w} \geq A_{18} \end{align}\]

(5.3-59)\[ \begin{align} \Delta p_{\text{p}} = - H_{\text{R}} A_{8} {\overline{w}}^{2} , && \text{if } \left| \chi \right| > A_{6}\text{ and }\overline{w} < - A_{18} \end{align}\]

(5.3-60)\[ \begin{align} \Delta p_{\text{p}} = H_{\text{R}} A_{7} \overline{w} A_{18} , && \text{if }\left| \chi \right| > A_{6} \text{ and } A_{18} > \overline{w} \geq 0 \end{align}\]

(5.3-61)\[ \begin{align} \Delta p_{\text{p}} = - H_{\text{R}} A_{8} \overline{w} A_{18} , && \text{if }\left| \chi \right| > A_{6} \text{ and } 0 > \overline{w} \geq - A_{18} \end{align}\]

where

\(\Delta p_{\text{p}}\) = the pump head

\(H_{\text{R}}\) = the reference pump head

\(A_1\) ,… \(A_8\) = user-supplied coefficients

For negative pump speeds, or flow reversal, the pump head is taken as

(5.3-62)\[\begin{split}\Delta p_{\text{p}} = \begin{cases} H_{R} A_{7} d_{1}^{2} & \text{if }d_{1} \geq 0 \\ H_{R} A_{8} d_{1}^{2} & \text{if }d_{1} < 0 \end{cases}\end{split}\]

with

\[d_{1} = \overline{w} - A_{10}\overline{s} ,\]

where

\(A_{10}\) = user-supplied coefficient

Pump Torque

Next, for positive pump speeds, the pump torque is

(5.3-63)\[ \begin{align} \overline{\tau} = {\overline{s}}^{2}\left( A_{11} + A_{12} \chi + A_{13}\chi^{2} + A_{14}\chi^{3} + A_{15}\chi^{4} \right), && \text{if } \left| \frac{\overline{w}}{\overline{s}} \right| \leq A_{6} \end{align}\]

(5.3-64)\[ \begin{align} \overline{\tau} = A_{16}{\overline{w}}^{2} , && \text{if } \left| \frac{\overline{w}}{\overline{s}} \right| > A_{6},\ \overline{w} \geq 0 \end{align}\]

(5.3-65)\[ \begin{align} \overline{\tau} = A_{17}{\overline{w}}^{2} , && \text{if } \left| \frac{\overline{w}}{\overline{s}} \right| > A_{6},\ \overline{w} < 0 \end{align}\]

with

(5.3-66)\[ \overline{\tau} = \frac{\tau}{\tau_{\text{R}}}\]

where

\(\tau\) = the pump torque

\(\tau_{\text{R}}\) = the reference pump torque

\(\chi,\ \overline{w},\ \overline{s}\) = the same as for the pump head

\(A_{11}\), … \(A_{15}\) = user-supplied coefficient

For negative pump speeds, the pump torque is taken as

(5.3-67)\[ \begin{align} \overline{\tau} = A_{16}\left( \overline{w} - A_{20}\overline{s} \right)^{2} , && \text{if } \overline{w} \geq A_{20}\overline{s} \end{align}\]

(5.3-68)\[ \begin{align} \overline{\tau} = A_{17}\left( \overline{w} - A_{20}\overline{s} \right)^{2} , && \text{if } \overline{w} < A_{20}\overline{s} \end{align}\]

Pump Speed

The pump speed and pump torque are related by the equation is

(5.3-69)\[ I \frac{\text{ds}}{\text{dt}} = \tau_{\text{m}} - \tau_{\text{p}} - k_{1} w\]

where

\(I\) = the moment of inertia of the pump and motor

\(s\) = the pump speed

\(\tau_{\text{m}}\) = the motor torque

\(\tau_{\text{p}}\) = the pump torque

\(k_1\) = constant of proportionality

\(w\) = the pump flow rate

The term \(- k_1\) w is a drag term proportional to the flow rate. The motor torque \(\tau_{\text{m}}\) is a user-supplied table look-up.

Rotor Lock-Up

If the normalized pump speed, \(\overline{s}\), falls below the value \(A_9\), and if \(A_9 > 0\), then the rotor locks; and the speed is held at zero after that.

Flow Rate Coefficients

The contribution to the \(a\)’s in Eqs. 5.2-10, 5.2-12, 5.2-14 and 5.2-16 are then as follows:

(5.3-70)\[ \Delta a_{0} = \Delta a_{0}^{\text{pipe}}\]

(5.3-71)\[ \Delta a_{1} = \Delta p_{\text{p}} + \Delta a_{1}^{\text{pipe}}\]

(5.3-72)\[\begin{split} \Delta a_{2} &= \left( \Delta t \right)^{2} \frac{\partial \Delta \text{p}_{\text{p}}}{\partial \text{t}} + \Delta a_{2}^{\text{pipe}} \\ &= \left( \Delta t \right)^{2} \frac{\partial \Delta \text{p}_{\text{p}}}{\partial \text{s}} \frac{\partial \text{s}}{\partial \text{t}} + \Delta a_{2}^{\text{pipe}}\end{split}\]

(5.3-73)\[ \Delta a_{3} = \Delta t \frac{\partial}{\partial \text{w}} \Delta p_{\text{p}} + \Delta a_{3}^{\text{pipe}}\]

\(\Delta p_{\text{p}}\) = the pump head

\(\frac{\partial\mathrm{\Delta p_{\text{p}}}}{\partial \text{t}}, \frac{\partial \text{s}}{\partial \text{t}} \frac{\partial \mathrm{\Delta p_{\text{p}}}}{\partial \text{w}}\) = the partial derivatives of pump head and pump speed described above under the various conditions of speed and flow

5.3.4.2.2. Option 2

This pump option makes use of the homologous pump curves and permits operation of the pump in all four quandrants of pump operations – normal pump mode, energy dissipation mode, turbine mode, and reverse pump mode. In homologous pump theory, the homologous curves depict the pump performance map which relates the pump output variables to its input variables. The homologous curves are valid for a class of pumps that are geometrically and dynamically similar, independent of the fluid. The basis is that the physical parameters that describe the pump geometry, the fluid conditions, and the operating performance are functionally related. Therefore performance data acquired from a test or prototype pump can then be applied to predict the performance of other “similar” pumps. Default curves used for the pump head and torque are built into the model using data statements and are the three-region curve fit taken from a memo by J. F. Koenig for a pump with a specific speed (\({N_s}\)) of 1800 rpm [5-1]. Users may override the defaults by defining a positive value for IPMDFT, defining polynomial coefficients via PMPHD and PMPTQ, and then selecting those coefficients by defining APMPHD(18).

The pump head and torque values are obtained from

(5.3-74)\[ H = H_{\text{r}} \left( {\overline{w}}^{2} + {\overline{s}}^{2} \right) \sum_{\text{i} = 0}^{6}{C_{\text{ji}} x^{i}}\]

(5.3-75)\[ T = T_{\text{r}} \left( {\overline{w}}^{2} + {\overline{s}}^{2} \right) \sum_{\text{i} = 0}^{8}{D_{\text{ji}} x^{i}}\]

where

\(H\) = pump head

\(T\) = pump torque

\(w\) = flow rate

\(s\) = pump speed

\(x = \pi + \left( \frac{\overline{w}}{\overline{s}} \right) = \pi + \mathrm{atan2}\left( \overline{w},\overline{s} \right)\)

and the bar denotes normalization with respect to reference quantities\(\left( \text{i.e.}, \overline{w} = w/w_{\text{r}} \right)\) and the subscript \(r\) denotes reference quantities. The coefficients \(C_{\text{ji}}\) and \(D_{ji}\) represent the three-region curve fit to a sixth-order polynomial with:

\[\begin{split} j = \begin{cases} 1 & 0 \leq x \leq 3.14159 \\ 2 & 3.14159 < x \leq 4.7124 \\ 3 & 4.7124 < x \end{cases}\end{split}\]

The value for \(H_{\text{r}}\) is an input while \(T_{\text{r}}\) is obtained from

(5.3-76)\[ T_{\text{r}} = \frac{H_{\text{r}} w_{\text{r}}}{\left( s_{\text{r}} \eta \rho \right)}\]

where \(\eta\) is the pump efficiency at reference conditions and \(\rho\) is the fluid density.

The coefficients \(C_{\text{ji}}\) and \(D_{ji}\) are provided in Table 5.3.2 and Table 5.3.3.

Table 5.3.2 Default pump head coefficients for option 2 of the centrifugal pump model.

i	j=1	j=2	j=3
0	0.63381	431.96699	6171.9821
1	0.46016	-576.61438	-4958.9692
2	-2.40040	301.00029	1406.3329
3	3.17937	-75.46586	-126.17344
4	-1.77304	8.67550	-13.21712
5	0.46236	-0.26062	3.24505
6	-0.04625	-0.01596	-0.16925

Table 5.3.3 Default pump torque coefficients for option 2 of the centrifugal pump model.

i	j=1	j=2	j=3
0	-0.68437	-1154.9471	-379.81080
1	2.77599	1858.4915	726.14914
2	-5.39880	-1237.6683	-496.25029
3	6.85412	436.01653	167.64136
4	-4.07579	-85.57377	-30.36692
5	1.08133	8.86277	2.83119
6	-0.10476	-0.37830	-0.10682
7	0.0	0.0	0.0
8	0.0	0.0	0.0

At low flow conditions with \(\left| \overline{w} \right| < w_{\text{c}}\) where \(w_{\text{c}}\) represents a cutoff value specified by the user, the pump head is calculated as a linear interpolation between the pump head at zero flow and at the \(w_{\text{c}}\) flow:

(5.3-77)\[ H \left( w,s \right) = \frac{\left( H \left( {\overline{w}}_{\text{c}},\overline{s} \right) \overline{w} + H\left( 0,\overline{s} \right) \left( w_{\text{c}} - \overline{w} \right) \right)}{w_{\text{c}}}\]

The value \(w_{\text{c}}\) is specified as an input value in APMPHD (13,IPMP) in input block 18. The frictional torque losses, \(T_{\text{f}}\), are taken as a three-region quadratic fit over \(\overline{s}\)

(5.3-78)\[ T_{\text{f}} = T_{\text{r}} \left( A_{\text{j}1} + A_{\text{j}2} \overline{s} + A_{\text{j}3} \overline{s} \left| \overline{s} \right| \right)\]

where

\[\begin{split} j = \begin{cases} 1 & \overline{s} < s_{1} \\ 2 & s_{1} < \overline{s} < s_{2} \\ 3 & s_{2} < \overline{s} \end{cases}\end{split}\]

The nine coefficients, \(A_{\text{ji}}\), are specified as input values in APMPHD. The cutoff speeds \(s_1\) and \(s_2\) are also input values in APMPHD. The recommended values for the nine coefficients and cutoff speeds are presented in Table 5.3.4.

Table 5.3.4 Recommended values for the torque loss coefficients in option 2 for the centrifugal pump.

k	Variable	APMPHD(K,IPMP)
1	\(A_{1,1}\)	0.01
2	\(A_{2,1}\)	0.0
3	\(A_{3,1}\)	-73.13
4	\(A_{1,2}\)	0.00268
5	\(A_{2,2}\)	0.0
6	\(A_{3,2}\)	0.07
7	\(A_{1,3}\)	0.00383
8	\(A_{2,3}\)	0.01071
9	\(A_{3,3}\)	0.01406
10	\(s_{1}\)	0.01
11	\(s_{2}\)	0.268

For the steady-state, the subroutine SSPUMP makes use of a root finder to locate the pump speed necessary for a specified pump head. It is assumed that steady-state will be at a flow level above \(w_{\text{c}}\).

The subroutine PUMPFL includes the following calculations for \(\Delta a_{\text{o}}\), \(\Delta a_1\), \(\Delta a_2\) and \(\Delta a_3\), with

(5.3-79)\[ \Delta a_{0} = \Delta a_{0}^{\text{pipe}}\]

(5.3-80)\[ \Delta a_{1} = H + \Delta a_{1}^{\text{pipe}}\]

(5.3-81)\[ \Delta a_{2} = \Delta t^{2} \frac{\partial}{\partial \text{t}}H + \Delta a_{2}^{\text{pipe}}\]

(5.3-82)\[ \Delta a_{3} = \Delta t \frac{\partial}{\partial \text{w}}H + \Delta a_{3}^{\text{pipe}}\]

where \(H\) and \(\Delta t\) represent the pump head and time interval, respectively. The terms \(\Delta a_{\text{o}}\) and \(\Delta a_1\) are calculated as in the centrifugal pump option 1; \(\Delta a_2\) is found using:

(5.3-83)\[ \frac{\partial}{\partial \text{t}}H = \frac{\partial \overline{s}}{\partial \text{t}} \frac{\partial \text{H}}{\partial \text{s}}\]

where

(5.3-84)\[ \frac{\partial \overline{\text{s}}}{\partial \text{t}} = \frac{\left( T_{\text{m}} - T_{\text{p}} - T_{\text{f}} \right)}{\left( s_{\text{r}}I \right)}\]

\(T_{\text{m}}\) = motor torque,

\(I\) = pump inertia

and from Eq. (5.3-73) and Eq. (5.3-76)

(5.3-85)\[ \frac{\partial \text{H}}{\partial \overline{\text{s}}} = 2H_{\text{r}} \overline{s} \sum_{\text{i} = 0}^{6}{c_{\text{ji}} x^{i}} - H_{\text{r}} \overline{w} \sum_{\text{i} = 1}^{6}{c_{\text{ji}} ix^{i - 1}}\]

for \(\left| \overline{w} \right| > w_{c}\text{and}\)

(5.3-86)\[ \frac{\partial \text{H}}{\partial \overline{\text{s}}} = \frac{\left\lbrack \frac{\partial \text{H}}{\partial \overline{\text{s}}} \left( w_{\text{c}},\overline{s} \right) \overline{w} + \frac{\partial \text{H} \left( 0,\overline{s} \right)}{\partial \overline{\text{s}}} \left( w_{\text{c}} - \overline{w} \right) \right\rbrack}{w_{\text{c}}}\]

for \(\left| \overline{w} \right| < w_{\text{c}}\). \(T_{\text{m}}\) is defined using AMOTTK or using JTYPE=-2 within the control system (see Table 2.8.9).

\(\Delta a_3\) is found using Eq. (5.3-82) and

(5.3-87)\[\begin{split}\frac{\partial \text{H}}{\partial \overline{w}} &= 2H_{\text{r}} \overline{w} \sum_{\text{i} = 0}^{6}{c_{\text{ji}}x^{i}} + H_{\text{r}}\overline{s}\sum_{\text{i} = 1}^{6}C_{\text{ji}} ix^{i - 1} \\ \frac{\partial \text{H}}{\partial \text{w}} &= \frac{1}{w_{\text{r}}} \frac{\partial \text{H}}{\partial \overline{\text{w}}}\end{split}\]

for \(\left| \overline{w} \right| > w_{\text{c}}\) and from

(5.3-88)\[ \frac{\partial \text{H}}{\partial \overline{\text{w}}} = \frac{\left( H\left( w_{\text{c}},\overline{s} \right) - H\left( 0,\overline{s} \right) \right)}{w_{\text{c}}}\]

for \(\left| \overline{w} \right| < w_{\text{c}},\) and

The subroutine PUMPFN includes the pump torque curves in integrating Eq. (5.3-84) to determine \(s\). Approximating Eq. (5.3-84) as

(5.3-89)\[ I \frac{\Delta s}{\Delta t} = T_{\text{m}} - \frac{1}{2} \left( T_{3} + T_{4} \right) - \frac{1}{2} \left( T_{\text{f}3} + T_{\text{f}4} \right)\]

Note where the subscripts 3 and 4 denote the beginning and ending times of the \(\Delta t\) interval and approximating

(5.3-90)\[ T_{4} = T_{3} + \frac{\partial \text{T}}{\partial \text{s}} \Delta s + \frac{\partial \text{T}}{\partial \text{w}} \Delta w\]

(5.3-91)\[ T_{\text{f}4} = T_{\text{f}3} + \frac{\partial \text{T}_{\text{f}}}{\partial \text{s}} \Delta s\]

in Eq. (5.3-89), \(\Delta s\) may be obtained as

(5.3-92)\[ \Delta s = \frac{T_{\text{m}} - T_{3} - \frac{1}{2} \frac{\partial \text{T}}{\partial \text{w}} \Delta w - T_{f3}}{\left\lbrack \frac{I}{\Delta t} + \frac{1}{2} \frac{\partial \text{T}}{\partial \text{s}} + \frac{1}{2} \frac{\partial T_{\text{f}}}{\partial \text{s}} \right\rbrack}\]

Locked Rotor

If \(\overline{s} < A_{20}\), where \(A_{20}\) is the input variable APMPHD(20, IPMP), and if \(\overline{w} < A_{19}\), then the rotor locks and the pump speed is set to zero and held at zero. For a locked rotor the pump head is calculated as

(5.3-93)\[\begin{split} H = \begin{cases} - T_{\text{r}} A_{12} w \left| w \right| \geq A_{13} & \text{if }\left| \overline{w} \right| \geq A_{13} \\ - T_{\text{r}} A_{12} A_{13} \overline{w} & \text{if }\left| \overline{w} \right| < A_{13} \end{cases}\end{split}\]

where \(A_{12}\) and \(A_{13}\) are input in the APMPHD(K, IPMP) array.

Pump Cavitation

In a centrifugal pump, cavitation will occur if the applied net positive suction head (ANPSH), or pump inlet pressure, is less than the required net positive suction head (RNPSH). This can occur if there is a break in the outlet pipe from the pump, leading to an increase in the pump flow rate and an increase in the RNPSH. If pump cavitation occurs, there will be a drop in pump head. Although there is reasonably good RNPSH data for many pumps, there is little data on pump behavior in the cavitation range, mainly because cavitation tends to destroy a pump, so no one wants to operate in that range. On the other hand, transient pump cavitation can occur for a short time after a pipe rupture, and the resulting decrease in pump head can have a significant impact on the flow out the rupture and on the flow rate through the core. The homologous pump model in PRIMAR-4 tests for pump cavitation and reduces the pump head if cavitation occurs.

The required net positive suction head is calculated as

(5.3-94)\[ \text{RNPSH} = {\overline{s}}^{2} \left( C_{\text{c}0} + C_{\text{c}1} Z + C_{\text{c}2} Z^{2} + C_{\text{c}3} Z^{3} + C_{\text{c}4} Z^{4} \right)\]

where

(5.3-95)\[ Z = \frac{\overline{w}}{\overline{s}}\]

Then, if RNPSH > ANPSH, the cavitated head, \(H_{\text{c}}\), is calculated as

(5.3-96)\[ H_{\text{c}} = f_{\text{c}} H\]

where \(H\) is the normal head, calculated as described in the previous sections, and the cavitation factor \(f_{\text{c}}\) is calculated as

(5.3-97)\[ f_{\text{c}} = \frac{1}{1 + 1000x^{2}}\]

where

(5.3-98)\[ x = \frac{\text{RNPSH} - \text{ANPSH}}{\text{ANPSH}}\]

The cavitation factor of Eq. (5.3-97) is somewhat arbitrary; but, as previously mentioned, there is little data for behavior in the cavitation range, and this expression results in a rapid drop in pump head as the pump goes farther into the cavitation range. With this treatment, the expressions used in Eq. (5.3-82) and Eq. (5.3-83) for \(\Delta a_2\) and \(\Delta a_3\) are

(5.3-99)\[ \frac{\partial \text{H}_{\text{c}}}{\partial \overline{\text{s}}} = f_{\text{c}} \left\lbrack \frac{\partial \text{H}}{\partial \overline{\text{s}}} - 2000 xH \frac{\partial \text{x}}{\partial \overline{\text{s}}} \right\rbrack\]

(5.3-100)\[ \frac{\partial \text{H}_{\text{c}}}{\partial \overline{\text{w}}} = f_{\text{c}} \left\lbrack \frac{\partial \text{H}}{\partial \overline{\text{w}}} - 2000 xH \frac{\partial \text{x}}{\partial \overline{\text{w}}} \right\rbrack\]

5.3.4.2.3. EBR-II Pump Model

The third centrifugal pump option in PRIMAR-4 is essentially the pump model used in the NATDEMO code [5-5] for EBR-II. By adjusting the coefficients in the pump characteristics curves, this model could probably also be used for other reactors. This model is somewhat simpler than the option 2 model, in that the EBR-II pump model is mainly applicable to the first quadrant (positive flow, positive pump speed). This model can be used for negative flow, but it is probably not applicable to negative pump speed. Also, for the EBR-II pump model, the user specifies the pump speed as a function of time; whereas in options 1 and 2, the code calculated the pump speed.

In this option, the pump head is calculated from

(5.3-101)\[ \overline{H} = b_{1} {\overline{s}}^{2} + b_{2} \overline{s} \overline{w} + b_{3} \frac{\overline{w}}{\left| \overline{w} \right|} \left| \overline{w} \right|^{b_{4}}\]

where

(5.3-102)\[ \overline{H} = H/H_{\text{r}}\]

(5.3-103)\[ \overline{s} = s/s_{\text{r}}\]

(5.3-104)\[ \overline{w} = w/w_{\text{r}}\]

\(H\) = pump head

\(s\) = pump speed

and

\(w\) = coolant flow rate

The \(r\) subscript refers to the rated value. The coefficients \(b_1\) and \(b_2\) are constant, but the values of \(b_3\) and \(b_4\) depend on the speed and flow rate:

(5.3-105)\[ \begin{align} b_{3} = b_{3\text{m}} && \text{if }\overline{s} > \varepsilon_{\text{m}} \overline{w} \end{align}\]

(5.3-106)\[ \begin{align} b_{3} = b_{3\text{t}} && \text{if }\overline{s} \leq \varepsilon_{\text{m}} \overline{w} \text{ and } w \geq {\overline{w}}_{\text{t}} \end{align}\]

(5.3-107)\[ \begin{align} b_{3} = b_{3\text{l}} && \text{if }\overline{s} \leq \varepsilon_{\text{m}} \overline{w} \text{ and } w < {\overline{w}}_{\text{t}} \end{align}\]

(5.3-108)\[ \begin{align} b_{4} = b_{4\text{t}} && \text{if } \overline{s} > \varepsilon_{\text{m}} \overline{w} \text{ or } w \geq {\overline{w}}_{\text{t}} \end{align}\]

(5.3-109)\[ \begin{align} b_{4} = b_{4\text{l}} && \text{if } \overline{s} > \varepsilon_{\text{m}} \overline{w} \text{ or } w < {\overline{w}}_{\text{t}} \end{align}\]

Eq. (5.3-105) and Eq. (5.3-108) are based on the idea of using a stopped-rotor pressure drop if \(\overline{s} < \varepsilon_{\text{m}} \overline{w}\). Also, the stopped-rotor pressure drop is a laminar value if \(\overline{w} < {\overline{w}}_{\text{t}}\), or a turbulent value if \(\overline{w} \geq {\overline{w}}_{\text{t}}\). The default values for the coefficients are:

(5.3-110)\[ b_{1} = 1.1740\]

(5.3-111)\[ b_{2} = .0818\]

(5.3-112)\[ b_{3\text{m}} = - .2558\]

(5.3-113)\[ b_{3\text{t}} = - .5923\]

(5.3-114)\[ b_{3\text{l}} = - .0471\]

(5.3-115)\[ b_{4\text{t}} = 1.9\]

(5.3-116)\[ b_{4\text{l}} = 1.0\]

(5.3-117)\[ {\overline{w}}_{\text{t}} = .06\]

(5.3-118)\[ \varepsilon_{\text{m}} = .55\]

(5.3-119)\[ H_{\text{r}} = 358,530 ~ \text{(Pa)}\]

(5.3-120)\[ w_{\text{r}} = 250.2 ~ \text{(kg/s)}\]

and

(5.3-121)\[ s_{r} = 14.5 ~ \text{revolutions/s} = 870 ~ \text{rpm}\]

This correlation produces a discontinuity in pump head at the switch from spinning rotor to stopped rotor. With the default values, the pump head is continuous at the transition from turbulent to laminar flow.

For the steady-state initialization in SSPUMP, the initial normalized pump head, \(\overline{H_{0}}\) and flow rate, \(\overline{w_{0}}\) , are known, and Eq. (5.3-101) is solved to find \(\overline{s_{0}}\), the initial steady-state pump speed:

(5.3-122)\[ {\overline{s}}_{\text{o}} = \frac{- b_{2} {\overline{w}}_{0} + \left\lbrack b_{2}^{2} {\overline{w}}_{0}^{2} - 4b_{1} \left( b_{3} {\overline{w}}_{0}^{b_{4}} - {\overline{H}}_{0} \right) \right\rbrack^{1/2}}{2b_{1}}\]

It is assumed that \({\overline{s}}_{0} > \varepsilon_{\text{m}} {\overline{w}}_{0}\), and the values used for \(b_3\) and \(b_4\) in SSPUMP are \(b_{3\text{m}} b_{4\text{t}}\). The user supplies a table of normalized pump speed vs. time, normalized to the initial steady-state speed. The code then interpolates linearly from this table to get pump speeds for the transient calculation.

In PUMPFL where \(\Delta a_0\), \(\Delta a_1\), \(\Delta a_2\), and \(\Delta a_3\) are calculated, \(\Delta a_0\) and \(\Delta a_1\), are calculated using Eq. (5.3-70) and Eq. (5.3-71) or Eq. (5.3-79) and Eq. (5.3-80), as in the other pump options. For this option

(5.3-123)\[ \Delta a_{2} = \Delta t^{2} \frac{\text{dH}}{\text{ds}} \frac{\text{ds}}{\text{dt}} + \Delta a_{2}^{\text{pipe}}\]

with

(5.3-124)\[ \frac{\text{dH}}{\text{ds}} = \frac{\left( 2b_{1}\overline{s} + b_{2}\overline{w} \right) H_{\text{r}}}{S_{\text{r}}}\]

and \(ds/dt\) obtained from the user-specified table of normalized pump speed vs. time:

(5.3-125)\[ \frac{\text{ds}}{\text{dt}} = \frac{s\left( t + \Delta t \right) - s\left( t \right)}{\Delta t}\]

also,

(5.3-126)\[ \Delta a_{3} = \Delta t \frac{\text{dH}}{\text{dw}} + \Delta a_{3}^{\text{pipe}} = \Delta t\ H_{\text{r}} \left\lbrack b_{2} \overline{s} + b_{3} b_{4} \left( \frac{\overline{w}}{\left| w \right|} \right) \left| w \right|^{b_{4} - 1} \right\rbrack + \Delta a_{3}^{\text{pipe}}\]

5.3.4.2.4. Pump Head vs. Flow Option

One pump option in SAS4A/SASSYS‑1 allows the user to specify the normalized pump head as a function only of normalized flow rate. In this option, the normalization is to the initial steady-state values. The user supplies a table of normalized pump head vs. normalized flow rate, and the code uses linear interpolation between the entries in the table.

For this option, \(\Delta a_0\) and \(\Delta a_1\) for the pump are calculated in the same way as for the other pump options. Then

(5.3-127)\[ \Delta a_{2} = 0 + \Delta a_{2}^{\text{pipe}}\]

and

(5.3-128)\[ \Delta a_{3} = \Delta t \frac{\text{dH}}{\text{dW}} + \Delta a_{3}^{\text{pipe}}\]

with \(\text{dH}/\text{dw}\) being evaluated numerically from the table of \(\overline{H}\) vs. \(\overline{w}\):

(5.3-129)\[ \frac{\text{dH}}{\text{dw}} = \frac{H\left( w + .01 w_{0} \right) - H\left( w \right)}{.01 w_{0}}\]

where \(w_0\) is the initial steady state flow rate, \(w\) is the current flow rate, and \(H\) is the pump head.

5.3.4.3. Electromagnetic Pumps

5.3.4.3.1. Electromagnetic Pump

The electromagnetic pump is modeled as a pipe element. The expression for the pump head for the electromagnetic pump is

(5.3-130)\[ \Delta p_{\text{p}} = H_{\text{s}}\left( t \right) \left( 1 - \frac{v_{\text{Na}}}{v_{\text{sy}}} \right)\]

with

(5.3-131)\[ v_{\text{Na}} = \frac{w}{\rho A}\]

where

\(\Delta p_{\text{p}}\) = the pump head

\(H_{\text{s}} \left( t \right)\) = the pump stall head

\(v_{\text{Na}}\) = the sodium velocity at the beginning of the time interval

\(w\) = the pipe flow rate

\(A\) = the pipe area

\(\rho\) = the sodium density

\(v_{\text{sy}}\) = user-supplied synchronous magnetic field velocity

The quantity

(5.3-132)\[ \frac{H_{\text{s}} \left( t \right)}{H_{\text{s}} \left( o \right)}\]

is a user-supplied table of normalized stall head as a function of time.

The contributions to the \(a\)’s in Eqs. 5.2-10 through 5.2-16 for the electromagnetic pump are

(5.3-133)\[ \Delta a_{\text{0}} = \Delta a_{0}^{\text{pipe}}\]

(5.3-134)\[ \Delta a_{1} = \Delta t \Delta p_{\text{p}} \left( t_{3} \right) + \Delta a_{1}^{\text{pipe}}\]

(5.3-135)\[ \Delta a_{2} = \Delta t \left\lbrack H_{\text{s}}\left( t_{4} \right) - H_{\text{s}}\left( t_{3} \right) \right\rbrack \left( 1 - \frac{v_{\text{Na}}}{v_{\text{sy}}} \right) + \Delta a_{2}^{\text{pipe}}\]

(5.3-136)\[ \Delta a_{3} = - \Delta t H_{\text{s}} \left( t_{3} \right) v_{\text{Na}} + \Delta a_{3}^{\text{pipe}}\]

where

\(\Delta p_{\text{p}} \left( t_3 \right)\) = the pump head evaluated at the beginning of the time interval

\(\Delta t\) = the time interval

\(H_{\text{s}} \left( t_3 \right)\) = the stall head at the beginning of the time interval

\(H_{\text{s}} \left( t_4 \right)\) = the stall head at the end of the time interval

5.3.4.3.2. ALMR EM Pumps

In the ALMR design, the primary pumps contain motor-generators that extend the coastdown times of these EM pumps. Since this combination of EM pumps and motor-generators cannot be modeled well with previous SAS4A/SASSYS‑1 pump options, the ALMR program developed a new pump model to handle this configuration. The new model uses a model similar to that used by General Electric in their ARIES-P code. It is based on head and efficiency data obtained by GE and transmitted to ANL (5-29).

In the ALMR design, a synchronous motor is running all of the time during normal operation, but the power to the EM pump does not go through the motor as long as the normal pump power is available. If normal pump power is lost, then the motor becomes a generator, and a switch is thrown automatically to supply voltage from the motor-generator to the pump. The pump coastdown rate is then determined by the inertia of the motor. The motor is designed such that it will initially supply 60% of nominal voltage to the pump. Thus, when normal power is lost and the motor-generator power is switched on there is a sudden drop in pump head and flow followed by a gradual coastdown.

Controlling the Trip Time

There are two options for controlling the time at which the ALMR EM Pump cuts over to the motor-generator. The first method is to set the trip time in input variable APMPHD(7,IPMP) in block PMR4IN. The second method is to set a dynamic trip time using a function. In this case, the Function Block ID is set in input variable ILRPMP. A single argument is passed to the function containing the value of the time at the end of the current PRIMAR-4 time step. If the time exceeds the value returned by the function, then pump cuts-over to the motor generators, and remains in a tripped state for the remainder of the simulation.

Pump Head

The pump head is correlated with an expression of the form

(5.3-137)\[ \overline{H} = \left( \frac{\overline{V}}{\overline{f}} \right)^{3.5}h_{\text{n}}\left( \frac{\overline{w}}{\overline{f}} \right) - L_{\text{f}}{\overline{w}}^{2}\]

where the normalized terms are defined as

(5.3-138)\[ \overline{H} = \frac{H}{H_{\text{r}}}\]

(5.3-139)\[ \overline{V} = \frac{V}{V_{\text{r}}}\]

(5.3-140)\[ \overline{f} = \frac{f}{f_{\text{r}}}\]

(5.3-141)\[ \overline{w} = \frac{w}{w_{\text{r}}}\]

where

\(H\) = pump head

\(H_{\text{r}}\) = rated head

\(V\) = pump voltage

\(V_{\text{r}}\) = rated voltage

\(f\) = frequency

\(f_{\text{r}}\) = rated frequency

\(w\) = mass flow rate

\(w_{\text{r}}\) = rated mass flow rate

\(L_{\text{f}}\) = friction loss coefficient

and \(h_{\text{n}}\) is a head curve correlated as

(5.3-142)\[ h_{\text{n}}\left( \frac{\overline{w}}{\overline{f}} \right) = \sum_{\text{j} = 1}^{5}{a_{\text{j}}\left( \frac{\overline{w}}{\overline{f}} \right)^{j - 1}}\]

with the coefficients \(a_{\text{j}}\) determined by a least-squares fit to the data.

Pump Efficiency

The pump efficiency, \(\varepsilon_{\text{f}}\), is correlated as

(5.3-143)\[ \varepsilon_{\text{f}} = F \left( \overline{V} \right) G \left( \frac{\overline{w}}{\overline{f}} \right) \varepsilon_{\text{fr}}\]

with

(5.3-144)\[ F \left( \overline{V} \right) = \sum_{\text{j} = 1}^{7}{b_{\text{j}}{\overline{V}}^{j - 1}}\]

(5.3-145)\[\begin{split} G \left( \frac{\overline{w}}{\overline{f}} \right) = \begin{cases} 0.01 & \text{if }\frac{\overline{w}}{\overline{f}} \geq 5 \\ \sum_{\text{j} = 1}^{9}{c_{\text{j}} \left( \frac{\overline{w}}{\overline{f}} \right)^{j - 1}} & \text{if }\frac{\overline{w}}{\overline{f}} \leq 5 \\ \end{cases}\end{split}\]

and \(\varepsilon_{\text{fr}}\) is the rated efficiency

Pump Voltage

Before the cut-over to the motor-generator, the pump voltage is assumed to be constant at its rated value. Also, the frequency is constant at its rated value. Immediately after cut-over, the voltage drops to a fraction, \(V_{\text{fr}}\), of its initial value. Then the voltage is proportional to the square of the frequency, so after cut-over the voltage is

(5.3-146)\[ \overline{V} = V_{\text{fr}}{\overline{f}}^{2}\]

Motor Speed

The equation for the motor speed, \(s\), is

(5.3-147)\[ \frac{\text{ds}}{\text{dt}} = - \frac{\tau_{\text{p}} + \tau_{\text{l}}}{I}\]

where

\(\tau_{\text{p}}\) = pump torque

\(\tau_{\text{l}}\) = friction loss

\(I\) = moment of inertia

Note that the motor speed and the pump frequency are the same:

(5.3-148)\[ f = s\]

The pump torque is given by

(5.3-149)\[ \tau_{\text{p}} = \frac{Hw}{\varepsilon_{\text{f}} \rho s}\]

where

\(\rho\) = liquid density

The friction loss in the motor is assumed to have the form

(5.3-150)\[ \tau_{\text{l}} = \tau_{\text{r}} L_{\text{m}} s\]

where \(L_{\text{m}}\) is a loss coefficient and \(\tau_{\text{r}}\), the rated torque, is given by Eq. (5.3-149) with rated values used for all terms.

Correlations to Pump Data

Reference 5-29 transmitted the data taken for the pump. This data has been fit by a least-squares fitting program to give the parameters listed in Table 5.3.5 for use in Eq. (5.3-142), Eq. (5.3-144), and Eq. (5.3-145). Also a value of .07592 is used for \(L_{\text{f}}\) in Eq. (5.3-137). Table 5.3.6 lists the data from Ref. 5-29, as well as the head and efficiency values calculated using the correlations of equations Eq. (5.3-137), Eq. (5.3-142), Eq. (5.3-143), and Eq. (5.3-145) with the coefficients in Table 5.3.5. Also, some of this data is plotted in Figure 5.3.1 and Figure 5.3.2. It can be seen that the correlations match the data well except for a couple of points.

Table 5.3.5 Correlation Coefficients for Use with the ALMR EM Pump Model

\(j\)	\(a_{\text{j}}\)	\(b_{\text{j}}\)	\(c_{\text{j}}\)
1	1.133	-.148
2	.996	7.110	-51.235
3	-2.498	-15.972	684.934
4	6.056	9.942	-3483.628
5	-4.611	12.024	9119.690
6		-18.536	-13449.761
7		6.577	11279.948
8			-5014.503
9			915.555

Table 5.3.6 Pump Head and Efficiency for the ALMR EM Pump Model

Normalized Voltage	Normalized Frequency	Normalized Flow	Measured Normalized Head	Fit Normalized Head	Measured Efficiency	Fit Efficiency
1.000	1.000	1.148	0.042	0.041	0.115	0.133
1.000	1.000	1.124	0.250	0.242	0.505	0.469
1.000	1.000	1.086	0.500	0.524	0.781	0.807
1.000	1.000	1.000	1.000	1.000	1.000	0.997
1.000	1.000	0.800	1.483	1.494	0.928	0.915
1.000	1.000	0.600	1.508	1.514	0.710	0.709
1.000	1.000	0.400	1.399	1.389	0.469	0.468
1.000	1.000	0.200	1.265	1.270	0.229	0.229
1.000	1.000	0.0	1.134	1.133	0.0	0.0
0.627	0.778	0.886	0.042	0.042	0.183	0.256
0.627	0.778	0.862	0.167	0.158	0.551	0.600
0.627	0.778	0.824	0.333	0.314	0.817	0.879
0.627	0.778	0.762	0.581	0.500	0.970	0.932
0.628	0.778	0.762	0.581	0.505	0.970	0.932
0.312	0.472	0.532	0.042	0.052	0.318	0.381
0.312	0.472	0.520	0.083	0.097	0.529	0.608
0.312	0.472	0.495	0.167	0.178	0.773	0.848
0.312	0.472	0.476	0.227	0.226	0.863	0.884
1.202	1.111	1.143	1.306	1.144	1.008	1.009
0.929	0.944	0.952	0.905	0.912	0.998	1.003
0.820	0.833	0.857	0.734	0.835	0.986	0.981
0.519	0.667	0.667	0.444	0.415	0.954	0.932
0.437	0.556	0.571	0.327	0.383	0.917	0.920
0.251	0.500	0.476	0.227	0.096	0.855	0.789
0.219	0.389	0.381	0.145	0.143	0.757	0.757
0.153	0.278	0.286	0.082	0.111	0.567	0.602
0.071	0.222	0.190	0.037	0.025	0.268	0.255
0.027	0.111	0.095	0.009	0.010	0.026	0.031

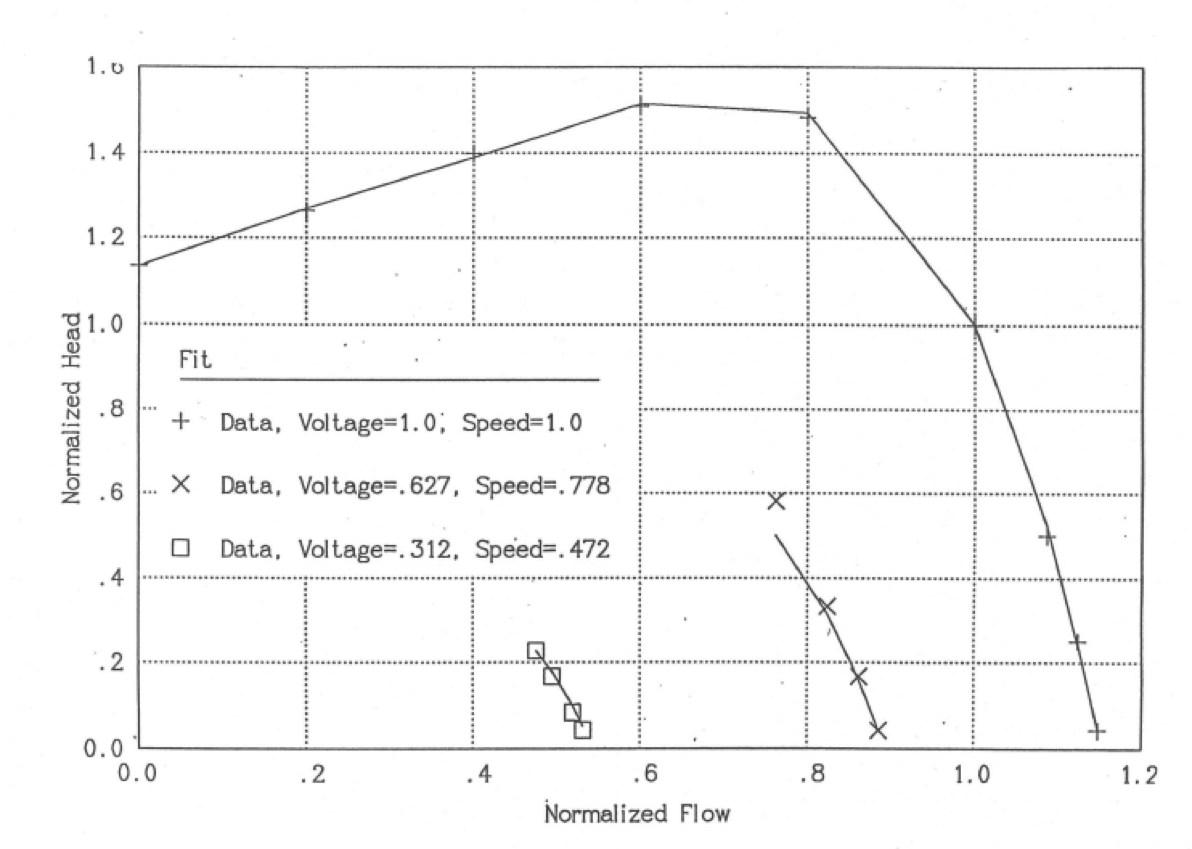
Figure 5.3.1 Pump Head, Data and Fits for the ALMR EM Pump Model.

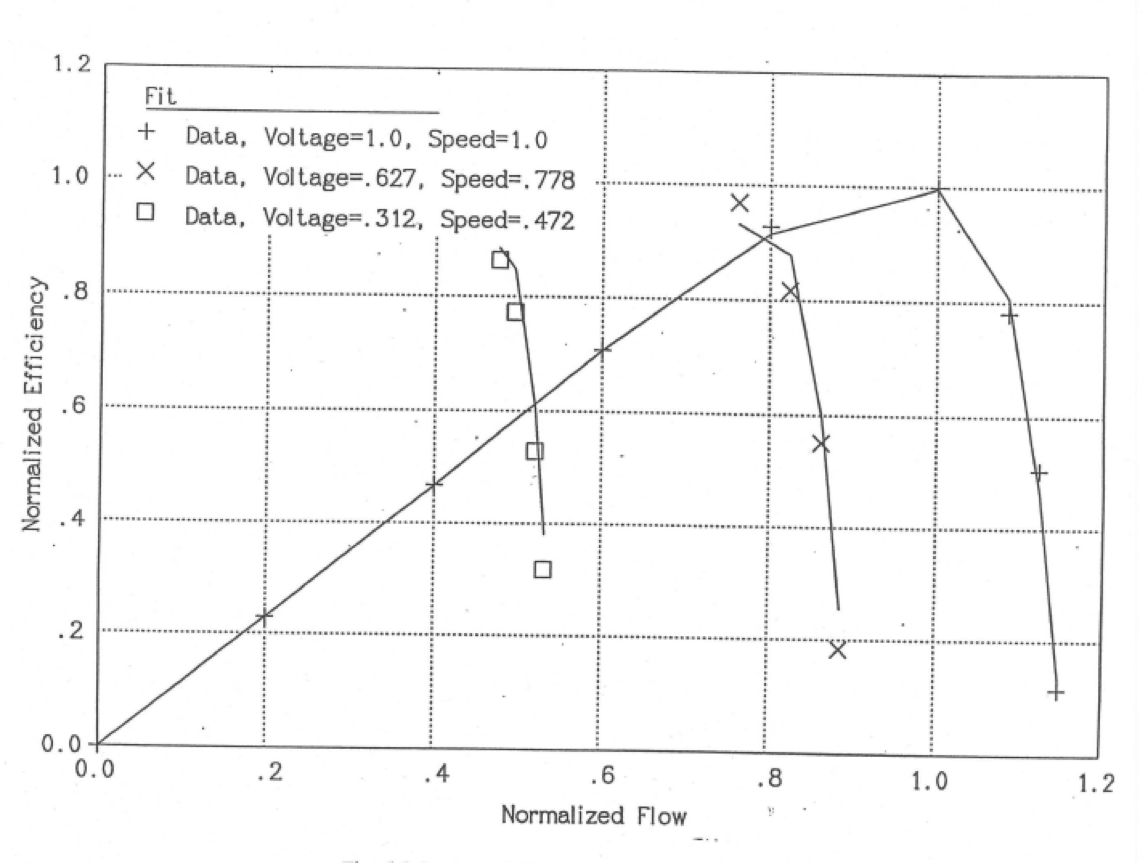
Figure 5.3.2 Pump Efficiency, Data and Fits for the ALMR EM Pump Model.

5.3.4.3.3. Equivalent Circuit EM Pump

Equivalent circuit theory enables generalized systems-level modeling of EM pumps based on an electric circuit with components that represent the main responses of the pump. By representing the various dissipative and inertial aspects of the pump with resistors and inductors within a hypothetical electrical circuit, traditional circuit analysis techniques are used to approximate the pump’s internal energy flow. Benefits of equivalent circuit theory within SAS include generic pump control as functions of voltage and frequency, flexibility to model a range of pump designs and operating conditions, and computational efficiency.

Two pump models are available on the basis of equivalent circuit theory, referred to as the “detailed” and “simple” models. With the exception of the governing circuit and consequent governing equations, the two models share the same framework, features, and calculation procedures. The common features are discussed here, while the details that differ between the two models are discussed in the subsections below and Section 5.16.7.

The equivalent circuit models assume that the pump is a three-phase, wye-connected, linear electromagnetic pump (annular or non-annular, depending on the specification of ITYPEL). Assuming each phase is equally loaded, all phases are represented using a single circuit of either detailed or simple type. Equating the circuit prediction for electrical power dissipation in resistors representing fluid mechanical power with the hydraulic power imparted to the fluid, the pressure developed by the pump (not including friction, gravity, or form losses) is predicted as

(5.3-151)\[ \Delta p_P = \frac{3 I^2 \Psi(s)}{Q}\]

where

\(\Delta p_P\) = pump developed pressure

\(I\) = total phase current

\(Q\) = fluid volumetric flowrate

\(\Psi(s)\) = model-dependent circuit transform function

\(s\) = \(1 - \frac{v_f}{v_s}\) = slip

\(v_f\) = fluid velocity

\(v_s\) = pump synchronous speed

Due to the limited inertia of EM pumps, a quasi-static assumption is employed in solving for \(I\) and \(\Psi\). Therefore the steady-state circuit equations are solved at each transient time step.

Based on this expression, the contributions to the \(\Delta a_i(k)\)’s in Equations 5.2-10, 5.2-12, 5.2-14, and 5.2-16 are:

(5.3-152)\[ \Delta a_0(k) = \Delta a_{0}^{\text{pipe}}\]

(5.3-153)\[ \Delta a_1(k) = \Delta t \Delta p_P(k) + \Delta a_{1}^{\text{pipe}}\]

(5.3-154)\[ \Delta a_2(k) = \Delta a_{2}^{\text{pipe}}\]

(5.3-155)\[ \Delta a_3(k) = \Delta t \frac{\partial \Delta p_P(k)}{\partial w} + \Delta a_{3}^{\text{pipe}} \approx \Delta t \frac{\Delta p_P(k,1.01(w+10^{-6}))- \Delta p_P(k,w)}{0.01 w + 1.01*10^{-6}} + \Delta a_{3}^{\text{pipe}}\]

Pump efficiency is calculated by dividing fluid power in the forward direction by the electrical power dissipated in the entire pump (including all three phases) as

(5.3-156)\[\eta = \frac{\left(\Delta p_P - \Delta p_f\right) \cdot Q}{3 V_s I \cos{\phi}}\]

where

\(\eta\) = efficiency

\(\Delta p_f\) = friction losses in the pump element

\(V_s\) = power source phase voltage

\(\phi\) = phase angle

Arbitrary control of the pump’s power supply is enabled through the use of FUNCTION blocks to individually control voltage and frequency with time.

The steady-state initialization process is outlined in Figure 5.3.3.

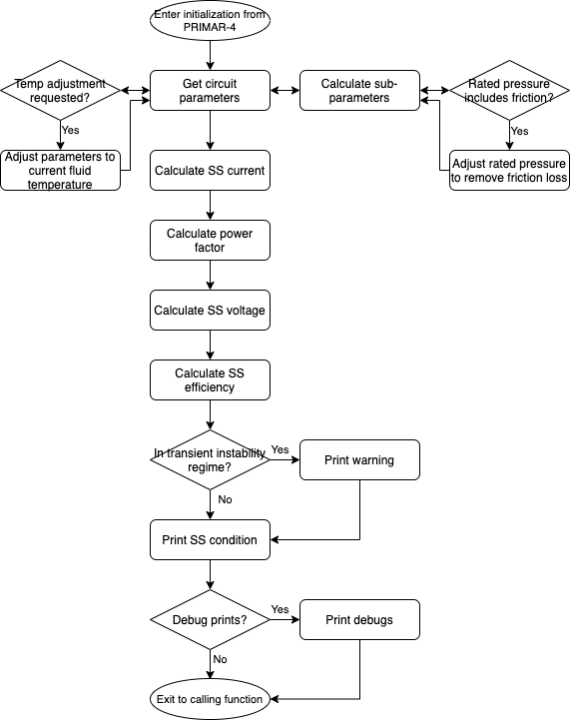
Figure 5.3.3 Flow chart of the steady-state initialization procedure for equivalent circuit pumps.

The resistance representing Joule heating is adjusted for fluid temperature using TR. In the case that TR is specified, the Joule resistance is assumed to be proportional to the temperature-dependent fluid electrical resistance as discussed specifically for each model. The default correlation for sodium electrical resistivity is given in Eq. (5.3-157), with \(371 \text{ K} \leq T \leq 1373 \text{ K}\) [5-10].

(5.3-157)\[\rho_r(T) = C_1 + C_2 T + C_3 T^2\]

where

\(C_1\) = 7.756E-8 Ω-m

\(C_2\) = 2.054E-10 Ω-m/C

\(C_3\) = 3.481E-13 Ω-m/C^2

\(T\) = fluid temperature

The user may also enter their own correlation coefficients to be used in Eq. (5.3-157) as described in Table 5.3.8 for either sodium or when other coolants are employed (see ICLPRP and INAS3D).

Once circuit parameters are deduced, initialization uses the flow rate and pressure across the pump element as determined by PRIMAR-4 to determine the pump’s current, power factor, voltage, and efficiency at steady-state. The steady-state pump voltage is then stored as the amplitude of the normalized voltage used during transient steps.

Pump heating may be modeled for equivalent circuit pumps using the scaling factor fH. This feature is discussed within the temperature calculation section.

5.3.4.3.3.1. Detailed Circuit Model

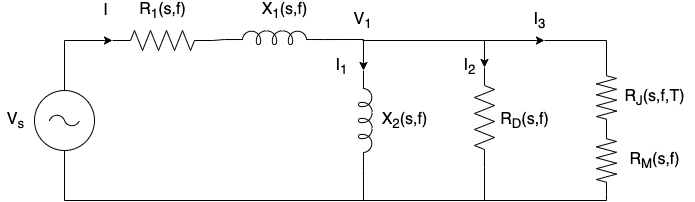
Figure 5.3.4 Equivalent circuit of one phase of an annular linear induction pump used in the detailed circuit model.

The equivalent circuit used in the detailed model is shown in Figure 5.3.4 where

\(R_1\) = primary electrical resistance

\(R_D\) = electrical resistance of ducts

\(R_J\) = Joule heating resistance

\(R_M\) = fluid mechanical work resistance

\(X_1\) = \(2 \pi f L_1\) = coil leakage reactance

\(X_2\) = \(2 \pi f L_2\) = magnetizing reactance

\(L_1\) = coil leakage inductance

\(L_2\) = magnetizing inductance

\(f\) = power source frequency

Note that all circuit parameters in the detailed circuit model can be functions of both \(s\) and \(f\). These functionalities are specified using FUNCTION blocks.

Using this circuit, \(\Psi\) in Eq. (5.3-151) is

(5.3-158)\[\Psi= \frac{R_m R_D^2 X_2^2}{(R_j+R_m)^2 R_D^2 +(R_J+R_m+R_D)^2X_2^2}\]

Steady-state initialization of the detailed circuit model starts by evaluating the initial frequency specified through fFuncID. Using this, the initial slip is calculated with the user-provided synchronous speed. Having both frequency and slip, the respective FUNCTION blocks for each of the circuit parameters are evaluated at \(t\) = 0.

If temperature adjustment of circuit parameters is requested, \(R_J\) at each timestep is adjusted to \(R_J'\) using the proportionality relation

(5.3-159)\[R_J' = C \rho_r(T)\]

where \(C\) is a proportionality constant determined using the value of \(R_J\) at \(t\) = 0 along with TR.

5.3.4.3.3.2. Simple Circuit Model

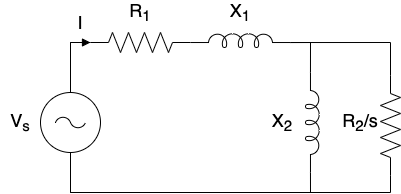
Figure 5.3.5 Equivalent circuit of one phase of an annular linear induction pump used in the simple circuit model.

The equivalent circuit used in the simple model is shown in Figure 5.3.5 where \(R_2\) is a resistance representing both Joule and mechanical power. Note that all circuit parameters in the simple circuit model are assumed constant.

Using this circuit, \(\Psi\) in Eq. (5.3-151) is

(5.3-160)\[\Psi = \frac{R_2(1-s)}{s \left( \frac{R_2^2}{X_2^2 s^2} + 1 \right)}\]

Determination of circuit parameters during steady-state initialization of the simple circuit model consists of an inversion process using “rated” conditions specified by the user. In this way, the user is not required to know specific electrical/geometric details of the pump, but rather specifies only operating characteristics instead, making the simple model easier to use when pump details are unknown. In this case, “rated” conditions can be any operating state of the pump, though all specified rated conditions for a given pump should be for a fixed operation point (i.e. it is not permissible to specify rated flow at one voltage and rated current at another).

The equations used for determining the circuit parameters are

(5.3-161)\[R_2 = \frac{\Delta P_{P,R}(A_Rv_s\frac{s_R^2-1}{s_R})}{3I_R^2-3I_S^2\frac{\Delta P_{P,R}}{\Delta P_S s_R}}\]

(5.3-162)\[X_{2,R} = \frac{R_2}{\sqrt{\frac{3 I_S^2 R_2}{A_R v_{s,R} \Delta P_{P,S} } - 1}}\]

(5.3-163)\[R_1 = \frac{\frac{\Delta P_{P,R} Q_R}{3I_R^2 \eta_R}(R_2^2+X_2^2s_R^2) - s_R R_2 X_2^2}{R_2^2+X_2^2s_R^2}\]

(5.3-164)\[X_{1,R} = \left[\left(\frac{V_R}{I_R}\right)^2 -\left(R_1 + \frac{s_R R_2 X_2^2}{R_2^2+s_R^2 X_2^2}\right)^2 \right]^{0.5} - \frac{R_2^2X_2}{R_2^2 + X_2^2s_R^2}\]

where the subscripts \(R\) and \(S\) indicate rated and stall (i.e. zero flow) conditions, respectfully.

iDPOPT is used to adjust \(\Delta p_R\) for friction losses if requested by the user. Then all values in Eq. (5.3-161) - Eq. (5.3-164) can be deduced from user input except for \(I_S\). Therefore these equations are solved using a fixed-point iteration on \(I_S\) until convergence to within epsIs is achieved. Once converged, \(L_1\) and \(L_2\) are deduced using \(f_R\). Steady-state circuit reactances are then calculated using frequency at \(t\) = 0 specified through f0. Note that the inversion process used to arrive at Eq. (5.3-161) - Eq. (5.3-164) makes the determinination of circuit parameters in the simple circuit model highly sensitive to the rated conditions specified. For this reason, a set of suggested values to represent a realistic pump are provided Table 5.3.10.

If temperature adjustment of circuit parameters is requested, \(R_2\) at each timestep is adjusted to \(R_2'\) using the proportionality relation

(5.3-165)\[R_2' = C \rho_r(T)\]

where \(C\) is determined as outlined for the detailed circuit model.

5.3.4.3.3.3. Model Inputs

Inputs for equivalent circuit models consist of data entered in both EMPUMP blocks and in standard input records. In addition to those inputs required for all liquid elements in INPMR4 and PMR4IN, standard input records related specifically to equivalent circuit pumps are highlighted in Table 5.3.7.

Table 5.3.7 INPMR4 inputs for Equivalent Circuit models.

Variable	Description
ITYPEL(IELL)	Liquid element type of element IELL, specify 5 for a non-annular pump or 15 for an annular .
IELPMP(IPMP)	Element number corresponding to pump IPMP.
IEMPMP(IPMP)	Option to specify that pump IPMP uses the equivalent circuit EM pump model (IEMPMP = -3).
ILRPMP(IPMP)	EMPUMP block number containing information for equivalent circuit pump IPMP.

For pumps specified as annular (ITYPEL = 15), a number of additional inputs are required in INPMR4 and PMR4IN.

The required EMPUMP block inputs are highlighted below by those which are common to all models, those which are specific to the detailed circuit model, and those which are specific to the simple circuit model. For the simple circuit model, suggested values are provided to represent the pump from Ref. [5-11].

Table 5.3.8 EMPUMP block inputs common to all Equivalent Circuit model options.

Keyword	Description	Units	Type	Range
VFuncID	FUNCTION block number corresponding to \(V_s(t)\), the normalized pump voltage with time. If omitted, voltage is held constant at steady-state value. If \(V_s(0)\) ≠ 1, table will be normalized to the steady-state value.	–	Integer, optional	0 < VFuncID
fFuncID	FUNCTION block number corresponding to \(f(t)\), the normalized pump frequency with time.	–	Integer	0 < fFuncID
f0	Initial frequency of the pump.	Hz	Float	0 < f0
fH	Fraction of pump heating to be included in thermal calculations. If omitted, pump heating is turned off.	–	Float, optional	0 ≤ fH
fOD	Fraction of pump heating to be deposited in outer wall of an annular pump element. Ignored for pipe-type pumps. If omitted, \(F_{OD}=\frac{MC_{OD}}{MC_{OD}+MC_{ID}}\), where \(MC_{OD}\) is WALLMC and \(MC_{ID}\) is WALMC2.	–	Float, optional	0 ≤ fOD ≤ 1
TR	Temperature of fluid flow through the pump at rated conditions. If omitted, temperature dependence of circuit parameters is turned off.	K	Float, optional	0 ≤ TR
C1	Constant coefficient in Eq. (5.3-157). If any of C1, C2, or C3 are provided, all three defaults are overwritten.	Ω-m	Float, optional	–
C2	Linear coefficient in Eq. (5.3-157). If any of C1, C2, or C3 are provided, all three defaults are overwritten.	Ω-m/C	Float, optional	–
C3	Quadratic coefficient in Eq. (5.3-157). If any of C1, C2, or C3 are provided, all three defaults are overwritten.	Ω-m/C^2	Float, optional	–

Table 5.3.9 Model inputs for the DETAILED option.

Keyword	Description	Units	Type	Range
R1FuncID	FUNCTION block number corresponding to 𝑅1(𝑠,𝑓).	–	Integer	0 < R1FuncID
RDFuncID	FUNCTION block number corresponding to 𝑅D(𝑠,𝑓).	–	Integer	0 < RDFuncID
RJFuncID	FUNCTION block number corresponding to 𝑅J(𝑠,𝑓).	–	Integer	0 < RJFuncID
RMFuncID	FUNCTION block number corresponding to 𝑅M(𝑠,𝑓).	–	Integer	0 < RMFuncID
L1FuncID	FUNCTION block number corresponding to 𝐿1(𝑠,𝑓).	–	Integer	0 < L1FuncID
L2FuncID	FUNCTION block number corresponding to 𝐿2(𝑠,𝑓).	–	Integer	0 < L2FuncID
vs	Synchronous pump speed corresponding to \(f(0)\).	m/s	Float	0 < vs

Table 5.3.10 Model inputs for the SIMPLE option.

Keyword	Description	Units	Type	Range	Suggested Value
dPR	Developed pressure over the pump at rated conditions.	Pa	Float	0 < dPR	2.0E5
dPS	Developed pressure over the pump at stall conditions (i.e. zero flow) at rated voltage and frequency.	Pa	Float	0 < dPS	3.0E5
etaR	Fractional pump efficiency at rated conditions.	–	Float	0 < etaR ≤ 1	0.45
IR	Phase current at rated conditions.	A	Float	0 < IR	1700
VR	Phase voltage at rated conditions.	V	Float	0 < VR	510
fR	Power supply frequency at rated conditions.	1/s	Float	0 < fR	12
WR	Mass flow rate through the pump at rated conditions.	kg/s	Float	0 < WR	1333
sR	Slip at rated conditions.	–	Float	0 < sR < 1	0.2
iDPOPT	If iDPOPT ≠ 0, rated and stall input parameters have been adjusted to account for pressure losses. If iDPOPT = 0 or omitted, rated and stall input parameters are based on net pressure rise.	–	Integer, optional	–	1
espIs	Fractional convergence tolerance of the fixed-point iteration to determine stall current. If omitted, epsIS = 10E-8.	–	Float, optional	0 < epsIs	–

Example input showing a detailed-circuit annular pump along with a simple-circuit non-annular pump:

INPMR4     3     1     0
#
# NELEMT
    10 : 2       # only two elements
# ITYPEL
    49 : 5 15    # first is a pump, second is annular pump
# NANEL
  1243 : 1       # one element is annular
# IELANE
  1244 : 2       # element 2 is the annular element
# NPUMP
   405 : 2       # two pumps
# IELPMP
   406 : 1 2     # elements 1 and 2 are pumps
# IEMPMP
   418 : -3 -3   # pumps 1 and 2 are equivalent circuit pumps
# ILRPMP
   430 : 1 2     # eq circ pumps correspond to EMPUMP blocks 1 and 2, respectively
#
# other integer inputs, including segments, CVs, temperature groups, etc...
#
    -1
#
PMR4IN    18     1     0
#
# element float inputs, including ZOUTEL, XLENEL, AREAEL, etc...
#
# annular element float inputs, including WALMC2,  WALLH2, etc...
#
    -1
#
EMPUMP 1 SIMPLE
    VFuncID = 1
    fFuncID = 1
    f0 = 12
    fH = 0.5          # pump heat is modeled at half strength
    TR = 0            # do not adjust R2 for temperature
    dPR = 0.2E6
    dPS = 0.3E6
    etaR = 0.45
    IR = 1700.
    VR = 850.
    fR = 12.
    WR = 1333
    sR = 0.2
    epsIs = 1E-10
    iDPOPT = 1

    FUNCTION 1 "VoltageAndFrequencyFunction"
        TYPE = TABLE
        SOURCE = 1
    END

    # voltage and frequency hold constant
    TABLE 1 VoltageTable
        x    y
        0    1
        1    1
    END
END

EMPUMP 2 DETAILED
    fFuncID = 1
    VFuncID = 10
    f0 = 12
        fOD = 0.5
    fH = 0       # pump heat is not modeled
    TR = 573.15  # adjust RJ for temperature, using 573.15 K to determine proportionality constant
    vs = 12.
    R1FuncID = 2
    RDFuncID = 3
    RJFuncID = 4
    RMFuncID = 5
    L1FuncID = 6
    L2FuncID = 7

    # voltage is halved after 100 seconds
    FUNCTION 10 "VoltageFunction"
        TYPE = TABLE
        TABLE 1 VoltageTable
            x    y
            0    1
            100  0.5
        END
    END

    # frequency doubles after 100 seconds
    FUNCTION 1 "FrequencyFunction"
        TYPE = TABLE
        TABLE 1 FrequencyTable
            x    y
            0      1
            100    2
        END
    END

    # R1 holds constant
    FUNCTION 2 "R1Function"
        TYPE = TABLE
        TABLE 1 SuperLocalTable
            x    y
            0    0.08
            1    0.08
        END
    END

    # RD holds constant
    FUNCTION 3 "RDFunction"
        TYPE = TABLE
        TABLE 1 RDTable
            x    y
            0    10.
            1    10.
        END
    END

    # RD holds constant
    FUNCTION 4 "RJFunction2"
        TYPE = TABLE
        TABLE 1 RJTable
            x    y
            0    0.44
            1    0.44
        END
    END

    # RM holds constant
    FUNCTION 5 "RMFunction"
        TYPE = TABLE
        TABLE 1 RMTable
            x    y
            0    0.7
            1    0.7
        END
    END

    # L1 holds constant
    FUNCTION 6 "L1Function"
        TYPE = TABLE
        TABLE 1 L1Table
            x    y
            0    0.004
            1    0.004
        END
    END

    # L2 holds constant
    FUNCTION 7 "L2Function"
        TYPE = TABLE
        TABLE 1 L2Table
            x    y
            0    0.01
            1    0.01
        END
    END
END