5.6. Air Dump Heat Exchanger

SAS4A/SASSYS‑1 contains a simple quasi-static sodium-to-air heat exchanger model. This model is intended mainly for use with a DRACS (Direct Reactor Auxiliary Cooling System), as shown in Figure 5.6.1; but it could also be used as a main heat rejection component, such as for the air dump heat exchangers on the FFTF reactor.

The model can handle either forced convection or natural circulation air flow. For a forced convection case, the user supplies the air flow as a function of time. For a natural circulation case, the user supplies a table of the stack inlet loss coefficient vs. time. The stack inlet loss coefficient represents the shutter opening, which may change during the transient.

A log mean temperature model is used for both the sodium side and the air side of the heat exchanger. Heat capacity of the tube structural material is ignored.

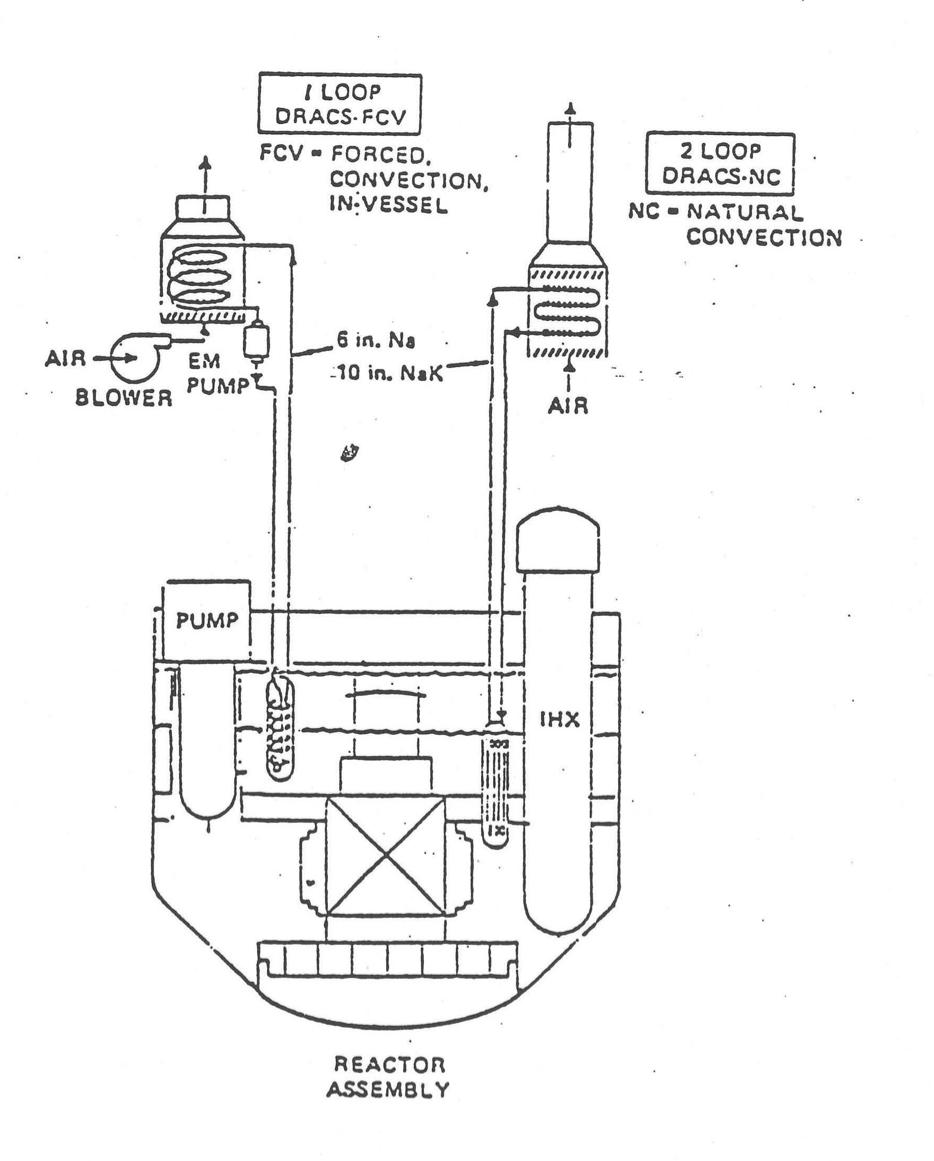
Figure 5.6.1 Shutdown Heat Removal System for a Large Pool Plant.

5.6.1. Methodology

Equations used in the model are as follow: For the coolant, we ignore storage of energy within the heat exchanger and assume specific heat is independent of temperature so that an energy balance gives

(5.6-1)\[ Q = w_{\text{Na}} C_{\text{Na}} \left( T_{\text{Nat}} - T_{\text{Nab}} \right) = w_{\text{a}} C_{\text{a}} \left( T_{\text{at}} - T_{\text{ab}} \right)~,\]

where

\(Q\) = heat removal rate,

\(w\) = mass flowrate,

\(C\) = specific heat,

\(T\) = temperature,

\(a\) = air side subscript,

\(Na\) = liquid metal side subscript,

\(t\) = subscript for the top of the heat exchanger,

\(b\) = subscript for the bottom of the heat exchanger.

The momentum equation for the air side is from Section 5.16.4

(5.6-2)\[ w^{2} = \frac{\left( \rho_{\text{c}} - \rho_{\text{h}} \right) g\mathcal{l}A_{\text{R}}^{2}}{\frac{K_{\text{SI}}}{2\rho_{\text{c}}} \left( \frac{A_{\text{g}}}{A_{\text{SI}}} \right)^{2} + \frac{K_{\text{HX}}}{2\rho_{\text{c}}} \left( \frac{A_{\text{g}}}{A_{\text{HX}}} \right)^{2} + \frac{K_{\text{SO}} + K_{\text{R}}}{2\rho_{\text{h}}} }\]

where

\(w\) = air mass flowrate,

\(A\) = area,

\(\rho_{\text{c}}\) = inlet air density,

\(\rho_{\text{h}}\) = outlet air density,

\(K\) = loss coefficient,

\(\text{l}\) = height of stack,

\(\text{SI}\) = stack inlet subscript,

\(\text{SO}\) = stack outlet subscript,

\(R\) = riser subscript

\(g\) = acceleration of gravity.

The overall heat transfer coefficient evaluated at the tube outside surface (air side) is

(5.6-3)\[ U = \left\lbrack \frac{r_{\text{o}}}{r_{\text{i}}h_{\text{i}}} + \frac{r_{\text{o}}}{k} \ln{\frac{r_{\text{o}}}{r_{\text{i}}}} + \frac{1}{h_{\text{o}}} \right\rbrack^{-1}~ ,\]

where

\(h_{\text{i}}\) = tube inside heat transfer coefficient,

\(h_{\text{o}}\) = tube outside heat transfer coefficient,

\(r_{\text{i}}\) = tube inner radius,

\(r_{\text{o}}\) = tube outer radius,

\(k\) = thermal conductivity.

In this implementation of the model, the heat transfer coefficients \(h_{\text{i}}\) and \(h_{\text{o}}\) are treated as constants and are input by the user. Strictly, however, their values change with fluid temperature and flowrate. Typically, \(h_{\text{o}}\) dominates Eq. (5.6-3) and because the air side is a complex geometry of pins and tubes, its value is not accurately known. Therefore, assuming a constant value for \(h_{\text{o}}\) that is credible should not introduce appreciably more error than the uncertainty that already exists because of its complex geometry.

The basic equations for temperatures are

(5.6-4)\[ W_{\text{Na}} C_{\text{Na}} \frac{dT_{\text{Na}}}{\text{dz}} + \frac{\text{UA}}{L} \left( T_{\text{a}} - T_{\text{Na}} \right) = 0\]

and

(5.6-5)\[ - W_{\text{a}} C_{\text{a}} \frac{\text{dT}_{\text{a}}}{\text{dz}} + \frac{\text{UA}}{L} \left( T_{\text{Na}} - T_{\text{a}} \right) = 0\]

where

\(T_{\text{Na}}\) = sodium temperature

\(T_{\text{a}}\) = air temperature

\(z\) = elevation

\(W_{\text{Na}}\) = sodium flow rate

\(W_{\text{a}}\) = air flow rate

\(C_{\text{Na}}\) = sodium heat capacity

\(C_{\text{a}}\) = air heat capacity

\(U\) = heat transfer coefficient

\(A\) = total heat transfer area, and

\(L\) = height of the heat transfer section

The solution of Eq. (5.6-4) and Eq. (5.6-5) of the form

(5.6-6)\[ T_{\text{Na}} = T_{\text{a}} = ae^{\alpha z}\]

where \(a\) is a constant, and

(5.6-7)\[ \alpha = \frac{\left( W_{\text{a}}C_{\text{a}} + W_{\text{Na}} C_{\text{Na}} \right) \text{UA}/L}{W_{\text{a}}C_{\text{a}}W_{\text{Na}} C_{\text{Na}}}\]

\(T_{\text{Nab}}\) = sodium outlet temperature, and

\(T_{\text{ab}}\) = air inlet temperature

The sodium temperature then has the form

(5.6-8)\[ T_{\text{Na}} = b + ce^{\alpha z}\]

The gravity head is

(5.6-9)\[ \Delta p_{\text{gr}} = \int_{0}^{L}{\rho_{\text{Na}} \left( z \right)} \text{dz}\]

where \(\rho_{\text{Na}}\) is the sodium density and \(z = 0\) at the bottom of the heat transfer section. The thermal center, \(z_{\text{tc}}\), is defined by

(5.6-10)\[ \Delta p_{\text{gr}} = \rho_{\text{Nat}} \left( L - z_{\text{tc}} \right) + \rho_{\text{Nab}} z_{\text{tc}}\]

where

\(\rho_{\text{Nat}}\) = sodium density at the top and

\(\rho_{\text{Nab}}\) = sodium density at the bottom

If the density varies linearly with temperature, then an equivalent equation for the thermal center is

(5.6-11)\[ T_{\text{Nat}} \left( L - z_{\text{tc}} \right) + T_{\text{Nab}} Z_{\text{tc}} = \int_{0}^{L}{T_{\text{Na}}\left( z \right)} \text{dz}\]

where \(T_{\text{Nat}}\) is the sodium temperature at the top of the heat transfer section. Carrying out the integration of Eq. (5.6-8) in Eq. (5.6-11) gives

(5.6-12)\[ z_{\text{tc}} = L \left\lbrack \frac{1}{\left( 1 - e^{- \alpha L} \right)} - \frac{1}{\alpha L} \right\rbrack\]

For the steady-state initialization, conservation of energy gives

(5.6-13)\[ W_{\text{Na}} C_{\text{Na}} \left( T_{\text{Nat}} - T_{\text{Nab}} \right) = W_{\text{a}} C_{\text{a}} \left( T_{\text{at}} - T_{\text{ab}} \right)\]

Also, Eq. (5.6-6) can give

(5.6-14)\[ \frac{T_{\text{Nat}} - T_{\text{at}}}{T_{\text{Nab}} - T_{\text{ab}}} = x = e\]

combining Eq. (5.6-13) and Eq. (5.6-14) gives

(5.6-15)\[ T_{\text{Nab}} = \frac{xW_{\text{a}} C_{\text{a}}}{xW_{\text{a}} C_{\text{a}} - W_{\text{Na}} C_{\text{Na}}} \left\lbrack T_{\text{ab}} \left( 1 - \frac{1}{x} \right) + \frac{T_{\text{Nat}}}{x} \left( 1 - \frac{W_{\text{Na}} C_{\text{Na}}}{W_{\text{a}} C_{\text{a}}} \right) \right\rbrack\]

The above equations are solved by subroutine NAKAIR. SAS4A/SASSYS‑1 couples to this routine as follows: Values for liquid metal flowrate at the heat exchanger inlet, the temperature at this point and the inlet air temperature are passed as computed by SAS4A/SASSYS‑1 to subroutine NAKAIR. This routine solves the above equations for the temperature drop on the liquid metal side of the heat exchanger and returns this value to SAS4A/SASSYS‑1 which uses it to advance to the next time step.

The subroutine is also applicable to the case where the air flowrate is forced. In this case, the known air mass flowrate is used in place of Eq. (5.6-2).

5.6.2. Steady-State Solution

A capability has been added to the SAS4A/SASSYS‑1 air dump heat exchanger (DHX) model to provide a steady-state initialization procedure that will calculate the air flow rate required to remove the steady-state power delivered to the heat exchanger. What is done with the steady-state air flow rate in the DHX depends on whether the forced air flow option or the natural circulation air flow option is used. For forced flow, the user-supplied table of air-flow rate vs. time is renormalized by the code to give the correct steady-state value. For natural circulation air flow, the code will calculate and print the inlet orifice coefficient required to give the calculated steady-state air flow rate. The code does not re-set the inlet orifice coefficient to this calculated value, since this is not always what the user would want.

A special case occurs when the user sets the steady-state sodium flow rate through the DHX to zero, indicating that the steady-state heat removal is negligible. In this case, the steady-state air flow rate is set to zero and the thermal center is set to the geometrical center.

For the steady-state initialization of the DHX, the sodium and air inlet temperatures, \(T_{\text{Nat}}\) and \(T_{\text{ab}}\), are known. Also, the sodium flow rate, \(W_{\text{Na}}\), is known. Furthermore, the correct value for the sodium outlet temperature, \(T_{\text{Nab}}\), is known from initializing the rest of the system. Therefore, the task of the DHX initialization routine is to find the air flow rate which gives the correct value of \(T_{\text{Nab}}\) in Eq. (5.6-15) This is carried out by iterating on air flow until the correct sodium outlet temperature is found.