14.2. In‑Pin Fuel Motion

14.2.1. Overview and Assumptions

When LMFBR fuel pins melt in an overpower accident, the interiors of the pins melt first and form cavities containing molten fuel and fission gas. Some of this fission gas is dissolved in the molten fuel and the remainder is free fission gas which resides in bubbles too large to be constrained by surface tension. The decrease in the void volume, caused by the density decrease of the melting fuel and also of the molten fuel, which is further heated, compresses the free fission gas and causes a hydrostatic cavity pressurization which loads the cladding. This cavity pressure increases further when more free gas becomes available due to additional fuel melting and release of dissolved gas, and when fuel vaporization occurs. This leads eventually to cladding failure. The subsequent fuel and fission‑gas ejection from the fuel pin and the local depressurization in the cavity caused by this ejection leads to fuel motion inside the pin toward the failure location. If the pin failure location for driver fuel is above the core midplane, this in‑pin fuel motion reduces reactivity; if it is near the midplane, it can cause a reactivity addition.

The concept of a pressurized molten pin cavity, which was originally developed for TOP accidents, is also reasonable for LOF accidents which lead to a power rise and fuel melting before the cladding melts. Therefore, this cavity concept is used not only in PLUTO2 but also in LEVITATE. However, in an LOF accident, leading only to a few times nominal power or less, cladding motion and fuel swelling will precede fuel melting. In this case, the fuel pin is likely to disrupt completely into a mixture of molten fuel, gas, and solid fuel chunks once fuel melting has begun. This is only modeled in LEVITATE.

The in‑pin fuel motion in the molten pin cavity in both PLUTO2 and LEVITATE is treated as a one‑dimensional, compressible flow with a time dependent and spatially variable flow cross section. The fuel/fission gas flow is considered to be homogeneous and the fission gas is assumed to be in thermal equilibrium with the fuel.

Special attention had to be given to the potentially large mass sinks due to fuel and fission‑gas ejection from the molten pin cavity. Mass sources due to fuel melt‑in which cause flow cross section changes are also considered. The fuel which is melting into the cavity brings with it dissolved (intragranular) and free (intergranular) gas. These two types of gas are treated separately in the PLUTO2 and LEVITATE in‑pin motion models. The free gas is considered not to be constrained by surface tension and to act as an ideal gas that is at the local fuel temperature. The dissolved gas, which is in the form of small bubbles, is assumed to be strongly constrained by surface tension, and its contribution to the local pressure depends on the input variable PRSFTN. If PRSFTN ≤ 10⁷ then the model assumes that the volume of the small bubbles containing the dissolved gas is negligible and thus the dissolved gas does not immediately affect the local pressure. If PRSFTN >10⁷, the pressure calculation takes into account the volume of the dissolved gas bubbles, as described in Section 14.2.6. The dissolved gas is released (coalesces) according to a decay type law using an input decay constant. The amount released during each time step is added to the free gas. The fission-gas pressure calculation takes the compressibility of the liquid fuel into account and reduces to a liquid‑fuel single‑phase pressure calculation for no fission gas and zero void volume. The total pressure includes the fission‑gas pressure and fuel vapor pressure. The fuel vapor pressure is based on the radially averaged fuel temperature.

Incoherency of the pin failures is mainly an issue in lower ramp rate TOP accidents. In these accidents, pin failure incoherency should be helpful for the post‑accident coolability. If not all pins fail in the lead assemblies during a slow TOP, some subchannels may remain open and provide coolant paths. However, if near‑midplane failures are assumed in slow TOPs in higher void worth cores, there may be a potential for exacerbating the accident due to pin failure incoherency. This is because the first pin failures will probably lead to some rapid fuel sweepout but may also cause significant voiding. Pins failing later will inject fuel into partially voided regions and this fuel may not experience rapid sweepout.

There are two major reasons for the incoherency in pin failures. One is the stochastic nature of pin failures and the other is due to differences in the power, flow, or coolant temperatures experienced by different pins. For example, the outer two fuel‑pin rows in a subassembly see colder coolant temperatures due to the proximity of the hexcan wall. Many subassemblies in an LMFBR also see considerable radial power skews. In PLUTO2 an attempt has been made to treat the stochastic pin failures by allowing different pin failure groups. However, currently only one pin group can fail, and the other two groups of pins have to remain unfailed; (see input variables NRPIl, NRPI2, and NRPI3). The treatment of the delayed fuel expulsion and in‑pin fuel motion for the two additional pin groups is not yet operational.

14.2.2. Initial Conditions for the In‑pin Calculation from DEFORM and the Pre‑Failure Pin Heat‑transfer Calculation

Before pin failure, the molten fuel/fission‑gas cavity is treated by the DEFORM pin behavior module. In the DEFORM treatment, the initially present central fuel hole is considered and the closing of this central hole due to the expansion of the molten fuel is calculated. Although DEFORM does not calculate axial fuel redistribution inside the molten cavity, an axially uniform pressure is assumed for the entire molten cavity and found by considering the total gas and volume available. (An option is also available in DEFORM to use the nodal pressures for loading the cladding. This option is relevant only for very high power situations in which the molten cavity grows to a large size within a few milliseconds.) When pin failure is predicted by DEFORM or because an input melt‑fraction or failure time have been reached, PLUTO2 is initialized from DEFORM conditions. These include the uniform cavity pressure (or the axial pressure distribution if the special DEFORM option was used), the dissolved and free fission‑gas densities, and the molten cavity geometry. However, PLUTO2 will have exactly the same cavity geometry as DEFORM only if the PLUTO2 input option FNMELT = 0.0 is chosen. This value means that the radial cavity boundary is defined by the location of the fuel solidus temperature (an assumption in DEFORM). However, it is recommended for PLUTO2 to use a higher melt fraction (FNMELT > 0.5) for the definition of the location of the cavity boundary. This is because the analysis of TREAT test E8 [14‑5, 14‑6] showed that fuel, which had not yet undergone significant melting, did not move. This can probably be explained by a high viscosity of partially molten fuel.

When the regular DEFORM option of a uniform cavity pressure is used, there is an inconsistency in the DEFORM/PLUTO2 transition due to the lack of an axial in‑pin fuel motion model in DEFORM. The nodal pressures calculated in PLUTO2 which use the pressure‑generating free fission gas and the nodal volume obtained from DEFORM can be different from the average cavity pressure. Since the latter is considered more realistic for all but very high power situations, the free fission‑gas content of the PLUTO2 nodes is adjusted to give the DEFORM calculated average cavity pressure. When the axially nonuniform pressure option in DEFORM is chosen (only relevant for very high power situations), the PLUTO2‑calculated nodal pressure can still be somewhat different from the one calculated by DEFORM and has to be slightly adjusted. This is because DEFORM takes into account the radial temperature, fuel density, and porosity profiles in the molten fuel cavity, whereas PLUTO2 uses a radially averaged temperature, fuel density and porosity in the cavity nodes. The above‑mentioned inconsistencies in the transition from DEFORM to PLUTO2 are not considered to be serious. To remove them would require the inclusion of pre‑failure in‑pin fuel motion in DEFORM and the accounting of the radial temperature profile in the molten cavity in PLUTO2 or LEVITATE.

The initialization of the PLUTO2 and LEVITATE cavity is done in subroutines PLINPT (PL UTO2 INPUT) and PLSET (PLUTO2 SETUP). DEFORM calculated cavity dimensions and free and dissolved fission‑gas densities are transferred to PLUTO2 in these routines. Also, the radially averaged cavity temperatures are determined from the temperature profiles obtained from the heat‑transfer routines, TSHTRN or TSHTRV.

14.2.3. Coupling of the In‑pin Motion Calculation with the PLHTR Heat Transfer Calculation

For the calculation of the growth of the molten fuel cavity, it is important that a fuel temperature calculation is performed in the solid fuel surrounding the molten fuel cavity. This temperature calculation is performed with the PLHTR (PLUTO2 HEAT TRANSFER) routine which is a modified version of the transient heat‑transfer subroutine TSHTRV. (The latter is used to calculate fuel‑pin temperatures during the sodium boiling phase of a LOF accident). In the PLHTR heat conduction calculation, the fuel node adjacent to the molten cavity boundary receives heat from the molten cavity in the form of a heat source. This heat source is the total energy convected to the cavity wall from the molten fuel flow during a heat‑transfer time step divided by the heat‑transfer time‑step size. If a solid fuel node reaches the input melt fraction criterion FNMELT, this node will be gradually added to the molten cavity. The rate of fuel addition depends on the temperature gradient between the node adjacent to the cavity wall and its neighboring solid fuel node.

14.2.4. Overview of the Numerical Approach for the In‑pin Fuel Motion Calculation and Description of Subroutines PLlPIN and PL2PIN

There are several requirements for the solution algorithm for this one dimensional, compressible flow problem with variable flow cross section: (a) it had to be able to handle large mass sinks (due to fuel ejection from the pins), (b) it had to conserve mass perfectly, and (c) it had to run efficiently. This was achieved with a predominantly explicit Eulerian solution method. All convection mass, energy, and momentum fluxes are treated explicitly (i.e., the beginning of time‑step values are used). However, the solution sequence of the different equations introduces a certain implicitness which is of importance for treating the strong mass sinks.

For the in‑pin motion calculation three mass, one energy and one momentum conservation equations are solved. The mass conservation equations are for the fuel and the free and the dissolved fission gas. The fuel and free fission‑gas mass conservation equations are solved first, followed by the fuel energy conservation equation. The fission‑gas temperature change is assumed to be the same as the fuel temperature change. From the results of the mass and energy conservation equations, a new pressure is calculated. This is not the true end‑of‑time‑step pressure because the velocity changes during the time step have not been included. However, it is a proper prediction for the end‑of‑time‑ step value in an explicit sense. In the fuel‑ejecting nodes, this new pressure and the advanced densities and energies are used for calculating the fuel and fission‑gas ejection rates. The pressure in the ejection nodes is then decreased in order to account for the fuel and gas losses. The adjusted new pressures are then used in the fuel/fission‑gas momentum equation. There is an input option in PLUTO2 to use a combination of the new and the old pressures. This option lets the pressure, \(P\), be:

(14.2-1)\[ P = \left( 1 - \text{EPCH} \right) \cdot \text{beginning-of-time-step pressure} + \text{EPCH} \cdot \text{advanced pressure}\]

The recommended input value is \(\text{EPCH} = 1\) because the calculation remained stable for longer time steps in test problems involving shock propagation and shock reflection when this input value was used [14‑21]. In these test calculations, it was also attempted to iterate on the convective fluxes by repeating most of the in‑pin calculation for each time step. This seemed to make the results somewhat smoother, but did not allow a time step as long as the one allowable with the above‑described explicit scheme.

The time‑step criterion in this compressible calculation is the sonic Courant condition. This does not require particularly small time steps because the sonic velocity in two‑phase mixtures is fairly low for the void fractions encountered in pin blowdown calculations.

A staggered numerical grid with the densities, energies, and temperatures defined at the cell centers and the velocities at the cell edges is used. The spatial differencing uses full donor cell differencing. Although this is not as accurate as higher order differencing, it makes the calculation stable because it introduces a numerical diffusion effect. It is interesting to note that this stabilizing effect was not enough to keep two‑phase test calculations stable for shock reflections from a rigid wall. Although these test calculations could be stabilized by introducing an artificial viscous pressure into the calculations [14‑21], the artificial viscous pressure is not necessary for regular pin blowdown calculations. It could even cause problems if the input constants, which affect the magnitude of the artificial viscous pressure, are set too high. The two relevant input parameters, ClVIPR and C2VIPR, should therefore be set to small values such as \(10^{-3}\).

The free fission‑gas mass conservation, the fuel mass conservation, and the fuel energy equation are solved in subroutine PLlPIN (PLUTO2 1st PIN ROUTINE). PLlPIN also computes the molten cavity geometry changes due to fuel melt‑in, and the fuel and fission‑gas ejection from the pins (see Section 14.3). The fuel/fission‑gas momentum equation and the dissolved fission‑gas mass equation are solved in PL2PIN (PLUTO2 2nd PIN ROUTINE). This routine also calculates the sonic velocities for each node. The minimum time step found is the predicted time step for the next cycle. However, the actual PLUTO2 time step, which is used both in the pin and in the channel calculation, is the smaller of the pin and channel hydrodynamics time steps. The channel time step is usually the smaller one, and thus, dominates the time‑step selection.

14.2.5. Definition of the Generalized Smear Densities for the In‑pin Calculation

The use of generalized smear densities in PLUTO2 (and LEVITATE) has been prompted by the many different moving and stationary components in this problem. Its use also simplifies the differential and finite difference equations for variable cross section flow. The pie chart in Figure 14.2.1 gives an example of the relative cross sectional areas within a subassembly or experimental loop at a certain axial elevation.

If the total area of the subassembly is AXMX, the generalized volume fraction of a certain component \(k\) is:

(14.2-2)\[ \theta_{\text{k}}\left( z,t \right) = \frac{A_{\text{k}}\left( z,t \right)}{\text{AXMX}}\]

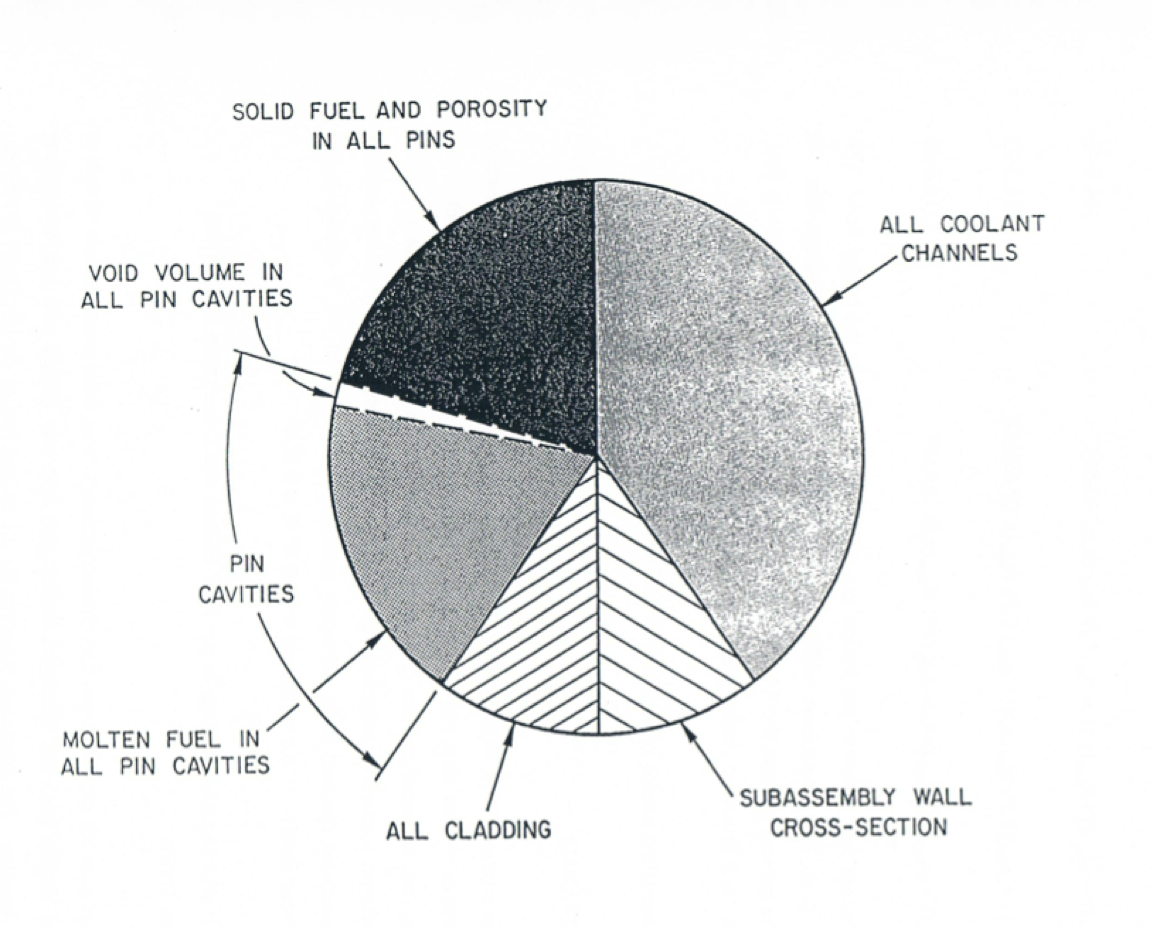
Figure 14.2.1 The Left-hand Side of This Pie Chart Illustrates the Possible Material Cross Sectional Areas in the Fuel Pin, the Whole Pie Representing an Area AXMW Which is an Input Parameter

where \(A_{\text{k}}\) is the cross sectional area occupied by component \(k\) (the latter refers, e.g., to the cavities or the moving fuel in all failed pins within the subassembly cross section). The reference area AXMX, which is an input quantity, can be arbitrarily chosen. This is because the code is invariant to the choice of AXMX (i.e., as long as it is not varied by several orders of magnitude which can lead to differences due to truncation errors). However, the recommended value of AXMX is the cross sectional area of a subassembly or experiment test section (including the can wall) because the volume fractions of the different components that appear in the PLUTO2 output are better understood in this case.

The generalized volume fraction of the free fission gas and fuel vapor in the cavity is the difference between the cavity volume fraction and the fuel volume fraction.

(14.2-3)\[ \theta_{\text{fica}}\left( z,t \right) = \theta_{\text{ca}}\left( z,t \right) - \theta_{\text{fuca}}\left( z,t \right)\]

where

\(\theta_{\text{fica}}\) = generalized volume fraction of the free fission gas and fuel vapor in the cavities of the failed pins.

\(\theta_{\text{ca}}\) = generalized volume fraction of the molten cavities in all failed pins which can be calculated from \(A_{\text{ca}} \big/ \text{AXMX}\)

\(\theta_{\text{fuca}}\) = generalized volume fraction of the fuel in the cavities of all failed pins

Generalized smear densities, which are always marked by a prime, are defined as products of physical densities and generalized volume fractions:

(14.2-4)\[ {\rho'}_{\text{fuca}} \left( z,t \right) = \rho_{\text{fuca}}\left( T \right)\theta_{\text{fuca}}\left( z,t \right) = \frac{\rho_{\text{fuca}}\left( T \right) A_{\text{fuca}}\left( z,t \right)}{\text{AXMX}}\]

(14.2-5)\[ {\rho'}_{\text{fica}} \left( z,t \right) = \rho_{\text{fica}}\left( T,P \right)\theta_{\text{fica}}\left( z,t \right) = \frac{\rho_{\text{fica}}\left( T,P \right) A_{\text{fica}}\left( z,t \right)}{\text{AXMX}}\]

(14.2-6)\[ {\rho'}_{\text{fsca}} \left( z,t \right) = \rho_{\text{fsca}}\left( z,t \right)\theta_{\text{fuca}}\left( z,t \right) = \frac{\rho_{\text{fsca}}\left( z,t \right) A_{\text{fuca}}\left( z,t \right)}{\text{AXMX}}\]

where the subscript \(\text{fsca}\) refers to the fission gas which is dissolved in the cavity fuel. The temperature \(T\) is the fuel temperature, which should actually be written with subscript \(\text{fuca}\). It should again be pointed out that the A’s refer to total cross section areas of all the cavity fuel, free fission gas, and dissolved fission gas in the failed pins of one subassembly.

The generalized source or sink term is written as:

(14.2-7)\[ S' = \frac{S^{l}}{\text{AXMX}}\]

where the source or sink term \(S^{l}\) represents a mass source or sink per unit time and unit length. The primed source or sink term has the dimension of mass per unit time and per unit smear volume. This unit of smear volume is a \(m^{3}\) of the cell volume \(\text{AXMX} \cdot \Delta z\) in which all relevant components (including components in all failed pins, the components in all the channels and the structure) are assumed to be uniformly smeared. From Eq. (14.2-7), a change in the generalized smear density \(\rho'\) due to source or sink \(S'\) it just \(S' \Delta t\).

14.2.6. Differential Equations for the In-pin Fuel Motion and Description of Sink and Source Terms

The equation set for the in-pin fuel motion includes three mass conservation equations (for fuel, free fission gas, and dissolved fission gas) and one energy and one momentum conservation equation. The continuity equation for the molten fuel in the pin cavity is written:

(14.2-8)\[ \frac{\partial}{\partial \text{t}}(\rho_{\text{fuca}}A_{\text{fuca}}) = - \frac{\partial}{\partial \text{z}}\left( \rho_{\text{fuca}}A_{\text{fuca}} u_{\text{fuca}} \right) + S_{\text{fuca},\text{me}}^{l}\left( z,t \right) - S_{\text{fuca},\text{ej}}^{l}\left( z,t \right)\]

where the subscripts \(\text{me}\) and \(\text{ej}\) refer to fuel melting into and fuel ejection from the pin cavities of all failed pins, respectively. By dividing by AXMX and using the definitions of the generalized smear densities and source and sink terms, Eq. (14.2-8) becomes:

(14.2-9)\[ \frac{\partial}{\partial \text{t}}{\rho'}_{\text{fuca}} = - \frac{\partial}{\partial \text{z}}\left( {\rho'}_{\text{fuca}} u_{\text{fuca}} \right) + {S'}_{\text{fuca},\text{me}} - {S'}_{\text{fuca},\text{ej}}\]

where the primed sources and sinks are per unit time and per unit smear volume (see Eq. (14.2-7)). The integrated source term, \(S'_{\text{fuca,me}} \Delta t_{\text{PL}}\), which is actually needed in the finite difference equations of the code, is calculated from

(14.2-10)\[ {S'}_{\text{fuca},\text{me}}\Delta t_{\text{PL}} = \rho_{\text{fu},\text{cabd}}\Delta A_{\text{me}} \text{NRPI} \cdot \frac{\text{FNPI}}{\text{AXMX}}\]

here

\(\Delta t_{\text{PL}}\) = PLUTO2 time step

\(\rho_{\text{fu,cabd}}\) = fuel density (including porosity) adjacent to the cavity boundary,

\(\Delta A_{\text{me}}\) = area of fuel (including porosity) melted into the cavity per PLUTO2 time step per pin

\(\text{NRPI}\) = number of pins per subassembly,

\(\text{FNPI}\) = fraction of the pins which are failed.

When the solid fuel node adjacent to the cavity has not yet exceeded an input melt fraction value FNMELT:

(14.2-11)\[ {S'}_{\text{fuca,me}} \Delta t_{\text{PL}} = 0\]

The \(\Delta A_{\text{me}}\) in Eq. (14.2-10) is related to a change in the cavity diameter by

(14.2-12)\[ \Delta A_{\text{me}} = \frac{\pi}{4}\Delta D_{\text{ca}}\left( 2D_{\text{ca}} + \Delta D_{\text{ca}} \right)\]

In order to avoid adding the whole radial node instantaneously upon meeting the input melt fraction criterion FNMELT, the radial node is added gradually beginning at the time FNMELT is reached and the addition is completed once the melt fraction has exceeded \(\text{FNMELT} + 0.1\). Once the melt fraction has become greater than FNMELT, the change in cavity diameter is calculated from

(14.2-13)\[ \Delta D_{\text{ca}} = \text{FNMECA} \cdot 2 \cdot \Delta r_{\text{node}}\]

where \(\Delta r_{\text{node}}\) is the width of the heat-transfer node adjacent to the cavity wall before it is melted into the cavity. FNMECA is the fraction of this node width that has melted into the cavity per PLUTO2 time step.

(14.2-14)\[ \text{FNMECA} = \frac{\Delta t_{\text{PL}}\left( \frac{\left( T_{\text{cabd}}^{n + 1} - T_{\text{cabd}}^{n} \right)}{\Delta t_{\text{Ht}}} \right)}{\left( 0.1 \cdot \left( T_{\text{fu,liq}} - T_{\text{fu,sol}} \right) \right)} \ = \frac{\Delta T_{\text{PL}}}{\left( 0.1 \cdot \left( T_{\text{fu,liq}} - T_{\text{fu,sol}} \right) \right)}\]

where

\(T_{\text{cabd}}^{n}, T_{\text{cabd}}^{n + 1}\) are the temperatures of the fuel node adjacent to the cavity at the beginning and at the end of the heat-transfer time step \(\Delta t_{\text{Ht}}\), respectively.

\(T_{\text{fu},\text{liq}}, T_{\text{fu},\text{sol}}\) are fuel liquidus and solidus temperatures, respectively. The difference between the two is the melting band width.

\(\Delta t_{\text{PL}}\) is the PLUTO2 time step.

\(\Delta T_{\text{PL}}\) is the temperature change of the fuel adjacent to the cavity during a PLUTO2 time step.

Eq. (14.2-14) implies that the whole heat-transfer node will be melted into the cavity after its temperature has risen by 1/10 of the melting band width beyond the input value FNMELT. Moreover, it is checked whether the neighboring solid fuel node also has exceeded the input melt fraction criterion FNMELT. If this is the case, the entire remaining node currently melting into the cavity is added immediately to the cavity. This situation can occur in TREAT experiments.

The sink term \({S'}_{\text{fuca,ej}}\) that is due to fuel ejection is also the source term for the coolant channel equations. It will be described in detail in Section 14.3. Its integrated form is similar to Eq. (14.2-10)

(14.2-15)\[ {S'}_{\text{fuca},\text{ej}} \cdot \Delta t_{\text{PL}} = {\rho'}_{\text{fuca}} \cdot \text{FN}\]

where

\(\text{FN}\) = fraction of the fuel in an ejecting cavity cell that is actually ejected during a PLUTO2 time step.

The free fission-gas mass conservation equation is written

(14.2-16)\[ \frac{\partial}{\partial \text{t}}\left( \rho_{\text{fica}}A_{\text{fica}} \right) = - \frac{\partial}{\partial \text{z}}\left( \rho_{\text{fica}}A_{\text{fica}}u_{\text{fuca}} \right) + S_{\text{fica},\text{me}}^{l}\left( z,t \right) - S_{\text{fica},\text{ej}}^{l} + S_{\text{fsca,rl}}^{l}\]

where the subscripts \(\text{fsca}\) and \(r l\) refer to fission gas in solution and to the release of this dissolved fission gas, respectively. Dividing by AXMX and by using the definition of the generalized smear densities and source and sink terms yields

(14.2-17)\[ \frac{\partial}{\partial \text{t}}{\rho'}_{\text{fica}} = - \frac{\partial}{\partial \text{z}}\left( {\rho'}_{\text{fica}} u_{\text{fuca}} \right) + S_{\text{fica},\text{me}}^{l} - S_{\text{fica,ej}}^{l} + S_{\text{fsca,rl}}^{l}\]

The integrated source term for free fission gas due to fuel melt-in is similar to that in Eq. (14.2-10):

(14.2-18)\[ {S'}_{\text{fica,me}} \Delta t_{\text{PL}} = \rho_{\text{fifs,cabd}} \Delta A_{\text{me}} \left( \text{NRPI} \cdot \frac{\text{FNPI}}{\text{AXMX}} \right) \cdot \text{FIFNGB}\]

where \(\Delta A_{\text{me}}\) is the calculated change in cavity cross sectional area described before (see Eq. (14.2-12)), \(\rho_{\text{fifs,cabd}}\) is the density of all the gas in the fuel node adjacent to the cavity, and FIFNGB is an input parameter determining the fraction of all the gas entering the cavity with the molten fuel which instantaneously becomes free gas. This is an input parameter because DEFORM does not currently discriminate between intra-granular and grain-boundary gas. The ratio of the grain-boundary gas to the total gas in a node may be similar to the fraction of the gas that becomes free upon melting into the cavity. However, it seems more likely that only a smaller fraction will be instantaneously available because some of the grain-boundary bubbles may not be large enough to be considered free gas as soon as the fuel melts.

The quantity \(\rho_{\text{fifs,cabd}}\) is calculated from:

(14.2-19)\[ \rho_{\text{fifs,cabd}} = \text{RETFG2}_{\text{cabd}} \frac{\left( \frac{\text{FUMS}_{\text{cabd}}}{\text{FUELM}} S_{\text{cabd}} \right)}{\text{VOLUME}_{\text{cabd}}}\]

where

\(\text{RETFG2}_{\text{cabd}}\) is the total retained fission-gas mass in the original radial fuel-pin node at the cavity boundary before it has actually melted in,

\(\text{FUMS}_{\text{cabd}}\) is is the current fuel mass in the melting radial fuel-pin node at the cavity boundary,

\(\text{FUELMS}_{\text{cabd}}\) is the original fuel mass of the radial fuel-pin node at the cavity boundary before any fuel is removed due to melt-in,

\(\text{VOLUME}_{\text{cabd}}\) is the current volume of the melting radial fuel-pin node at the cavity boundary.

The free fission-gas sink term due to fuel ejection in Eq. (14.2-17) is described in detail in Section 14.3. Its form is similar to that of the sink term for fuel ejection Eq. (14.2-15):

(14.2-20)\[ {S'}_{\text{fica,ej}} \cdot \Delta t_{\text{PL}} = {\rho'}_{\text{fica}} \cdot \text{FN}\]

The term \(\text{FN}\) used in this equation is the same as in Eq. (14.2-15) because it is assumed in PLUTO2 that fission gas and fuel are ejected with the same volume fractions that exist in the ejecting cavity node.

The source term due to dissolved fission-gas release in Eq. (14.2-17) is:

(14.2-21)\[ {S'}_{\text{fsca},\text{r}l} = {\rho'}_{\text{fsca}} \cdot \text{CIRTFS}\]

where CIRTFS is a release constant for dissolved fission gas which is input and has the dimensions \(s^{-1}\). (The same release constant is also used for the dissolved fission-gas release in the coolant channels - see Eq. (14.4-20)). This is a relatively simple exponential decay-type approach to treat the release of the gas dissolved in molten fuel. However, the understanding of the mechanism of dissolved gas release from molten fuel is still very limited.

The dissolved fission-gas mass conservation equation is:

(14.2-22)\[ \frac{\partial}{\partial \text{t}}\left( \rho_{\text{fsca}} A_{\text{fuca}} \right) = - \frac{\partial}{\partial \text{z}}\left( \rho_{\text{fsca}} A_{\text{fuca}} u_{\text{fuca}} \right) + S_{\text{fsca,me}}^{l} - S_{\text{fsca,ej}}^{l} - S_{\text{fsca,rl}}^{l}\]

By dividing this equation by \(\text{AXMX}\) and using the definitions of the generalized smear density and sources and sinks, one obtains:

(14.2-23)\[ \frac{\partial}{\partial \text{t}}{\rho'}_{\text{fsca}} = - \frac{\partial}{\partial \text{z}}\left( {\rho'}_{\text{fica}} u_{\text{fuca}} \right) + S_{\text{fsca,me}}^{l} - S_{\text{fsca,ej}}^{l} - S_{\text{fsca,rl}}^{l}\]

where

(14.2-24)\[ {S'}_{\text{fsca,me}} = {S'}_{\text{fica,me}} \frac{\left( 1 - \text{FIFNGB} \right)}{\text{FIFNGB}}\]

and \(S'_{\text{fica,me}}\) and FIFNGB are defined for Eq. (14.2-18). The ejection term is connected to the one for the free fission-gas ejection, which is given in Eq. (14.2-20):

(14.2-25)\[ {S'}_{\text{fsca,ej}} = {S'}_{\text{fica,ej}}\frac{{\rho'}_{\text{fsca}}}{{\rho'}_{\text{fica}}}\]

The absolute value of the sink term due to the dissolved fission-gas release has been described in Eq. (14.2-21).

The fuel energy conservation equation is written:

(14.2-26)\[\begin{split}\frac{\partial}{\partial \text{t}}\left( \rho_{\text{fuca}} e_{\text{fuca}} A_{\text{fuca}} \right) = & - \frac{\partial}{\partial \text{z}}\left( \rho_{\text{fuca}} e_{\text{fuca}} A_{\text{fuca}} u_{\text{fuca}} \right) + S_{\text{fuca,me}}^{l} e_{\text{fu,cabd}} \\ & - {S'}_{\text{fuca,ej}} e_{\text{fuca}} + Q A_{\text{fuca}}\rho_{\text{fuca}} \\ & - h_{\text{fuca,cabd}} \cdot \left( T_{\text{fuca}} - T_{\text{fu,cabd}} \right) \pi D_{\text{ca}} \text{NRPI} \cdot \text{FNPI}\end{split}\]

Dividing Eq. (14.2-26) by AXMX and using the definitions of the generalized smear densities and sources and sinks produces:

(14.2-27)\[\begin{split}\frac{\partial}{\partial \text{t}}\left( {\rho'}_{\text{fuca}} e_{\text{fuca}} \right) = & - \frac{\partial}{\partial \text{z}}\left( {\rho'}_{\text{fuca}} e_{\text{fuca}} u_{\text{fuca}} \right) + {S'}_{\text{fuca,me}} e_{\text{fu,cabd}} \\ & - S_{\text{fuca,ej}}^{l} e_{\text{fuca}} + Q {\rho'}_{\text{fuca}} \\ & - h_{\text{fuca,cabd}} \cdot \left( T_{\text{fuca}} - T_{\text{fu,cabd}} \right) \pi D_{\text{ca}} \text{NRPI} \cdot \frac{\text{FNPI}}{\text{AXMX}}\end{split}\]

By rewriting the left-hand side of Eq. (14.2-27) as

(14.2-28)\[\frac{\partial}{\partial \text{t}}\left( {\rho'}_{\text{fuca}}e_{\text{fuca}} \right) = {\rho'}_{\text{fuca}}\frac{\partial}{\partial \text{t}} e_{\text{fuca}} + e_{\text{fuca}} \frac{\partial}{\partial \text{t}} {\rho'}_{\text{fuca}}\]

and by using the mass conservation Eq. (14.2-8), one obtains

(14.2-29)\[\begin{split}{\rho'}_{\text{fuca}}\frac{\partial}{\partial \text{t}}e_{\text{fuca}} = & - \frac{\partial}{\partial \text{z}}\left( {\rho'}_{\text{fuca}}e_{\text{fuca}}u_{\text{fuca}} \right) + e_{\text{fuca}} \frac{\partial}{\partial \text{z}} \left( {\rho'}_{\text{fuca}} u_{\text{fuca}} \right) \\ & + {S'}_{\text{fuca,ej}} \left( e_{\text{fu,cabd}} - e_{\text{fuca}} \right) + Q {\rho'}_{\text{fuca}} \\ & - h_{\text{fuca,cabd}}\left( T_{\text{fuca}} - T_{\text{fu,cabd}} \right) \pi D_{\text{ca}} \text{NRPI} \cdot \frac{\text{FNPI}}{\text{AXMX}}\end{split}\]

where \(Q\) is the fission heat source per kg of fuel

(14.2-30)\[Q = \text{FNPOHE} \cdot \text{POW} \cdot \text{PSHAPE} \left( K \right) \cdot \left( 1 - \text{GAMSS} - \text{GAMTNC} - \text{GAMTNE} \right) \cdot \frac{F_{\text{POWER}}}{\text{FUMASS}\left( K \right)}\]

In Eq. (14.2-30),

(14.2-31)\[\text{FNPOHE} = \exp\left\lbrack \text{POWCOF}\left( 1 \right) + \Delta t\left( \text{POWCOF}\left( 2 \right) + \Delta t_{\text{x}}\text{POWCOF}\left( 3 \right) \right) \right\rbrack\]

where \(\Delta t_{\text{x}}\) is the time between the current PLUTO2 time and the beginning of the current main (point kinetics) time step. The POWCOF’s are the coefficients that are found by fitting an exponential function to the power levels at the end of the last three point kinetics time step.

\(\text{POW}\) = steady-state power in the peak axial fuel-pin segment (see SAS4A input description)

\(\text{PSHAPE} \left( K \right)\) = ratio of pin power at axial node \(K\) to POW (see SAS4A input description)

\(\text{GAMSS, GAMTNC, GAMTNE}\) = fractions of total power for the direct heating of structure, coolant, and cladding, respectively. (See SAS4A input description)

\(\text{FUMASS} \left( K \right)\) = initial total fuel mass in axial pin segment \(K\)

\(F_{\text{POWER}}\) = power reduction factor if there is a radial power gradient in the pin (as is common in TREAT experiments):

(14.2-32)\[F_{\text{POWER}} = \frac{\sum_{\text{I=1}}^{I_{\text{cabd}}}{\text{PSHAPR}\left( I \right) \cdot \text{FUELMS}\left( I,K \right) \big/ \ \sum_{\text{I=1}}^{I_{\text{cabd}}}{\text{FUELMS}\left( I,K \right)}}}{\sum_{\text{I=1}}^{\text{NT}}{\text{PSHAPR}\left( I \right) \ \cdot \text{FUELMS}\left( I,K \right) \big/ \sum_{\text{I=1}}^{\text{NT}}{\text{FUELMS}\left( I,K \right)}}}\]

where

\(\text{NT}\) = number of radial pin nodes

\(I_{\text{cabd}}\) = number of radial pin nodes in the cavity

\(\text{PSHAPR} \left( I \right)\) = mass normalized radial power distribution in radial node \(I\) (See SAS4A input description)

\(\text{FUELMS} \left( I,K \right)\) = initial fuel mass in the radial fuel-pin node \(I\), \(K\).

The heat-transfer coefficient in Eq. (14.2-26) is the sum of a convective and a conduction heat transfer term.

\[h_{\text{fuca},\text{cabd}} = \left( h_{1} + h_{2} \right)\]

where

(14.2-33)\[h_{1} = \frac{k_{\text{fu}}}{D_{\text{ca}}} \cdot \text{St} \cdot \text{Pr} \cdot \text{Re}\]

This comes from the definition of the Nusselt number

(14.2-34)\[\text{Nu} = \text{St} \cdot \text{Pr} \cdot \text{Re}\]

where

St = Stanton number = \(\frac{h}{\left( \rho u C_{\text{p}} \right)}\)

Pr = Prandtl number = \(\mu \frac{C_{\text{p}}}{k}\)

Re = Reynolds numbers = \(D \frac{\rho u}{\mu}\)

The Deissler correlation [14-22, 14-23] was used for finding the relationship between the three nondimensional numbers on the right-hand side of Eq. (14.2-34). The Prandtl number for fuel is about 2.2. By using this value in the Deissler correlation, it can be shown that

(14.2-35)\[\text{St} \approx 0.0158 \text{Re}^{- 0.2}\]

By using Eq. (14.2-8) and the definition of the Prandtl number,

(14.2-36)\[h_{1} = \frac{1}{D_{\text{ca}}} \cdot \mu_{\text{fu,liq}} \cdot C_{\text{p,fu}} \cdot \text{CIA3} \cdot \text{Re}_{\text{ca}}^{0.8}\]

where

\(k_{\text{fu}}\) = conductivity of fuel which is input (CDFU)

\(\mu_{\text{fu,liq}}\) = liquid fuel viscosity which is input (VIFULQ)

\(\text{CIA3}\) = input constant. A value of 0.0158 is recommended because of

(14.2-37)\[\text{Re}_{\text{ca}} = \frac{\left( \frac{\left| u_{\text{fuca}} \right| D_{\text{ca}} {\rho'}_{\text{fuca}}}{\theta_{\text{ca}}} \right)}{\mu_{\text{fu,liq}}}\]

The conduction heat-transfer coefficient, \(h_{2}\), which is relevant for a low flow or a stagnant flow condition (the stagnant condition is assumed in the simplified PLUTO2 node — see Section 14.1.2), is of the following form

(14.2-38)\[h_{2} = \frac{k_{\text{fu}}}{D_{\text{ca}}}4\]

The pressure calculation in the fuel-pin cavity is based on the assumption that the fission-gas pressure and fuel-vapor pressure can be added. The total cavity pressure is:

(14.2-39)\[P_{\text{ca}} = P_{\text{fica}}\left( T_{\text{fuca}}, {\rho}_{\text{fica}} \right) + P_{\text{fvca}} \left( T_{\text{fuca}} \right)\]

where the fission-gas pressure is calculated form a special form of the ideal-gas equation which takes the compressibility of the liquid fuel into account:

(14.2-40)\[P_{\text{fica}} = \frac{R_{\text{fi}} \cdot T_{\text{fuca}}{\rho'}_{\text{fica}}}{\left( \theta_{\text{ca}} - \theta_{\text{fuca}} + \theta_{\text{fuca}} K_{\text{fu}} \cdot P_{\text{fica}} \right)}\]

where

\(R_{\text{fi}}\) = the universal gas constant divided by the molecular weight of the mixture of fission gas and helium fill gas. \(R_{\text{fi}}\) is equal to an input value RGAS which should take into account the relative amounts of krypton, xenon, and helium. The latter may be important for near-fresh fuel.

\(K_{\text{fu}}\) = liquid fuel compressibility which is input (see CMFU).

The physically reasonable solution of the quadratic Eq. (14.2-40) is:

(14.2-41)\[P_{\text{fica}} = \frac{- \left( \theta_{\text{ca}} - \theta_{\text{fuca}} \right) + \sqrt{\left( \theta_{\text{ca}} - \ \theta_{\text{fuca}} \right)^{2} + 4\theta_{\text{fuca}} K_{\text{fu}} \cdot R_{\text{fi}} \ \cdot T_{\text{fuca}} {\rho'}_{\text{fica}}}}{2 \theta_{\text{fuca}} K_{\text{fu}}}\]

There is also a second solution with a minus sign in front of the square root, which does not give a physically reasonable result. Eq. (14.2-41) reduces to a single-phase liquid pressure solution for no fission gas and \(\theta_{\text{fuca}} > \theta_{\text{ca}}\):

(14.2-42)\[P_{\text{fica}} = - \frac{\left( \theta_{\text{ca}} - \theta_{\text{fuca}} \right)}{\left( \theta_{\text{fuca}}K_{\text{fu}} \right)}\]

which is equivalent to the definition of the fuel compressibility. For void fractions greater than 30% the fission-gas pressure is calculated from a modified Eq. (14.2-40) in which the term with \(K_{\text{fu}}\) is dropped.

If the dissolved fission gas present in the molten fuel cavity is assumed to occupy a negligible volume, in comparison with the volume occupied by the free gas then the \(\theta_{\text{fuca}}\) in Eq. (14.2-40) and 14.2-34 reflects the actual volume occupied by the molten fuel. This assumption is justified when the ambient cavity pressure is significantly smaller than the bubble surface tension pressure, as was the case in all TREAT experiments analyzed with SAS4A. When this assumption is used, the dissolved fission gas does not affect the cavity pressure until it is released, in a gradual manner, to the free gas field.

However, during a transient characterized by a rapid increase in the power level, the cavity pressures can reach higher values, so that the influence of the dissolved fission gas becomes important. In order to address this issue the dissolved fission gas modeling in the pin cavity was introduced as described below.

The dissolved fission gas is assumed to exist in the form of small bubbles, with the gas inside the bubbles at the pressure \(P_{\text{bubble}}\):

\(P_{\text{bubble}} = P_{\text{surface tension}} + P_{\text{cavity}}\).

The quantity \(P_{\text{surface tension}}\) is an input to the code (PRSFTN). Its value can be determined as:

\[P_{\text{surface tension}} = \frac{2\sigma}{r},\]

where:

\(\sigma\) = bubble surface tension,

\(r\) = bubble radius.

The recommended value for \(P_{\text{surface tension}}\) is \(4 \times 10^{7}\) Pa, corresponding to \(\sigma = 0.4\) N/m (400 dyne/cm) and \(r = 2 \times 10^{-8}\) m (200 Å). The surface tension pressure is assumed to remain constant during the calculations. Furthermore, in order to simplify the calculations, the pressure \(P_{\text{cavity}}\) used in the calculation of the bubble pressure \(P_{\text{bubble}}\) is the cavity pressure at the end of the previous time step. The volume occupied by the dissolved gas in the axial cavity cell i is then calculated using the equation:

\[V_{\text{D,i}} = \frac{M_{\text{D,i}} \cdot R \cdot T_{\text{i}}}{m \cdot P_{\text{bubble,i}}} = \frac{R}{m} \cdot \frac{M_{\text{D,i}} \cdot T_{\text{i}}}{P_{\text{bubble,i}}}\]

where:

\(M_{\text{D,I}}\) = mass of dissolved fission gas in cell \(i\),

\(\frac{R}{m}\) = universal gas constant divided by molar mass,

\(T_{\text{i}}\) = gas temperature in cell \(i\), assumed to be equal to the molten fuel temperature,

\(P_{\text{bubble,I}}\) = the pressure of the gas contained in the small bubbles, calculated above.

The fuel and dissolved gas are assumed to form a homologous mixture, with the volume given by:

\[V_{\text{fuel}}^{\text{mixture}} = V_{\text{fuel,i}} + V_{\text{D,i}},\]

where:

\(V_{\text{fuel,I}}\) = molten fuel volume in cell \(i\),

\(V_{\text{D,i}}\) = dissolved gas volume in cell \(i\).

The calculation then proceeds as before, using the volume \(V_{\text{fuel,i}}^{\text{mixture}}\) instead of \(V_{\text{fuel,i}}\) to determine the value of \(\theta_{\text{fuca}}\) used in Eq. (14.2-40) and Eq. (14.2-41).

When there is little molten fuel in an axial cavity cell, i.e., the gas occupies a large fraction of the cell volume, a perfect gas equation is used to determine the free gas pressure. The underlying assumption is that the compressibility of the fuel/dissolved-gas-mixture has a negligible effect under these circumstances. However, if larger amounts of molten fuel are present, the pressure calculation takes into account the molten fuel compressibility. In this case, the dissolved fission gas and molten fuel volumes are lumped together and assumed to have the same compressibility as the molten fuel. This is a simplifying assumption, but is conservative in the sense that the molten fuel/dissolved gas mixture is likely to have a higher compressibility than the molten fuel itself and thus would lead to somewhat lower cavity pressures during rapid power excursions.

This treatment of the dissolved fission gas has also been implemented in DEFORM-4, LEVITATE, and PLUTO2. If the input constant PRSFTN is less than \(10^{7}\) the effect of the dissolved fission gas on the ambient pressure is ignored.

The momentum conservation equation for the fuel/fission-gas mixture is:

(14.2-43)\[\begin{split}\frac{\partial}{\partial \text{t}}\left( \rho_{\text{fuca}}A_{\text{fuca}}u_{\text{fuca}} + \rho_{\text{fica}}A_{\text{fica}}u_{\text{fuca}} \right) \\ = - \frac{\partial}{\partial \text{z}} \left( \rho_{\text{fuca}} A_{\text{fuca}}u_{\text{fuca}}^{2} + \rho_{\text{fica}}A_{\text{fica}}u_{\text{fuca}}^{2} \right) \\ - A_{\text{ca}} \cdot \left( \frac{\partial \text{P}_{\text{ca}}}{\partial \text{z}} + \frac{\partial \text{P}_{\text{vi}}}{\partial \text{z}} \right) - g \left( \rho_{\text{fuca}} A_{\text{fuca}} + \rho_{\text{fica}}A_{\text{fica}} \right) \\ - u_{\text{fuca}} \left| u_{\text{fuca}} \right| \cdot \left( \rho_{\text{fuca}} \frac{A_{\text{fuca}}}{A_{\text{ca}}} + \rho_{\text{fica}} \frac{A_{\text{fica}}}{A_{\text{ca}}} \right) \frac{A_{\text{ca}} \cdot F_{\text{friction}}}{\left( 2D_{\text{ca}} \right)} \\ - \left( S_{\text{fuca,ej}}^{l} + S_{\text{fica,ej}}^{l} \right) u_{\text{fuca}}\end{split}\]

Dividing Eq. (14.2-43) by AXMX and using the definitions for the generalized smear densities and mass sinks gives:

(14.2-44)\[\begin{split}\frac{\partial}{\partial \text{t}}\left\lbrack u_{\text{fuca}}\left( {\rho'}_{\text{fuca}} + {\rho'}_{\text{fica}} \right) \right\rbrack = \frac{\partial}{\partial \text{z}}\left\lbrack u_{\text{fuca}}^{2}\left( {\rho'}_{\text{fuca}} + {\rho'}_{\text{fica}} \right) \right\rbrack \\ - \theta_{\text{ca}} \left( \frac{\partial \text{P}_{\text{ca}}}{\partial \text{z}} + \frac{\partial \text{P}_{\text{vi}}}{\partial \text{z}} \right) - g \left( {\rho'}_{\text{fuca}} + {\rho'}_{\text{fica}} \right) \\ - u_{\text{fuca}} \left| u_{\text{fuca}} \right| \cdot \left( {\rho'}_{\text{fuca}} + {\rho'}_{\text{fica}} \right) \frac{F_{\text{friction}}}{\left( 2D_{\text{ca}} \right)} \\ - \left( {S'}_{\text{fuca,ej}} + {S'}_{\text{fica,ej}} \right) u_{\text{fuca}}\end{split}\]

\(u_{\text{fuca}}\) = vertically upward fuel velocity in the cavity (see the sign of the gravity head term in Eq. (14.2-43)).

\(P_{\text{vi}}\) = artificial viscous pressure for stabilizing test problems involving shock wave propagation and shock reflection from a rigid boundary. Not necessary for regular cavity blowdown problems.

If the net free fission-gas mass flux into a numerical node is negative (i.e., for net outflow), then \(P_{\text{vi}} = 0\).

If the net convective free fission-gas mass flux into a numerical cell is positive [14-27]:

(14.2-45)\[ P_{\text{vi}} = \frac{\text{C2VIPR} \cdot 0.5 \cdot \left( {p'}_{\text{fu,K}} + {p'}_{\text{fi,K}} \right) \cdot \left( u_{\text{fuca,K+1}} - u_{\text{fica,K}} \right)^{2}}{\theta_{\text{ficaxx,K}}}\]

where

\(K\) = index of the axial cavity node for which \(P_{\text{vi}}\) is being evaluated

\(\text{C2VIPR}\) = input constant which determines the magnitude of the numerical damping.

(14.2-46)\[\begin{split} \theta_{\text{ficaxx}} = \begin{cases} \theta_{\text{fica}} \text{ for } \theta_{\text{fica}} > \theta_{\text{ca}} \cdot \text{C1VIPR} \\ \theta_{\text{ca}} - \text{C1VIPR} \text{ for } \theta_{\text{fica}} < \theta_{\text{ca}} \cdot \text{C1VIPR} \\ \end{cases}\end{split}\]

where

\(\text{C1VIPR}\) = Input constant

The Moody friction factor \(F_{\text{friction}}\) in Eq. (14.2-44) depends on the Reynolds number

(14.2-47)\[ \text{Re}_{\text{pi}} = \frac{\left| u_{\text{fuca}} \right| D_{\text{ca}} \cdot \left( {\rho'}_{\text{fuca}} + {\rho'}_{\text{fica}} \right)}{\left( \theta_{\text{cs}} \cdot \text{VIFULQ} \right)}\]

where VIFULQ is the viscosity of liquid fuel which is input. The friction factor is

(14.2-48)\[\begin{split} F_{\text{friction}} = \begin{cases} \frac{64}{\text{Re}_{\text{pi}}} & \text{for } \text{Re}_{\text{pi}} \text{ CIREFU} \\ \text{CIFRFU} & \text{for } \text{Re}_{\text{pi}} \text{ CIREFU} \\ \end{cases}\end{split}\]

where CIREFU and CIFRFU are both input and should be made consistent in order to avoid a jump in the friction factor at \(\text{Re}_{\text{pi}} = \text{CIREFU}\).

The last term in Eq. (14.2-44) is necessary because the total momentum in the cell decreases due to ejection and this has to be considered in a momentum equation written in conservative form. There is no term accounting for the fuel melt-in because this fuel is added to the cavity with zero axial velocity, and therefore does not change the total momentum. However, since the generalized fuel smear density will change in a cell with melt-in, this will lead to a velocity decrease in such a cell.

14.2.7. Finite Difference Equations for the In-pin Motion

In the overview of the numerical scheme given in Section 14.2.4, it was pointed out that full donor cell spatial differencing and a largely explicit time differencing are used for treating the in-pin motion. The implicit aspect of the solution is that the mass and energy conservation equations are solved first and then a pressure is calculated on the basis of the mass and energy equation results. This advanced pressure is used in the momentum conservation equation.

The finite differencing of all the mass conservation equations is the same. The fuel mass conservation is used as an illustration.

(14.2-49)\[ \frac{\left( {\rho'}_{\text{fuca,K}}^{n + 1} - {\rho'}_{\text{fuca,K}}^{n} \right)}{\Delta t_{\text{PL}}} = \ - \frac{\left( \left( {\rho'} u \right)_{\text{fuca,K+1}} - \left( {\rho'} u \right)_{\text{fuca,K}} \right)}{\Delta z_{\text{K}}} + \sum_{\text{k}}{{S'}_{\text{K,k}}}\]

where

(14.2-50)\[\begin{split} \left( {\rho'} u \right)_{\text{fuca,K}} = \begin{cases} {\rho'}_{\text{fuca,K-1}} u_{\text{K}} & \text{for } u_{\text{K}} > 0 \\ {\rho'}_{\text{fuca,K}} u_{\text{K}} & \text{for } u_{\text{K}} < 0 \\ \end{cases}\end{split}\]

\(u_{\text{K}}\) = fuel velocity at the mesh cell boundary \(K\).

\({\rho'}_{\text{fuca,K-1}}\) = generalized fuel smear density at the mesh cell midpoint below boundary \(K\)

\({\rho'}_{\text{fuca,K}}\) = generalized fuel smear density at the mesh cell midpoint above boundary \(K\)

The numerical grid used in the program was discussed in Section 14.2.4, which gives an overview of the numerical scheme. Densities are at the cell centers and velocities at the cell edges (see schematic before the momentum conservation Eq. (14.2-61)). The source and sink terms have already been described in their finite difference form in the previous section.

The convective fluxes at the lower and upper boundaries of the cavity that are located in the end cells KK1 and KKMX, respectively, are

(14.2-51)\[ \left( {\rho'} u \right)_{\text{fuca,KK1}} = 0\]

and

(14.2-52)\[ \left( {\rho'} u \right)_{\text{fuca,KKMX+1}} = 0\]

The end cells are not always the same during a PLUTO2 run because the molten cavity can extend axially. When a new cell is added to the cavity, mass can only flow into this end cell if its cross section is at least 20% of that of the neighboring cell in the molten cavity. This had to be done because of problems with overcompression of cells with a very small cross section.

The finite difference form of the fuel energy Eq. (14.2-29) is:

(14.2-53)\[\begin{split}\frac{{\rho'}_{\text{fuca,K}} \left( e_{\text{fuca,K}}^{n + 1} - e_{\text{fuca,K}}^{n} \right)}{\Delta t_{\text{PL}}} = - \left\lbrack \left( {\rho'}_{\text{fuca}} e_{\text{fuca}} u_{\text{fuca}} \right)_{\text{K+1}}^{n} \right. \\ \left. - \left( {\rho'}_{\text{fuca}} e_{\text{fuca}} u_{\text{fuca}} \right)_{\text{K}}^{n} \right\rbrack \big/ \Delta z_{\text{K}} + e_{\text{fuca,K}}^{n} \left\lbrack \left( {\rho'}_{\text{fuca}} u_{\text{fuca}} \right)_{\text{K+1}}^{n} \right. \\ \left. - \left( {\rho'}_{\text{fuca}} u_{\text{fuca}} \right)_{\text{K}}^{n} \right\rbrack \big/ \Delta z_{\text{K}} + {S'}_{\text{fuca,me,K}}^{n} \left( e_{\text{fu,cabd,K}}^{n} - e_{\text{fuca,K}}^{n} \right) \\ + Q_{\text{K}}^{n} {\rho'}_{\text{fuca,K}}^{n} - h_{\text{fuca,cabd,K}}^{n} \left( T_{\text{fuca,K}}^{n} - T_{\text{fu,cabd,K}}^{n} \right) \pi D_{\text{ca,K}}^{n} \frac{\text{NRPI} \cdot \text{FNPI}}{\text{AXMX}} \\\end{split}\]

The fuel cavity temperature \(T_{\text{fuca}}\) in the above equation has to be calculated from the internal energy:

(14.2-54)\[\begin{split} & \text{For } e_{\text{fu,sol}} < e_{\text{fuca}} < e_{\text{fu,liq}}~ , \\ & T_{\text{fuca}} = T_{\text{fu,sol}} + \left( T_{\text{fu,liq}} - T_{\text{fu,sol}} \right) \cdot \frac{\left( e_{\text{fuca}} - e_{\text{fu,sol}} \right)}{\left( e_{\text{fu,liq}} - e_{\text{fu,sol}} \right)}\end{split}\]

(14.2-55)\[\begin{split} & \text{For } e_{\text{fuca}} > e_{\text{fu,liq}}~ , \\ & T_{\text{fuca}} = T_{\text{fu,liq}} + \frac{\left( e_{\text{fuca}} - e_{\text{fu,liq}} \right)}{C_{\text{p,fu}}}\end{split}\]

where \(C_{\text{p,fu}}\) is the fuel specific heat which is the single input value CPFU. The convective energy flux at cell boundary \(K\) in Eq. (14.2-53) in calculated as:

(14.2-56)\[\begin{split} \left( {\rho'}_{\text{fuca}} e_{\text{fuca}} u_{\text{fuca}} \right)_{\text{k}} = \begin{cases} \left( {\rho'}_{\text{fuca}} e_{\text{fuca}} \right)_{\text{K-1}} u_{\text{fuca,K}} \text{for } u_{\text{fuca,K}} > 0 \\ \left( {\rho'}_{\text{fuca}} e_{\text{fuca}} \right)_{\text{K}} u_{\text{fuca,K}} \text{for } u_{\text{fuca,K}} < 0 \\ \end{cases}\end{split}\]

At the lower and upper cavity ends that are in cells \(\text{KK1}\) and \(\text{KKMX}\), the convective energy fluxes are zero.

(14.2-57)\[ \left( {\rho'}_{\text{fuca}} e_{\text{fuca}} u_{\text{fuca}} \right)_{\text{KK1}}^{n} = 0\]

and

(14.2-58)\[ \left( {\rho'}_{\text{fuca}} e_{\text{fuca}} u_{\text{fuca}} \right)_{\text{KKMX+1}}^{n} = 0\]

By using the convective fluxes from Eq. (14.2-50) and Eq. (14.2-56), and the definitions of the energy gain and loss terms given earlier, and by differencing the second term of Eq. (14.2-53) like the first, Eq. (14.2-53) can be solved for \(e_{\text{fuca,K}}^{n + 1}\). Fuel temperatures that are shown in the PLUTO2 output are calculated by using Eq. (14.2-54) and Eq. (14.2-55).

For the finite difference form of the momentum equation the following quantities have to be defined at the edges of the numerical cells: the combined fuel/fission-gas generalized smear density and the cavity volume fraction. These quantities become:

(14.2-59)\[ {\rho'}_{\text{fufi,bk}} = 0.5 \left( {\rho'}_{\text{fuca,K-1}} + {\rho'}_{\text{fuca,K}} \right) + 0.5 \left( {\rho'}_{\text{fica,K-1}} + {\rho'}_{\text{fica,K}} \right)\]

(14.2-60)\[ \theta_{\text{ca,bk}} = 0.5 \left( \theta_{\text{ca,K}} + \theta_{\text{ca,K-1}} \right)\]

where the subscript \(bk\) indicates that these quantities are at the lower boundaries of cell \(K\). This is shown on the schematic below. On the numerical grid the velocities are also defined on the cell boundaries, whereas the pressures, densities and volume fractions are defined at the cell centers. This is also shown in the following schematic.

\(\theta_{\text{bk}}\)	\(\theta_{\text{bk+1}}\)
\({\rho'}_{\text{bk}}\)	\(\rho_{\text{bk+1}}\)
\(u_{\text{K}}\)	\(u_{\text{K+1}}\)
\(\theta_{\text{K-1}}\)	\(\theta_{\text{K}}\)	\(\theta_{\text{K+1}}\)

\(\rho_{\text{K-1}}\)	\(\rho_{\text{K}}\)	\(\rho_{\text{K+1}}\)
\(P_{\text{K-1}}\)	\(P_{\text{K}}\)	\(P_{\text{K+1}}\)
\(S_{\text{K-1}}\)	\(S'_{\text{K}}\)	\(S'_{\text{K+1}}\)

\(z_{\text{K}}\)

\(z_{\text{K+1}}\)

The finite difference form of the momentum conservation Eq. (14.2-44), is written using the definitions 14.2-46 and 14.2-47 as:

(14.2-61)\[\begin{split} \frac{\left( {\rho'}_{\text{fufi,bk}}^{n + 1} u_{\text{fuca,K}}^{n + 1} - {\rho'}_{\text{fufi,bk}}^{n} u_{\text{fuca,K}}^{n} \right)}{\Delta t_{\text{PL}}} = - \left\lbrack \left( u_{\text{fuca}}^{2} {\rho'}_{\text{fufi}} \right)_{\text{K}}^{n} \right. \\ \left. - \left( u_{\text{fuca}}^{2} {\rho'}_{\text{fufi}} \right)_{\text{K-1}}^{n} \right\rbrack \big/ \Delta z - \theta_{\text{ca,bk}} \left\lbrack \left( 1 - \varepsilon \right) \cdot \left( P_{\text{ca,K}}^{n} - P_{\text{ca,K-1}}^{n} \right) \right. \\ \left. + \varepsilon \cdot \left( P_{\text{ca,K}}^{n + 1} - P_{\text{ca,K-1}}^{n + 1} \right) + \left( P_{\text{vi,K}}^{n} - P_{\text{vi,K-1}}^{n} \right) \right\rbrack \big/ \Delta z - g {\rho'}_{\text{fufi,bk}} \\ - u_{\text{fuca,K}}^{n + 1} \left| u_{\text{fuca,K}}^{n} \right| {\rho'}_{\text{fufi,bk}}^{n} F_{\text{friction,bk}} \big/ \left( 2D_{\text{ca}} \right) - \left( {S'}_{\text{fuca,ej,K-1}}^{n + 1/2} \right. \\ \left. + {S'}_{\text{fuca,ej,K}}^{n + 1/2} + {S'}_{\text{fica,ej,K-1}}^{n + 1/2} + {S'}_{\text{fica,ej,K}}^{n + 1/2} \right) \cdot \left( u_{\text{fuca,K}}^{n + 1} + u_{\text{fuca,K}}^{n} \right) \cdot 0.25\end{split}\]

where

\(\varepsilon\) = Input value EPCH that can be between zero and one (see Eq. (14.2-1)),

and \(\Delta z\) implies \(0.5 \left( \Delta z_{\text{K-1}} + \Delta z_{\text{K}} \right)\).

By defining

(14.2-62)\[ {S'}_{\text{fuca,ej,bk}}^{n + 1/2} = \left( {S'}_{\text{fica,ej,K-1}}^{n + 1/2} + {S'}_{\text{fica,ej,K}}^{n + 1/2} + {S'}_{\text{fica,ej,K-1}}^{n + 1/2} + {S'}_{\text{fica,ej,K}}^{n + 1/2} \right) \cdot 0.5\]

and by collecting all terms with \(u_{\text{uica}}^{n + 1}\) on the left-hand side of the equation, one obtains

(14.2-63)\[\begin{split} u_{\text{fuca,K}}^{n + 1} \left\lbrack \frac{{\rho'}_{\text{fufi,bk}}^{n + 1}}{\Delta t_{\text{PL}}} + \left| u_{\text{fuca,K}}^{n} \right| {\rho'}_{\text{fufi,bk}}^{n} \frac{F_{\text{friction,bk}}}{\left( 2D_{\text{ca}} \right)} \right. \\ \left. + {S'}_{\text{fufi,ej,bk}}^{n + 1/2} \cdot 0.5 \right\rbrack = \frac{{\rho'}_{\text{fufi,bk}}^{n} u_{\text{fuca,K}}^{n}}{\Delta t_{\text{PL}}} \\ - \frac{\left\lbrack \left( u_{\text{fuca}}^{2} {\rho'}_{\text{fufi}} \right)_{\text{K}}^{n} - \left( u_{\text{fuca}}^{2} {\rho'}_{\text{fufi}} \right)_{\text{K-1}}^{n} \right\rbrack}{\Delta z} \\ - \theta_{\text{ca,bk}} \left\lbrack \left( 1 - \varepsilon \right) \cdot \left( P_{\text{ca,K}}^{n} - P_{\text{ca,K-1}}^{n} \right) \right. \\ \left. + \varepsilon \left( P_{\text{ca,K}}^{n + 1} - P_{\text{ca,K-1}}^{n + 1} \right) + \left( P_{\text{vi,K}}^{n} - P_{\text{vi,K-1}}^{n} \right) \right\rbrack \big/ \Delta z - g {\rho'}_{\text{fufi,bk}} \\ - {S'}_{\text{fuca,ej,bk}}^{n + 1/2} u_{\text{fuca,K}}^{n} \cdot 0.5 \\\end{split}\]

The convective momentum flux in Eq. (14.2-63) is calculated as

(14.2-64)\[\begin{split} \left( u_{\text{fuca}}^{2} {\rho'}_{\text{fufi}} \right)_{\text{K}} = \begin{cases} {\rho'}_{\text{fufi,K}} u_{\text{fuca,K}}^{2} & \text{if } \left( u_{\text{fuca,K}} + u_{\text{fuca,K+1}} \right) > 0 \\ {\rho'}_{\text{fufi,K}} u_{\text{fuca,K+1}}^{2} & \text{if } \left( u_{\text{fuca,K}} + u_{\text{fuca,K+1}} \right) < 0 \end{cases}\end{split}\]

(14.2-65)\[\begin{split} \left( u_{\text{fuca}}^{2} {\rho'}_{\text{fufi}} \right)_{\text{K-1}} = \begin{cases} {\rho'}_{\text{fufi,K-1}} u_{\text{fuca,K-1}}^{2} & \text{if } \left( u_{\text{fuca,K-1}} + u_{\text{fuca,K}} \right) > 0 \\ {\rho'}_{\text{fufi,K-1}} u_{\text{fuca,K}}^{2} & \text{if } \left( u_{\text{fuca,K-1}} + u_{\text{fuca,K}} \right) < 0 \end{cases}\end{split}\]

where

(14.2-66)\[ {\rho'}_{\text{fufi,K}} = {\rho'}_{\text{fuca,K}} + {\rho'}_{\text{fica,K}}\]

The momentum fluxes for the lower and upper end cells of the cavity, which are designated by KK1 and KKMX, are:

(14.2-67)\[\begin{split} \left( u_{\text{fuca}}^{2} {\rho'}_{\text{fufi}} \right)_{\text{KK1}} = \begin{cases} {\rho'}_{\text{fufi,KK1}} u_{\text{fuca,KK1+1}}^{2} \cdot 0.25 & \text{if } u_{\text{fuca,KK1+1}} > 0 \\ {\rho'}_{\text{fufi,KK1}} u_{\text{fuca,KK+1}}^{2} & \text{if } u_{\text{fuca,KK1+1}} < 0 \end{cases}\end{split}\]

(14.2-68)\[\begin{split} \left( u_{\text{fuca}}^{2} {\rho'}_{\text{fufi}} \right)_{\text{KKMX}} = \begin{cases} \rho_{\text{fufi,KKMX}} u_{\text{fuca,KKMX}}^{2} & \text{if } u_{\text{fuca,KKMX}} > 0 \\ \rho_{\text{fufi,KKMX}} u_{\text{fuca,KKMX}}^{2} \cdot 0.25 & \text{if } u_{\text{fuca,KKMX}} < 0 \end{cases}\end{split}\]

The factor 0.25 in the above convection terms comes from the assumption of a zero velocity at the end of the cavity.

The momentum Eq. (14.2-63) can be solved for \(u_{\text{fuca,K}}^{n + 1}\) if Eq. (14.2-59), Eq. (14.2-60), and Eq. (14.2-64) through Eq. (14.2-68) are used.

14.2.8. Time-step Determination for the In-Pin Motion

The PLUTO2 time step \(\Delta t_{\text{PL}}\) used in the numerical solution of all the in-pin and channel conservation equations is restricted by the sonic Courant conditions for both the in-pin and channel flows. The sonic Courant condition for the channel flow and the determination of the PLUTO2 time step \(\Delta t_{\text{PL}}\) is given at the end of the channel flow description in Section 14.4.6.4. In the present section, only the restriction imposed by the sonic Courant condition for the in-pin flow is described.

The time-step size for the in-pin motion is computed to be a fraction, 0.4, of the minimum time step based on the sonic Courant condition

(14.2-69)\[ \Delta t_{\text{PL,pin}} = 0.4 \cdot \min\left\lbrack \frac{{z}_{\text{K}}}{v_{\text{sonic,K}} + |u_{\text{fuca,K}}|} \right\rbrack_{\text{K = KK1,KKMX}}\]

The minimum in Eq. (14.2-69) is evaluated over all the axial cells of the molten fuel cavity. The sonic velocity is calculated from an expression for an adiabatic, homogeneous two-component gas-liquid mixture which is based on Eq. 27 in Reference [14-28].

(14.2-70)\[\begin{split} v_{\text{sonic}}^{2} = \gamma_{\text{fi}} P_{\text{fica}} \big/ \left\{ \left\lbrack \alpha_{\text{fica}}^{2} \cdot \rho_{\text{fica}} + \alpha_{\text{fica}} \left( 1 - \alpha_{\text{fica}} \right) \rho_{\text{fuca}} \right\rbrack \right. \\ \left. + \left\lbrack \left( 1 - \alpha_{\text{fica}} \right)^{2} \rho_{\text{fica}} + \alpha_{\text{fica}} \left( 1 - \alpha_{\text{fica}} \right) \rho_{\text{fica}} \right\rbrack \gamma_{\text{fi}} P_{\text{fica}} K_{\text{fu}} \right\} \\\end{split}\]

where

\(\alpha_{\text{fica}} = \frac{\theta_{\text{fica}}}{\theta_{\text{ca}}}\) = void fraction in the cavity

\(\gamma_{\text{fi}} = \frac{C_{\text{p,fi}}}{C_{\text{v,fi}}} = 1.4\) (value assumed in PLUTO2)

\(K_{\text{fu}} = \text{CMFU}\) = input liquid fuel compressibility

The above equation holds for adiabatic gas behavior, although the in-pin fission-gas treatment in \(\text{PLUTO2}\) is isothermal (the gas temperature is assumed to be always equal to the fuel temperature). However, the sonic velocity for adiabatic gas behavior is higher than that for isothermal gas behavior, and thus, leads to a more conservative (i.e., smaller) time step. Moreover, if a pure gas flow were treated in sections of pins with a prefabricated central hole, the current time-step determination would actually be necessary.