14.5. Temperature Calculation of Cladding, Structure, Reflector and Liquid Sodium Slugs

14.5.1. Liquid Sodium, Cladding, structure, and Reflector Temperature Calculation Outside of the Interaction Region

The expulsion of coolant from the core after PLUTO2 initiation (due to fuel-coolant interaction) results in significant preheating of cladding and other structures prior to the passage of the void interface, especially for the lower liquid slug, which has a large axial thermal gradient. Consequently, it is necessary to continue to compute the temperatures outside of the interaction zone after PLUTO2 initiation in order to provide accurate updated initial temperatures for cells being added t the integration zone (i.e., voided region). Core cladding temperatures outside of the interaction zone are computed in PLHTR, which is a modified version of the standard SAS [in heat-transfer model TSHTRV. Special routines were developed to compute the liquid coolant, structure, plenum cladding, and reflector temperatures outside of the interaction zone; a description of these subroutines follows.

Coolant temperatures are computed (in subroutine PLCOOL) based on a heat-transfer time step, as are those of the wetted structure, cladding, and reflector. The heat-transfer time step may be altered (in PLUDRV) to satisfy a Courant condition in either slug, based on the instantaneous sodium velocity.

The PLUTO coolant nodes, unlike those in the SAS boiling model, are centered in the numerical cell in order to be consistent with the PLUTO node structure in the interaction zone. The finite-difference equation, given below, is time explicit and uses donor cell differencing for the convective term:

(14.5-1)\[ A_{\text{ch}} \rho_{\text{N1}} C_{\text{p,N1}} L_{\text{i}} \left( T_{\text{N1,i}}^{n + 1} - T_{\text{N1}}^{n} \right) \ + \Delta M_{\text{N1,i}} C_{\text{p,N1}} \left( T_{\text{N1,i}}^{n} - T_{\text{N1,i-1}}^{n} \right) = H_{\text{i}}^{l} L_{\text{i}} \Delta t_{\text{Ht}}~, \text{ for } W_{\text{N1}} > 0\]

where

\(A_{\text{ch,i}}\) = local flow area,

\(L_{\text{i}}\) = wetted length in axial cell \(i\),

\(T_{\text{N1,i}}^{n}\); \(T_{\text{N1,i}}^{n + 1}\) = nodal coolant temperatures at times \(t\) and \(t + \Delta t\).

\(\Delta M_{\text{N1,i}}\) = mass transport into axial cell \(I\) during time interval \(\Delta t\).

\(H_{\text{i}}^{l}\) = heat-transfer rate from cladding and structure per unit length.

\(\rho_{\text{N1}}\) = coolant density.

\(C_{\text{p,N1}}\) = coolant specific heat.

\(\Delta t_{\text{Ht}}\) = heat-transfer time step.

\(W_{\text{N1}}\) = liquid sodium mass flowrate.

A similar equation is used for the case of downflow.

Normally \(L_{\text{i}}\) is set equal to the cell length:

(14.5-2)\[ L_{\text{i}} = z_{\text{i+1}} - z_{\text{i}}\]

where \(z_{\text{i}}\) is the elevation of the lower cell boundary. Also, the mass transport \(\Delta M_{\text{i}}\) is usually taken to be the product of the mean flowrate \(W_{\text{N1}}\), computed from the interface displacement, times \(\Delta t_{\text{Ht}}\). Exceptions are made for cells containing the void interfaces.

Consider the mesh cell containing the upper interface of the lower slug. For this case the wetted length is given by

(14.5-3)\[ L_{\text{i}} = z_{\text{if}}^{n + 1} - z_{\text{i}}\]

where \(z_{\text{if}}^{n + 1}\) = interface elevation for the lower slug at the end of the heat-transfer time step and \(z_{\text{i}}\) = location of the fixed mesh cell boundary below the slug interface. For the case of expulsion (negative velocity in the lower slug), the inflow into the end cell is zero unless the interface crossed the upper boundary:

(14.5-4)\[\begin{split} \Delta M_{\text{N1,i}} = \begin{cases} 0 & \text{for } z_{\text{if}}^{n} < Z_{\text{i+1}} \\ - A_{\text{ch,i}} \left( 1 - f \right) \rho_{\text{N1,i}} \left( z_{\text{if}}^{n + 1} - z_{\text{i+1}} \right) & \text{for } z_{\text{if}}^{n} \geq z_{\text{i+1}} \\ \end{cases}\end{split}\]

where

\(f\) = input volume fraction CINAFO of liquid film left behind.

\(z_{\text{if}}^{n}\) = interface elevation for lower slug at time \(t\).

For the case when the lower slug first reenters a cell, the coolant temperature for the end cell is set by \(T_{\text{ch,i}}^{n + 1} = T_{\text{ch,i-1}}^{n + 1}\). In subsequent time steps, the end node temperature (for reentry or \(W_{\text{N1}} > 0\)) is computed with the reduced wetted length and with \(\Delta M_{\text{i}} = W_{\text{N1}} \Delta t_{\text{Ht}}\). Similar reasoning is applied to the treatment of the segment containing the lower interface of the upper slug.

The reflector, gas plenum cladding, and structure temperatures outside of the interaction zone are computed in subroutine FLSTR using straightforward, explicit-time-differenced equations. Like the coolant calculation, these temperatures are computed every heat-transfer time step. The difference equations are based on the same nodal structure as used in the pre-PLUTO2 SAS4A calculations and used the same FORTRAN variable names, which eliminates the need to initialize these variables when PLUTO2 calculations are begun. Reinitialization is required, however, during coolant reentry.

14.5.2. Cladding and Reflector Temperature Calculation in the Interaction Region

The transient cladding, reflector, and structure temperatures within the interaction region are computed in subroutine PLTECS, which is called form subroutine PLUDRV every PLUTO time step (see Figure 14.5.1). In the interaction region, both the cladding and reflector have three radial nodes (per axial segment), each of which has a different FORTRAN name. However, a temporary radial temperature array is defined with the numbering scheme shown in Figure 14.5.1 for the purpose of facilitating the solution of the radial heat conduction problem.

To evaluate cladding temperatures more accurately, one desires a constantly updated fuel surface temperature (every PLUTO2 time step) rather than the one computed from PLHTR every heat-transfer time step. This updated fuel surface temperature is obtained by extending the nodal structure to overlap that of the fuel model as shown in Figure 14.5.1. By overlapping, the fuel surface temperature is computed along with the cladding temperatures every PLUTO2 time step. To insure consistency with the fuel model, the temperature of node 2 (fuel surface) is reset along with that of node 1 every heat-transfer time step. The fuel temperature calculation in PLHTR, in turn, uses an integrated fuel-heat-loss boundary condition obtained from the cladding model.

The transient heat-transfer equation for each node is expressed in the following standard form:

(14.5-5)\[ \left( \text{MC}_{\text{p}} \right)_{\text{i}} \frac{\text{dT}_{\text{i}}}{\text{dt}} \ = \left( ha \right)_{\text{i-1}} \left( T_{\text{i-1}} - T_{\text{i}} \right) \ + \left( ha \right)_{\text{i}} \left( T_{\text{i+1}} - T_{\text{i}} \right) + Q_{\text{i}}^{l}\]

where

\(T_{\text{i}}\) is the nodal temperature.

\(\left( \text{MC}_{\text{p}} \right)_{\text{i}}\) is the heat capacity of the control volume per unit length.

\(\left( ha \right)_{\text{i}}\) is the coefficient of heat transfer from node \(I\) to \(I + 1\) per unit length,

\(Q_{\text{i}}^{l}\) is the control volume heat-generation rate per unit length.

The coefficients \(\left(\text{MC}_{\text{p}} \right)_{\text{i}}\) and \(\left( ha \right)_{\text{i}}\) are evaluated by the following relations:

(14.5-6)\[ \left( \text{MC}_{\text{p}} \right)_{\text{i}} = \pi \left( r_{\text{i}}^{2} \ - {\hat{r}}_{\text{i-1}}^{2} \right) \rho_{\text{i+1}} C_{\text{p,i-1}} \ + \pi \left( {\hat{r}}_{\text{i}}^{2} - r_{\text{i}}^{2} \right) \rho_{\text{i}} C_{\text{p,i}}\]

(14.5-7)\[ \left( ha \right)_{\text{i}} = \frac{2\pi r_{\text{i}} {\hat{k}}_{\text{i}}}{\left( r_{\text{i+1}} \ - r_{\text{i}} \right)}~, \text{ for } i \neq 2,5\]

(14.5-8)\[ \left( ha \right)_{\text{i}} = 2\pi r_{\text{i}} {\hat{h}}_{\text{i}}~, \text{ for } i = 2,5\]

where \(\rho_{\text{i}}\), \(C_{\text{p,i}}\), and \(k_{\text{i}}\) are the density, specific heat, and thermal conductivity of the material between nodes \(i\) and \(i+1\). Based on the numbering scheme shown in Figure 14.5.1, the quantities \(k_{3}\) and \(k_{4}\) are set equal to the input value of the cladding thermal conductivity DCL. The products \(\rho_{3} C_{\text{p,4}}\) and \(\rho_{4} C_{\text{p,4}}\) are set equal to the input parameter CPCLRH. The mean radius \({\hat{r}}_{\text{i}}\) is defined by

(14.5-9)\[ {\hat{r}}_{\text{i}} = 1/2 \left( r_{\text{i}} + r_{\text{i+1}} \right)\]

where \(r_{\text{i}}\) is the radius of node \(i\).

Cladding melting is accounted for by using an augmented clad heat capacity, \({C'}_{\text{p}}\), when the clad temperature falls in the melting band, where \({C'}_{\text{p}}\) is defined by:

(14.5-10)\[ {C'}_{\text{p}} = C_{\text{p}} + \frac{\lambda}{\Delta T_{\text{me}}}\]

where

\(C_{\text{p}}\) = is the normal specific heat of the solid cladding given by the input parameter CPCL.

\(\lambda\) = is the latent heat of fusion which is evaluated as the difference between the input values of energies of cladding at liquidus and solidus, EGSELQ and EGSESO.

\(\Delta T_{\text{mc}}\) = is the difference in the liquidus and solidus temperatures of the cladding which are input (see TESELQ and TESESO, respectively).

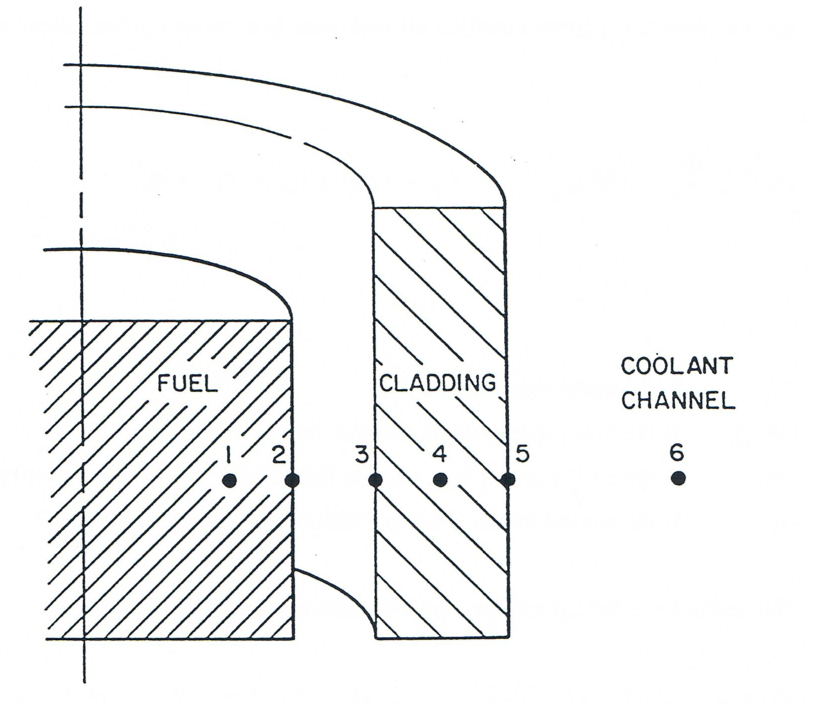
Figure 14.5.1 Radial Node Numbering Scheme Used in Subroutine PLTECS for the Temperature Calculation of Cladding and Reflector in the Interaction Region

When entering or leaving the melting band, an adjustment o the computed temperature is required to insure that energy is properly conserved in the system. The specific heat of the cladding above the liquidus temperature is given by the input value CPSE.

The coefficient of heat transfer \(h_{2}\) is set equal to the gap coefficient in the active fuel and blanket regions. In the plenum and reflector regions, however, \(h_{2}\) is set equal to zero to simulate an adiabatic boundary condition at the inner cladding surface. The form of the equations for \(\left( \text{MC}_{\text{p}} \right)_{\text{i}}\) and \(\left( ha \right)_{\text{i}}\), for the reflector region is slightly modified to correspond to a slab geometry, rather than a cylindrical one.

The heat-transfer coefficient \(\left( ha \right)\), and effective sink temperature \(T_{6}\) for the outer surface of the cladding and reflector are given by:

(14.5-11)\[ \left( ha \right)_{5} = \left( ha \right)_{\text{Na,cl}} + \left( ha \right)_{\text{fu,cl}} + \left( ha \right)_{\text{ff,cl}}\]

(14.5-12)\[ \left( ha \right)_{5} = \left( ha \right)_{\text{Na,cl}} + \left( ha \right)_{\text{fu,cl}} + \left( ha \right)_{\text{ff,cl}}\]

The three terms on the right-hand side of these equations account for heat transfer from the cladding (or structure) to each component in the channel: namely, sodium (and fission gases), moving fuel, and stationary frozen fuel.

Eq. (14.5-12) is converted to a fully implicit difference equation in time. This scheme was used to obtain numerical stability when analyzing thin cladding without using excessively small PLUTO time increments. This feature will be especially useful in the analysis of ablating clad where the nodal heat capacities are shrinking to zero. The resulting difference equations for each axial slice of the core are a set of simultaneous equations for the nodal temperatures, which are solved by the Thomas algorithm for tri-diagonal coefficient matrices.

14.5.3. Structure Temperature Calculation in the Interaction Region

The temperature calculation in the subassembly hexcan wall or in the flow tube of an experiment test section normally uses the same two-node mesh structure as the remainder of the SAS4A code. However, when the SAS4A input specifies one large and one rather small node width (\(w_{\text{small}} < 0.1 w_{\text{sr}}\)), the width of the small node is set to \(w_{\text{small}} = 0.1 w_{\text{sr}}\). This is done in order to avoid stability problems in the explicit temperature calculation performed in PLUTO2 or in LEVITATE. As for the pre-failure calculation of the SAS node, it is recommended that the structure node facing the coolant channel should be considerable thinner than that for the structure node facing the intersubassembly gap. This is because the node facing the coolant channel should be capable of rapidly responding to changes in the transfer from coolant or molten fuel.

In order to treat the heat transfer between two unequal nodes accurately, an approach is used in which the temperature profile in the structure is approximated by a parabola rather than a straight line between the two temperature nodes. This approach, which was originally developed for LEVITATE, has been adopted in PLUTO2. It is described in detail in Section 16.5.7.2.