16.3. Fuel Ejection from the Pins and Fuel-pin Disruption

The hydrodynamic in-pin model is connected to the channel model via the mechanisms of molten fuel ejection into the channel and fuel-pin disruption. The models describing these processes are described below.

16.3.1. Fuel Ejection via a Cladding Rupture

The molten fuel/fission-gas mixture can be ejected from the pin cavity into the channel in any axial cell where a cladding rupture has already occurred. The original cladding failure location is determined in the routines FAILUR and FUINIT, just before LEVITATE is initiated. Once control passes to LEVITATE, additional nodes can fail, leading to the increase of the original failure and, occasionally, the initiation of new failures. Thus, two or more disjoint failures can be present in a channel under certain circumstances. The fuel-pin rip enlargement is performed in the routine LEIF.

The stress in the cladding in the axial cell is calculated as follows:

(16.3-1)\[ \sigma_{\text{cl,i}} = \frac{P_{\text{ca,k}} \cdot R_{\text{ca,k}} - P_{\text{cl,i}} \cdot R_{\text{cl,os,i}}}{\Delta R_{\text{cl,i}}}\]

The ultimate tensile strength for the cladding is calculated using the function \(\sigma_{\text{U}} \left( T \right)\) for each radial cladding node in the axial cell \(i\):

(16.3-2)\[ \sigma_{\text{cl,i}}^{U} = \frac{\sigma^{U}\left( T_{\text{cl,os,i}} \right) \cdot \left( R_{\text{cl,os,i}} \ - R_{\text{cl,in,i}} \right) + \sigma^{U}\left( T_{\text{cl,in,i}} \right) \cdot \left( R_{\text{cl,in,i}} \ - R_{\text{cl,is,i}} \right)}{\left( R_{\text{cl,os,i}} - R_{\text{cl,is,i}} \right)}\]

The rupture will be extended to cell \(i\) if:

(16.3-3)\[ \sigma_{\text{cl,i}} > \sigma_{\text{cl,i}}^{U}\]

during any time step. All the nodes in the LEVITATE region are scanned every cycle. Once the rupture has occurred in one axial node, that node will continuously be checked for fuel ejection in each cycle.

The ejection of the molten fuel from the pin cavity into the channel is performed in the LE1PIN routine. Only the nodes where the cladding has been ruptured can eject fuel. Ejection will occur in these nodes if:

(16.3-4)\[ P_{\text{ca,K}} > P_{\text{ch,i}}\]

and

(16.3-5)\[ \alpha_{\text{fu,ca,k}} = \frac{\theta_{\text{fu,ca,k}}}{\theta_{\text{ca,k}}} > 0.1\]

An additional constraint, designed to avoid numerical problems related to a fully incompressible channel configuration, is:

(16.3-6)\[ \frac{\left( \theta_{\text{ch,i}} - \theta_{\text{ch,op,i}} \right) + \theta_{\text{fu,i}} \ + \theta_{\text{se,i}} + \theta_{\text{fu,i}}}{\theta_{\text{ch,i}}} \leq 0.95\]

i.e., the volume fraction of the incompressible components (crust, fuel, steel, and chunks) should not be more than 95% of the original channel volume. If all the conditions 16.3-4 through 16.3-6 are satisfied, the injection calculation begins by calculating the in-pin pressure after injection. An estimate of the amounts of fuel that can be ejected during a typical LEVITATE time step indicated that at the time of failure, the limiting factor in the ejection process is the inertia for the molten fuel. For the time steps usually used in LEVITATE (approximately 2⨉10^-5 s) and the typical conditions for a loss-of-flow situation, where the coolant channel is voided, it was found that the pressure in the pin cavity will decrease initially by about 0.5% of the pressure difference between the cavity and the channel. However, the fuel in the cavity can be accelerated laterally quite rapidly, and the inertial constraint becomes insignificant within a few milliseconds of the failure time. Afterwards, the ejection process is rapid enough to equilibrate the pressures in the cavity and channel within one or two typical LEVITATE time steps.

(16.3-7)\[ P_{\text{ca,k}}^{n + 1} = P_{\text{ca,k}}^{n} - \left( P_{\text{ca,k}} \ - P_{\text{ch,i}} \right) \cdot \text{CIPINJ} \cdot \text{DTPLU}\]

The input constant CIPINJ has the recommended value \(2.5 \times 10^{4}\). For this value of CIPINJ, the product CIPINJ ⨉ DTPLU has the value 0.5 and the pressure difference between the cavity and the coolant channel will be equilibrated very rapidly. This model does not account for the inertial effects mentioned above, which are present for a short time after the failure has occurred. A more mechanistic model accounting for these effects is currently being developed. With the assumption that the fuel, fission gas and fuel vapor in the axial cell \(k\) are homogeneously mixed, we can now calculate the amount of fuel which has to be ejected from the cavity in order to establish the pressure \(P_{\text{ca,k}}^{n + 1}\):

(16.3-8)\[\begin{split} \Delta {\rho'}_{\text{fu,k}} = \left\{ \left\lbrack \theta_{\text{fi,ca,k}} - \theta_{\text{fu,ca,k}} \cdot \text{CMFU} \cdot \left( P_{\text{ca,k}} - P_{\text{fv,ca,k}} \right) \right\rbrack \cdot P_{\text{ca,k}} \right. \\ \left. + \left( R_{\text{fi}} \cdot {\rho'}_{\text{fi,ca}} + R_{\text{fv}} \cdot {\rho'}_{\text{fv,ca,k}} \right) \cdot T_{\text{fu,ca,k}} \right\} \cdot \rho_{\text{fu,ca,k}} \\ \div \left( P_{\text{ca,k}} + f_{\text{fi,fu,k}} \cdot R_{\text{fi}} \cdot T_{\text{fu,ca,k}} \cdot \rho_{\text{fu,ca,k}} \right. \\ \left. + f_{\text{fv,fu,k}} \cdot R_{\text{fv}} \cdot T_{\text{fu,ca,k}} \cdot \rho_{\text{fu,ca,k}} \right)\end{split}\]

where the input variable CMFU represents the compressibility of the molten fuel and

(16.3-9)\[ f_{\text{fi,fu,k}} = \frac{{\rho'}_{\text{fi,ca,k}}}{{\rho'}_{\text{fu,ca,k}}}\]

(16.3-10)\[ f_{\text{fi,fu,k}} = \frac{{\rho'}_{\text{fv,ca,k}}}{{\rho'}_{\text{fu,ca,k}}}\]

In the derivation of Eq. (16.3-8), we used the assumption that, for injection purposes, the fuel vapor behaves as a gas. Further fuel vaporization can take place in the next cycle. It should also be noted that \(\Delta {\rho'}_{\text{fu,k}}\) represents the change in the generalized density of the in-pin fuel. This change refers to the fuel in all the pins in the subassembly, as explained in the corresponding PLUTO2 section.

The amount of fission gas and fuel vapor ejected is then calculated as

(16.3-11)\[ \Delta {\rho'}_{\text{fi,k}} = f_{\text{fi,fu,k}} \cdot \Delta {\rho'}_{\text{fu,ca,k}}\]

(16.3-12)\[ \Delta {\rho'}_{\text{fv,k}} = f_{\text{fv,fu,k}} \cdot \Delta {\rho'}_{\text{fu,ca,k}}\]

The fuel vapor mass ejected is then added to the mass of the liquid fuel ejected. It is noteworthy that the fuel vapor pressure is used only for the momentum calculation in the pin and for the fuel ejection. No fuel vapor conservation equations are solved in the pin cavity.

The new channel partial pressures are then recalculated:

(16.3-13)\[ P_{\text{fv,i}} = \frac{R_{\text{fv}} \cdot {\rho'}_{\text{fv,i}} \cdot T_{\text{fv,i}}}{\theta_{\text{vg,i}}^{n + 1}}\]

(16.3-14)\[ P_{\text{sv,i}} = \frac{R_{\text{sv}} \cdot {\rho'}_{\text{sv,i}} \cdot T_{\text{sv,i}}}{\theta_{\text{vg,i}}^{n + 1}}\]

If \(\frac{\theta_{\text{Na,lq,i}}}{\theta_{\text{ch,op,i}}} \leq 0.3\)

(16.3-15)\[ P_{\text{fi,i}} = \frac{R_{\text{fi}} \cdot \left( {\rho'}_{\text{fi,i}} + \Delta {\rho'}_{\text{fi,k}} \right) \cdot T_{\text{fi,i}}}{\theta_{\text{vg,i}}^{n + 1}}\]

If \(\frac{\theta_{\text{Na,lq,i}}}{\theta_{\text{ch,op,i}}} > 0.3\), then

(16.3-16)\[ P_{\text{fi,i}} = \frac{- \theta_{\text{vg,i}}^{n + 1} + \sqrt{\left( \theta_{\text{vg,i}}^{n + 1} \right)^{2} + 4 \theta_{\text{Na,}l \text{q,i}} \cdot \text{CMNL} \cdot \left( {\rho'}_{\text{fi,i}} + \Delta {\rho'}_{\text{fi,ca,k}} \right) \cdot R_{\text{fi}} \cdot T_{\text{fi,i}} }}{2 \theta_{\text{Na,} l \text{q,i}} \cdot \text{CMNL}}\]

If \(\theta_{\text{Na},l \text{q}} = 0\), i.e., if the sodium present is in the form of single-phase vapor:

(16.3-17)\[ P_{\text{Na,i}} = \frac{R_{\text{Na}} \cdot {\rho'}_{\text{Na,i}} \cdot T_{\text{Na,i}}}{\theta_{\text{vg,i}}^{n + 1}}\]

If \(0 < \theta_{\text{Na}, l \text{q}}\), i.e., two-phase sodium is present:

(16.3-18)\[ P_{\text{Na,i}} = P_{\text{Na}}\left( T_{\text{Na,i}} \right)\]

where CMNL is the compressibility coefficient of the liquid sodium and \(\theta_{\text{vg,i}}^{n + 1}\) is:

(16.3-19)\[ \theta_{\text{vg,i}}^{n + 1} = \theta_{\text{vg,i}} - \frac{\Delta {\rho'}_{\text{fu,ca,k}}}{\rho_{\text{fu,k}}}\]

The new tentative channel pressure is:

(16.3-20)\[ P_{\text{ch,i}}^{n + 1} = P_{\text{Na,i}} + P_{\text{fi,i}} + P_{\text{sv,i}} + P_{\text{fv,i}}\]

If this pressure is below the pressure in the cavity after injection, i.e.,

(16.3-21)\[ P_{\text{ch,i}}^{n + 1} < P_{\text{ca,k}}^{n + 1}\]

then no further iterations are necessary and \(P_{\text{ch,i}}^{n + 1}\) remains the new pressure in the channel. If Eq. (16.3-21) is not satisfied, too much material was ejected from the cavity into the channel. A new pressure in the pin cavity is selected:

(16.3-22)\[ P_{\text{ca,k}}^{n + 1} = \left( P_{\text{ca,k}}^{n} + P_{\text{ca,k}}^{n + 1} \right) \cdot 0.5\]

and the procedure outlined in Eq. (16.3-7) through Eq. (16.3-20) is repeated until the condition in 16.3-18 is satisfied.

It should be noted that in Eq. (16.3-15), the fission-gas pressure is calculated by assuming that the fission gas injected has the same temperature as the fission gas in the channel. This is necessary because the fission gas and sodium have to be at the same temperature, which has already been calculated in the routine LENAEN. The additional energy carried by the injected fission gas, which in fact has the temperature \(T_{\text{fu,ca,k}}\) will be added to the fission gas/sodium mixture in the next cycle, when solving the energy equation for these components. Finally, the fuel and fission-gas densities in the pin and channel are updated.

(16.3-23)\[ {\rho'}_{\text{fu,ca,k}} = {\rho'}_{\text{fu,ca,k}} - \Delta{\rho'}_{\text{fu,ca,k}}\]

(16.3-24)\[ {\rho'}_{\text{fi,ca,k}} = {\rho'}_{\text{fi,ca,k}} - \Delta{\rho'}_{\text{fi,ca,k}}\]

(16.3-25)\[ {\rho'}_{\text{fu,i}} = {\rho'}_{\text{fu,i}} + \Delta{\rho'}_{\text{fu,ca,k}}\]

(16.3-26)\[ {\rho'}_{\text{fu,i}} = {\rho'}_{\text{fi,i}} + \Delta{\rho'}_{\text{fi,ca,k}}\]

In the Release 1.1 version of LEVITATE a mechanistic calculation of the in-pin fuel ejection has been added. This model can be used by setting the input variable INRAEJ=1. If INRAEJ=0 the ejection of the fuel into the channel is calculated as described above.

The mechanistic ejection model calculates the radial velocity of the in-pin molten fuel/gas mixture, \(u_{\text{ca-ch,k}}\), at each axial location where the cladding has been ruptured. This velocity is recalculated each time step. The amounts of fuel and fission gas ejected each time step are calculated as follows:

(16.3-27)\[ \Delta{\rho'}_{\text{fu,k}} = {\rho'}_{\text{fu,k}} \cdot \frac{V_{\text{fuel ejected}}}{V_{\text{fuel cavity}}} \ = {\rho'}_{\text{fu,k}} \cdot \frac{u_{\text{fu,ca-ch,k}} \cdot \Delta t}{\pi \cdot R_{\text{ca,k}}}\]

(16.3-28)\[ \Delta{\rho'}_{\text{fi,k}} = {\rho'}_{\text{fi,k}} \cdot \frac{u_{\text{fu,ca-ch,k}} \cdot \Delta t}{\pi \cdot R_{\text{ca,k}}}\]

(16.3-29)\[ \Delta {\rho'}_{\text{fv,k}} = {\rho'}_{\text{fv,k}} \cdot \frac{u_{\text{fu,ca-ch,k}} \cdot \Delta t}{\pi \cdot R_{\text{ca,k}}}\]

The pressure in the cavity is then calculated solving equation 16.3-8 for \(P_{\text{ca,k}}\) and the pressure in the coolant channel is calculated using Eq. (16.3-13) through Eq. (16.3-20). If

(16.3-30)\[ P_{\text{ch,i}}^{n + 1} < P_{\text{ca,k}}^{n + 1}\]

then no further iterations are necessary. If 16.3-23-4 is not satisfied then too much material was ejected from the cavity into the channel. The radial velocity is reduced:

(16.3-31)\[ u_{\text{fu,ca-ch,k}}^{n + 1} = u_{\text{fu,ca-ch,k}}^{n + 1} \cdot 0.5\]

and the procedure for pressure calculation is repeated.

The key element in the calculation described above is the radial fuel velocity \(u_{\text{fu,ca-ch,k}}\), which is calculated as described below.

The radial velocity calculation first updates all radial velocities considering only the radial acceleration \(a_{\text{fu,ca-ch,k}}\), and ignoring temporarily the axial transport of radial momentum:

(16.3-32)\[ u_{\text{fu,ca-ch,k}}^{n + 1} = u_{\text{fu,ca-ch,k}} + a_{\text{fu,ca-ch,k}} \cdot \Delta t\]

where \(a_{\text{fu,ca-ch,k}}\) is the radial acceleration of the molten fuel in the cavity in the axial cell \(k\). This acceleration is calculated using the simplified geometry illustrated in Figure 16.3.1. The pressure difference between the pin cavity and the coolant channel is assumed to act on the fuel contained in the shaded volume. The rip size is considered to be of the same order of magnitude as the cavity radius. The acceleration is calculated as follows:

(16.3-33)\[\begin{split} a_{\text{fu,ca-ch,k}} = \frac{\sum\text{Forces}}{\text{Mass}} = \frac{R_{\text{ca,k}} \cdot z_{\text{k}}}{0.9 \cdot R_{\text{ca,k}}^{z} \cdot z_{\text{k}} \cdot \rho_{\text{fu,k}}}\left\{ P_{\text{ca-ch,k}} - 0.5 \cdot \rho_{\text{fu,k}} \cdot u_{\text{fu,ca-ch,k}} \right. \\ \left. \cdot \left| u_{\text{fu,ca-ch,k}} \right| \cdot C_{\text{ORIFICE}} - C_{\text{SHEAR}} \cdot \eta_{\text{fu,k}} \cdot \frac{u_{\text{fu,ca-ch,k}}}{R_{\text{ca,k}}} \right\}\end{split}\]

where: \(\Delta P_{\text{ca-ch,k}} = P_{\text{ca,k}} - P_{\text{ch,i}}\)

\(C_{\text{ORFICE}}\) is an orifice coefficient used in the calculation of the flow pressure drop across the rip. This coefficient is currently zero in the code.

\(C_{\text{SHEAR}}\) is a coefficient associated with the shear forces exerted on the accelerating fuel. It can be determined from geometrical considerations. The current value is 6.88. \(\eta_{\text{fu,k}}\) is the viscosity of the molten fuel in cell \(k\)

As the fuel from the radial control volume is ejected into the channel, it is replaced with new fuel from outside the control volume, assumed to carry no radial momentum. Thus, the radial velocity of the fuel has to be recalculated. into the channel, it is replaced with new fuel from outside the control volume, assumed to carry no radial momentum. Thus, the radial velocity of the fuel has to be recalculated.

(16.3-34)\[\begin{split} u_{\text{fu,ca-ch,k}} = u_{\text{fu,ca-ch,k}} \cdot \frac{V_{\text{control}} - V_{\text{ejected}}}{V_{\text{control}}} \\ = u_{\text{fu,ca-ch,k}} \cdot \frac{0.9 R_{\text{ca,k}} - u_{\text{fu,ca-ch,k}} \cdot \Delta t}{0.9 R_{\text{ca,k}}}\end{split}\]

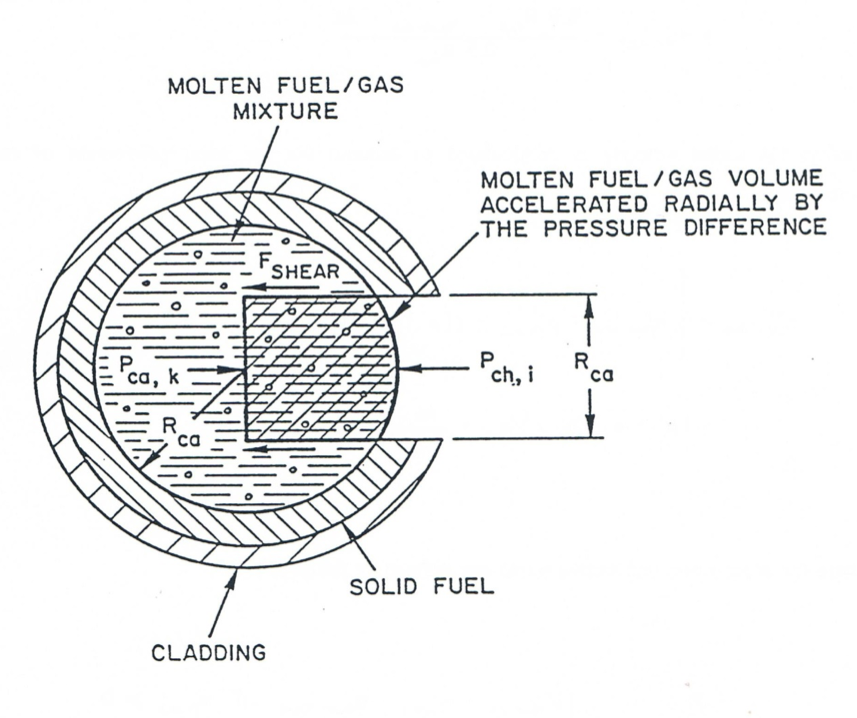
Figure 16.3.1 Geometry for the Radial Acceleration Calculation

Finally, the radial velocity is recalculated to account for the axial convection of radial momentum:

(16.3-35)\[ u_{\text{fu,ca-ch,k}}^{n + 1} = \left\{ u_{\text{fu,ca-ch,k}}^{n + 1} \cdot {\rho'}_{\text{fu,ca,k}} - \left( \left\lbrack {\rho'} \cdot u \cdot u_{\text{ca-ch}} \right\rbrack_{\text{fu,k+1}} - \left\lbrack {\rho'} \cdot u \cdot u_{\text{ca-ch}} \right\rbrack_{\text{fu,k}} \right) \cdot \frac{t}{z_{\text{k}}} \right\} \cdot \frac{1}{{\rho'}_{\text{fu,ca,k}}}\]

where the momentum convective terms are defined as follows:

(16.3-36)\[\begin{split} \left\lbrack {\rho'} \cdot u \cdot u_{\text{ca-ch}} \right\rbrack_{\text{fu,k}} = \begin{cases} {\rho'}_{\text{fu,ca,k-1}} \cdot u_{\text{fu,ca,k}} \cdot u_{\text{fu,ca-ch,k-1}} & \text{if } u_{\text{fu,ca,k}} \geq 0 \\ {\rho'}_{\text{fu,ca,k}} \cdot u_{\text{fu,ca,k}} \cdot u_{\text{fu,ca-ch,k}} & \text{if } u_{\text{fu,ca,k}} < 0 \end{cases}\end{split}\]

The mechanistic ejection model has been compared with the pressure equilibration ejection model (\(\text{INEAEJ} = 0\)) in several calculations. It appears that the pressure equilibration ejection model provides generally a good approximation to the results calculated by the mechanistic model. The larger differences appear during high power excursions and during the time immediately following the pin failure, when the inertial forces accounted for in the mechanistic model delay the early fuel ejection into the channel. It is expected that after validation in several experiment analyses the mechanistic ejection model will become the standard model to be used in SAS4A calculations.

16.3.2. Fuel-pin Disruption

When certain conditions are satisfied, the fuel pins can be totally disrupted at certain axial locations. The decision process which triggers the pin disruption is performed in the LE1PIN routine and has been outlined in Section 16.2. The nodes to be disrupted are flagged in LE1PIN by setting \(\text{IFLAG} \left( I \right) = 9\). The disruption process itself is performed in the LEDISR routine and is described below.

The LEDISR routine first checks whether a node that is to be disrupted is within the physical region for fuel, fission gas, steel and fuel chunks, since all these components are likely to be created via the disruption process. If the node to be disrupted lies outside the fuel physical region, for example, the fuel region will be extended so that the molten fuel generated via the disruption process will be modeled appropriately. Then, the generalized densities and the temperatures of the components present in the channel are reset to account for the addition of mass due to the pin disruption:

(16.3-37)\[ \Delta{\rho'}_{\text{fu,i}} = {\rho'}_{\text{fu,ca,k}}\]

(16.3-38)\[ \Delta{\rho'}_{\text{fi,i}} = {\rho'}_{\text{fi,ca,k}}\]

(16.3-39)\[ \Delta{\rho'}_{\text{f} l \text{,i}} = {\rho'}_{\text{ffc,i}} + \frac{M_{\text{fu,i}} \ \cdot N_{\text{PIN}}}{\Delta z_{\text{i}} \cdot \text{AXMX}}\]

(16.3-40)\[ \Delta{\rho'}_{\text{s} l \text{,i}} = {\rho'}_{\text{sic,i}} + \frac{M_{\text{se,i}} \ \cdot N_{\text{PIN}}}{\Delta z_{\text{i}} \cdot \text{AXMX}}\]

where \(M_{\text{fu,i}}\) and \(M_{\text{se,i}}\) represent the mass of solid stationary fuel and steel, respectively, present in the axial node \(i\), per pin. The temperatures are reset using an energy balance. For example, the new fuel enthalpy is given by:

(16.3-41)\[ h_{\text{fu,i}} = \frac{h_{\text{fu,i}} \cdot {\rho'}_{\text{fu,i}} + h_{\text{fu,ca,k}} \ \cdot \Delta{\rho'}_{\text{fu,i}}}{{\rho'}_{\text{fu,i}} + \Delta{\rho'}_{\text{fu,i}}}\]

The new fuel temperature is obtained from \(h_{\text{fu,i}}\), using the function \(T_{\text{fu}} \left( h \right)\). The velocities are reset using a momentum conservation equation. For example, the new fuel velocity at boundary \(i\), when node \(i\) is disrupted, is calculated as follows:

(16.3-42)\[\begin{split} {u''}_{\text{fu,i}} = \left\lbrack u_{\text{fu,i}} \cdot \left( {\rho'}_{\text{fu,i-1}} + {\rho'}_{\text{s} l \text{,i-1}} \right) \cdot 0.5 \cdot \Delta z_{\text{i-1}} \right. \\ \left. + {u''}_{\text{fu,i}} \cdot \left( {\rho'}_{\text{fu,i-1}} + {\rho'}_{\text{s} l \text{,i-1}} \right) \cdot 0.5 \cdot \Delta z_{\text{i-1}} \right. \\ \left. + u_{\text{fu,ca,k}} \cdot 0.5 \cdot \Delta{\rho'}_{\text{fu,i}} \cdot \Delta z_{\text{i}} \right\rbrack \\ \div \left\lbrack \left( {\rho'}_{\text{fu,i-1}} + {\rho'}_{\text{s} l \text{,i-1}} \right) \cdot 0.5 \cdot \Delta z_{\text{i-1}} \right. \\ \left. + \left( {\rho'}_{\text{fu,i}} + {\rho'}_{\text{s} l \text{,i}} \right) \cdot 0.5 \cdot \Delta z_{\text{i}} \right. \\ \left. + \Delta{\rho'}_{\text{fu,i}} \cdot 0.5 \cdot \Delta z_{\text{i}} \right\rbrack \\\end{split}\]

Disruption of node \(i\) also affects the fuel velocity at the boundary \(i+1\):

(16.3-43)\[\begin{split} {u''}_{\text{fu,i+1}} = \left\lbrack {u'}_{\text{fu,i+1}} \cdot \left( {\rho'}_{\text{fu,i}} + {\rho'}_{\text{s} l \text{,i}} \right) \cdot 0.5 \cdot \Delta z_{\text{i}} \right. \\ \left. + {u''}_{\text{fu,i+1}} \left( {\rho'}_{\text{fu,i+1}} + {\rho'}_{\text{s} l \text{,i+1}} \right) \cdot 0.5 \cdot \Delta z_{\text{i+1}} \right. \\ \left. + u_{\text{fu,ca,k}} \cdot 0.5 \cdot \Delta{\rho'}_{\text{fu,i}} \cdot \Delta z_{\text{i}} \right\rbrack \\ \div \left\lbrack \left( {\rho'}_{\text{fu,i}} + {\rho'}_{\text{s} l \text{,i}} \right) \cdot 0.5 \cdot \Delta z_{\text{i}} \right. \\ \left. + \left( {\rho'}_{\text{fu,i+1}} + {\rho'}_{\text{s} l \text{,i+1}} \right) \cdot 0.5 \cdot \Delta z_{\text{i+1}} \right. \\ \left. + \Delta{\rho'}_{\text{fu,i}} \cdot 0.5 \cdot \Delta z_{\text{i}} \right\rbrack \\\end{split}\]

The velocities \({u'}_{\text{fu,i}}\) and \({u''}_{\text{fu,i}}\) represent the molten fuel velocities at the channel boundary \(i\) and are described in more detail in Section 16.4.2.1.

Finally, the densities are reset as follows:

(16.3-44)\[ {\rho'}_{\text{fu,i}} = {\rho'}_{\text{fu,i}} + \Delta{\rho'}_{\text{fu,i}}\]

(16.3-45)\[ {\rho'}_{\text{fi,i}} = {\rho'}_{\text{fi,i}} + \Delta{\rho'}_{\text{fi,i}}\]

(16.3-46)\[ {\rho'}_{\text{f} l \text{,i}} = {\rho'}_{\text{f} l \text{,i}} + \Delta{\rho'}_{\text{f} l \text{,i}}\]

(16.3-47)\[ {\rho'}_{\text{s} l \text{,i}} = {\rho'}_{\text{s} l \text{,i}} + \Delta{\rho'}_{\text{s} l \text{,i}}\]

The partial pressures are then reset to account for the new gas volume and gas densities in the disrupted node. A number of quantities related to the cladding are set to zero before the end of the routine. These quantities include the perimeter and thickness of cladding and the amount of fuel and steel in the cladding crust.

16.3.3. Fuel Ejection via the Open Pin Stubs

Once the fuel-pin disruption has occurred in a subassembly, the remaining pin stubs can eject fuel and fission gas axially into the disrupted region, in addition to the regular radial gas ejection. Fuel and fission gas can also reenter the fuel-pin stubs when the pressure in the disrupted region exceeds the pressure in the pin cavity. The ejection (or reentry) of the molten fuel via the open pin stubs is calculated by solving the momentum conservation equation for the cavity half-cells adjacent to the disrupted region. This equation is solved in the routine LE1PIN. It is derived in the same manner as described in the PLUTO2 chapter for all regular in-pin momentum cells, but using the cell geometry illustrated in Figure 16.3.2. The momentum cell for the bottom pin stub extends from the center of the cell \(\text{IDISBT-1}\) to the end of the stub. The pressure difference used in the momentum equation is \(P_{\text{IDISBT}} - P_{\text{ca,IDISBT-1}}\), where \(P_{\text{IDISBT}}\) is the pressure in the disrupted region the convective flux coming from the disrupted region is defined using the generalized density \({\rho'}_{\text{fu,IDISBT}}\), i.e., the fuel generalized density in the disrupted region.

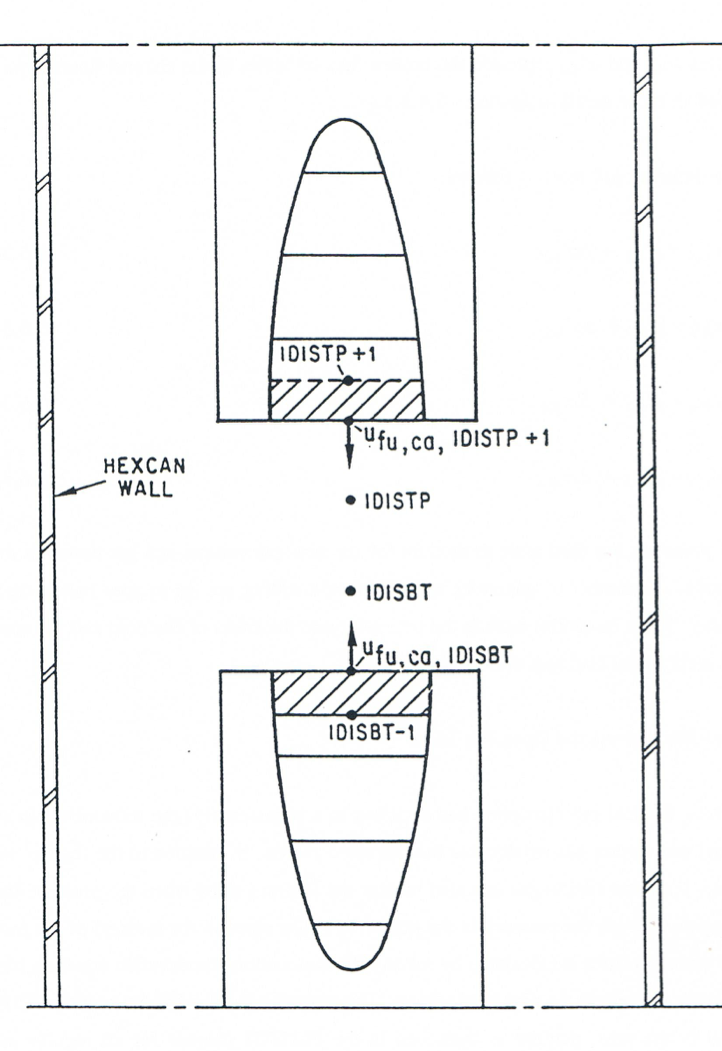
Figure 16.3.2 Geometry Used in the Derivation of the Momentum Equations for Ejection via the Pin Stubs