16.5. Freezing, Melting and Heat-transfer Processes Related to Stationary Pin Stubs and Hexcan Wall

16.5.1. Physical Models

The models presented in this section describe a series of physical processes related to the stationary pin stubs and the hexcan wall. Except for the heat transfer in the cladding and in the hexcan wall, the processes described lead to geometry changes that affect directly the hydrodynamic model of the coolant channel.

One of the most important phenomena during a LOF accident is the freezing of the initially molten fuel and the formation of the fuel crusts. The molten fuel ejected from the pin cavity is accelerated in the coolant channel by the local pressure gradients and begins to move toward the extremities of the channel. In the process, however, it exchanges heat with the sodium, cladding and structure, all of which have a temperature well below the fuel freezing temperature. Eventually the fuel will begin to freeze, forming stationary fuel crusts on the cladding and/or structure or leading to the formation of solid fuel chunks which continue to move in the channel. Steel freezing can also occur occasionally, particularly at locations where the molten steel is the dominant component and is in contact with cold cladding or structure. The freezing of steel leads, in LEVITATE, to a local increase in the thickness of the cladding and/or structure, rather than to the formation of a distinct steel crust.

The fuel crusts formed at various axial locations can begin to melt if the power level increases, thus releasing the fuel again and allowing it to move in the coolant channel. Another mechanism which could also release the fuel crust is the crust breakup, which can occur when the underlying steel support melts and the crust becomes unstable. The continuous heating of the cladding and hexcan wall leads eventually to steel melting. The molten steel is ablated, becoming part of the moving components in the channel, and the thickness of the cladding and/or structure is reduced, increasing the flow area of the coolant channel.

In a similar manner, the solid fuel and steel chunks generated via the fuel-pin disruption can begin to melt due to the direct heating and heat exchange with other components. This will result in a transfer of fuel from the chunk field to the molten fuel field in the coolant channel. This transfer of mass is accompanied by a transfer of energy and momentum as well as a change in the geometry of the solid chunks.

16.5.2. Description of the Method of Solution and Logic Flow

The heat-transfer equations in the cladding and structure, which are not directly related to a geometry change, are solved in the LESOEN routine, i.e., while advancing the solution for the hydrodynamic model in the channel. All other processes related to the stationary pin stubs and to the hexcan wall involve a change in the local geometry and the routines describing them are called after completing the solution for both the in-pin and coolant channel hydrodynamic models. All melting/freezing processes modeled here affect the hydrodynamic parameters of the coolant channel. Changes in the local temperatures, velocities, or pressures are performed in each of the routines described below, whenever necessary. The routine LELUME (LEVITATE CHUNK-LU MELTING) calculates the melting and the size changes of the solid fuel/steel chunks at all axial locations. The routine LEFREZ (LEVITATE FREEZING AND MELTING) then models a series of important processes, such as fuel/steel freezing and crust formation, fuel/steel chunk formation, fuel crust remelting and breakup. Next called is the routine LEABLA (LEVITATE ABLATION) which calculates the gradual melting and ablation of the cladding and hexcan wall. The routine LEDISR (LEVITATE DISRUPTION) performs the disruption of the fuel pin, whenever a disrupt node is predicted. The disruption, which can occur in one or more nodes in any time step, leads to changes in geometry, mass, energy and pressure for various components present in the respective cell. Finally, the routine LESRME (LEVITATE STRUCTURE MELTING) calculates the rupture of the hexcan wall due to melting and/or pressure burst effects.

16.5.3. Fuel/steel Freezing and Crust Formation

The calculation of fuel/steel freezing is performed in the routine LEFREZ. The fuel flow regimes lead to a situation very different from the steel flow regimes in terms of freezing and are treated separately.

16.5.3.1. The Freezing Process when a Fuel Flow Regime is Present

In this case, the molten steel component exists in the form of droplets imbedded in the molten fuel and has a temperature well above freezing. Thus, only the freezing of the molten fuel must be considered. The freezing calculation decides what amount of fuel, if any, will freeze in each node during the current time step. It also has to decide where the frozen fuel will go, when leaving the moving molten-fuel field. Three possibilities exist:

1. The freezing fuel will form (or add to) a crust on the cladding; (when the cladding has been completely ablated, the fuel can freeze on the bare fuel pins).

2. The freezing fuel will form (or add to) a crust on the hexcan wall (Figure 16.5.1).

3. The freezing fuel will generate solid fuel chunks, which will be added to the chunk field

The freezing calculation begins by examining the enthalpy of the molten fuel:

1. If \(h_{\text{fu,i}} > h_{\text{fu,freeze}}\), no fuel freezing occurs. The enthalpy \(h_{\text{fu,freeze}}\) is an input parameter, i.e., \(h_{\text{fu,freeze}} = \text{EGBBLY}\). It has to satisfy the conditions:

(16.5-1)

\[h_{\text{fu,so}} < h_{\text{fu,freeze}} < h_{\text{fu,liq}}\]

1. If \(h_{\text{fu,i}} < h_{\text{fu,so}}\), rapid fuel freezing occurs, leading to the formation of solid fuel chunks only. In order to avoid numerical problems, only one tenth of the fuel mass \(\left( 0.1 \cdot \rho_{\text{fu,i}} \cdot A_{\text{fu,i}} \cdot \Delta z_{\text{i}} \right)\) in the cell is allowed to freeze in each time step under these circumstances.

2. If \(h_{\text{fu,so}} < h_{\text{fu,i}} < h_{\text{fu,freeze}}\), only partial fuel freezing is allowed to occur. The amount of freezing fuel is determined as follows:

(16.5-2)

\[\Delta {\rho'}_{\text{fu,i}} = {\rho'}_{\text{fu,i}} \cdot \frac{h_{\text{fu,freeze}} \ - h_{\text{fu,i}}}{h_{\text{fu,freeze}} - h_{\text{fu,so}}}\]

The area occupied by this newly frozen fuel is:

(16.5-3)

\[\Delta A_{\text{fu,i}} = \frac{\Delta{\rho'}_{\text{fu,i}}}{\rho_{\text{fu,so}}} \cdot \text{AXMX}\]

The assumption is made that the fuel looses most of he energy at the channel boundaries, i.e., by exchanging heat with the cladding and hexcan wall. Thus, the frozen fuel is first used to form a fuel crust on the solid boundaries. The distribution of \(\Delta {\rho'}_{\text{fu,i}}\) between the clad and hexcan wall is made as follow:

(16.5-4)

\[\Delta {\rho'}_{\text{fu,cl,i}} = \Delta {\rho'}_{\text{fu,i}} \cdot \frac{\text{WTCL}}{\text{WTCL} + \text{WTSR}}\]

(16.5-5)

\[\Delta {\rho'}_{\text{fu,sr,i}} = \Delta {\rho'}_{\text{fu,i}} \cdot \frac{\text{WTSR}}{\text{WTCL} + \text{WTSR}}\]

where the weights WTCL and WTSR are:

(16.5-6)

\[\text{WTCL} = A_{\text{cl,i}}^{L} \cdot \left\lbrack \left( T_{\text{fu,i}} - T_{\text{cl,i}} \right) \cdot C_{\text{mfu,cl,i}} \ + \left( T_{\text{fu,i}} - T_{\text{ffc,i}} \right) \cdot C_{\text{ff,cl,i}} \right\rbrack\]

(16.5-7)

\[\text{WTSR} = A_{\text{sr,i}}^{L} \cdot \left\lbrack \left( T_{\text{fu,i}} - T_{\text{sr,i}} \right) \cdot C_{\text{mfu,sr,i}} \ + \left( T_{\text{fu,i}} - T_{\text{ffs,i}} \right) \cdot C_{\text{ff,sr,i}} \right\rbrack\]

Occasionally, one or both of these weights can be set to zero. This happens for \(\text{WTCL}\) when the cladding surface is molten and thus no solid support for freezing exists or when the pins are totally disrupted in the cell considered. In these cases, \(\text{WTCL} = 0\).

Similarly, \(\text{WTSR} = 0\) whenever the hexcan wall surface is molten and no crust formation can occur. In this case, we will still use Eqs. 16.5-4 and 16.5-5 to calculate the distribution of the frozen fuel between cladding and hexcan wall. The situation can arise, however, where the amount of frozen fuel is too large for the available freezing area. For example, let us assume that the cladding surface is molten and \(\text{WTCL} = 0\). In this case, we can have:

(16.5-8)

\[\Delta A_{\text{fu,i}} > A_{\text{ch,op,sr}}\]

where

(16.5-9)

\[A_{\text{ch,op,sr}} = A_{\text{ch,sr}} - A_{\text{ff,sr}}\]

(16.5-10)

\[A_{\text{ff,sr}} = L_{\text{ff,sr}} \cdot l_{\text{ff,sr}}\]

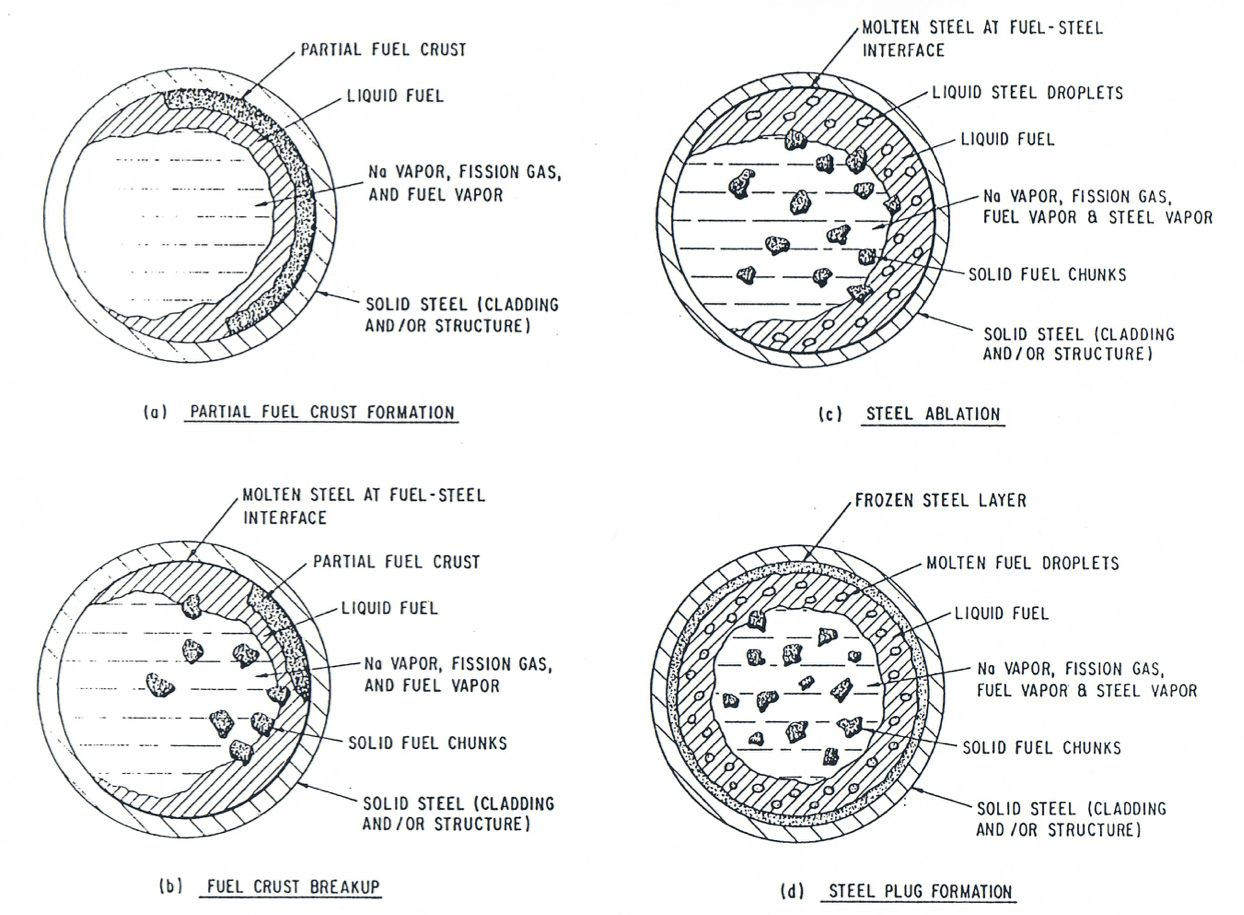
Figure 16.5.1 Freezing, Melting and Crust Breakup Processes

and the elements used in Eqs. 16.5-7 and 16.5-8 have been defined in Section 16.4.3.9. If Eq. 16.5-6 is satisfied, only an amount of fuel consistent with the available area is allowed to freeze on the structure, while the remaining fuel generates solid chunks:

(16.5-11)

\[\Delta {\rho'}_{\text{fu,sr,i}} = \frac{\rho_{\text{fu,so}} \cdot A_{\text{ch,op,sr}}}{\text{AXMX}}\]

(16.5-12)

\[\Delta {\rho'}_{\text{fu,lu,i}} = \Delta{\rho'}_{\text{fu,i}} - \Delta {\rho'}_{\text{fu,sr,i}}\]

When both \(\text{WTCL} = 0\) and \(\text{WSTR} = 0\) all the freezing fuel is used to generate solid fuel chunks:

(16.5-13)

\[\Delta {\rho'}_{\text{fu,} l \text{u,i}} = \Delta {\rho'}_{\text{fu,i}}\]

Another decision that has to be made in connection with the fuel freezing is the steel entrapment in the frozen fuel. Based on experimental evidence obtained in the posttest examination of several fuel motion tests, it appears that only small steel droplets are trapped in the frozen fuel. LEVITATE assumes that small droplets exist only when small amounts of steel are locally present. Otherwise, the steel exists in large droplets that will tend to separate from the freezing fuel. Thus, if:

(16.5-14)

\[\frac{\theta_{\text{se,i}}}{\theta_{\text{fu,i}}} > 0.1\]

no steel entrapment occurs. Otherwise, the amount of steel trapped in the frozen fuel is calculated from:

(16.5-15)

\[\Delta {\rho'}_{\text{se,i}} = {\rho'}_{\text{se,i}} \cdot \frac{\Delta {\rho'}_{\text{fu,i}}}{{\rho'}_{\text{fu,i}}}\]

The actual geometry of the fuel crust (i.e. thickness and area coefficient) is not changed in LEFREZ when fuel freezing occurs. The geometry is changed in LEGEOM at the beginning of the next time step. The geometry of the chunks is changed in LEFREZ due to the condition of the new chunks. The radius of the resulting chunks is a mass-weighted average of the chunks being combined. A more detailed discussion about the chunk geometry can be found in Section 16.4.3.9.

16.5.3.2. The Freezing Process when a Steel Flow Regime is Present

In a steel flow regime, both steel freezing and fuel freezing can occur. The molten fuel is in the form of droplets imbedded in the molten steel and can freeze as it approaches the steel temperature. The amount of fuel freezing in cell \(i\), \(\Delta {\rho'}_{\text{fu,i}}\) is calculated using the same procedure outline in Section 16.5.3.1. However, because no direct contact between the freezing fuel and the channel boundaries exists, crust formation cannot occur. All freezing fuel is used to generate solid fuel chunks:

(16.5-16)

\[\Delta {\rho'}_{\text{fu,} l \text{u,i}} = \Delta {\rho'}_{\text{fu,i}}\]

The steel-freezing calculation follows the same lines as the fuel calculation, but is keyed to the steel temperature rather than enthalpy:

1. If \(T_{\text{se,i}} > T_{\text{se,freeze}}\), no steel freezing occurs. The temperature \(T_{\text{se,freeze}}\) is determined using the input parameter \(\text{FRMRSE}\):

(16.5-17)

\[T_{\text{se,freeze}} = T_{\text{se,so}} + \left( T_{\text{se,} l \text{q}} - T_{\text{se,so}} \right) \cdot \text{FRMRSE}\]

1. If \(T_{\text{se,i}} < T_{\text{se,so}}\), rapid steel freezing occurs, leading to the formation of steel chunks only.

2. If \(T_{\text{se,so}} < T_{\text{se,i}} < T_{\text{se,freeze}}\), only partial steel freezing is allowed to occur. The amount of freezing steel is calculated from:

(16.5-18)

\[\Delta {\rho'}_{\text{se,i}} = {\rho'}_{\text{se,i}} \cdot \frac{T_{\text{se,freeze}} - T_{\text{se,i}}}{T_{\text{se,freeze}} - T_{\text{se,so}}}\]

The steel can freeze on the cladding and/or on the hexcan wall, leading to an increase in the thickness of these structures. This increase is uniformly distributed along the perimeter, as opposed to the partial crust formed initially in the fuel flow regimes (Figure 16.5.1). The distribution of \(\Delta {\rho'}_{\text{sei}}\), follows the same procedure presented in Section 16.5.3 for fuel. If not all the freezing steel can be distributed between cladding and structure (e.g., in a cell where the pins have been disrupted and/or the hexcan wall surface is molten), part or all of the freezing steel is used to generate solid steel chunks, as appropriate.

16.5.4. Fuel Crust Breakup and Remelting

The fuel crust formation on the cladding and the fuel crust formed on the hexcan wall are completely independent. Either one can be present in any axial cell, having its own temperature and geometry. The formation of the crusts was explained in Section 16.5.3. Once present, the fuel crust can disappear in two ways: via breakup and via remelting. These processes can occur in any flow regime modeled by LEVITATE.

16.5.4.1. Fuel Crust Breakup

It is assumed that the frozen fuel crust is unstable and is allowed to break up whenever there is no underlying solid support. In general, this means that the underlying steel is molten. However, when fuel crusts are present on bare fuel pins, the underlying support is also fuel. Thus, the breakup of the crust on the clad will occur when:

(16.5-19)

\[T_{\text{cl,os}} > T_{\text{se,} l \text{q}}\]

In this case, a gradual but fairly rapid breakup occurs. The crust is reduced each time step by:

(16.5-20)

\[\Delta {\rho'}_{\text{ffc}} = {\rho'}_{\text{ffc}} \cdot \text{CIBREK}\]

where \(\text{CIBREK} = 0.01\) is a built-in constant, defined in the routine \(\text{LEFREZ}\). Both the thickness \(1_{\text{ff,cl,i}}\) and the length (i.e., the area coefficient \(C_{\text{ff,c} l \text{,i}}\)) are reduced proportionately:

(16.5-21)

\[1_{\text{ff,cl,i}} = 1_{\text{ff,cl,i}} \cdot \sqrt{1 - \text{CIBREK}}\]

(16.5-22)

\[C_{\text{ff,cl,i}} = C_{\text{ff,cl,i}} \cdot \sqrt{1 - \text{CIBREK}}\]

The fuel breaking loose from the crust generates chunks, which are then merged if necessary with the chunks already present in the cell. If steel inclusions are present in the crust, they are also reduced proportionately and added to the steel chunk field. A similar procedure is used for the structure crust breakup. The process is illustrated in Figure 16.5.1.

16.5.4.2. Remelting of the Fuel Crust

If the fuel crusts are present in a cell and breakup does not occur, the crust can still disappear via remelting. Melting of the cladding crust occurs if:

(16.5-23)

\[T_{\text{ffc,i}} > T_{\text{fu,melt}}\]

where

(16.5-24)

\[T_{\text{fu,melt}} = \left( T_{\text{fu,so}} + T_{\text{fu,} l \text{q}} \right) \cdot 0.5\]

The amount of fuel crust melting in one time step is given by:

(16.5-25)

\[\Delta {\rho'}_{\text{ffc,i}} = {\rho'}_{\text{ffc,i}} \cdot \frac{T_{\text{ffc,i}} \ - T_{\text{fu,melt}}}{T_{\text{fu,} l \text{q}} - T_{\text{fu,melt}}}\]

If steel inclusions are present, they are reduced in the same proportion. The resulting molten fuel and steel are added to the molten fuel and steel fields in the channel, respectively.

A similar procedure is used for the remelting of the fuel crust on the hexcan wall.

16.5.5. Cladding and Hexcan Ablation

When the coolant channel contains molten fuel, which is in an annular or bubbly flow regime, the temperature at the cladding surface rises rapidly, leading to steel melting and ablation. These processes are modeled in the routine \(\text{LEABLA}\). The melting occurs only at the surface, while the bulk of the cladding can remain below the melting point. To model this situation, the cladding is divided into two radial cells, with a thick inner cell and a thin cell at the outer surface (Figure 16.5.2). The thin cladding cell at the outer surface has a small thermal capacity and is thus quite sensitive to variations in the magnitude of the boundary heat fluxes. This cell is of key importance in the melting and ablation process. Ablation of the cladding can occur only if no fuel crust is present on cladding and:

(16.5-26)

\[T_{\text{cl,os,i}} > T_{\text{se,ablation}}\]

where

(16.5-27)

\[T_{\text{se,ablation}} = \left( T_{\text{se,so}} + T_{\text{se,} l \text{q}} \right) \cdot 0.5\]

The fraction of the outer cell mass which is ablated is given by:

(16.5-28)

\[F_{\text{ablation,i}} = \frac{T_{\text{cl,os,i}} - T_{\text{se,ablation}}}{T_{\text{se,} l \text{q}} - T_{\text{se,ablation}}}\]

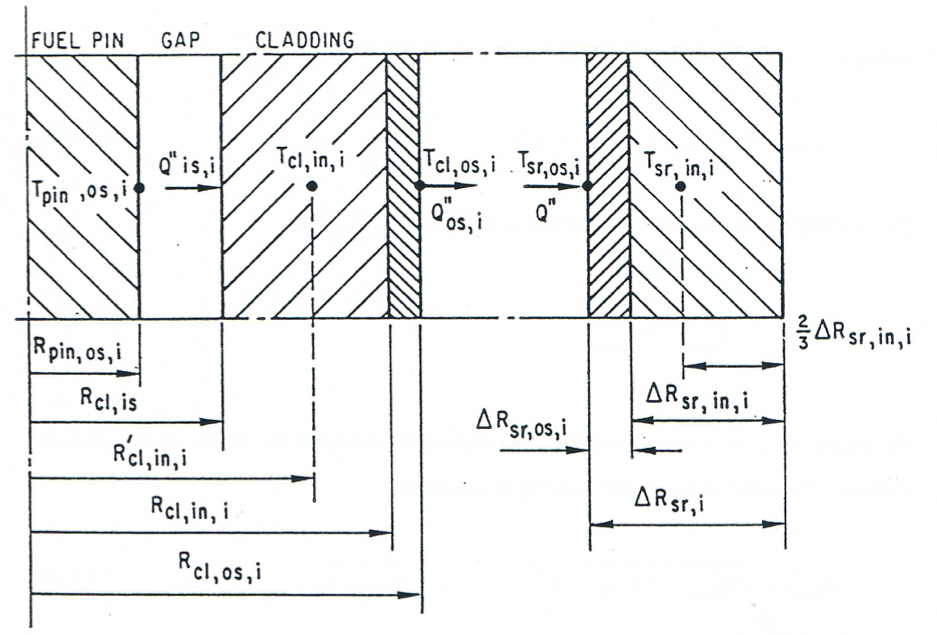
Figure 16.5.2 Temperature Grid in the Cladding and Structure

An amount \(\Delta {\rho'}_{\text{se}}\) is removed from the outer clad cell and added to the molten steel field in the channel. The outer radius of the cladding is changed to:

(16.5-29)

\[R_{\text{cl,os,i}} = \sqrt{R_{\text{cl,in,i}}^{2} - \left( R_{\text{cl,os,i}}^{2} \ - R_{\text{cl,in,i}}^{2} \right) \cdot \left( 1 - F_{\text{ablation,i}} \right)}\]

Due to the explicit solution technique used in the cladding temperature calculation, a very thin outer cladding cell can lead to numerical instabilities in the temperature calculation or alternatively might require very small time steps. To avoid this difficulty while still maintaining an explicit method of solution in the temperature calculation, a lower limit \(\Delta R_{\text{min}}\) is imposed on the thickness of the outer cladding cell. Whenever:

(16.5-30)

\[R_{\text{cl,in,i}} = R_{\text{cl,os,i}} - R_{\text{cl,in,i}} \leq \Delta R_{\text{min}}\]

The temperature calculation grid is restructured. The internal radius \(R_{\text{cl,in,i}}\) is set to:

(16.5-31)

\[R_{\text{cl,in,i}} = R_{\text{cl,os,i}} - 2 \cdot \Delta R_{\text{min}}\]

and the temperature of the cladding cells is adjusted appropriately. This process continues until \(R_{\text{cl,in,i}} = R_{\text{cl,is,i}}\), at which time the internal cladding cell disappears completely. The ablation process can still continue until the outer (and only) cladding cell reaches the thickness \(\Delta R_{\text{min}}\). Afterwards, no ablation is allowed until the remaining cladding reaches the melting point, when the cladding is completely removed and the fuel pin begins to transfer energy directly to the flowing components in the channel.

A similar procedure is used for the ablation of the hexcan wall. The ablation process is illustrated in Figure 16.5.1.

16.5.6. Fuel/Steel Chunk Melting

The moving solid chunks in the channel, both fuel and steel, can begin to melt due to heat transfer from the surrounding components and, in the case of the fuel chunks, due to internal heat generation. This process is modeled in the routine \(\text{LELUME}\). The remelting of the fuel chunks occurs when:

(16.5-32)

\[h_{\text{f} l \text{,i}} > h_{\text{f} l \text{,melt}}\]

where

(16.5-33)

\[h_{\text{f} l \text{,melt}} = \left( h_{\text{fu,so}} + h_{\text{fu,} l \text{q}} \right) \cdot 0.5\]

The amount of molten fuel is obtained from:

(16.5-34)

\[\Delta {\rho'}_{\text{f} l \text{,i}} = {\rho'}_{\text{f} l \text{,i}} \cdot \frac{h_{\text{f} l \text{,i}} \ - h_{\text{f} l \text{,melt limit}}}{h_{\text{fu,} l \text{q}} - h_{\text{f} l \text{,melt limit}}}\]

where

(16.5-35)

\[h_{\text{f} l \text{,melt limit}} = \frac{\left( h_{\text{f} l \text{,melt}} - 0.1 h_{\text{fu,} l \text{q}} \right)}{0.9}\]

The quantity \(h_{l l,\text{melt limit}}\) is defined by Eq. 16.5-35 to be slightly below \(h_{l l \text{,melt}}\). When melting occurs, as defined by eq. 16.5-34, the enthalpy of the molten material is \(h_{\text{fu,} l \text{q}}\), and the enthalpy of he remaining chunks is \(h_{l l,\text{melt limit}}\). Because \(h_{l l,\text{melt limit}}\) is lower than \(h_{l l,\text{melt}}\), which is used in Eq. 16.5-32 to trigger the melting process, the continuous melting of very small amounts of fuel is avoided. Melting of the fuel chunks in cell \(i\) will occur only when their enthalpy again reaches \(h_{l l,\text{melt limit}}\). The size of the chunks is decreased appropriately, but their number remains unchanged. The molten fuel is added to the molten fuel in the channel:

(16.5-36)

\[{\rho'}_{\text{fu,i}} = {\rho'}_{\text{fu,i}} + \Delta{\rho'}_{\text{fu,i}}\]

and the energy and velocity of the molten fuel field are adjusted to reflect the addition of the molten fuel resulting from the remelting of the chunks.

A similar procedure is used for melting the steel chunks, which occurs when:

(16.5-37)

\[h_{\text{s} l \text{,i}} > h_{\text{s} l \text{,melt}}\]

where

(16.5-38)

\[h_{\text{s} l \text{,melt}} = \left( h_{\text{se,so}} + h_{\text{se,} l \text{q}} \right) \cdot 0.5\]

The amount of molten steel is obtained from

(16.5-39)

\[\Delta {\rho'}_{\text{s} l \text{,i}} = {\rho'}_{\text{s} l \text{,i}} \ \cdot \frac{h_{\text{s} l \text{,i}} - h_{\text{s} l \text{,melt limit}}}{h_{\text{se,lq}} \ - h_{\text{s} l \text{,melt limit}}}\]

16.5.7. Heat-transfer Calculation for the Steel Cladding and the Hexcan Wall

These calculations are performed in the routine LESOEN.

16.5.7.1. Heat-transfer Calculation for the Steel Cladding

The heat-transfer calculation for the steel cladding is performed using the two-node mesh illustrated in Figure 16.5.2. Two energy equations, one for each node, are solved explicitly. Due to ablation the geometry of the two cladding nodes can change in any time step.

The energy conservation equation for the outer cladding node in the axial cell \(i\) is:

(16.5-40)

\[\begin{split}\begin{matrix} \rho_{\text{se}} \cdot \frac{\partial \text{h}_{\text{cl,os,i}}}{\partial \text{t}} \cdot \left( R_{\text{cl,os,i}}^{2} - R_{\text{cl,in,i}}^{2} \right) \cdot \pi \cdot \Delta z_{\text{i}} \\ = k_{\text{se}} \cdot \frac{T_{\text{cl,in,i}} - T_{\text{cl,os,i}}}{R_{\text{cl,os,i}} - {R'}_{\text{cl,in,i}}} \cdot 2 \pi R_{\text{cl,in,i}} \cdot \Delta z_{\text{i}} - \sum_{\text{j}}{H_{\text{cl,j,i}}} \\ \cdot \left( T_{\text{cl,os,i}} - T_{\text{j,i}} \right) \cdot \frac{A_{\text{cl,j,i}}^{L}}{N_{\text{pins}}} + Q_{\text{cl,j}} \cdot \frac{R_{\text{cl,os,i}} - R_{\text{cl,in,i}}}{\Delta R_{\text{cl}}^{0}} \\ \end{matrix}\end{split}\]

where the \(\sum_{\text{j}}\) is performed over all the components in the channel that are in contact with the cladding and \(Q_{\text{cl,i}}\) is the energy source in the cladding in cell \(i\). The subscript se refers here to the solid steel, as opposed to the previous occurrences where it was followed by \(i\) (e.g. \(\rho_{\text{se,i}}\)), when it was referring to the molten steel in the channel. After integration over \(\Delta t\), division by \(\Delta z_{\text{i}}\) and rearrangement, e.g., Eq. 16.5-40 becomes:

(16.5-41)

\[\begin{split}\begin{matrix} h_{\text{cl,os,i}}^{n + 1} = h_{\text{cl,os,i}} + \frac{\Delta t}{\rho_{\text{se}} \cdot \pi \left( R_{\text{cl,os,i}}^{2} - R_{\text{cl,in,i}}^{2} \right)} \left\{ \frac{k_{\text{se}} \cdot 2 \pi R_{\text{cl,in,i}}}{R_{\text{cl,os,i}} - {R'}_{\text{cl,in,i}}} \\ \times \left( T_{\text{cl,in,i}} - T_{\text{cl,os,i}} \right) - \frac{\text{AXMX}}{N_{\text{pins}}} \left\lbrack {H'}_{\text{Na,cl,i}} \left( T_{\text{cl,os,i}} - T_{\text{Na,i}} \right) \\ + {H'}_{\text{fu,cl,i}} \left( T_{\text{cl,os,i}} - T_{\text{fu,i}} \right) + {H'}_{\text{se,cl,i}} \left( T_{\text{cl,os,i}} - T_{\text{se,i}} \right) \\ + {H'}_{\text{cl,fi,i}} \left( T_{\text{cl,os,i}} - T_{\text{fl,i}} \right) + {H'}_{\text{cl,sl,i}} \left( T_{\text{cl,os,i}} - T_{\text{sl,i}} \right) \\ + {H'}_{\text{cl,ffc,i}} \left( T_{\text{cl,os,i}} - T_{\text{ffc,i}} \right) \right\rbrack + Q_{\text{cl,i}} \cdot \frac{R_{\text{cl,os,i}} - R_{\text{cl,in,i}}}{\Delta z_{\text{i}} \cdot \Delta R_{\text{cl}}^{o}} \right\} \\ \end{matrix}\end{split}\]

where \({H'}_{\text{j,cl,i}}\) are the generalized heat-transfer coefficients which have been defined previously.

The energy conservation equation for the inner cladding node in the axial cell is shown below:

(16.5-42)

\[\begin{split}\begin{matrix} \rho_{\text{se}} \frac{\partial \text{h}_{\text{cl,in,i}}}{\partial \text{t}} \cdot \left( R_{\text{cl,in,i}}^{2} - R_{\text{cl,is,i}}^{2} \right) \cdot \pi \cdot \Delta z_{\text{i}} \\ = - k_{\text{se}} \frac{T_{\text{cl,in,i}} - T_{\text{cl,os,i}}}{R_{\text{cl,os,i}} - R_{\text{cl,in,i}}} \cdot 2 \pi R_{\text{cl,in,i}} \cdot \Delta z_{\text{i}} \\ + H_{\text{cl,in,pin,i}} \cdot 2 \pi \cdot R_{\text{cl,is,i}} \cdot \Delta z_{\text{i}} \cdot \left( T_{\text{pin,os,i}} - T_{\text{cl,in,i}} \right) \\ + Q_{\text{cl,i}} \cdot \frac{R_{\text{cl,in,i}} - R_{\text{cl,is,i}}}{\Delta R_{\text{cl}}^{o}}~, \end{matrix}\end{split}\]

where \(H_{\text{cl,in,pin,i}}\) is the heat-transfer coefficient between the inner cladding node and the outer fuel node. It takes into account the gap heat conductance and is defined as follows:

(16.5-43)

\[H_{\text{cl,in,pin,i}} = \frac{1}{\frac{1}{H_{\text{gap}}} + \frac{{R'}_{\text{cl,in,i}} - R_{\text{cl,is,i}}}{k_{\text{se}}}}\]

After integration over \(\Delta t\) and rearrangement, Eq. 16.5-42 becomes:

(16.5-44)

\[\begin{split}\begin{matrix} h_{\text{cl,in,i}}^{n + 1} = h_{\text{cl,in,i}} - \frac{\Delta t}{\rho_{\text{se}} \cdot \pi \left( R_{\text{cl,in,i}}^{2} - R_{\text{cl,is,i}}^{2} \right)} \cdot \left\lbrack \frac{k_{\text{se}} \cdot 2 \pi R_{\text{cl,in,i}}}{R_{\text{cl,os,i}} - R_{\text{cl,in,i}}} \\ \cdot \left( T_{\text{cl,in,i}} - T_{\text{cl,os,i}} \right) - H_{\text{cl,in,pin,i}} \cdot 2 \pi R_{\text{cl,is,i}} \\ \cdot \left( T_{\text{pin,os,i}} - T_{\text{cl,in,i}} \right) - Q_{\text{cl,i}} \cdot \frac{R_{\text{cl,in,i}} - R_{\text{cl,is,i}}}{\Delta R_{\text{cl}}^{o} \cdot \Delta z_{\text{i}}} \right\rbrack \\ \end{matrix}\end{split}\]

A special situation occurs whenever the inner cladding node disappears as a consequence of the ablation process, which has been described previously. This situation is indicated by setting the temperature \(T_{\text{cl,in,i}}\), which is not longer used, to a negative arbitrary value, i.e., \(T_{\text{cl,in,i}} = -100\). In this case, the outer cladding node exchanges heat directly with the fuel pin and the energy Eq. 16.5-41 is changed to:

(16.5-45)

\[\begin{split}\begin{matrix} h_{\text{cl,os,i}}^{n + 1} = {h'}_{\text{cl,os,i}} + \frac{\Delta t}{\rho_{\text{se}} \cdot \pi \cdot \left( R_{\text{cl,os,i}}^{2} - R_{\text{cl,in,i}}^{2} \right)} \\ \cdot \left\lbrack - \frac{\text{AXMX}}{N_{\text{pins}}} \cdot \sum_{\text{j}}{{H'}_{\text{cl,j,i}} \left( T_{\text{cl,os,i}} - T_{\text{j,1}} \right)} + H_{\text{cl,os,pin,i}} \cdot 2 \pi R_{\text{cl,in,i}} \\ \cdot \left( T_{\text{pin,os,i}} - T_{\text{cl,os,i}} \right) + Q_{\text{cl,i}} \frac{R_{\text{cl,os,i}} - R_{\text{cl,in,i}}}{\Delta z_{\text{i}} \cdot \Delta R_{\text{cl}}^{o}} \right\rbrack \\ \end{matrix}\end{split}\]

where \(H_{\text{cl,os,pin,i}}\) is the heat-transfer coefficient between the outer cladding node and the outer pin node (when the inner node was vanished):

(16.5-46)

\[H_{\text{cl,os,pin,i}} = \frac{1}{\frac{1}{H_{\text{gap}}} + \frac{R_{\text{cl,os,i}} - R_{\text{cl,os,i}}}{k_{\text{se}}}}\]

The energy transferred between the cladding and the pin in each LEVITATE time step is integrated over the heat-transfer time step and stored under the name \(\text{HFPICL} \left( I \right)\). This quantity is then used in the pin heat-transfer calculation, in the routine PLHTR, as the pin boundary condition at \(R = R_{\text{pin,os,i}}\).

Another special situation is the case when the cladding has been totally ablated, and the moving components in the channel are in direct contact with the fuel pin. For this case, the cladding temperature \(T_{\text{cl,os,i}}\) is set equal to \(T_{\text{pin,os,i}}\):

(16.5-47)

\[T_{\text{cl,os,i}} = T_{\text{pin,os,i}}\]

This allows all heat transfer to the channel components, as well as the freezing/melting processes, to be calculated correctly. Freezing of fuel on the bare fuel pin can still occur, if predicted by the freezing model. This situation can be identified in the output by the presence of undisrupted pin nodes, i.e., \(\text{IDISR} \left( I \right) \neq 1\) with no cladding on them, i.e., \(\text{WICLAD} \left( I \right) = 0\). In these cells, the output will indicate that no inner cladding node is present, i.e., \(T_{\text{cl,in,i}} = -100\), and the temperature printed under \(T_{\text{cl,os,i}}\) will represent the outer temperature of the fuel pin, according to Eq. 16.5-47.

The procedure outlined above is used in the fuel and blanket region of the fuel pin. A similar but simplified procedure is used for the remainder of the pin, where no fuel is present. A zero heat-flux boundary condition is used in these nodes.

The new cladding temperatures are finally obtained from the new enthalpies:

(16.5-48)

\[\begin{align} T_{\text{cl,os,i}}^{n + 1} = T \left( h_{\text{cl,os,i}}^{n + 1} \right) ; && T_{\text{cl,in,i}} = T\left( h_{\text{cl,in,i}}^{n + 1} \right) \end{align}\]

16.5.7.2. Heat-transfer Calculation for the Hexcan Wall

The heat-transfer calculation for the hexcan wall (the hexcan wall is alternatively referred to as structure) is performed using the two-cell mesh illustrated in Figure 16.5.2. The outer structure cell is the cell facing the coolant channel. This cell is fairly thin, and responds rapidly to changes in the heat-transfer from the coolant channel. This is necessary for the correct modeling of the structure ablation process, which has been described previously. It is assumed that no heat transfer occurs at the outer boundary of the hexcan wall, i.e., at the boundary facing the neighboring subassemblies. Because of this condition, and in order to improve the accuracy of the two-node calculation for the fairly thick structure, the temperature in the structure is assumed to have a parabolic variation:

(16.5-49)

\[T \left( \Delta R \right) = a \cdot \Delta R^{2} + b \cdot \Delta R + c\]

where \(\Delta R\) is the radial coordinate measured from the hexcan boundary facing the channel towards the pin. The coefficients \(a\), \(b\), and \(c\) are defined each time step by the conditions:

(16.5-50)

\[\frac{\text{dT}}{\text{d} \left( \text{AR} \right)} \big\rvert_{\Delta \text{R}} = - \Delta R_{\text{sr,i}} = 0\]

(16.5-51)

\[T \left( 0 \right) = T_{\text{sr,os,i}}\]

(16.5-52)

\[T \left( - \Delta R_{\text{sr,os,i}} - \frac{1}{3} \Delta R_{\text{sr,in,i}} \right) = T_{\text{sr,in,i}}\]

Using Eqs. 16.5-50 through 16.5-52, it is found that the temperature gradient at the boundary between the outer and the inner structure nodes is given by:

(16.5-53)

\[\begin{split}\begin{matrix} \frac{\text{dT}}{\text{d} \left( \Delta \text{R} \right)} \big\rvert_{\Delta \text{R} = - \Delta R_{\text{sr,os,i}}} \\ = \left( T_{\text{sr,os,i}} - T_{\text{sr,in,i}} \right) \cdot \frac{18 \cdot \Delta R_{\text{sr,in,i}}}{5\Delta R_{\text{sr,i}}^{2} + 8\Delta R_{\text{sr,i}} \cdot \Delta R_{\text{sr,os,i}} - 4\Delta R_{\text{sr,os,i}}^{2}} \\ \end{matrix}\end{split}\]

This temperature gradient expression will be used in the energy-conservation equations for the structure. The equation for the outer structure cell is written:

(16.5-54)

\[\begin{split}\begin{matrix} \rho_{\text{se}} \cdot \frac{\partial \text{h}_{\text{sr,os,i}}}{\partial \text{t}} \cdot \Delta R_{\text{sr,os,i}} \cdot \Delta z_{\text{i}} \cdot L_{\text{sr,i}} \\ = - k_{\text{se}} \cdot \frac{\partial \text{T}}{\partial\left( \Delta \text{R} \right)} \big\rvert_{\Delta R = - \Delta R_{\text{sr,os,i}}} \cdot \Delta z_{\text{i}} \cdot L_{\text{sr,i}} \\ + \sum_{\text{j}}{H_{\text{sr,j,i}} \cdot \left( T_{\text{j,i}} - T_{\text{sr,os,i}} \right) \cdot A_{\text{sr,j,i}}^{L}} \\ \end{matrix}\end{split}\]

where \(\sum_{\text{j}}\) is performed over all the components in the channel that are in contact with the structure. Although \(\Delta R\) is used as the “radial” coordinate, the hexcan wall is in fact assumed to be flat, with thickness \(\Delta R_{\text{i}}\) and perimeter \(L_{\text{sr,i}}\).

After integration over \(\Delta t\), rearrangement and use of Eq. 16.5-53, the above equation becomes:

(16.5-55)

\[\begin{split}h_{\text{sr,os,i}}^{n + 1} = h_{\text{sr,os,i}} + \frac{\Delta t}{\rho_{\text{se}} \ \cdot R_{\text{sr,os,i}} \cdot {L'}_{\text{sr,i}}} \cdot \left\lbrack - \frac{k_{\text{se}} {L'}_{\text{sr,i}} \ \cdot 18 R_{\text{sr,in,i}}}{5R_{\text{sr,i}}^{2} + 8R_{\text{sr,i}} \cdot R_{\text{sr,os,i}} - 4R_{\text{sr,os,i}}^{2}} \ \cdot \left( T_{\text{sr,os,i}} - T_{\text{sr,in,i}} \right) \\ + {H'}_{\text{Na,sr,i}} \cdot \left( T_{\text{Na,i}} - T_{\text{sr,os,i}} \right) + {H'}_{\text{fu,sr,i}} \ \cdot \left( T_{\text{fu,i}} - T_{\text{sr,os,i}} \right) + {H'}_{\text{se,sr,i}} \cdot \left( T_{\text{se,i}} \ - T_{\text{sr,os,i}} \right) \\ + {H'}_{\text{fl,sr,i}} \cdot \left( T_{\text{fl,i}} - T_{\text{sr,os,i}} \right) + {H'}_{\text{s} l \text{,sr,i}} \ \cdot \left( T_{\text{s} l \text{,i}} - T_{\text{sr,os,i}} \right) + {H'}_{\text{ffs,sr,i}} \cdot \left( T_{\text{ffs,i}} \ - T_{\text{sr,os,i}} \right) \right\rbrack\end{split}\]

where

(16.5-56)

\[{L'}_{\text{sr,i}} = \frac{L_{\text{sr,i}}}{\text{AXMX}}\]

and \({H'}_{\text{j,sr,i}}\) are the generalized heat-transfer coefficients which were defined previously as follows:

(16.5-57)

\[{H'}_{\text{j,sr,i}} = H_{\text{j,sr,i}} \cdot \frac{A_{\text{j,sr,i}}}{\text{AXMX} \cdot \Delta z_{\text{i}}}\]

The new temperature of the structure outer node is then obtained from its enthalpy:

(16.5-58)

\[T_{\text{sr,os,i}}^{n + 1} = T \left( h_{\text{sr,os,i}}^{n + 1} \right)\]

The energy equation for the inner structure cell (i.e., the cell which is not in contact with the coolant channel) is written as follows:

(16.5-59)

\[\begin{split}\begin{matrix} \rho_{\text{se}} \cdot \frac{\partial \text{h}_{\text{sr,in,i}}}{\partial \text{t}} \cdot \Delta R_{\text{sr,in,i}} \cdot \Delta z_{\text{i}} \cdot L_{\text{sr,i}} \\ = k_{\text{se}} \frac{\partial \text{T}}{\partial\left( \Delta \text{R} \right)} \big\rvert_{\Delta \text{R} = - \Delta R_{\text{sr,os,i}}} \cdot \Delta z_{\text{i}} \cdot L_{\text{sr,i}} \\ \end{matrix}\end{split}\]

After integration over \(\Delta t\) and rearrangement, the above equation becomes:

(16.5-60)

\[\begin{split}\begin{matrix} h_{\text{sr,in,i}}^{n + 1} = h_{\text{sr,in,i}} \\ + \frac{\Delta t \cdot k_{\text{se}} \cdot 18 \Delta R_{\text{sr,in,i}} \cdot \left( T_{\text{sr,in,i}} \right)}{\rho_{\text{se}} \cdot \Delta R_{\text{sr,in,i}} \cdot \left( 5 \Delta R_{\text{sr,i}}^{2} + 8 \cdot \Delta R_{\text{sr,i}} \cdot \Delta R_{\text{sr,os,i}} - 4\Delta R_{\text{sr,os,i}}^{2} \right)} \\ \end{matrix}\end{split}\]

The new temperature of the structure node is then obtained from its enthalpy:

(16.5-61)

\[T_{\text{sr,in,i}}^{n + 1} = T \left( h_{\text{sr,in,i}}^{n + 1} \right)\]

A special situation occurs when the “inner” structure cell has disappeared completely as a result of the ablation process. This situation is indicated by setting \(T_{\text{sr,in,i}}\) to an arbitrary negative value, i.e., \(T_{\text{sr,in,i}} = -100\). In this case, only the Eq. 16.5-54 for the outer structure cell is solved in a simplified form. The term \(k_{\text{se}} \frac{\partial \text{T}}{\partial \left( \Delta R \right)} \big\rvert_{\Delta R = - \Delta R_{\text{sr,os,i}}}\) is set to zero, and the final equation is shown below:

(16.5-62)

\[h_{\text{sr,os,i}}^{n + 1} = h_{\text{sr,os,i}} + \frac{\Delta t}{\rho_{\text{se}} \ \cdot \Delta R_{\text{sr,os,i}} \cdot {L'}_{\text{sr,i}}} \cdot \sum_{\text{j}}{{H'}_{\text{j,sr,i}} \ \cdot \left( T_{\text{j,i}} - T_{\text{sr,os,i}} \right)}\]

When the “inner” structure cell has been removed and the outer cell has reached both a minimum thickness and the melting point, the hexcan wall is assumed to be breached. Intersubassembly fuel motion is likely to begin. Theoretically, this should be the end of the LEVITATE calculation and the beginning of a transition-phase calculation. However, the code will only print a warning message and the calculation will continue assuming that the hexcan wall will maintain the minimum thickness, although its temperature has risen above the melting range.