16.4. Coolant Channel Hydrodynamic Model¶
16.4.1. Physical Models¶
16.4.1.1. Geometry¶
The coolant channel described by LEVITATE is delimited by the hexcan wall and the outer surface of the fuel pins. Axially, this channel is limited by the upper and lower sodium plena. Calculations are performed in a 1-D geometry, with the variables being functions of the axial height \(z\). As illustrated in Figure 16.1.1, the area of the coolant channel can vary widely due to the local disruption of the fuel pins, cladding and structure ablation, and fuel/steel blockage formation at various axial locations.
16.4.1.2. Hydrodynamic Models¶
The fluid dynamic models in LEVITATE calculate the motion of the materials in the channel. The materials that are tracked by LEVITATE are:
liquid fuel
liquid steel
sodium (liquid, two-phase mixture or superheated vapor)
fission gas
fuel vapor
steel vapor
solid fuel chunks
solid steel chunks
A separate mass and energy conservation equation is solved for each of these components. Momentum conservation equations are solved for three velocity fields, associated with the following component groups:
sodium, fission gas, fuel vapor, steel vapor
liquid fuel, liquid steel
solid fuel chunks, solid steel chunks
Phase transitions can occur, leading to mass, momentum and energy exchange among various moving components and/or among moving and stationary components. These exchanges are described in Section 16.4.1.5.
16.4.1.3. Structural Models¶
The structural models included in LEVITATE describe the thermodynamic behavior of the stationary components that act as boundaries for the coolant channel. The stationary components modeled in LEVITATE are:
steel cladding
steel hexcan wall
cladding frozen fuel crust (with possible steel inclusions)
hexcan wall frozen fuel crust (with possible steel inclusions)
One or more energy equations are solved for each of these components (e.g., two equations are needed for cladding, that has two radial nodes). Due to freezing/melting processes, mass and energy exchange can take place between these stationary components and the moving components in the channel, as explained in Section 16.4.1.5.
16.4.1.4. Fuel/Steel Flow Regimes¶
As indicated in Section 16.1, the interactions between the different components present in the channel, i.e., mass, energy and momentum transfer, are largely determined by the local configuration which, in turn, is determined by the flow regimes used. The fuel/steel flow regimes modeled in LEVITATE are presented conceptually in Figure 16.4.1. They are a bubbly fuel flow regime, a partial annular fuel flow regime, an annular steel flow regime, and a bubbly steel flow regime. The bubbly fuel channel flow is characterized by the presence of large amounts of liquid fuel, with droplets of molten steel, solid fuel and steel chunks, and bubbles of fission gas and sodium vapor imbedded. There is no relative motion between the steel and fuel, and the relative velocity between the molten fuel and the vapor bubbles is quite low, due to the large drag and inertial forces acting on the bubbles.
As the volume fraction of fuel decreases, the bubbly flow regime is changed to the annular fuel flow regime, with the fuel blanketing the cladding partially or totally and the two-phase sodium/gas mixture flowing at the center of the channel. A stream of solid fuel chunks, interacting with both the two-phase sodium/gas mixture and the liquid fuel streams, can also be present. Molten steel droplets are imbedded in the fuel film. The relative velocities between the fuel and mixture are significantly higher than in the bubbly flow regime.
When molten steel is the dominant component at a certain axial location, the flow regime used can be either an annular or a bubbly steel regime. The bubbly steel flow regime is characterized by the presence of a large amount of molten steel, with droplets of molten fuel, solid fuel and steel chunks, and bubbles of fission gas and sodium vapor imbedded. As the volume fraction of molten steel decreases, the bubbly steel regime is changed to the annular steel flow regime. In this regime, the molten steel totally covers the cladding and the vapor mixture flows at the center of the channel. Molten fuel droplets can be imbedded in the molten steel, and solid fuel and steel chunks can interact with both the vapor mixture and the molten steel. In the Release 1.1 version, a partial annular steel flow regime has been introduced. The steel is assumed to cover the cladding only partially moving in the form of droplets and rivulets. This picture is supported by experimental evidence that indicates that the steel does not wet the cladding. As the local amount of molten steel increases, a full annular steel flow regime can develop. The partial annular steel flow regime is used only when the chunk model is active, i.e. \(\text{ICHUNK} = 1\). If the chunk model is not used, the full annular steel flow regime is still used. It is expected that, as the validation effort continues, the partial annular steel flow regime will be available, regardless of the chunk model option used.
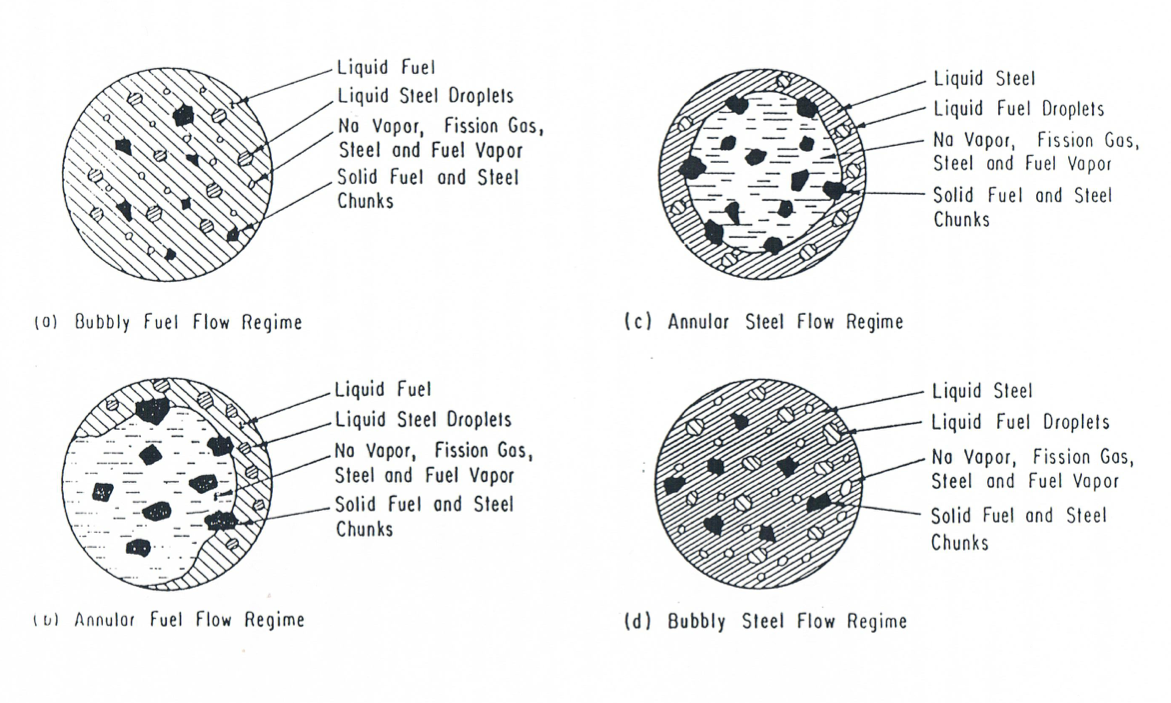
Figure 16.4.1 Continuous Fuel/Steel Regimes Modeled in LEVITATE¶
Because only very limited information is currently available about the fuel-steel flow regime transitions in fuel pin bundles, these transitions are governed in LEVITATE by the fuel-steel volume fraction present at each axial location.
The continuous fuel flow regimes used in LEVITATE have been shown to slow down substantially the fuel dispersal, bringing the results of calculations in close agreement with the experimental data [16-1, 16-11].
16.4.1.5. Mass, Momentum and Energy Exchange (non-convective)¶
Mass, momentum and energy exchange can take place among various components at any given time and location. All these transfers are strongly dependent on the flow regime prevailing at the time and location considered. The mass transfers are due to phase changes (freezing, melting, vaporization, condensation) or to disruption events, such as the disruption of the solid fuel pins or fuel crust breakup. The mass transfer is largely independent of the local flow regime and the allowable transfers are summarized in Figure 16.4.2.
The mass transfer in any given computational cell, together with the changes in the mass of each component due to convection, determine the mass of each component in the cell. These masses, together with the energy from the previous time step, determine the local flow regime and thus the local configuration. The local energy and momentum transfers are strongly dependent on the local flow regime. The allowable energy transfer paths among various LEVITATE components are illustrated in Figure 16.4.3 to Figure 16.4.6 for various flow regimes. Similarly, the allowable momentum paths are illustrated in Figure 16.4.7 through 16.4-10.
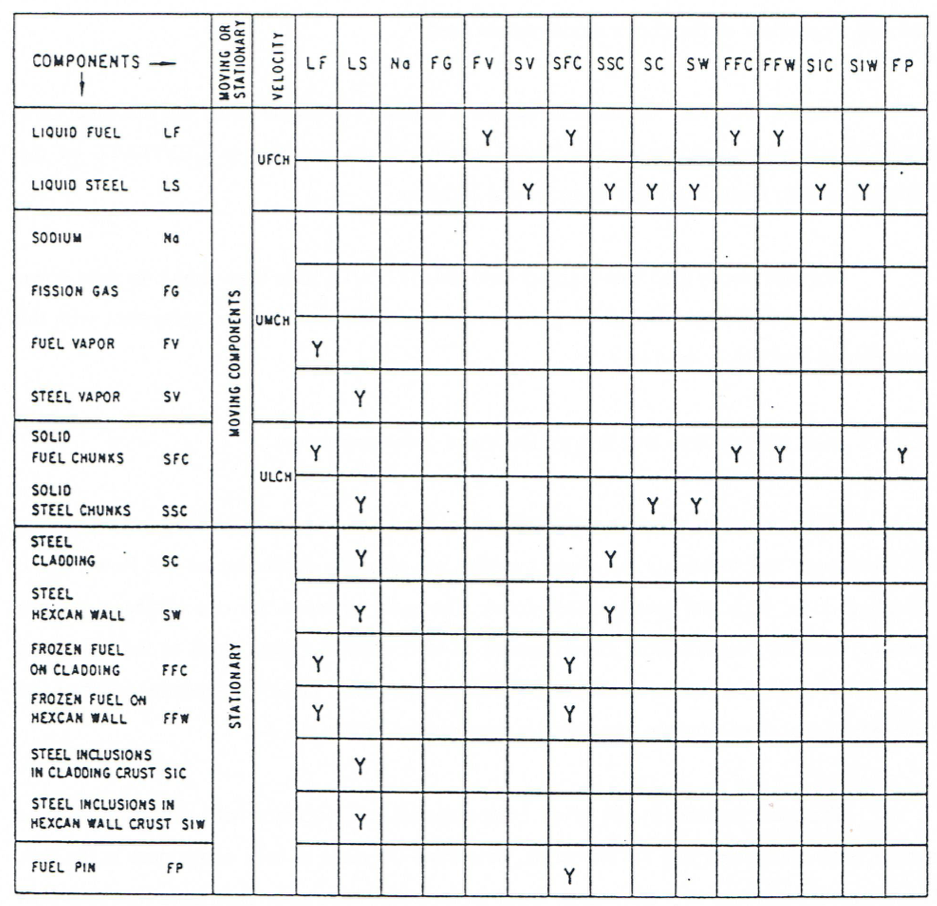
Figure 16.4.2 Mass exchange Possibilities among Various LEVITATE Components¶
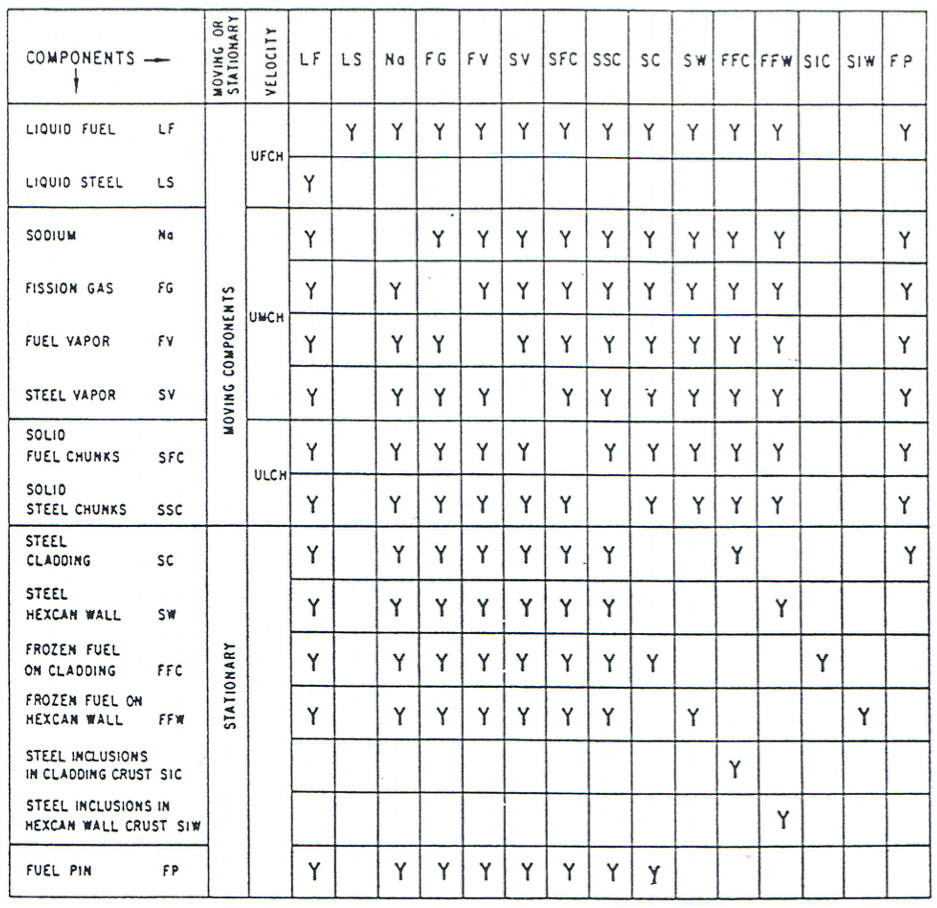
Figure 16.4.3 Energy Exchange Possibilities among Various LEVITATE Components, for the Fuel Annular Flow Regime¶
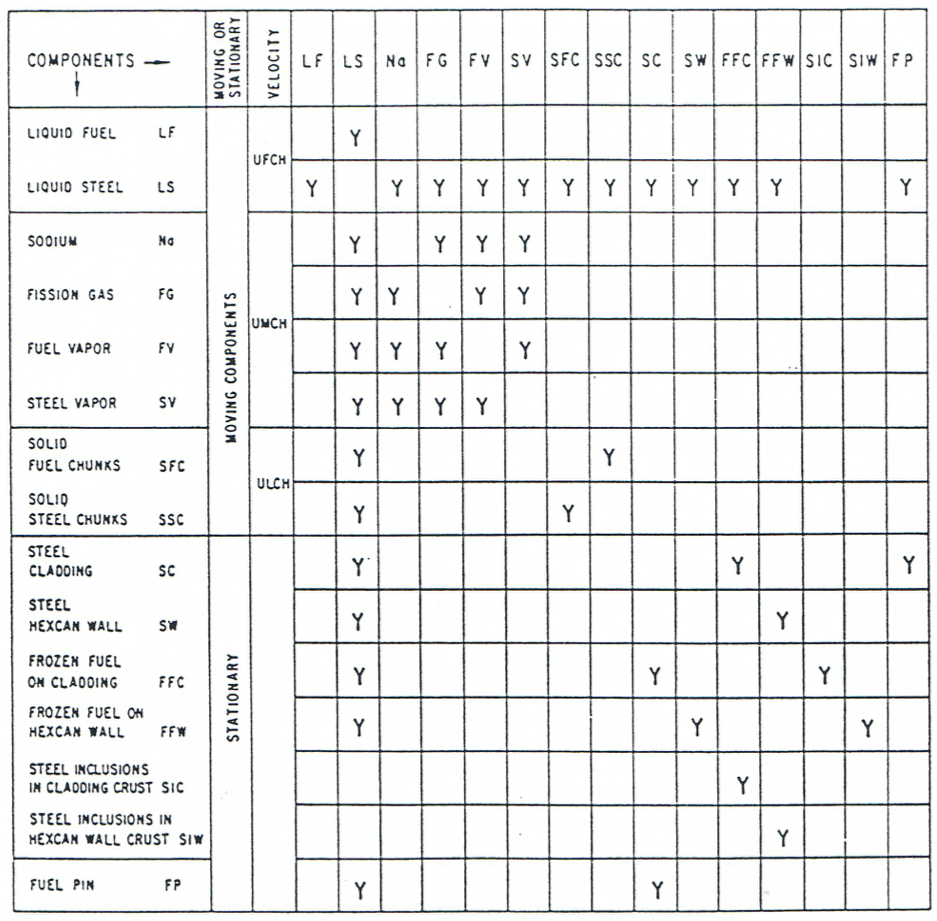
Figure 16.4.4 Energy Exchange Possibilities among Various LEVITATE Components, for the Fuel Bubbly Flow Regime¶
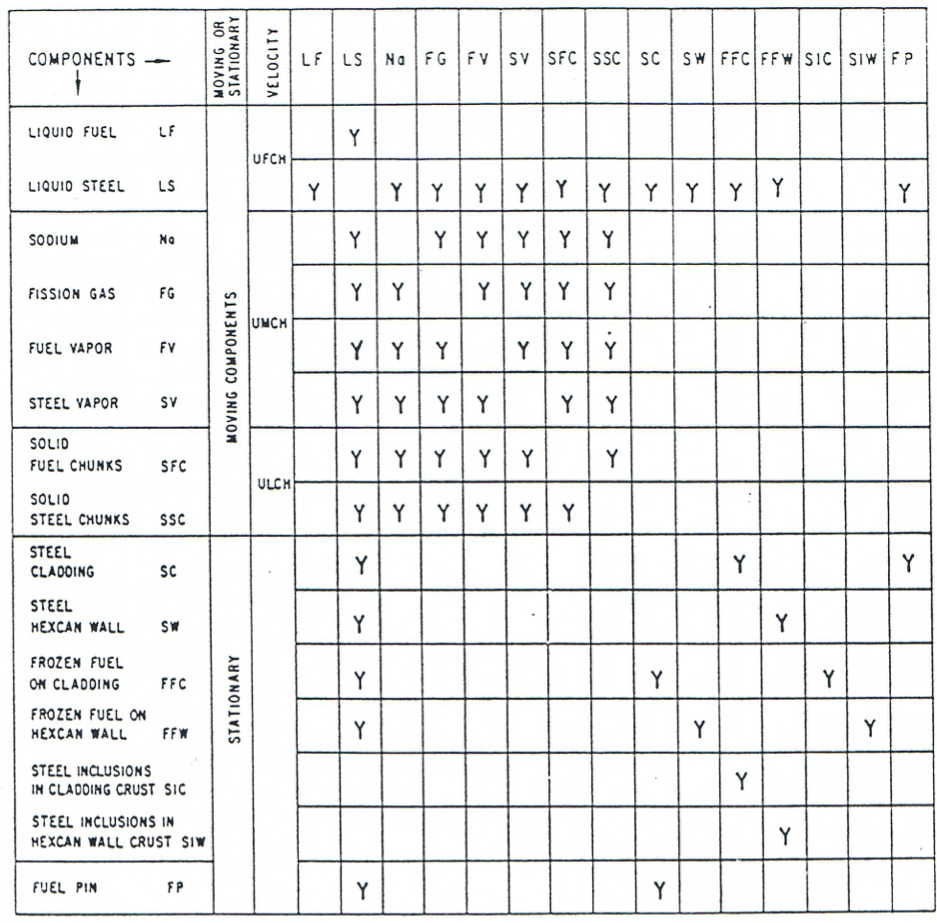
Figure 16.4.5 Energy Exchange Possibilities among Various LEVITATE Components, for the Steel Annular Flow Regime¶
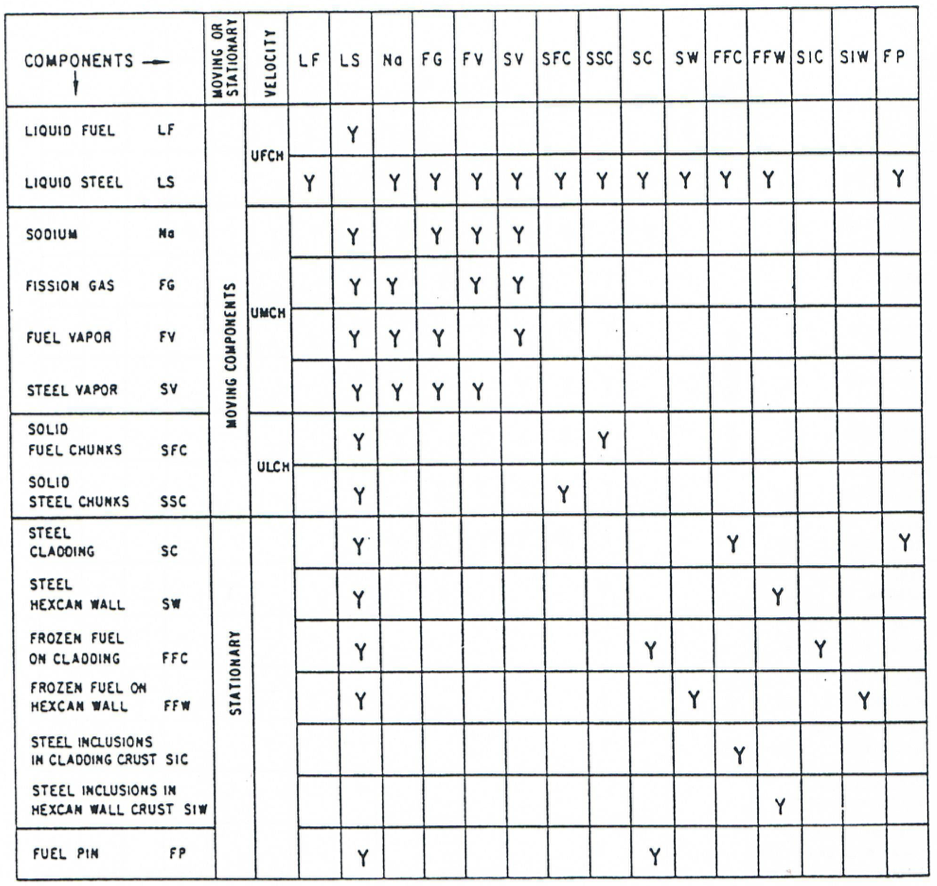
Figure 16.4.6 Energy Exchange Possibilities among Various LEVITATE Components, for the Steel Bubbly Flow Regime¶
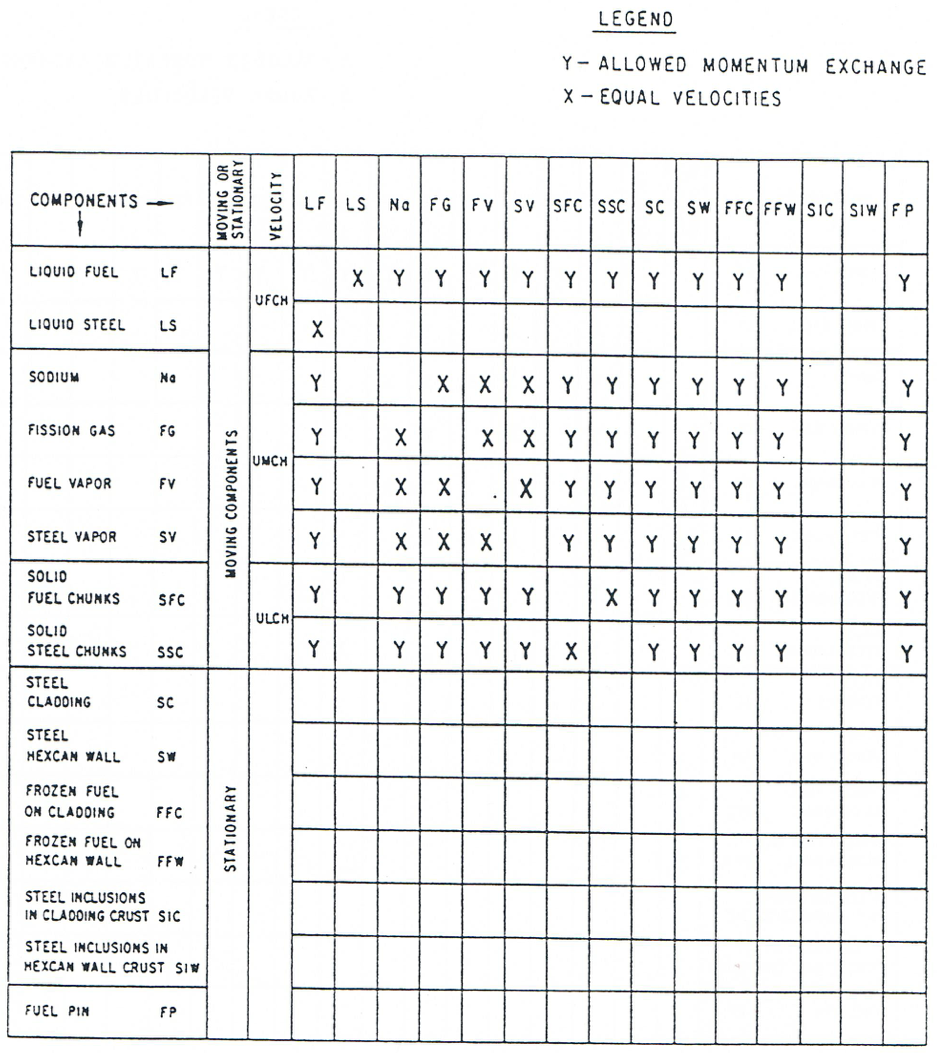
Figure 16.4.7 Momentum Exchange Possibilities among Various LEVITATE Components, for the Fuel Annular Flow Regime¶
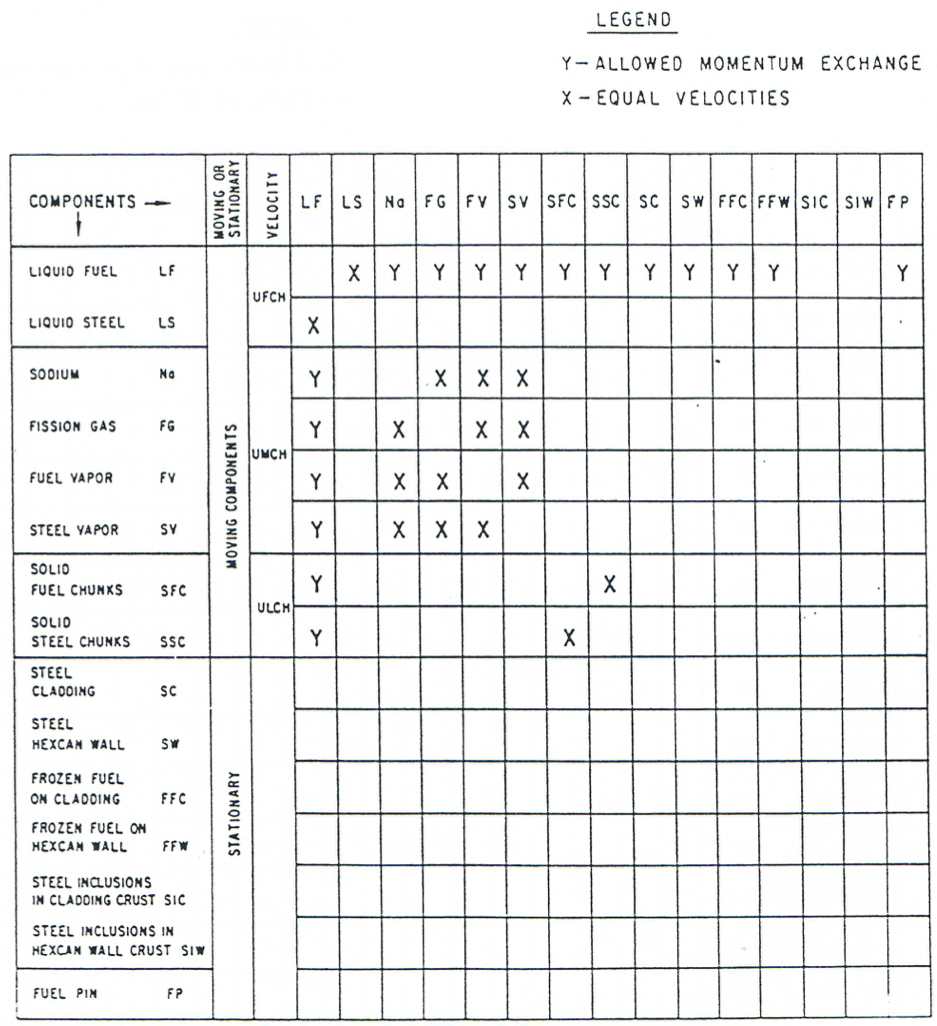
Figure 16.4.8 Momentum Exchange Possibilities among Various LEVITATE Components, for the fuel Bubbly Flow Regime¶
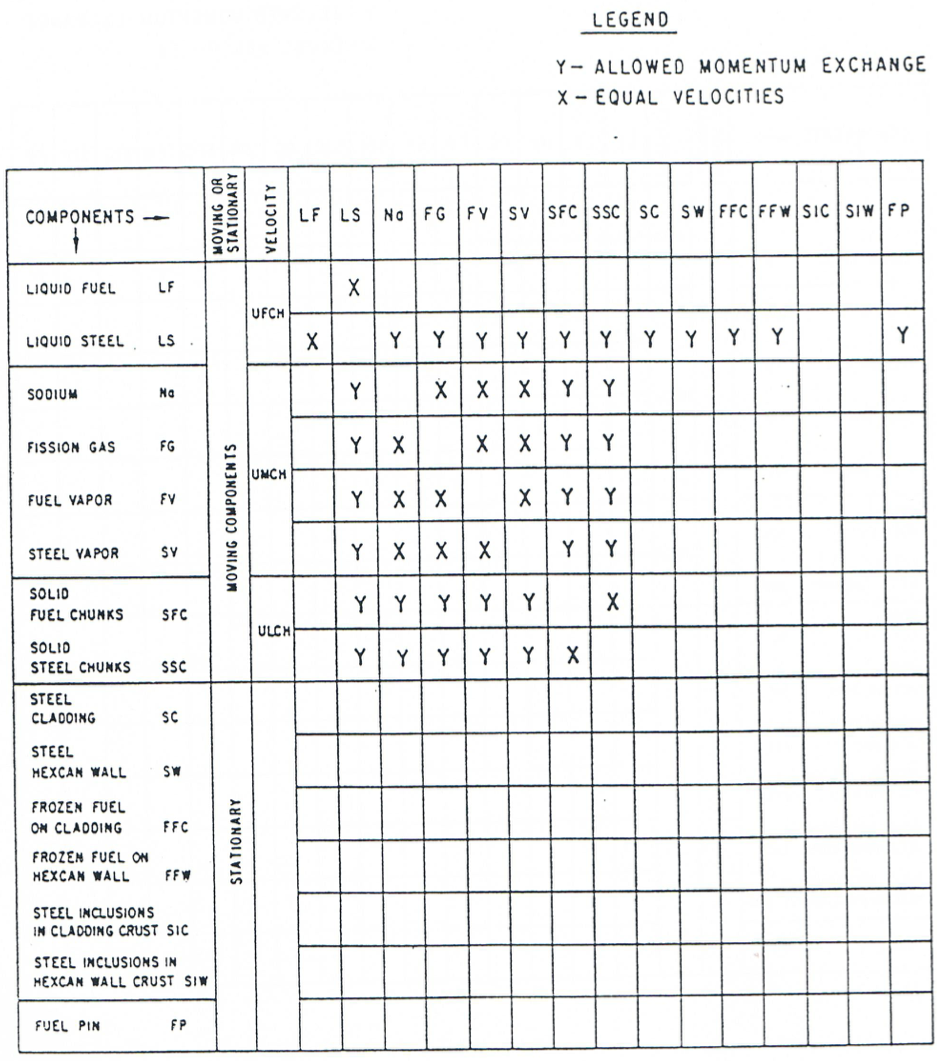
Figure 16.4.9 Momentum Exchange Possibilities among Various LEVITATE Components, for the Steel Annular Flow Regime¶
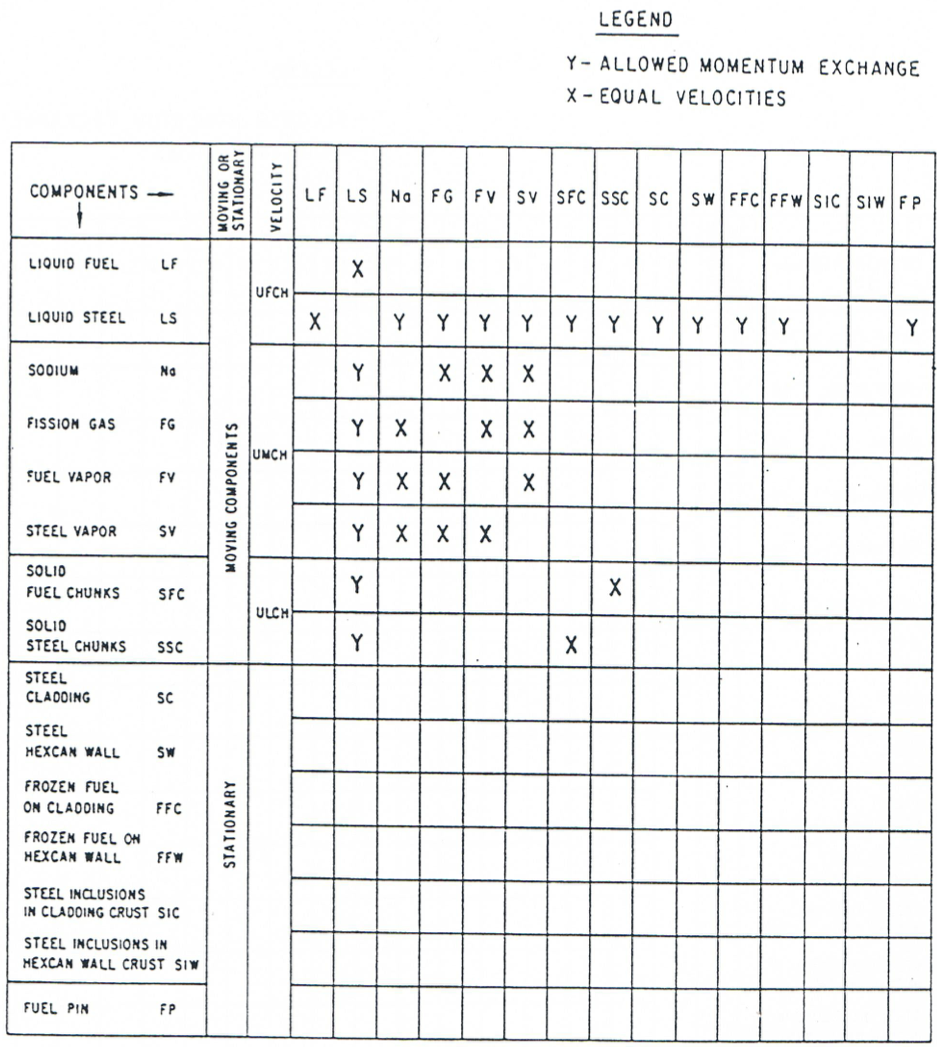
Figure 16.4.10 Momentum Exchange Possibilities among Various LEVITATE Components, for the Steel Bubbly Flow Regime¶
16.4.2. Method of Solution and general Numerical Considerations¶
16.4.2.1. Variables and Mesh Grid Used in Calculations¶
The independent variables used in LEVITATE are the axial coordinate, z, and the time, \(t\). Only one spatial coordinate is necessary, as LEVITATE models the subassembly in a one-dimensional geometry. The dependent variables calculated by the hydrodynamic model for each component, are the generalized density \({\rho'}\), the enthalpy \(h\) (or temperature \(T\)), and the velocity \(u\). The generalized densities have been introduced in Chapter 14 and, for component \(k\), are defined as:
(16.4-1)
where
\(\rho_{\text{k,i}}\) = physical density of component \(k\) at location \(i\)
\(A_{\text{k,i}}\) = cross sectional area occupied by component \(k\) at location \(i\)
\(\text{AXMX}\) = reference area
\(\theta_{\text{k,i}}\) = generalized (area) fraction of component \(k\) at location \(i\)
The mass, energy and momentum partial differential conservation equations are solved using an Eulerian finite difference semi-explicit formulation, as explained below. The mesh grid used for the finite difference formulation is presented in Figure 16.4.11. As indicated in this figure, the densities and enthalpies are defined at the center of each cell, while the velocities are defined at the boundaries. Because of the highly irregular geometry treated by LEVITATE, special attention was necessary for the treatment of abrupt area changes [16-12]. Fuel velocities are defined at each cell boundary, with \(u_{\text{i}}\) being the velocity just before boundary \(i\), and \({u''}_{\text{i}}\) the velocity just after that boundary. The terms “before” and “after” are used in relation to the positive direction of the axial coordinate \(z\).
In order to reduce the numerical diffusion, characteristic of Eulerian numerical schemes, the boundaries of each region containing a certain component are tracked separately as they move through the Eulerian cells.
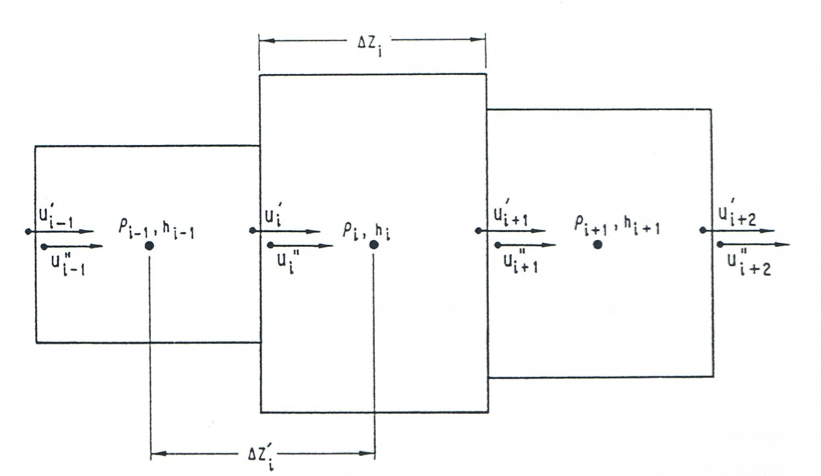
Figure 16.4.11 Mesh Grid used in the Channel Hydrodynamic Model¶
16.4.2.2. Description of the Method of Solution and Logic Flow¶
A simplified modular chart of the LEVITATE model is presented in Figure 16.1.5. The calculation begins by calculating the changes in the position of material boundaries during the current time step. The new interface positions, at the end of the time step, are calculated for all components, except sodium in the LEIF (LEVITATE INTERFACE) routine. The position of the sodium slugs, which determine the boundaries of the sodium region, is calculated in the LEREZO (LEVITATE REZONING) routine. This routine can add (or remove) nodes to the LEVITATE compressible region as the sodium slugs move out of (or into) the channel. The mass conservation equation is solved next, for all components and all axial locations. Each equation is solved explicitly, i.e., the convective fluxes are based on the generalized densities present in each cell at the beginning of the time step. These calculations are performed in the LEMACO (LEVITATE MASS CONSERVATION) routine. The new densities are then used in the LEVOFR (LEVITATE VOLUME FRACTION) routine to determine the volume fraction of each component at each axial location. Using these volume fractions, the LEVOFR routine also determines the flow regime in each axial cell. This flow regime will be assumed to exist in the cell for the duration of the time step. It is worth noting that this is an “implicit type” assumption as the flow regimes are based on the densities calculated at the end of the time step. The next routine called is LEGEOM (LEVITATE GEOMETRY) which determines the geometrical characteristics defining each local configuration. This routine will change the thickness of the fuel crust as necessary or determine the fraction of the cladding circumference covered by the liquid fuel in the partial annular flow regime. In general, LEGEOM calculates the area of contact between various components in various flow regimes. These areas will be used later in calculating the energy and momentum transfer between various components.
The next routine called is LETRAN (LEVITATE TRANSFER) which calculates the heat-transfer and friction coefficients for all axial locations and among all components that are in direct contact. Thus, the code will use the flow regimes present at a certain location to determine which heat transfer and friction coefficients have to be calculated. The allowable exchanges for each flow regime and each component have already been presented in Figure 16.4.3 through Figure 16.4.10. Once contact areas and the corresponding heat-transfer coefficients have been calculated, the energy conservation equation can be solved for all components. The LESOEN (LEVITATE SOLID, LIQUID AND STATIONARY ENERGY EQUATION) routine is called to solve the energy conservation equations for the fuel and steel channels, liquid fuel, liquid steel, stationary cladding, hexcan wall, frozen fuel on the cladding and frozen fuel on the hexcan wall. All equations are solved explicitly, i.e., the convective fluxes are based on beginning of time step densities, thus allowing the axial decoupling of the equations. The energy equation for sodium (two-phase or single-phase vapor) and fission gas is solved in LENAEN (LEVITATE SODIUM-NA ENERGY). The energy equations for fuel and steel vapor are solved in LEFUVA (LEVITATE FUEL VAPOR ENERGY) and LESEVA (LEVITATE STEEL VAPOR ENERGY), respectively. The new temperatures calculated in LENAEN, LEFUVA and LESEVA are used to determine the new pressure of each of the compressible components and thus the total new pressure. The hydrodynamic in-pin model is then used to advance the in-pin solution in the LElPIN and LE2PIN routines. These routines interact with the channel model via the fuel injection process, which is modeled in the LElPIN routine. Molten fuel and fission gas are ejected from the cavity into the channel, leading to changes in the local pressure. The momentum equation for each of the three velocity fields is then solved in the routine LEMOCO (LEVITATE MOMENTUM CONSERVATION). The method of solution is still explicit and the equations are uncoupled axially, but the equations for all three fields are solved simultaneously rather than independently, as was done in the mass and energy equations. Also it is important to note that the pressures used in the momentum equation are the pressures at the end of the time step. The routine called next, LELUME (LEVITATE CHUNK-LU MELTING), calculates the melting and the size changes of the solid fuel/steel chunks at all axial locations. The routine LEFREZ (LEVITATE FREEZING AND MELTING) then models a series of important processes, such as fuel/steel freezing and crust formation, fuel/steel chunk formation, fuel crust remelting and breakup. Next called is the routine LEABLA (LEVITATE ABLATION) which calculates the gradual melting and ablation of the cladding and hexcan wall. The routine LEDISR (LEVITATE DISRUPTION) performs the disruption of the fuel pin whenever a disrupted node is predicted. The disruption, which can occur in one or more nodes in any time step, leads to changes in geometry, mass, energy and pressure for various components present in the respective cell. Finally, the routine LESRME (LEVITATE STRUCTURE MELTING) calculates the rupture of the hexcan wall, due to melting and/or pressure burst effects.
16.4.3. Differential Equations and Finite Difference Equations¶
16.4.3.1. Mass Conservation Equations¶
This section describes the solution of the mass conservation equations for a generic component \(k\), as performed in the routine LEMACO. The region where the \(k\) component is present has been previously updated in the routines LEIF and LEREZO, and is defined by two integers \(i_{\text{k,BT}}\) and \(i_{\text{k,TP}}\), indicating the number of the bottom and top node of the region, respectively. A mass conservation equation is solved for each axial node \(i\), with \(i_{\text{k,BT}} \leq i \leq i_{\text{k,TP}}\). The original mass conservation is written as:
(16.4-2)
No source terms are considered in LEMACO, as all phase changes and injections are treated in separate routines, which will be described later.
After dividing by \(\text{AXMX} \cdot \Delta z_{\text{i}}\) and using the definition of generalized densities, we obtain:
(16.4-3)
Finally, after integrating over the length of the time step, \(\Delta t\), we obtain:
(16.4-4)
or
(16.4-5)
In relation to the use of the superscripts, it is noted that whenever a time-dependent quantity such as \(\left( {\rho'} u \right)\) is written without a superscript, its value is evaluated at the beginning of the computational time step.
The quantity \(\left( {\rho'} u \right)_{\text{k,i-1/2}}\) is the mass convective flux of component \(k\) at the boundary \(i-1/2\) and is calculated using an upstream differencing approach:
If \({u'}_{\text{k,i}} \geq 0\),
(16.4-6a)
If \({u'}_{\text{k,i}} < 0\), then
(16.4-6b)
The velocities \({u'}_{\text{k,i}}\) and \({u''}_{\text{k,i}}\) are correlated by the mass continuity equation across boundary \(i-1/2\):
(16.4-7)
The solution of the mass equation is illustrated below for the molten fuel component. The molten fuel region extends from \(i_{\text{fu,BT}} = \text{IFFUBT}\) to \(i_{\text{fu,TP}} = \text{IFFUTP}\). The first step in the solution is to calculate the convective fuel fluxes at all internal cell boundaries. It is important to note that the convective fluxes defined at boundary \(i-1/2\) have the subscript \(i\), in the code, i.e., \(\text{COFUCH} \left( I \right)\). Similarly, those defined at the boundary \(i+1/2\) have the subscript \(i+1\).
Note that the velocity \({u''}_{\text{k,i}}\) is stored as \(\text{UFCH} \left( I \right)\), and the velocity \({u'}_{\text{k,i}}\) used in the previous equations is calculated as:
(16.4-8)
where the coefficient \(\text{CCFU} \left( I \right)\) is defined by the Eq. 16.4-7 as:
(16.4-9)
The convective fluxes through the boundaries of the fuel region are set to zero, as no fuel is allowed to cross these boundaries in the LEMACO routine.
(16.4-10a)
(16.4-10b)
To preserve the accuracy of results in the boundary cells a correction is applied to the convective fluxes through all boundaries \(\text{IFFUBT}+1\) and \(\text{IFFUTP}\) whenever the corresponding interface (bottom and top) crosses that boundary during the time step. This correction is explained below for the case when the top fuel boundary crosses the cell boundary. The location of the interface at the end of the time step has already been calculated in the routine LEIF and is shown in Figure 16.4.12. The value of \(\left( {\rho'} u \right)_{\text{fu,IFFUTP}}\) is calculated according to Eq. 16.4-7 and then used in Eq. 16.4-5. The implicit assumption in Eq. 16.4-5 is that the value of the convective fluxes is constant over the length of the time step. However, as shown in Figure 16.4.12 the original location of the fuel interface was \(\text{FUIFTP}^{0} \left( 1 \right)\), and, before the interface reaches the cell boundary \(\text{ZC(IFFUTP)}\), the flux across the boundary is zero. The fraction of \(\Delta t\) during which the convective flux is present is:
(16.4-11)
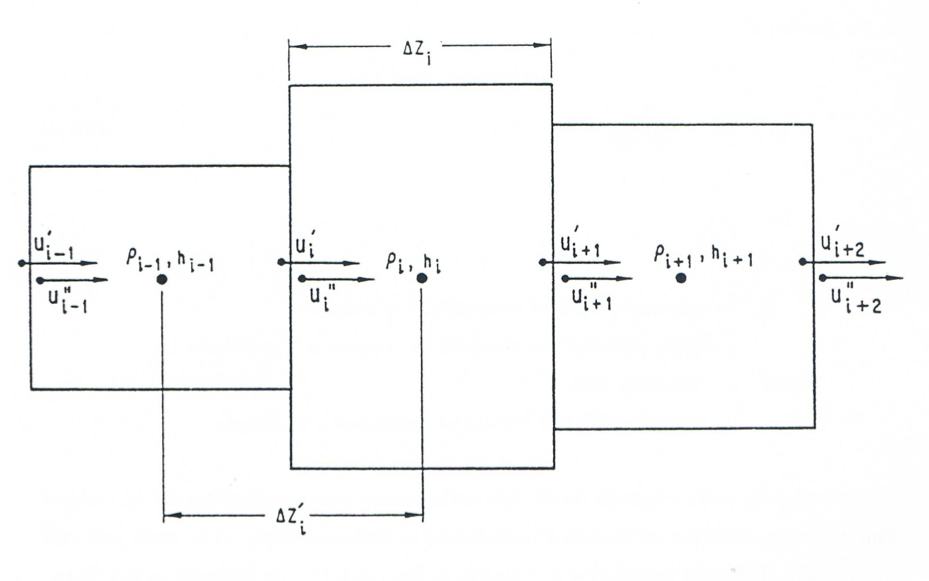
Figure 16.4.12 Figure 16.4.12: Correction for Material Boundary Crossing a Cell Boundary¶
In order to maintain the form of Eq. 16.4-5, rather than changing the value of \(\Delta t\) associated with \(\left( {\rho'} u \right)_{\text{fu,IFFUTP}}\) a corrected flux is defined, such that the product flux * time is correct:
(16.4-12)
A similar correction is applied for the bottom boundary.
Similar mass conservation equations are solved for all other LEVITATE components, i.e. molten steel, fuel and steel chunks, fission gas, sodium, steel vapor, fuel vapor, fission gas still present in the chunks and fission gas present in the molten fuel.
16.4.3.2. Liquid Fuel Energy Conservation Equations¶
The liquid fuel energy equation is solved in the routine LESOEN, for all cells in the molten fuel region, i.e., \(\text{IFFUBT} \leq I \leq \text{IFFUTP}\). We begin with the energy equation in conservation form:
(16.4-13)
where:
\(Q_{\text{fu,i}}\) = fission power source in cell \(i\) [J/(kg-s)]
\(A_{\text{fu,j,i}}\) = heat-transfer area between fuel and component \(j\) in cell \(i\) [m2]
After dividing by \(\text{AXMX} \cdot \Delta z_{\text{i}}\) and using the definition of generalized densities, we obtain:
(16.4-14)
where
(16.4-15)
Integrating over \(\Delta t\) and using the identity:
(16.4-16)
we obtain:
(16.4-17)
Finally, dividing Eq. 16.4-17 by \({\rho'}_{\text{fu,i}}^{n + 1}\) and expressing \(\Delta{\rho'}_{\text{fu,i}}\) as:
(16.4-18)
from the continuity Eq. 16.4-4, we obtain the change in the fuel enthalpy:
(16.4-19)
The new fuel enthalpy is obtained as:
(16.4-20)
The energy convective terms in Eq. 16.4-19 are calculated using an upstream differencing approach, i.e.;
(16.4-21)
These fluxes are based on the fuel densities, enthalpies and velocities at the of the time step. They are calculated in the routine LEMACO, before the calculation of the new densities, and stored in the array \(\text{COFUOS} \left( I \right)\). The sum of the heat-transfer contributions, \(\sum_{\text{j}}{{H'}_{\text{fu,j,i}} \cdot \Delta T_{\text{fu,j,i}}}\) is presented in detail in Eq. 16.4-22.
In the code, Eq. 16.4-19 is written as:
(16.4-22)
where
(16.4-23)
(16.4-24)
\(\text{HTFUNA} \left( I \right) = {H'}_{\text{fu,mi,i}}\) = generalized heat-transfer coefficient between fuel and gas mixture in cell \(i\)
\(\text{HTFUCL} \left( I \right) = {H'}_{\text{fu,cl,i}}\) = generalized heat-transfer coefficient between fuel and cladding in cell \(i\)
\(\text{HTFUFL} \left( I \right) = {H'}_{\text{fu,fl,i}}\) = generalized heat-transfer coefficient between fuel and fuel chunks in cell \(i\)
\(\text{HTFUSL} \left( I \right) = {H'}_{\text{fu,sl,i}}\) = generalized heat-transfer coefficient between fuel and steel chunks in cell \(i\)
\(\text{HTFUSR} \left( I \right) = {H'}_{\text{fu,sr,i}}\) = generalized heat-transfer coefficient between fuel and hexcan wall in cell \(i\)
\(\text{HTSEFU} \left( I \right) = {H'}_{\text{fu,se,i}}\) = generalized heat-transfer coefficient between fuel and molten steel in cell \(i\)
The generalized transfer coefficients \({H'}_{\text{fu,j,i}}\) are related to the heat-transfer coefficients \(H_{\text{fu,j,i}}\) and the transfer areas \(A_{\text{fu,j,i}}\) by Eq. 16.4-15. These transfer coefficients are calculated prior to the energy equation solution in the routine LETRAN (LEVITATE TRANSFER). Depending on the flow regime, some of those coefficients can be zero, as illustrated in the decision arrays Figure 16.4.3 through Figure 16.4.6.
After the energy change is calculated, and the new energy is obtained according to Eq. 16.4-20, the temperature of the fuel is calculated by using an external function, \(\text{TEFUEG}\), which uses the enthalpy as argument
(16.4-25)
Several checks are performed on the final temperature in order to avoid numerical difficulties. Thus, if only small amounts of fuel are present (fuel volume less than .1% of the cell volume) the temperature of the fuel is set equal to the cladding temperature or, if the fuel is surrounded by molten steel, to the molten steel temperature.
The condensation/vaporization energy sources/sinks are not included here. They will be introduced later in this chapter, when presenting the energy conservation calculation for fuel vapor.
16.4.3.3. Liquid Steel Energy Conservation Equation¶
The liquid steel energy equation is solved in the routine LESOEN, for all cells in the molten steel region, i.e. \(\text{IFSEBT} \leq I \leq \text{IFSETP}\). The energy conservation equation is similar to the molten fuel equation, but does not include a fission source term. Thus, the change in the steel enthalpy is:
(16.4-26)
The new steel enthalpy is obtained as:
(16.4-27)
The energy convective terms in Eq. 16.4-26 are calculated using an upstream differencing approach, similar to Eq. 16.4-19. They are calculated in routine \(\text{LEMACO}\) and stored under the name \(\text{COSEOS} \left( I \right)\). These fluxes are based on steel densities enthalpies and velocities at the beginning of the time step.
If \({u'}_{\text{se,i}} \geq 0\),
(16.4-28a)
If \({u'}_{\text{se,i}} < 0\), then
(16.4-28b)
As previously explained, the molten steel and molten fuel share the same velocity field. Thus \({u'}_{\text{se,i}}\) and \({u'}_{\text{fu,i}}\) have the same value, stored in the array \(\text{UFCH} \left( I \right)\).
In the code, Eq. 16.4-26 is written as:
(16.4-29)
where
(16.4-30)
(16.4-31)
\(\text{HTSEFU} \left( I \right) = {H'}_{\text{se,fu,i}}\) = transfer coefficient between steel and fuel in cell \(i\)
\(\text{HTSECL} \left( I \right) = {H'}_{\text{se,cl,i}}\) = transfer coefficient between steel and cladding in cell \(i\)
\(\text{HTSESR} \left( I \right) = {H'}_{\text{se,sr,i}}\) = transfer coefficient between steel and hexcan wall in cell \(i\)
\(\text{HTSEFL} \left( I \right) = {H'}_{\text{se,fl,i}}\) = transfer coefficient between steel and fuel chunks in cell \(i\)
\(\text{HTSESL} \left( I \right) = {H'}_{\text{se,sl,i}}\) = transfer coefficient between steel and steel chunks in cell \(i\)
\(\text{HTSENA} \left( I \right) = {H'}_{\text{se,mi,i}}\) = transfer coefficient between steel and gas mixture in cell \(i\)
The generalized heat-transfer coefficients are defined by:
(16.4-32)
and are described in detail in Section 16.4.3.10.
After the energy change is calculated, the new energy of the steel is calculated according to Eq. 16.4-27, and the temperature of the steel is obtained by using an external function, TESEEG, which uses the enthalpy as argument:
(16.4-33)
Several checks are performed during the steel temperature calculation in order to avoid numerical difficulties. Thus, if only small amounts of molten steel are present (steel volume less than .1% of the cell volume) the temperature of the steel is set equal to the cladding temperature or, if the steel is surrounded by molten fuel, to the molten fuel temperature.
The condensation/vaporization energy sources/sinks are not included here. They will be introduced later in this chapter, when the energy conservation calculation for steel vapor is presented.
16.4.3.4. Fuel and Steel Chunk Energy Conservation Equations¶
These equations are solved in the routine LESOEN. Separate equations are solved for the fuel and steel solid chunks, as described below.
16.4.3.4.1. The Energy Conservation Equation for the Fuel Chunks¶
The energy equation is written in conservative form as follows:
(16.4-34)
where
\(Q_{\text{fl,i}}\) = fission power source in the fuel in cell \(i\) [J/kg-s]
\(A_{\text{fl,i}}\) = area covered by chunks in cell \(i\), when imagined as a continuum with density \(\rho_{\text{fl}}\).
Following the same steps as outlined in Eq. 16.4-14 through 16.4-19, we obtain:
(16.4-35)
where
(16.4-36)
The energy convective terms in Eq. 16.4-35 are calculated using an upstream differencing approach, similar to that used for Eq. 16.4-21. The convective fluxes are calculated in the routine LEMACO, before the calculation of the new fuel chunk densities, and stored in the array \(\text{COLVOS} \left( I \right)\). The new fuel chunk enthalpy and temperature are then calculated:
(16.4-37)
(16.4-38)
16.4.3.4.2. The Energy Conservation for the Steel Chunks¶
This equation is very similar to the equation used for the fuel chunks, but the fission energy source is not present anymore. Only the final form of the equation is presented here:
(16.4-39)
where
(16.4-40)
The new steel chunk enthalpy and temperature are then calculated as follows:
(16.4-41)
(16.4-42)
16.4.3.5. Sodium and Fission-gas Energy Conservation Equation¶
The sodium and the fission gas are assumed in LEVITATE to be in equilibrium at the same temperature \(T_{\text{Na,i}}\). The sodium can exist in the form of superheated vapor or as a two-phase, vapor-liquid mixture. When required by the thermodynamic conditions the two-phase sodium component can become subcooled sodium. The two-phase sodium is assumed to be in thermodynamic equilibrium. The energy conservation equation is solved simultaneously for sodium and fission gas for all cells in the LEVITATE interaction region, i.e., \(\text{IFMIBT} \leq I \leq \text{IFMITP}\). Because the fission-gas region extends only between \(\text{IFFIBT} \leq I \leq \text{IFFITP}\), it is possible that some cells contain only sodium, without any fission gas. In these cells, the energy equation for the sodium-fission-gas mixture reduces to a sodium-only equation. Because significant differences exist between the behavior of superheated and two phase sodium, two separate equations are used.
16.4.3.5.1. The Energy Conservation Equation for Superheated Sodium and Fission Gas¶
The energy equation used for superheated sodium and fission gas is written in conservative form as:
(16.4-43)
where:
\(H_{\text{j,Mi,i}}\) = heat-transfer coefficient between component \(j\) and sodium-fission gas mixture in cell \(i\) [J/m2 - s- K]
\(A_{\text{j,Mi,i}}\) = heat-transfer area between component \(j\) and the gas mixture in cell \(i\) [m2]
\(\Delta T_{\text{j,Mi,I}}\) = temperature difference between component \(j\) and the gas mixture in cell \(i\) [K]
After dividing by \(\text{AXMX} \cdot \Delta z_{\text{i}}\) and using the definition of generalized densities, we obtain:
(16.4-44)
where the generalized heat-transfer coefficients are defined by:
(16.4-45)
and the sum of the heat-transfer terms \(\sum_{\text{j}}{{H'}_{\text{j,Mi,i}} \cdot \Delta T_{\text{j,Mi,i}}}\) is presented in Eq. 16.4-54. Integrating over \(\Delta t\) and using the identity shown in Eq. 16.4-16 to express the quantity \(\Delta \left( {\rho'} h \right)\), we obtain:
(16.4-46)
Two sets of equation relating the thermodynamic characteristics of a gas are used to refine Eq. 16.4-46. These are:
(16.4-47a)
(16.4-47b)
and
(16.4-48a)
(16.4-48b)
where the constant \(R_{\text{j}}\) is defined as:
(16.4-49)
with
\(R\) = universal gas constant [J/mol - K]
\(M_{\text{j}}\) = molar mass of gas \(j\) [kg/mol]
\(T_{\text{sat}} = T_{\text{sat}} \left( P_{\text{Na,i}} \right)\) ; \(h_{\text{Na,vap}} = h_{\text{Na,vap}} \left( P_{\text{Na,i}} \right)\).
With \(T_{\text{Na,i}} = T_{\text{fi,i}}\) and \(\theta_{\text{Na,i}} = \theta_{\text{fi,i}} = \theta_{\text{Mi,i}}\) , after expressing the quantity \(\Delta T_{\text{j,Mi,i}}\) as:
(16.4-50)
and differencing Eqs. 16.4-47a and 16.4-47b to obtain \(\Delta h_{\text{Na,i}}\) and \(\Delta h_{\text{fi,i}}\), Eq. 16.4-46 becomes:
(16.4-51)
After using the identity:
(16.4-51a)
and replacing \(\Delta {\rho'}_{\text{Na,i}}\) and \(\Delta {\rho'}_{\text{fi,i}}\) by using the continuity equation, Eq. 16.4-51 becomes:
(16.4-52)
The terms derived from the original \(\frac{\partial \text{P}}{\partial \text{t}}\) and, \(u \cdot \frac{\partial \text{P}}{\partial \text{z}}\) terms in Eq. 16.4-43 make a negligible contribution to the right hand side of Eq. 16.4-42. The terms are neglected in the initial release version, but have been added, for completeness, in the chunk development version. The left-hand-side coefficient is replaced by:
(16.4-53)
After dividing Eq. 16.4-52 by AUXLR, the new mixture temperature is calculated as follows:
(16.4-54)
where:
(16.4-55)
(16.4-56)
\(\text{HTNACL} \left( I \right) = {H'}_{\text{cl,Na,i}}\) = transfer coefficient between cladding and mixture in cell \(i\)
\(\text{HTSENA} \left( I \right) = {H'}_{\text{se,Na,i}}\) = transfer coefficient between steel and gas mixture in cell \(i\)
\(\text{HTNASR} \left( I \right) = {H'}_{\text{sr,Na,i}}\) = transfer coefficient between hexcan wall and gas mixture in cell \(i\)
\(\text{HTFUNA} \left( I \right) = {H'}_{\text{fu,Na,i}}\) = transfer coefficient between molten fuel and gas mixture in cell \(i\)
\(\text{HTNAFL} \left( I \right) = {H'}_{\text{fl,Na,i}}\) = transfer coefficient between steel chunks and mixture in cell \(i\)
\(\text{HTFCNA} = {H'}_{\text{ffc,Na,i}}\) = transfer coefficient between frozen fuel on cladding and gas mixture in cell \(i\)
\(\text{HTFSNA} = {H'}_{\text{ffs,Na,i}}\) = transfer coefficient between frozen fuel on can wall and gas mixture in cell \(i\)
The convective enthalpy fluxes used in Eq. 16.4-53 are calculated using an upstream differencing approach:
If \({u'}_{\text{Na,i}} \geq 0\)
(16.4-57)
If \({u'}_{\text{Na,i}} < 0\)
(16.4-58)
The enthalpy \(h_{\text{Na,i}}\) is calculated as follows
If \(X_{\text{Na,i}} \geq 1\) (single-phase sodium vapor),
(16.4-58a)
If \(0 \leq X < 1\) (two-phase sodium), then
(16.4-58b)
where
\(h_{\text{Na,fg}} \left( T_{\text{Na,i}} \right)\) = the heat of vaporization of sodium at the temperature \(T_{\text{Na,i}}\)
\(h_{\text{Na,liq}} \left( T_{\text{Na,i}} \right)\) = enthalpy of liquid sodium on the saturation curve at \(T_{\text{Na,i}}\)
\(h_{\text{Na,vap}} \left( P_{\text{Na,i}} \right)\) = enthalpy of sodium vapor on the saturation curve at pressure \(P_{\text{Na,i}}\)
If injection of fission gas has taken place in the previous time step, a correction of the temperature is made to account for the enthalpy of the injected gas. When the injection is calculated, this gas is assumed to be at the same temperature as the sodium-fission gas mixture in the channel in order to avoid recalculating the mixture temperature.
(16.4-59)
The pressure of the mixture is then calculated as:
(16.4-60)
where \(P_{\text{Na,i}}\) and \(P_{\text{fi,i}}\) are calculated using Eqs. 16.4-48a and 16.4-48b. In using this equation for sodium, it is recognized that in the neighborhood of the saturation curve the behavior of the sodium vapor will deviate from the perfect-gas behavior. Thus, the constant \(R_{\text{Na,i}}\) is allowed to vary so that the pressure calculated by Eq. 16.4-48a will match the saturation pressure when the mixture is right on the saturation curve. The parameter used to decide if this procedure is necessary is the ratio:
(16.4-61)
where
\(\rho_{\text{Na,i}}\) = physical density of the sodium vapor
\(\rho_{\text{Na,vap}}\) = physical density of the saturated sodium vapor
If \(r_{\text{i}} < r_{\text{min}}\) the sodium vapor is far enough from saturation and the perfect-gas law is satisfactory. Otherwise, the constant \({R'}_{\text{Na,i}}\) is defined as:
(16.4-62)
where
(16.4-63)
and \(r_{\text{min}}\) is the ratio obtained from the sodium thermodynamic properties tables for a wide range of interest; currently \(r_{\text{min}} = .067\).
This derivation assumes that the sodium is in the superheated vapor region for the entire duration of the time step \(\Delta t\). Occasionally, however, the sodium vapor might become saturated and this assumption would no longer hold. In the two-phase region the temperature changes are smaller than those in the single-phase region, since much of the energy lost will lead to condensation, rather than to a change in temperature. Thus, where necessary, a correction is performed which reduces the temperature drop in the two-phase region by bringing the final sodium temperature close to the saturation curve. The correction is considered necessary whenever the following condition is satisfied:
(16.4-64)
where \(\Delta P_{\text{constant}}\) is a built-in constant, currently set to \(0.05 \cdot 10^{5}\) Pa. This procedure is illustrated in Figure 16.4.13. The corrected sodium temperature is calculated as follows:
(16.4-65)
where
\(T_{\text{o}}\) = sodium temperature at the beginning of the time step
\(T_{1}\) = calculated new sodium temperature, from Eq. 16.4-59
\(\Delta P_{\text{o}}, \Delta P_{1} = P_{\text{Na,sat,i}} - P_{\text{Na,i}}\) at the beginning and end of time step, respectively.
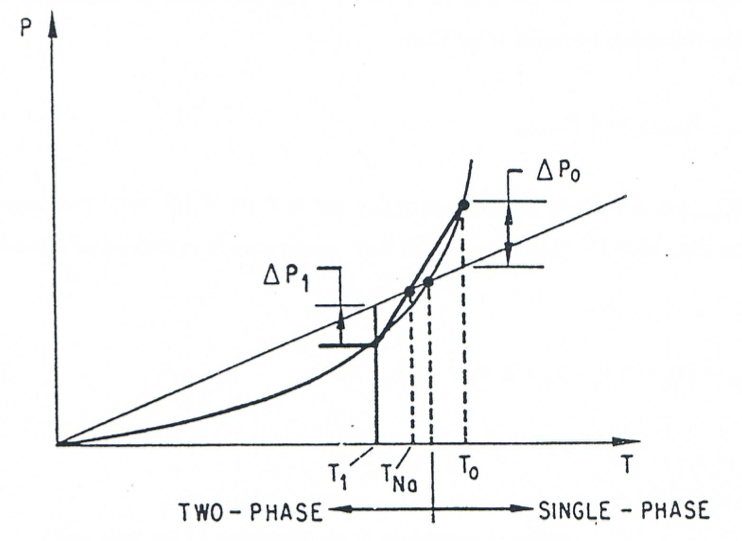
Figure 16.4.13 Correction for Sodium Vapor Transition to a Two-phase Mixture¶
16.4.3.5.2. The Energy Equation for Two-phase Sodium and Fission Gas¶
The same considerations as before are made to arrive at the Eq. 16.4-46, but the compressible term, \(\theta \frac{\partial \text{P}}{\partial \text{t}}\), is not included for the two-phase component. To express the quantity \(\Delta h_{\text{Na,i}}\), we use the identity:
(16.4-66)
Thus:
(16.4-67)
Using the definitions:
(16.4-68a)
(16.4-68b)
(16.4-68c)
(16.4-68d)
Eq. 16.4-66 becomes:
(16.4-69)
By substituting:
(16.4-70)
in Eq. 16.4-69, we obtain:
(16.4-71)
Finally, substituting Eq. 16.4-71 into 16.4-46 and keeping the terms containing \(\Delta T\) on the left-hand side, we have:
(16.4-72)
We now rewrite:
(16.4-73)
(16.4-74)
(16.4-75)
and, after some regrouping following the same procedure as in the case in the single-phase sodium, we obtain:
(16.4-76)
where
(16.4-77)
(16.4-78)
(16.4-79)
The heat-transfer coefficients are the same as those used in the single-phase energy equation. The pressure of the mixture is then calculated as follows:
(16.4-80)
where
(16.4-81)
(16.4-82)
However, if significant amounts of liquid sodium are present (more than 30% of the volume fraction), the compressibility of the liquid sodium is taken into account in calculating the partial fission-gas pressure. Eq. 16.4-82 is written in the form:
(16.4-83)
where
(16.4-84)
The value of \(C_{\Delta \text{P,Na}}\) is given by the input constant CMNL. By solving Eq. 16.4-83 and retaining only the positive root, we obtain:
(16.4-85)
16.4.3.6. Fuel Vapor Energy Conservation Equation¶
The fuel vapor energy conservation equation is solved in the routine LEFUVA, which also models the fuel vaporization/condensation processes. These processes are not included in the formulation of the liquid fuel energy conservation equation, which is solved in the LESOEN routine. Thus, the mass and temperature of the liquid fuel is corrected in the routine LEFUVA, when necessary, to account for the mass and energy sources/sinks due to condensation and vaporization. Because the fuel vapor effects become dominant only during high-power transients that are associated with very short time periods, the fuel vapor is assumed not to be in equilibrium with the liquid fuel. The treatment of the vaporization and condensation processes will be described in detail later in this chapter.
16.4.3.6.1. Energy Conservation for Superheated Fuel Vapor¶
First, the energy equation is solved by assuming that all fuel vapor is initially superheated. This assumption is consistent with the method of solution, as all condensation and vaporization events are calculated in the routine LEFUVA, and the fuel vapor remaining in each cell at the end of this routine is always superheated, or, in the limit, saturated dry. Condensation or vaporization effects that might occur during the current time step are ignored during this first step. The energy equation is written in conservative form:
(16.4-86)
After dividing by \(\text{AXMX} \cdot \Delta z_{\text{i}}\) and using the definition of generalized densities, we obtain:
(16.4-87)
Integrating over \(\Delta t\) and using the identity in Eq. 16.4-16 to express the quantity \(\Delta \left( {\rho'} h \right)\), we obtain:
(16.4-88)
The fuel vapor is only present in calculations for short periods of time during high overpower transients. In addition, the gas-gas heat transfer is generally much more efficient than the gas-liquid or gas-surface heat transfer. For these reasons the only heat-transfer term maintained in Eq. 16.4-86 is the heat transfer between the fuel vapor and the sodium-fission gas mixture. Furthermore, because of the lack of experimental data on the gas-gas heat transfer, this term has been formulated such that it represents a sizable fraction of the transferable energy, i.e., the temperatures of the fuel vapor and gas mixture will equilibrate quite fast, within 10-50 time steps. The enthalpy of the fuel vapor at a certain temperature is:
(16.4-89)
A measure of the transferable enthalpy is obtained by assuming the lowest final temperature to be the temperature of the sodium-fission gas mixture. Thus:
(16.4-90)
The total transferable enthalpy in cell \(i\), during the time \(\Delta t\) is:
(16.4-91)
The fraction transferred is \(\text{CFHTAX}\), which is defined as follows:
When \(\Delta t \cdot 10^{3} \leq 0.1\)
(16.4-92a)
When \(\Delta t \cdot 10^{3} > 0.1\)
(16.4-92b)
After multiplying by \(\text{CFHTAX}\) and dividing by \(\text{AXMX} \cdot \Delta z_{\text{i}}\), which was done for the original equation, the heat-transfer term in Eq. 16.4-88 is replaced by:
(16.4-93)
Substituting Eq. 16.4-93 in Eq. 16.4-88 and rewriting the \(\theta_{\text{Mi,i}} \cdot \Delta P_{\text{fv,i}}\) and \(\rho_{\text{fv,i}}^{n + 1}\) terms in a manner similar to that used for the sodium-gas mixture, in Eqs. 16.4-47 through 16.4-51, we obtain:
(16.4-94)
The terms derived from the original \(\frac{\partial \text{P}}{\partial \text{t}}\) and \(\frac{\partial \text{P}}{\partial \text{z}}\) terms in Eq. 16.4-86 make a negligible contribution to the right hand side of Eq. 16.4-94. These terms were neglected in the initial release version, but have been added for completeness, in the chunk development version. The left-hand-side coefficient is replaced by:
(16.4-95)
The terms in Eq. 16.4-95 have not been combined because the term \({\rho'}_{\text{fv,i}}^{n + 1} \cdot R_{\text{fv}}\) originates from the \(\frac{\partial \text{P}}{\partial \text{t}}\) term and was dropped in the initial release version, together with the terms originating from the u \(\frac{\partial \text{P}}{\partial \text{u}}\) term. The new fuel vapor temperature is calculated as follows:
(16.4-96)
where
(16.4-97)
(16.4-98)
and
(16.4-99)
(16.4-100)
The new fuel vapor pressure is then calculated using the new temperatures:
(16.4-101)
16.4.3.6.2. Condensation of the Fuel Vapor¶
Under certain circumstances the fuel vapor will enter the two-phase region and begin to condense. The decision that such a situation has occurred is made by comparing the pressure \(P_{\text{fv,i}}^{n + 1}\) with the saturation pressure in cell \(i\). If:
(16.4-102)
no condensation will occur during the current time step. Otherwise, some condensation will take place, and the calculation proceeds as outlined below.
First, we determine the temperature \(T_{\text{fv,sat,i}}\) where the fuel vapor first reaches saturation. This temperature is obtained using the same method described in Section 16.4.3.5 to correct the sodium temperature where it crosses over from the single phase to the two-phase region. The formula used is similar to Eq. 16.4-65. The enthalpy change between the original temperature \(T_{\text{fv,i}}^{n}\) and the saturation temperature is, by Eq. 16.4-94:
(16.4-103)
The total enthalpy change originally calculated is:
(16.4-104)
The enthalpy which still has to be removed via condensation once the vapor has reached the temperature \(T_{\text{fv,sat,i}}\) is given by:
(16.4-105)
In order to find the temperature change leading to the enthalpy change \(\Delta h_{\text{fv,i}}^{\text{cond}}\), we observe that at the final temperature we have to satisfy the condition for dry vapor:
(16.4-106)
Also, with the assumption that the heat of vaporization for fuel \(h_{\text{fv,lg}}\) is approximately constant for the range of temperatures of interest, the total enthalpy change due to condensation and temperature change can be written as:
(16.4-107)
where \(\Delta {\rho'}_{\text{fv,i}}\) is the decrease in generalized density due to condensation. Because Eqs. 16.4-106 and (16.4-107) cannot be solved directly for the temperature, we use a trial and error approach to find the solution. First, assuming the final temperature if \(T_{\text{fv}}^{1} = T_{\text{fv,i}}^{n + 1}\), i.e., the temperature originally calculated, and the amount to condense \(\Delta {\rho'}_{\text{fv}}^{1}\), Eq. 16.4-106 becomes:
(16.4-108)
and, after solving for \(\Delta {\rho'}_{\text{fv}}\):
(16.4-109)
The enthalpy change in Eq. 16.4-107 becomes:
(16.4-110a)
Then, we assume that the final temperature of the fuel vapor is \(T_{\text{fv}}^{2} = T_{\text{fv,sat}}\), and obtain the new amount of condensate \(\Delta {\rho'}_{\text{fv}}^{2}\) and the energy change:
(16.4-110b)
These two situations generally will bracket the actual final temperature of the fuel vapor, because the first assumption is practically equivalent to very little or no condensation, while the second assumes maximum condensation with no temperature change. The actual temperature is obtained by interpolating between \(T_{\text{fv}}^{1}\) and \(T_{\text{fv}}^{2}\), with the condition that the final enthalpy change has to be \(\Delta h_{\text{fv,i}}^{\text{cond}}\), calculated before from Eq. 16.4-105. Thus:
(16.4-111)
Using this temperature, the actual condensation is calculated from Eq. 16.4-109 and the generalized density of the fuel vapor is updated:
(16.4-112)
The temperature and generalized density of the liquid fuel is also modified to account for the addition of \(\Delta {\rho'}_{\text{fv,i}}^{\text{cond}}\) at the temperature \(T_{\text{fv,i}}^{n + 1}\):
(16.4-113)
(16.4-114)
16.4.3.6.3. Vaporization of Liquid Fuel¶
The vaporization model used is a quasi-equilibrium model [16-13] which allows the fuel and fuel vapor to have different temperatures at the same location. Bulk boiling of fuel is assumed to occur whenever the local total pressure is lower than the vapor pressure of the liquid fuel. This process is fast enough to allow a quasi-equilibrium to be established each time step, and is illustrated in Figure 16.4.14 by the original sharp increase in pressure. Thus, the total pressure, including the partial pressure of the fuel vapor becomes equal to the fuel vapor pressure corresponding to the liquid-fuel temperature. When the total pressure exceeds the liquid-fuel vapor pressure, fuel vaporization can occur only by surface vaporization, which is generally a significantly slower process than bulk boiling. The efficiency of surface vaporization is a function of the local flow regime and time-step length. In the limit, if the surface vaporization is assumed to be very efficient, the partial pressure of the fuel vapor can become equal, in each time step, to the liquid-fuel pressure. In this case, the quasi-equilibrium model becomes equivalent to a thermal-equilibrium model.
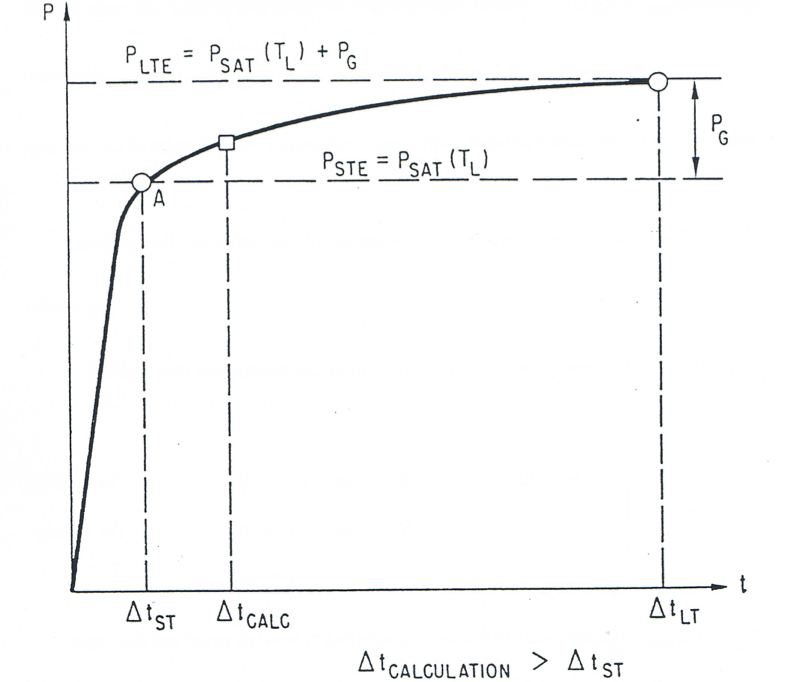
Figure 16.4.14 Time Variation of Fuel Vapor Partial Pressure¶
This calculation is performed for all cells \(I\), with \(\text{IFFUBT} < I < \text{IFFUTP}\). First, we calculate \(P_{\text{fu,sat,i}} = P_{\text{sat}} \left( T_{\text{fu,i}} \right)\). Further vaporization of the liquid fuel in cell I will occur only if:
(16.4-115)
where \(C_{\text{Pr,fu}}\) is a coefficient dependent on the local configuration and the length of the time step as follows:
If the fuel is the continuous component, i.e., in the annular or bubbly fuel flow regimes
(16.4-116a)
If the fuel is in the form of droplets, i.e. in the annular and bubbly steel flow regimes,
(16.4-116b-c)
The case \(C_{\text{Pr,fu}} = 0\) corresponds to full thermal equilibrium between liquid and fuel vapor.
The vaporization of liquid fuel will take place until the following condition is satisfied:
(16.4-117)
Note that all pressures change during vaporization, including \(P_{\text{fu,sat,i}}\). Thus, Eq. 16.4-117 cannot be solved directly, and we need to use a trial-and-error approach. First, it is assumed that the final fuel temperature is:
(16.4-118)
and
(16.4-119)
We can now calculate the amount of new fuel vapor generated from Eq. 16.4-117:
(16.4-120)
The new fuel enthalpy is:
(16.4-121)
and the new fuel temperature and vapor pressure are:
(16.4-122)
(16.4-123)
A new guess is now made about the final fuel temperature \(T_{\text{fu,i}}^{2} = {T'}_{\text{fu,i}}\), and the above procedure is repeated, obtaining \(P_{\text{fu,sat,i}}^{2}\), \(\Delta {\rho''}_{\text{fu,i}}\), \({T''}_{\text{fu,i}}\) and \({P''}_{\text{fu,sat,i}}\). We can now obtain the real \(P_{\text{fu,sat,i}}\), by imposing the condition that the final saturation pressure should be equal to the assumed saturation pressure:
(16.4-124)
where
(16.4-125a)
(16.4-125b)
Using \(P_{\text{fu,sat,i}}^{n + 1}\) in Eq. 16.4-120, we can calculate the new \(\Delta {\rho'}_{\text{fv,i}}\). Then, the generalized densities and enthalpies of the fuel vapor and liquid fuel are updated:
(16.4-126)
(16.4-127)
(16.4-128)
(16.4-129)
Finally, the new pressure due to fuel vapor is calculated:
(16.4-130)
and is added to the total channel pressure:
(16.4-131)
16.4.3.7. Steel Vapor Energy Conservation Equation¶
The steel vapor energy conservation equation is solved in the routine LESEVA. This routine is practically identical to the LEFUVA routine, which solves the fuel vapor energy equation and was described in detail in Section 16.4.3.6. At the end of the LESEVA routine, the new pressure due to steel vapor is calculated
(16.4-132)
and is added to the total channel pressure:
(16.4-133)
16.4.3.8. Momentum Conservation Equation¶
The momentum conservation equations are solved in the routine LEMOCO. As indicated previously, the channel hydrodynamic model in LEVITATE calculates three velocity fields, each of them describing the motion of a group of material components, as follows:
\(u'_{Mi,i}, u''_{Mi,i}\) |
the velocity of the gas mixture; described the motion of the two-phase (or superheated) sodium, fission gas, fuel vapor and steel vapor. The code symbol is UMCH. |
|---|---|
\(u'_{fu,i}, u''_{fu,i}\) |
the velocity of the liquid fuel and/or liquid steel components. The code symbol is UFCH. |
\(u_{lu,i}\) |
the velocity of the solid fuel and/or steel chunks. The code symbol is ULCH. |
One is reminded that LEVITATE uses dual velocities to model the motion of the gas mixture and liquid components. Thus, \({u'}_{\text{Mi,i}}\) represents the velocity of the gas mixture before the \(i-1/2\) boundary and \({u''}_{\text{Mi,i}}\) represents the velocity of the mixture after the same boundary. (Before and after velocities are ordered here by the positive sense of the axial coordinate). As already shown in Section 16.4.3.1, the dual velocities at the boundary \(i-1/2\) are related by:
(16.4-134)
In the code, only the velocity \({u''}_{\text{fu,i}}\) is stored in the array \(\text{UFCH} \left( I \right)\). The velocity \({u'}_{\text{fu,i}}\) is always obtained from Eq. 16.4-134, using the coefficient \(C_{\text{Mo,fu,i}}\), which is stored in the array \(\text{CCFU} \left( I \right)\). A similar approach is used for the gas mixture dual velocities, which are related at the boundary \(i-1/2\) by the coefficients \(C_{\text{Mo,Mi,i}}\), stored in the array \(\text{CCMI} \left( I \right)\).
The three momentum equations are solved simultaneously to avoid numerical instabilities due to the generally low inertia of the gas mixture. In cells where only two velocity fields are necessary (e.g., no fuel/steel chunks are present) a system of only two momentum equations is solved. Finally, in cells where the gas mixture only is present, the corresponding momentum equation is solved, while the other two velocity fields remain zero. We first present the derivation of the momentum equations.
16.4.3.8.1. The Momentum Conservation Equation for the Gas Mixture¶
We begin with the equation written in conservative form for the control volume illustrated in Figure 16.4.15:
(16.4-135)
where \(\sum{\Gamma_{\text{Mo,i-1}}^{l}}\) represents the momentum sources and sinks for the mixture and will be presented in detail later in this chapter. We now divide Eq. 16.4-135 by \(\text{AXMX}\) and using the definition of the generalized density, the notation:
(16.4-136)
and the correlation of \({u'}_{\text{Mi,i}}\) and \({u''}_{\text{Mi,i}}\), obtain
(16.4-137)
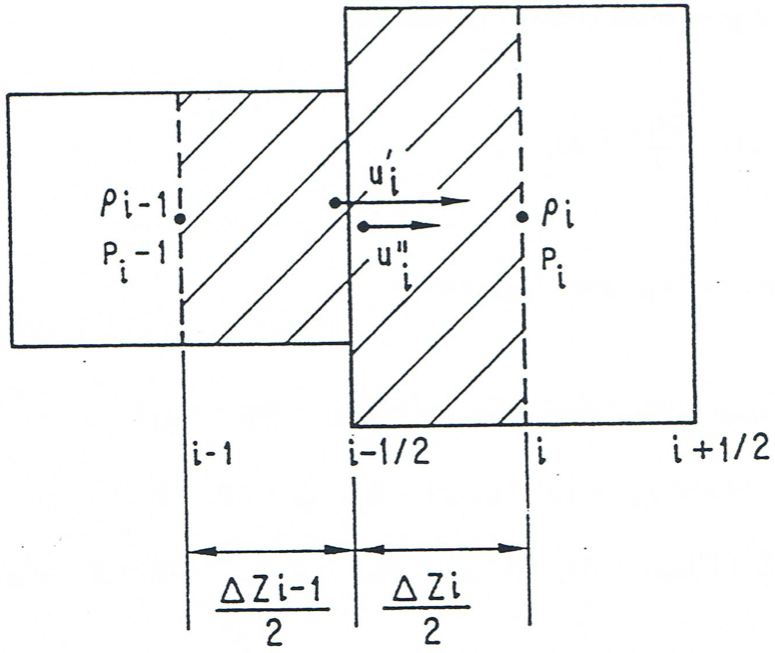
Figure 16.4.15 Control Volume Used for the Solution of the Momentum Equation¶
where we used
(16.4-138)
in order to simplify the notation and:
(16.4-139)
The convective fluxes in Eq. 16.4-137 are defined as follows:
(16.4-140)
An optional formulation of the convective fluxes can be obtained by setting the input parameter \(\text{IMOMEN} = 1\), in which case:
(16.4-141)
where
(16.4-142a-d)
This option has been added only recently and has not been tested extensively. It is expected that in future release versions this formulation will become the basic option. The quantity \(\theta_{\text{Mi,i-1/2}}\) is defined differently for expansions and contractions [16-5]. For an expansion:
(16.4-143a-b)
and for contraction:
(16.4-144)
with \(C_{\Delta \text{p}}\) currently having the value of 1.67. Equation 16.4-137 is integrated over the time interval and then divided by \(\Delta t\). Using the identities:
(16.4-145a)
(16.4-145b)
we obtain:
(16.4-146)
We will now present the term \(\sum_{l}{{\Gamma'}_{\text{Mo,i}}^{l}}\) in more detail:
(16.4-147)
The momentum sink \({\Gamma'}_{\text{Mo,Mi,i}}^{\text{cond}}\) is due to possible condensation of steel and/or fuel vapor:
(16.4-148)
Similarly, the vaporization source is defined as:
(16.4-149)
The quantities \(\Delta {\rho'}_{\text{fv}}^{\text{cond}}\) and \(\Delta {\rho'}_{\text{fv}}^{\text{vap}}\) are calculated in the routine \(\text{LEFUVA}\). These calculations are presented in Section 16.4.3.6. The quantities \(\Delta {\rho'}_{\text{sv}}^{\text{cond}}\) and \(\Delta {\rho'}_{\text{sv}}^{\text{vap}}\) are obtained in the \(\text{LESEVA}\) routine in the same manner.
The momentum sink due to the wall friction has the form:
(16.4-150)
The wall friction factor \(f_{\text{Mi,i}}\) will be described in Section 16.4.3.10. The hydraulic diameter of the gas mixture \(D_{\text{H,Mi,i}}\) will be described in Section 16.4.3.9. The fuel/steel-gas mixture drag source has the form
(16.4-151)
The drag coefficient between fuel and mixture has different forms, depending on the local flow regime, as shown below:
For the annular fuel and steel flow regimes:
(16.4-152a)
(16.4-152b)
For the bubbly fuel flow regime:
(16.4-153a)
where CIA6 is an input constant, currently equal to 0.107. This form of \({C'}_{\text{D,Mi,fu,i}}\) is explained in more detail in Ch. 14.0, Section 14.4.6.1, which describes the PLUTO2 model.
For the bubbly steel flow regime:
(16.4-153b)
The factor \(f_{\text{Mi,fu,i}}\) which appears in Eq. 16.4-152a will be described in Section 16.4.3.10.
The chunk-mixture drag source has the form:
(16.4-154)
The drag coefficient \({C'}_{\text{D,Mi,lu,i}}\) is defined as follows:
For the annular steel or fuel flow regime:
(16.4-155)
where CIA4 and CIA5 are input constants, with the values 0.375 and -2.7, respectively. The coefficient \(C_{\text{DRAG}}\) is defined as follows:
If \(\text{Re}_{\text{lu,i}} > 500\),
(16.4-156a)
If \(\text{Re}_{\text{lu,i}} \leq 500\), then
(16.4-156b)
The chunk Reynolds number \(\text{Re}_{\text{lu,i}}\) used in Eq. 16.4-156 is defined as follows:
(16.4-157)
The coefficient \(C_{\text{AREA,Mi,} l \text{u,i}}\) is used to take into account the fact that the chunks are in contact not only with the gas mixture, but with other components too, such as molten fuel or steel and cladding. This coefficient will be described in Section 16.4.3.10.
For the bubbly steel and fuel flow regimes:
(16.4-158)
Finally, the inertial (or apparent mass) momentum source term has the form:
(16.4-159)
where
(16.4-160)
and the generalized inertial coefficient is defined as follows:
For annular steel or fuel flow, no inertial effects are present:
(16.4-161)
For bubbly steel flow:
(16.4-162)
For bubbly fuel flow:
(16.4-163)
The source terms \(\sum{{\Gamma'}_{\text{Mo,i-1}}^{l}}\) in Eq. 16.4-147 are similar to the \(\sum{{\Gamma'}_{\text{Mo,i}}^{l}}\) terms that have been presented in detail, but they cannot be obtained from \({\Gamma'}_{\text{Mo,i}}^{\mathcal{l}}\) by simply replacing the subscript \(i\) by \(i-1\). The velocity \(u_{\text{Mi,i}}\) in these terms has to be replaced by \({u'}_{\text{Mi,i}}\), i.e., \(C_{\text{Mo,Mi,i}} \cdot u_{\text{Mi,i}}\). The components of \(\sum{{\Gamma'}_{\text{Mo,i-1}}^{l}}\) are presented below:
(16.4-164)
(16.4-165)
(16.4-166)
(16.4-167)
(16.4-168)
(16.4-169)
where the definition of \(\frac{\Delta\left( u_{\text{fu}} - u_{\text{Mi}} \right)}{\Delta z}\) is the same as Eq. 16.4-160. It should be noted that, in the definition of the source terms, we used the assumption that changes in the coefficients \(C_{\text{Mo,fu,i}}\) can be neglected during one time step, and thus only the new coefficients at time \(n+1\) have been used.
We can now replace the expression \(\sum_{l}{\left( {\Gamma'}_{\text{Mo,i-1}}^{l} \cdot \Delta z_{\text{i}} + {\Gamma'}_{\text{Mo,i}}^{l} \cdot \Delta z_{2} \right)}\) in Eq. 16.4-147 using Eqs. 16.4-148 through 16.4-167. We then rearrange Eq. 16.4-147 in the form:
(16.4-170)
All terms containing the time change of the gas mixture velocity \(\Delta u_{\text{Mi,i}}\) were moved to the left-hand side of the Eq. 16.4-170, and after factoring \(\Delta u_{\text{Mi,i}}\), put in the form \(\text{DMX} \cdot \Delta u_{\text{Mi,i}}\). Similarly, all terms containing \(\Delta u_{\text{fu,i}}\) and \(\Delta u_{l \text{u,i}}\) were grouped together on the right-hand side. All other terms were grouped under the coefficient \(\text{AMX}\). It should be observed that the term \(\frac{\Delta\left( u_{\text{fu}} - u_{\text{Mi}} \right)}{\Delta z}\) which appears in Eqs. 16.4-159 and 16.4-169 does not contain time changes and thus will be included in the \(\text{AMX}\) coefficient.
16.4.3.8.2. The Momentum Conservation Equation for the Molten Fuel/Steel Component¶
Using an integration procedure similar to that used for the gas-mixture equation, we obtain the following equation:
(16.4-171)
where
(16.4-172)
The optional formulation, which can be obtained using \(\text{IMOMEN} = 1\) is:
(16.4-173)
where
(16.4-174a-d)
The quantity \(\theta_{\text{fu,i-1/2}}\) is defined by Eqs. 16.4-142 and 16.4-143, where the \(\theta_{\text{Mi,i}}\) is replaced by \(\left( \theta_{\text{fu,i}} + \theta_{\text{se,i}} \right)\). The source/sink terms in \(\sum_{\text{m}}{{\Gamma'}_{\text{Mo,fu,i}}^{m}}\) are defined in detail below:
The condensation term:
(16.4-175)
The vaporization term:
(16.4-176)
The wall friction term is dependent on the flow regime:
For the annular or bubbly fuel flow regimes:
(16.4-177)
For the annular or bubbly fuel flow regimes:
(16.4-178)
where
the \(D_{\text{H,se,i}}\) and \(D_{\text{H,fu,i}}\) are the hydraulic diameters for steel and fuel, respectively, and are described in Section 16.4.3.9.
the contact coefficients \(C_{\text{AREA,se,i}}\) and \(C_{\text{AREA,fu,i}}\) account for the fact that only a fraction of the steel or fuel perimeter is in contact with the stationary walls; they are described in Section 16.4.3.10; and the friction coefficients \(f_{\text{se,i}}\) and \(f_{\text{fu,i}}\) are defined below:
(16.4-179a-b)
(16.4-179c-d)
where \(\text{CIFRFU}\) and \(\text{CIREFU}\) are input constants. Currently, \(\text{CIFRFU} = .03\) and \(\text{CIREFU} = 2100\).
The fuel/steel-gas mixture drag source is similar, but of opposite sign, to the term already presented for the gas mixture.
(16.4-180)
The drag coefficient \({C'}_{\text{D,Mi,fu,i}}\) is defined by Eqs. 16.4-152 and 16.4-153.
The fuel/steel - chunk drag source is defined as follows:
(16.4-181)
The generalized drag coefficient \({C'}_{\text{D,fu,}l \text{u,i}}\) is flow regime dependent and is defined below:
For the steel annular and bubbly flow regimes:
(16.4-182)
For the fuel annular and bubbly flow regimes:
(16.4-183)
In the above equations, the drag coefficient \(C_{\text{DRAG}}\) is defined by 16.4-156. The area coefficients, which account for the fact that only a fraction of the chunk lateral area is in contact with the molten fuel or steel, are defined below:
(16.4-184)
where \(C_{\text{AREA,Mi,}l \text{u,i}}\) indicates the fraction of the lateral chunk area in contact with the gas mixture. The quantity \(1 - C_{\text{AREA,Mi,} l \text{u,i}}\) thus represents the fraction of the chunk area in contact with the molten fuel/steel and cladding/hexcan wall. The coefficient \(C_{\text{AREA,se,cl}}\) represents the fraction of the cladding/hexcan wall area covered by molten steel/fuel. Both these area coefficients will be explained in more detail in Section 16.4.3.9.
The momentum source due to fuel injection from the pin
(16.4-185)
The quantity \(\Delta {\rho'}_{\text{fu,injection,i}}\) represents the change in the fuel generalized density due to injection via the pin rip or via the end of the pin stubs, as explained in Section 16.3. The velocity of the injected material is \(u_{\text{fu,ca,i}}\), which is also explained in Section 16.3. The coefficient \(C_{\text{Mo,injection,i}}\) accounts for the axial momentum loss due to lateral acceleration and mixing during the injection process, and is defined as follows:
(16.4-186a-b)
where \(\text{CIFUMO}\) is an input constant, with values between 0 and 1.
To summarize, the term \(\sum_{\text{m}}{{\Gamma'}_{\text{Mo,fu,i}}^{m}}\), which appears in Eq. 16.4-171, has the form,
(16.4-187)
The term \(\sum_{\text{m}}{{\Gamma'}_{\text{Mo,fu,i-1}}^{m}}\) has a similar composition, and its terms are presented below:
(16.4-188)
(16.4-189)
For the steel flow regimes,
(16.4-190a)
For the fuel flow regimes:
(16.4-190b)
(16.4-191)
(16.4-192)
(16.4-193)
The source terms, as given by Eqs. 16.4-175 through 16.4-193 are substituted in Eq. 16.4-171, and, after rearranging, the fuel momentum equation is written in the form
(16.4-194)
16.4.3.8.3. The Momentum Conservation Equation for the Fuel/Steel Chunks¶
Using an integration procedure similar to that used for the gas mixture, we obtain the following equation in finite difference form:
(16.4-195)
where
(16.4-196)
The optimal formulation of the convective terms can be obtained by using the input variable \(\text{IMOMEN} = 1\) and is similar to Eq. 16.4-174, where \({u''}_{\text{fu,i}}\) and \({u'}_{\text{fu,i}}\) are replaced by \(u_{l \text{u,i}}\) and \(u_{l \text{u,i}}\) and \(u_{l \text{u,i+1}}\), respectively. The quantity \(\theta_{l \text{u,i-1/2}}\) is defined by Eqs. 16.4-143 and 16.4-144, where \(\theta_{\text{Mi,i}}\) is replaced by \(\theta_{l \text{u,i}}\). The source terms are defined below:
(16.4-197)
No momentum sources due to chunk formation or remelting are present in Eq. 16.4-197, because the routines modeling these processes are called after the LEMOCO routine, and thus these effects will be considered later. The individual sources are presented below:
The term due to the gas mixture/chunk drag:
(16.4-198)
The generalized drag coefficient \({C'}_{\text{D,Mi,}l \text{u,i}}\) has been presented in Eq. 16.4-181.
The term due to the molten fuel/steel-chunk drag is as follows:
(16.4-199)
The generalized drag coefficient \({C'}_{\text{D,fu,} l \text{u,i}}\) has been presented in Eq. 16.4-181.
The momentum sink due to wall friction is:
where the generalized area of contact between chunks and clad/hexcan wall, \({A'}_{l \text{u,cl,i}}\) is defined as:
(16.4-200)
and is presented in Section 16.4.3.9. Equation 16.4-199 was obtained assuming that the frictional force between chunks and wall is due to the normal force generated by the pressure \(P_{\text{i}}\) and that the friction coefficient between the two solid surfaces is \(0.5 \cdot 10^{-3}\).
The momentum sink due to jumbling at the contraction at the boundary \(i\) is due to chunks arriving at an abrupt contraction, where they lose momentum upon hitting the wall normal to the flow path:
If \(u_{l \text{u,i}} < 0\) and \(A_{\text{i}} > A_{\text{i-1}}\),
(16.4-201a)
Otherwise,
(16.4-201b)
The sources \(\sum_{\text{n}}{\Gamma'}_{\text{Mo,} l \text{u,i-1}}^{n}\) are defined in a similar way, as shown below:
(16.4-202)
(16.4-203)
(16.4-204)
If \(u_{l \text{u,i}} \geq 0\) and \(A_{\text{i-1}} > A_{\text{i}}\),
(16.4-205a)
Otherwise,
(16.4-205b)
The source terms given by Eqs. 16.4-198 through 16.4-205 are substituted in Eq. 16.4-195 and after rearranging, we obtain the chunk momentum equation
(16.4-206)
16.4.3.8.4. The Simultaneous Solution of the Momentum Conservation Equations¶
The calculation of the new velocities in momentum cell i begins by calculating the coefficients AMX and DMX for the gas-mixture Eq. 16.4-170. The terms due to the mixture interaction with the molten fuel/steel and chunks are not included in AMX and DMX at this time. A check is then performed to verify if the momentum cell I contains only the gas mixture. If this is the case, the only equations solved is
(16.4-207)
and only the gas-mixture velocity is updated:
(16.4-208)
If either half of the momentum cell \(i\) contains molten fuel and/or steel, the coefficients are calculated for the momentum equations:
(16.4-209a)
(16.4-209b)
If the momentum cell does not contain fuel/steel chunks, these equations are solved simultaneously for \(\Delta u_{\text{Mi,i}}\) and \(\Delta u_{\text{fu,i}}\) and the new velocities are calculated:
(16.4-210a)
(16.4-210b)
It is noted that the coefficients AMX and DMX in Eqs. 16.4-209 are obtained by adding to the values calculated for Eq. 16.4-207 the additional terms due to the gas mixture-fuel interaction. If either half of the momentum cell contains fuel/steel chunks, the coefficients are calculated for the momentum equations in the form below:
(16.4-211a)
(16.4-211b)
(16.4-211c)
The coefficients that have been calculated using for Eqs. 16.4-210 are updated by adding the terms due to the presence of chunks. Equations 16.4-211 are solved simultaneously for \(\Delta u_{\text{Mi,i}}, \Delta_{\text{fu,i}}, \Delta u_{l \text{u,i}}\), by using a substitution method and the new velocities are calculated:
(16.4-212a)
(16.4-212b)
(16.4-212c)
16.4.3.9. Description of the Local Geometry¶
In order to fully define the energy and momentum source terms used in the conservation equations, we must supply the areas of contact between various components. These areas are obtained in LEVITATE by defining the local geometry in the routine LEGEOM. The definition of the geometry is based on the local flow regime and the configuration of the stationary elements, i.e., presence of fuel pins, presence of cladding, presence of frozen fuel crusts, etc.
16.4.3.9.1. Local Flow Regime Definition¶
Because the flow regimes are important in defining the local geometry, the decision about the local flow regime is made before the geometry definition in the LEVOFR routine. The physical models for the flow regimes are described in Section 16.4.1.4, and this section will describe only the decision process used to select the appropriate flow regime. The total flow regime is dependent on the local volumetric fraction of various components in the cell and on the previously established flow regime. The volumetric fraction for component \(i\), \(\alpha_{\text{i}}\), is defined as follows:
(16.4-213)
where \(A_{\text{ch,op}}\) is the local cross sectional area of the open flow channel. The flow regime in each cell is determined in the following manner:
If the previously established flow regime is bubbly fuel flow and
(a) if \(\frac{\theta_{\text{fu,i}} + \theta_{\text{se,i}}}{\theta_{\text{ch,op,i}} - \theta_{l \text{u,i}}} > \text{CIBBLY} \cdot 0.7\) and
if \(\theta_{\text{fu,i}} \geq \theta_{\text{se,i}} \cdot 0.9\) → bubbly fuel flow regime
if \(\theta_{\text{fu,i}} < \theta_{\text{se,i}} \cdot 0.9\) → bubbly steel flow regime
(b) if \(\frac{\theta_{\text{fu,i}} + \theta_{\text{se,i}}}{\theta_{\text{ch,op,i}} - \theta_{l \text{u,i}}} \leq \text{CIBBLY} \cdot 0.7\) and
if \(\theta_{\text{fu,i}} \geq \theta_{\text{se,i}}\) → annular fuel flow regime
if \(\theta_{\text{fu,i}} < \theta_{\text{se,i}}\) → annular steel flow regime
If the previously established flow regime is bubbly steel flow and
(a) if \(\frac{\theta_{\text{fu,i}} + \theta_{\text{se,i}}}{\theta_{\text{ch,op,i}} - \theta_{l \text{u,i}}} > \text{CIBBLY} \cdot 0.7\) and
if \(\theta_{\text{se,i}} > \theta_{\text{fu,i}} \cdot 0.9\) → bubbly steel flow regime
if \(\theta_{\text{se,i}} \leq \theta_{\text{fu,i}} \cdot 0.9\) → bubbly fuel flow regime
(b) if \(\frac{\theta_{\text{fu,i}} + \theta_{\text{se,i}}}{\theta_{\text{ch,op,i}} - \theta_{l \text{u,i}}} \leq \text{CIBBLY} \cdot 0.7\) and
if \(\theta_{\text{se,i}} \geq \theta_{\text{fu,i}}\) → annular steel flow regime
if \(\theta_{\text{se,i}} < \theta_{\text{fu,i}}\) → annular fuel flow regime
If the previously established flow regime is annular fuel or steel flow and
(a) if \(\frac{\theta_{\text{fu,i}} + \theta_{\text{se,i}}}{\theta_{\text{ch,op,i}} - \theta_{l \text{u,i}}} < \text{CIBBLY}\) and
if \(\theta_{\text{fu,i}} \geq \theta_{\text{se,i}}\) → annular fuel flow regime
if \(\theta_{\text{fu,i}} < \theta_{\text{se,i}}\) → annular steel flow regime
(b) if \(\frac{\theta_{\text{fu,i}} + \theta_{\text{se,i}}}{\theta_{\text{ch,op,i}} - \theta_{l \text{u,i}}} \geq \text{CIBBLY}\) and
if \(\theta_{\text{fu,i}} \geq \theta_{\text{se,i}}\) → bubbly fuel flow regime
if \(\theta_{\text{fu,i}} < \theta_{\text{se,i}}\) → bubbly steel fuel flow regime
The input constant CIBBLY defines the threshold for the transition from the annular to the bubbly flow regime. In the axial cells where the pins have not yet been disrupted the value of CIBBLY is given by the input constant CIBBIN. In disrupted nodes the value of CIBBLY is given the input constant CIBBDI. The recommended value for CIBBIN is 0.7, and for CIBBDI the recommended value is 0.2. Once a bubbly flow regime has been established, a hysteresis effect is assumed to exist and the transition threshold back to annular flow is CIBBLY \(\cdot\) 0.7. Similar hysteresis effects are used for the transitions from steel to fuel and vice versa within the bubbly flow regime. Finally, it is noted that the volume fractions used in the flow regime decision are based on the newly calculated densities and thus are consistent with the conditions at the end of the current time step.
16.4.3.9.2. Description of the Local Geometry of the Stationary and Moving Components¶
The definition of the local geometry of both stationary and moving components is performed by the LEGEOM routine. The physical boundaries of the rod bundle channel modeled in LEVITATE are the pin cladding and the hexcan wall. Because of the different behavior of these boundaries, the channel is visualized as being divided into two separate channels, one associated with the fuel pins and another associated with the hexcan wall, as shown in Figure 16.4.16. The flow area is partitioned between these two channels in proportion to the wetted perimeter of the boundaries:
(16.4-214)
(16.4-215)
where \(L_{\text{cl,i}}\) and \(L_{\text{sr,i}}\) represent the perimeter of the pins and hexcan wall in cell \(i\), respectively. It is emphasized that LEVITATE models the whole subassembly, and not one pin representing the subassembly. Thus, \(L_{\text{cl,i}}\) represents the perimeter of all the pins in the bundle. In the special situation when no pins are present at a certain axial location due to pin disruption, the perimeter \(L_{\text{cl,i}} = 0\), and the area of the channel associated with the cladding, \(A_{\text{ch,cl,i}}\) becomes zero. Each of the two channel is treated, for the purpose of defining the geometry, as a rectangular channel, with one dimension being the perimeter \(L\) and the other a characteristic length, \(l\). This characteristic length is defined as follows:
(16.4-216)
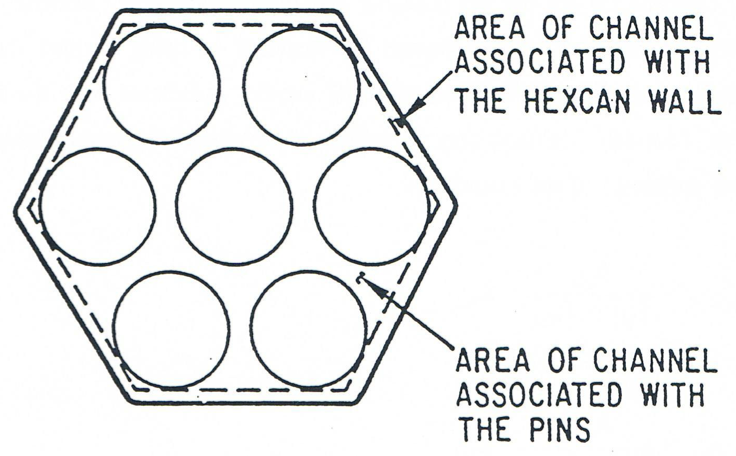
Figure 16.4.16 Partition of Subassembly Flow Area into Two Distinct Channels¶
The characteristics length \(l\) characterizes the width of the channel and serves as an indicator for the maximum thickness of the fuel crusts that can form on the pins and/or the hexcan wall. The conceptual representation of these channels is presented in Figure 16.4.17. The fuel crust, when present, is characterized by length \(L_{\text{ff,cl,i}}\) (and \(L_{\text{ff,sv,i}}\)) and thickness \(l_{\text{ff,cl,i}}\) (and \(l_{\text{ff,sv,i}}\)). However, instead of storing the crust \(L_{\text{ff}}\), two area coefficient are used:
(16.4-217)
and
(16.4-218)
As explained in Section 16.5, the fuel crust can occasionally contain molten or frozen steel, which is taken into account when the crust size is calculated. The crust growth is dependent on the initial conditions, the amount of new frozen fuel, and the local flow regime. This process will be presented later in this chapter.
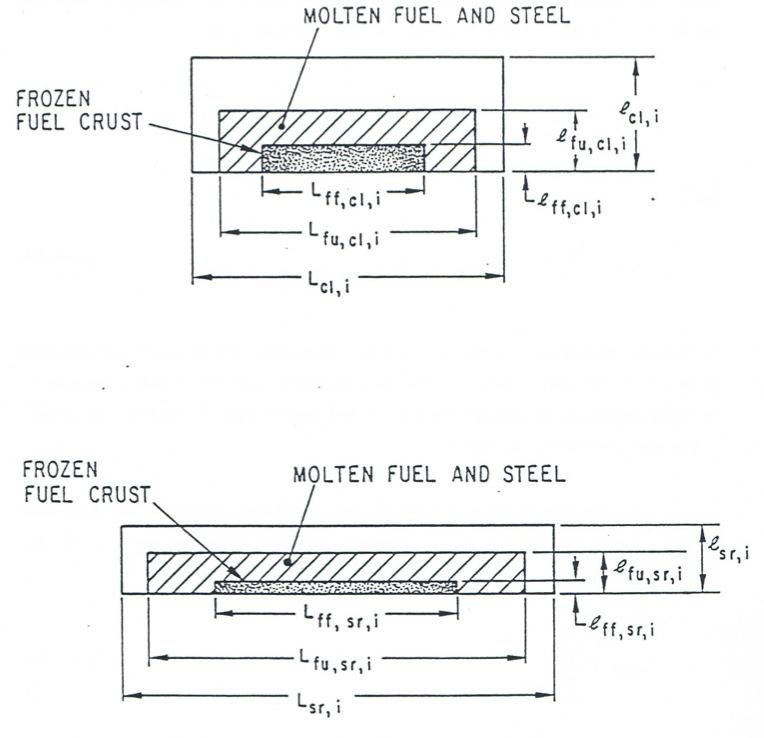
Figure 16.4.17 Conceptual Representation of the Pin and Hexcan Wall Channels¶
The configuration of the molten material, fuel and/or steel, is characterized by the length \(L_{\text{fu,cl,i}} \left( L_{\text{fu,sr,i}} \right)\) and thickness \(l_{\text{fu,cl,i}} \left( l_{\text{fu,sr,i}} \right)\). However, instead of storing the length \(L_{\text{fu}}\), two are coefficients are used:
(16.4-219)
(16.4-220)
Note that the coefficient \(C_{\text{fu,cl,i}}\) represents the fraction of clading area covered by molten fuel and fuel crust. The same applies to \(C_{\text{fu,sr,i}}\). All the contact areas required for the energy and momentum equations are defined by using the lateral area of the clad \(A_{\text{cl,i}}^{L}\) and hexcan wall \(A_{\text{sr,i}}^{L}\) and the appropriate area coefficients. Other area conditions used are:
\(C_{\text{fu,f} l \text{,cl,i}}\) - fraction of cladding crust area covered by molten fuel in cell \(i\)
\(C_{\text{fu,ff,sr,i}}\) - fraction of structure crust area covered by molten fuel in cell \(i\)
\(C_{\text{se,cl,i}}\) - fraction of cladding area covered by molten steel and fuel crust in cell \(i\)
\(C_{\text{se,sr,i}}\) - fraction of hexcan wall area covered by molten steel and fuel crust in cell \(i\)
\(C_{\text{se,ff,cl,i}}\) - fraction of cladding crust area covered by molten steel in cell \(i\)
\(C_{\text{se,ff,sr,i}}\) - fraction of hexcan wall crust area covered by molten steel in cell \(i\)
To each of these coefficients is attributed a specific value in the routine LEGEOM, depending on the flow regime and the initial conditions. Most of these values are self-explanatory and can be understood by looking a Figure 16.4.1, which illustrates the material configuration in each LEVITATE flow regime. Some additional comments are required for the partial annual fuel flow regime. To fully describe this flow regime, the following assumptions were made:
- The molten fuel film maintains a constant ratio \(\frac{l_{\text{fu,i}}}{L_{\text{fu,i}}}\) both for the clad and the hexcan wall. This ratio is defined by:
(16.4-221)
when no fuel crusts are present. It is built into the Eq. 16.4-223 and the user can affect it value only by changing the input constant CIANLR. This assumption leads to a gradual increase of the film-covered perimeter, together with a film thickness increase, whenever the amount of molten fuel increases.
- The partial annual flow becomes fully annular when the volume fraction of the molten fuel/steel reaches a certain input value, i.e., when
(16.4-222)
The existing fuel crust should be taken into account when calculating the coefficients \(C_{\text{fu,cl,i}}\) and \(C_{\text{fu,sr,i}}\).
These assumptions lead to the following definition for the area coefficient \(C_{\text{fu,cl,i}}\) in the annular fuel flow regime
(16.4-223a-b)
For nodes where the fuel pins are undisrupted, CIANLR is set equal to the input value CIANIN, currently 0.5. For disrupted nodes, CIANLR is equal CIANDI. A similar formula applies to \(C_{\text{fu,sr,i}}\).
Another aspect treated in LEGEOM, which will be discussed in this section, is the change in the fuel crust geometry due to additional fuel freezing. It is noted that other aspects such as steel freezing, crust breakup and remelting are treated in the routine LEFREZ and will be discussed in Section 16.5. Also, other aspects related to the chunk geometry are treated in the LETRAN routine and will be introduced in Section 16.4.3.10.
The amounts of fuel/steel which have to be added to the fuel crusts due to freezing are calculated in the LEFREZ routine in the previous time step. In the routine LEGEOM, these amounts are converted to corresponding are changes \(\Delta A_{\text{ff,cl,i}}\) and \(\Delta A_{\text{ff,se,i}}\). The decision on how to modify the crust parameters \(L_{\text{ff,cli,i}}\), \(l_{\text{ff,cl,i}}\), \(L_{\text{ff,sr,i}}\) and \(l_{\text{ff,sr,i}}\) is made in the following way (we will refer to the crust on the cladding only):
If no previous fuel crest is present and if the local fuel flow regime is partially annular flow, the original crust has the same thickness as the molten fuel film; however, if the local fuel flow regime is bubbly, the original crust is rather thin and the area coefficient \(C_{\text{ff,cl,i}}\) is obtained as follows:
(16.4-224)
where CIBBFZ is a constant, which is currently set equal to the input constant CIBBDI. If a previously formed crust is present the thickness of the crust is first increased until it reaches the thickness of he fuel film or the channel characteristic size \(l_{\text{cl,i}}\), whichever comes first. Then the length of the crust \(L_{\text{ff,cl,i}}\) is increased until \(C_{\text{ff,cl,i}} = 1\).
16.4.3.9.3. Description of the Fuel/Steel Chunk Geometry¶
The chunks modeled in LEVITATE have a cylindrical geometry, as shown in Figure 16.4.18. They are characterized by the radius \(R\), which is different in each axial cell. The length is related to the radius by the input constant ASRALU, which defines the ratio \(L/2R\) and has currently the recommended value 1. Each chunk can contain either fuel, or steel or both. The density of the steel chunks is constant and determined by the input variable RHSESO. The fuel chunks, however, have a variable density, which accounts for the possible porosity of the frozen fuel.
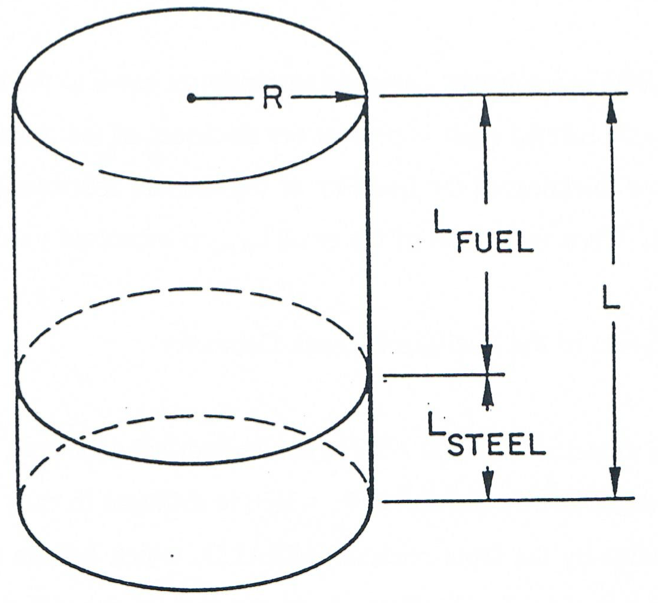
Figure 16.4.18 Fuel/Steel Chunk Geometry¶
The original geometry of the chunks depends on their origin. Several mechanisms have been identified which lead to the formation of solid fuel/steel chunks:
A. Disruption of the original fuel pins, which can occur when the cladding is locally molten, leading to the formation of relatively large fuel chunks. In this case the characteristic radius of the chunks is determined from:
(16.4-224-1)
where
\(\Delta R_{\text{pin,i}}\) - is the thickness of the solid fuel pin wall which separate the pin cavity from the coolant channel
\(\Delta L_{\text{perimeter,pin,i}}\) - is the characteristic size of the chunks which is obtained by dividing the pin perimeter by the number of radial cracks present at any axial location. The number of radial crack currently used is 8.
If the input variable RALUDI is zero, the code will use the above formula to determine the radius of the new chunks. However, this calculation can be overridden by setting RALUDI to a non-zero value. The radius of the newly formed chunks will be set equal to RALUDI.
B. Breakup of the frozen fuel crust that was formed previously on the cladding and hexcan wall. The characteristic radius of these chunks is determined from:
(16.4-224-2)
or
(16.4-224-3)
where
\(\Delta A_{\text{ffc,i}}\) - is the cross sectional area of the frozen fuel crust which breaks up during the current time step, in the axial cell \(i\)
\(\Delta A_{\text{ffs,I}}\) - is similar to \(\Delta A_{\text{ffc,i}}\), but applies to the fuel crust associated with the hexcan wall.
C. Local bulk freezing of the fuel when no solid support for crust formation is present. The characteristic radius of the chunks is obtained from:
(16.4-224-4)
where
\(\Delta A_{\text{fu,I}}\) - is the change in the cross sectional area of the molten fuel component due to removal of frozen fuel.
The volume of all the newly formed chunks in the axial cell \(i\) is calculated as follows:
(16.4-224-5)
where
\(\Delta {\rho'}_{\text{fl,i}}\) - is the generalized density of the fuel component in the newly formed chunks
\(\Delta {\rho'}_{\text{sl,i}}\) - is the generalized density of the fuel component in the newly formed chunks
The number of new chunks is obtained by dividing the total volume \(\Delta V_{l \text{u,i}}\) by the volume of a single chunk:
(16.4-224-6)
The new chunks will generally have different characteristics from the chunks already present in a cell. Because only one type of chunks can exist in one cell, the two categories are merged in one chunk population with properties reflecting the characteristics of both original components. This process is outlined below. Note that the same problem can arise in any cell even without the formation of new chunks due to the flux of chunk from neighboring cells. The first step in the merging of the two chunk categories is to define the radius of the resulting chunks.
(16.4-224-7)
The new chunk radius is a weighted average of the radii of the two chunk categories. The weights can be selected b the user, by changing the input integer \(\text{ILUMER}\), which can have the values 0, 1, 2, or 3. For \(\text{ILUMER} = 0\), the weights are equal to the number of chunks in the two populations. The recommended value is 3, for which the weights are proportional to the total volume. The number of resulting chunks is given by:
(16.4-224-8)
where the radius \(R_{l \text{,u,i}}^{n + 1}\) is defined by 16.4-224-7. Finally the fraction of steel in the chunks is given by:
(16.4-224-9)
The quantities \(L_{\text{FUEL}}\) and \(L_{\text{STEEL}}\) are introduced in Figure 16.4.18.
If the input variable RALUFZ is zero, then the code will use the above formulas to determine the radius of the new chunks formed by crust break-up and/or bulk freezing. However, if RALUFZ is not zero, the radius of the newly formed chunks will be set equal to RALUFZ.
16.4.3.10. Source Terms in the Energy and Momentum Equations¶
This section completes the description of the channel hydrodynamic model. It presents in detail the formulation of the source terms used in the energy equations, as introduced previously. It also presents some components of the source terms used in the momentum equations. The description of these source terms has been delayed until now for two reasons: first, the geometry elements introduced in Section 16.4.3.9 are needed for the definition of the source terms; second, all the elements described below are calculated in the routine LETRAN, and thus it was deemed preferable to describe them separately from the energy and momentum equations which are solved elsewhere.’
16.4.3.10.1. Source Terms in the Energy Equations¶
In the energy conservation equations, we introduced the source terms in the following form:
For the fuel energy Eq. 16.4-14:
(16.4-225)
For the steel energy eq. 16.4-26:
(16.4-226)
For the fuel chunk energy
(16.4-227)
For the steel chunk energy equation:
(16.4-228)
For the gas-mixture equation
(16.4-229)
where
(16.4-230)
We will now proceed to define all generalized heat-transfer coefficients that appear in Eqs. 16.4-225 through 16.4-230. As shown in Eq. 16.4-230 both \(H_{\text{j,k,i}}\) and \(A_{\text{j,k,i}}\) will have to be defined. Special reference will be made to each flow regime, and a short description of the physical model will be included.
16.4.3.10.1.1. Heat-transfer Coefficient between Fuel and Sodium \({H'}_{\text{fu,Na,i}}\)¶
For the annular and bubbly steel flow regimes, there is no contact between the fuel and sodium:
(16.4-231)
For the annular fuel flow regime, the heat-transfer coefficient is defined as follows:
(16.4-232)
where \(H_{\text{fu,i}}\) is a convection-type transfer coefficient on the fuel side:
(16.4-233)
and the sodium heat-transfer coefficient in the two-phase region is defined as:
(16.4-234)
where \(H_{\text{Na,i}}^{\text{Single,Phase}}\) is defined in Eq. 16.4-235.
The convective sodium heat-transfer coefficient in the single-phase region is defined below:
(16.4-235)
The area of contact between sodium and molten fuel is defined as follows:
(16.4-236)
For the bubbly fuel flow regime, the heat-transfer between sodium and fuel is described as taking place between a continuous fuel component and spherical sodium bubbles. The number of sodium bubbles (and thus their radius) varies from one bubble at the transition boundary between annular and bubbly flow to a maximum number determined by a maximum number determined by a minimum radius of the bubble:
(16.4-237)
(16.4-238)
The actual radius of the bubbles is obtained by assuming an exponential variation between \(R_{\text{max}}\) and \(R_{\text{min}}\), dependent on how far from the flow regime transition we are in the cell \(i\):
(16.4-239)
where \(\theta_{\text{Mi,bubbly}}\) is the mixture volume fraction required for the transition from the annular to bubbly flow.
The number of bubbles is defined by:
(16.4-240)
and the heat-transfer area becomes:
(16.4-241)
The heat-transfer coefficient is determined by the heat-transfer resistance on the fuel side and the resistance of the bubble:
(16.4-242)
where \(H_{\text{fu,i}} = 3 \cdot 10^{4}\) J/m2 K-s and wad determined by analyzing the transient solution describing the propagation of a step change in temperature in a semi-infinite medium. For a typical LEVITATE time step \(\Delta t\) and a temperature change \(\Delta T, H_{\text{fu,i}}\) was determined from:
(16.4-243)
Where \(Q \left( x = 0 \right)\) is the heat flux at the boundary of the semi-infinite medium, in J/m2 · s.
The heat-transfer coefficient in the bubble, \(H_{\text{Na,i}}\) is defined by Eq. 16.4-234 for the two-phase sodium region. For single-phase sodium:
(16.4-244)
16.4.3.10.1.2. Heat-transfer Coefficient between Fuel and Cladding or Structure \({H'}_{\text{fu,cl,i}}\) and \({H'}_{\text{fu,sr,i}}\)¶
For the annular and bubbly steel flow regimes the fuel is in contact with neither the cladding nor the structure.
(16.4-245)
For the annular fuel flow regime, the heat-transfer coefficient from fuel to cladding and structure is defined as:
(16.4-246)
and the respective heat-transfer areas are:
(16.4-247)
For the bubbly fuel flow regime, the heat-transfer coefficients are defined as follows:
(16.4-248)
and the respective heat-transfer areas are:
(16.4-249)
16.4.3.10.1.3. Heat Transfer between Fuel and Frozen Fuel Crusts on Cladding and Structure \({H'}_{\text{fu,ffc,i}}\) and \({H'}_{\text{fu,ffs,i}}\)¶
These coefficients are zero in the annular and bubbly steel flow regimes.
(16.4-250)
For the annual fuel flow regime, the heat-transfer coefficients are defined as:
(16.4-251)
(16.4-252)
where \(H_{\text{fu,i}}\) is given by Eq. 16.4-246 and \(l_{\text{ff,cl,i}}\) and \(l_{\text{ff,sr,i}}\) have been defined in Section 16.4.3.9, which describes the local geometry. The respective heat-transfer areas are:
(16.4-253)
and
(16.4-254)
For the bubbly fuel flow regime, the heat-transfer coefficients are given by Eqs. 16.4-251 and 16.4-252, but \(H_{\text{fu,i}}\) in these is given by Eq. 16.4-248 rather than Eq. 16.4-246. The heat-transfer areas are given by:
(16.4-255)
(16.4-256)
16.4.3.10.1.4. Heat-transfer Coefficient between Fuel and Steel \({H'}_{\text{se,fu,i}}\)¶
In the annular and bubbly steel flow regimes, the fuel exists in the form of droplets imbedded in the continuous molten steel. The radius of the fuel droplets varies between \(R_{\text{fu,droplet,min,i}} = 1 \cdot 10^{-4}\) m and \(R_{\text{fu,droplet,max,i}} = l_{\text{fu,cl,i}}\). The actual radius is calculated as follows:
If \(1 \geq \frac{\theta_{\text{fu,i}}}{\theta_{\text{se,i}}} \geq 0.5\)
(16.4-257a)
If \(\frac{\theta_{\text{fu,i}}}{\theta_{\text{se,i}}} < 0.5\), then
(16.4-257b)
The number of fuel droplets and heat-transfer area are calculated from:
(16.4-258)
and
(16.4-259)
The heat-transfer coefficient is obtained as follows:
(16.4-260)
where \(H_{\text{se,i}} = 4 \cdot 10^{4}\) and is obtained in a manner similar to Eq. 16.4-243.
For the annual and bubbly fuel flow regimes, the situation is reversed, and the steel exists in the form of droplets imbedded in the continuous molten fuel. The radius of the steel droplet is defined as follows:
For \(\frac{\theta_{\text{se,i}}}{\theta_{\text{fu,i}}} > 0.5\)
(16.4-261a)
For \(\frac{\theta_{\text{se,i}}}{\theta_{\text{fu,i}}} \leq 0.5\)
(16.4-261b)
Note that the definitions 16.4-257 and 16.4-261 lead to a continuous change in \(R_{\text{droplet,i}}\) across the transition from a fuel to a steel flow regime. The number of steel droplets and the heat-transfer area are obtained from formulas similar to 16.4-258 and 16.4-259. The heat-transfer coefficient is defined by:
(16.4-262)
where \(H_{\text{fu,i}} = 3 \cdot 10^{4}\) and has already been explained in Eq. 16.4-243.
16.4.3.10.1.5. Heat-transfer Coefficients between Fuel and Fuel and Steel Chunks \({H'}_{\text{fu,fl,i}}\) and \({H'}_{\text{fu,sl,i}}\)¶
As explained in 16.4.3.9.2, the fuel and steel chunks have a cylindrical geometry and the aspect ratio R/L can be varied via the input. Thus, it is necessary to distinguish between the heat transfer across the surface normal to the flow \(A_{\text{f} l \text{,i}}^{N}\) and that across the surface parallel to the flow direction, \(A_{\text{f} l \text{,i}}^{L}\). Note that the chunks are always assumed to be parallel to the flow direction, and that the total surface of the fuel chunks is given by \(A_{\text{f} l \text{,i}}^{L} + A_{\text{f} l \text{,i}}^{N}\). Thus, the generalized heat-transfer coefficient between the fuel and the fuel and steel chunks can be written as:
(16.4-263)
(16.4-264)
For the steel flow regimes, both bubbly and annular, no contact is present between the molten fuel and chunks:
(16.4-265)
For the bubbly fuel flow regime, the heat-transfer coefficients are defined as follows:
(16.4-266)
and
(16.4-267)
where \(H_{\text{fu,i}}\) has been defined in Eq. 16.4-243. The corresponding heat-transfer areas are:
(16.4-268)
(16.4-269)
For the annular fuel flow regime, the chunks can have velocities quite different from those of the molten fuel, and convective effects must be taken into account. The heat-transfer coefficients are still defined by Eqs. 16.4-266 and 16.4-267, but \(H_{\text{fu,i}}\) is replaced by \(H_{\text{fu,i}} + H_{\text{fu,convective,i}}\), where \(H_{\text{fu,convective,i}}\) is defined as:
(16.4-270)
where
(16.4-270-1)
The heat-transfer areas for the annular flow are significantly different from those used for the bubbly fuel flow. The normal surface is not in contact with the molten fuel, thus:
(16.4-271)
The lateral heat transfer areas are defined as follows:
(16.4-272)
where \(F_{\text{area,bd,} l \text{u,i}}\) is the fraction of the area of the chunks in contact with the channel boundaries. It is obtained by assuming that chunks are uniformly distributed across the channel area and defining the contact area for the chunks near the boundary (currently the contact area is equal to \(0.5 \cdot A_{\text{fl,i}}^{L}\)). \(A_{\text{fu,s} l \text{,i}}^{L}\) is defined similarly to Eq. 16.4-272, but \(A_{\text{f} l \text{,i}}^{L}\) is replaced by \(A_{\text{s} l \text{,i}}^{L}\).
16.4.3.10.1.6. Heat-transfer Coefficients between the Molten Steel and Fuel and Steel Chunks \({H'}_{\text{se,fl,i}}\) and \({H'}_{\text{se,sl,i}}\)¶
For the annular and bubbly fuel flow regimes, these coefficients are zero because the steel and the chunks are not in contact.
For the annular and bubbly steel flow regimes, the considerations made in Section 16.4.3.10.1.5 still apply and the Eqs. 16.4-263 through 16.4-272 can be used, but \(H_{\text{fu,i}}\) is replaced by \(H_{\text{se,i}}\), defined similarly for steel, and \(H_{\text{fu,convective,i}}\) is replaced by \(H_{\text{se,convective,i}}\) defined below:
(16.4-273)
16.4.3.10.1.7. Heat-transfer Coefficients between Molten Steel and Cladding and Structure \({H'}_{\text{se,cl,i}}\) and \({H'}_{\text{se,sr,i}}\)¶
The coefficients are zero for the fuel flow regimes, both annular and bubbly:
(16.4-274)
For the annular steel flow regime, heat-transfer coefficients are defined as follows:
(16.4-275)
and the respective areas, \(A_{\text{se,c} l \text{,i}}\) and \(A_{\text{se,sr,i}}\) are identical to Eqs. 16.4-247.
For the bubbly steel regime, the heat-transfer is given by:
(16.4-276)
and the heat-transfer areas \(A_{\text{se,cl,i}}^{L}\) and \(A_{\text{se,sr,i}}^{L}\) are defined by Eq. 16.4-249.
16.4.3.10.1.8. Heat-transfer Coefficients between Steel and the Frozen Fuel on Cladding Structure \({H'}_{\text{se,ffc,i}}\) and \({H'}_{\text{se,ffs,i}}\)¶
These coefficients are zero for the fuel annular and bubbly flow regimes:
(16.4-277)
For the steel regimes, the considerations made in Section 16.4.3.10.1.3 for the fuel regimes apply. Thus, Eqs. 16.4-250 through 16.4-256 can be used to define the corresponding heat-transfer coefficients and transfer areas if one replaces \(H_{\text{fu,i}}\) by \(H_{\text{se,i}}\), defined as follows:
(16.4-278)
16.4.3.10.1.9. Heat Transfer between Steel and Sodium/Fission Gas \({H'}_{\text{se,Na,i}}\)¶
The coefficient is zero for the fuel flow regimes:
(16.4-279)
All considerations made for the fuel flow regimes in Section 16.4.3.10.1.1 apply here and Eqs. 16.4-232 through 16.4-244 should be used, if \(h_{\text{fu,i}}\) is replaced by \(H_{\text{se,i}}\), as appropriate. Thus, the heat-transfer coefficient for the annual steel regime becomes from Eq. 16.4-232:
(16.4-280)
where \(H_{\text{se,i}}\) is defined by Eq. 16.4-278. The same formula applies for the bubbly steel regime from Eq. 16.4-242, but \(H_{\text{se,i}}\) is defined in a manner similar to Eq. 16.4-243.
16.4.3.10.1.10. Heat-transfer Coefficients between Fuel Steel Chunks and Cladding and Structure \({H'}_{\text{cl,f} l \text{,i}}, {H'}_{\text{cl,s} l \text{,i}}, {H'}_{\text{sr,f} l \text{,i}}, {H'}_{\text{sr,s} l \text{,i}}\)¶
The chunks can be in contact with the cladding and structure only in the partial annular fuel flow regime (this is also the default when neither fuel not steel is present in the channel). For all other regimes, the above coefficients are equal to zero.
For the partial annular fuel flow regime, the heat-transfer coefficients are defined below:
(16.4-281)
(16.4-282)
The definition of the heat-transfer areas accounts for the fact that only the chunks close to the boundaries not covered by molten fuel exchange energy directly with the cladding and structure.
(16.4-283)
(16.4-284)
(16.4-285)
(16.4-286)
16.4.3.10.1.11. Heat-transfer between Sodium/Fission Gas Mixture and the Fuel/Steel Chunks \({H'}_{\text{Na,f} l \text{,i}}\) and \({H'}_{\text{Na,s} l \text{,i}}\)¶
These coefficients are zero in the bubbly flow regimes when there is no contact between sodium and chunks.
(16.4-287)
For the annular fuel and steel regimes the generalized coefficients are defined as follows:
(16.4-288)
(16.4-289)
The heat-transfer coefficients in Eqs. 16.4-288 and 16.4-290 are defined below:
(16.4-290)
(16.4-291)
The respective heat-transfer areas are defined as follow:
(16.4-292)
(16.4-293)
16.4.3.10.1.12. Heat-transfer between the Fuel and Steel Solid Chunks \(H_{fl,sl,i}^{'}\)¶
This coefficient is different from zero only when both fuel and steel chunks are present in a cell. Given the geometry of the chunks presented in Section 16.4.3.9, the heat-transfer coefficient is defined by:
(16.4-294)
and the heat-transfer area by:
(16.4-295)
16.4.3.10.1.13. Heat Transfer between Fuel/Steel Chunks and the Frozen Fuel on Cladding and Structure, \({H'}_{\text{f} l \text{,ffc,i}}, {H'}_{\text{f} l \text{,ffs,i}}, {H'}_{\text{s} l \text{,ffc,i}}, {H'}_{\text{s} l \text{,ffs,i}}\)¶
These coefficients are non-zero only if there is little molten fuel and/or steel present, i.e.:
(16.4-296)
and the frozen fuel crust covers a significant fraction of the channel perimeter, i.e.:
(16.4-297)
If the above conditions are satisfied, the heat-transfer coefficients are defined as follows:
(16.4-298)
(16.4-299)
The respective heat-transfer areas are defined below:
(16.4-300)
(16.4-301)
The areas for the steel chunks, \(A_{\text{s} l \text{,ffc,i}}\) and \(A_{\text{s} l \text{,ffs,i}}\) can be obtained from the above definitions by replacing \(A_{\text{f} l \text{,i}}^{L}\) with \(A_{\text{s} l \text{,i}}^{L}.\)
16.4.3.10.1.14. Heat-transfer Coefficients between Sodium/Fission Gas and Cladding or Structure \({H'}_{\text{Na,cl,i}}\) and \({H'}_{\text{Na,sr,i}}\)¶
These coefficients are non-zero only for the partial annular fuel flow regime. In all other regimes, the sodium/fission gas mixture is not in direct contact with the cladding and structure. The heat-transfer coefficient is calculated as follows:
If \(\alpha_{\text{Na,i}} \leq 0.15\),
(16.4-302)
The value of \(k_{\text{N1}}\) is given by the input constant \(\text{CDNL}\). The constants \(C1\), \(C2\) and \(C3\) are the source input constants used in the preboiling model.
If \(\alpha_{\text{Na,i}} > 0.15\) and
\(T_{\text{Na,i}} \leq T_{\text{cl,i}}\) (boiling situation)
(16.4-303a-c)
The value of \(k_{\text{Mi}}\) is given by the input constant CDVG.
\(T_{\text{Na,i}} > T_{\text{cl,i}}\) (condensation situation)
(16.4-304a-d)
It is noted that the branch Eq. 16.4-304b has not been implemented in the initial release version but exists in the chunk version.
For \(\alpha_{\text{Na,i}} > .15\), the heat-transfer coefficient between sodium and structure is obtained from Eq. 16.4-303 for \(T_{\text{Na,i}} \leq T_{\text{sr,i}}\) and from Eq. 16.4-304 for \(T_{\text{Na,i}} > T_{\text{sr,i}}\).
The respective heat-transfer areas are defined as follows:
(16.4-305)
and
(16.4-306)
16.4.3.10.1.15. Heat-transfer coefficients between sodium and Frozen Fuel on Cladding and Structure \({H'}_{\text{ffc,Na,i}}\) and \({H'}_{\text{ffs,Na,i}}\)¶
These coefficients are non-zero only in the partial annular flow regime. For this regime, the heat transfer coefficients are defined below:
(16.4-307)
(16.4-308)
where \(H_{\text{Na,i}}\) is defined by Eq. 16.4-234.
The respective heat-transfer areas are defined as follows:
(16.4-309)
(16.4-310)
16.4.3.10.2. Friction Coefficients Used in the Momentum Equations¶
In Section 16.4.3.8, which describes the momentum equations, several friction coefficients used in the momentum source terms were left undefined. These coefficients are calculated in the routine LETRAN and are presented in this section.
16.4.3.10.2.1. Friction Factor Between Mixture and Cladding/Structure \(f_{\text{Mi,i}}\)¶
This factor was referenced in Eq. 16.4-150. It is zero for all flow regimes except the partial annual fuel flow regime. For this flow regime, it is defined as follows:
(16.4-311)
where AFRV, BFRV are input constants and \(C_{\text{Mi,bd,i}}\) is the fraction of the channel boundary (cladding + structure + crust) which is in direct contact with the gas mixture in cell \(i\). It is defined as:
(16.4-312)
where
(16.4-313)
and
(16.4-314)
16.4.3.10.2.2. Friction Factors Between Mixture and Fuel \(f_{\text{Mi,fu,i}}\) and \(f_{\text{Mi,se,i}}\)¶
These factors were referenced in Eq. 16.4-152. The factor \(f_{\text{Mi,fu,i}}\) is used only in the partial annular fuel flow regime and is defined below:
(16.4-315)
\(\text{Re}_{\text{Mi,fu,i}}\) is defined as:
(16.4-316)
and \(C_{\text{Mi,fu,i}}\), the fraction of the mixture perimeter in contact with the molten fuel is given by:
(16.4-317)
The factor \(f_{\text{Mi,se,i}}\) is used in the annular steel flow regime and takes into account the possibility of flooding. It is defined as follows:
(16.4-318)
Where the flooding coefficient depends on the velocity ratio \(V_{\text{RATIO}}\):
(16.4-319)
(16.4-320)
(16.4-321)
The value of \(C_{\text{FLOOD,i}}\) is also dependent on the previous flooding history as shown below:
If \(C_{\text{FLODD,i}}^{n} \leq 1:\)
(16.4-322)
If \(C_{\text{FLODD,i}}^{n} > 1\)
(16.4-323)
16.4.3.10.2.3. Several Area Coefficients Used in the Momentum Source Terms¶
The area coefficient \(C_{\text{AREA,Mi,fu,i}}\) has been introduced in Eq. 16.4-155. It defines the fraction of the lateral area of chunks in contract with the mixture and is zero for the fuel and steel bubbly flow regimes. For the annular flow regimes, it is calculated as follows:
(16.4-324)
The area coefficients \(C_{\text{AREA,se,i}}\) and \(C_{\text{AREA,fu,i}}\) have been introduced in Eqs. 16.4-177 and 16.4-178. They account for the fact that only a fraction of the fuel steel perimeter is in contact with the stationary walls. They are defined below:
For the fuel bubbly flow regime:
(16.4-325)
For the steel bubbly flow regime:
(16.4-326)
For the annular steel flow regime:
(16.4-327)
For the partial annular fuel flow regime:
(16.4-328)
16.4.3.11. Time Step Determination for the Channel Hydrodynamic Model¶
This section describes the calculation of the maximum time step for the coolant channel hydrodynamic model. This time step will be used in the determination of the LEVITATE time step as outlined in Section 16.7.3. The maximum channel time step is calculated using the sonic Courant condition for the multicomponent channel flow. Only a fraction of the Courant calculated time is used, to account for inaccuracies in the sonic velocity calculation. Thus:
(16.4-329)
The minimum in Eq. 16.4-329 is evaluated over all axial cells of the interaction region. The sonic velocity in each cell is calculated using an expression [16-14] for an adiabatic homogeneous two-phase mixture of liquid sodium and fission gas/sodium vapor. The compressibility of liquid fuel is much smaller than that of liquid sodium and thus the fuel is assumed to be incompressible in the calculation of the sonic velocity in the channel. The effect of fuel and steel vapor is not included.
(16.4-330)
where:
(16.4-331)
\(\gamma_{\text{vg}}\) = ratio of specific heat at constant pressure to that at constant volume for the fission gas/sodium vapor mixture. A value of 1.4 is used in the LEVITATE code
\(\text{CMNL}\) = compressibility of liquid sodium, an input constant
The fission-gas pressure \(P_{\text{fi}}\) and the sodium pressure \(P_{\text{Na}}\) are obtained as explained in Section 16.4.3.5.