14.4. Channel Hydrodynamics Model¶
14.4.1. Overview and Definition of Generalized Smear Densities¶
The treatment of the material motion in the coolant channels is more complex than that inside the pins because several material components (fuel, sodium, fission gas) and three different phases (solid, liquid, and gas) are involved. Of particular importance are the mass, energy and momentum interactions between the components and phases of this multi‑component, multi‑phase flow. These are largely determined by the local fuel configurations, which are in turn determined by the fuel flow regimes. Figure 14.4.1 depicts the possible fuel and liquid sodium configurations in an equivalent cylindrical channel. The outer perimeter of this equivalent cylindrical channel represents outer cladding surfaces and inner subassembly wall surfaces. The fuel flow regimes are extensively discussed in Section 14.4.3.1. Figure 14.4.2 gives an overview of the interactions between the various channel components that are described in detail in Section 14.4.3.4.
A one‑dimensional two‑fluid approach with variable flow cross section is used to calculate the momentum changes in the coolant channels. This means that two momentum conservation equations are solved. One of them calculates the velocity changes of the mixture of liquid sodium, sodium vapor, fission gas, and fuel vapor; the other calculates the velocity changes of the moving liquid or solid fuel. This approach is taken because the fuel‑to‑liquid sodium density ratio is more than 10, and a relatively rapid separation of these two components is likely. This is quite important for treating fuel coolant interactions (FCI’s) because it may be one of the major limiting processes.
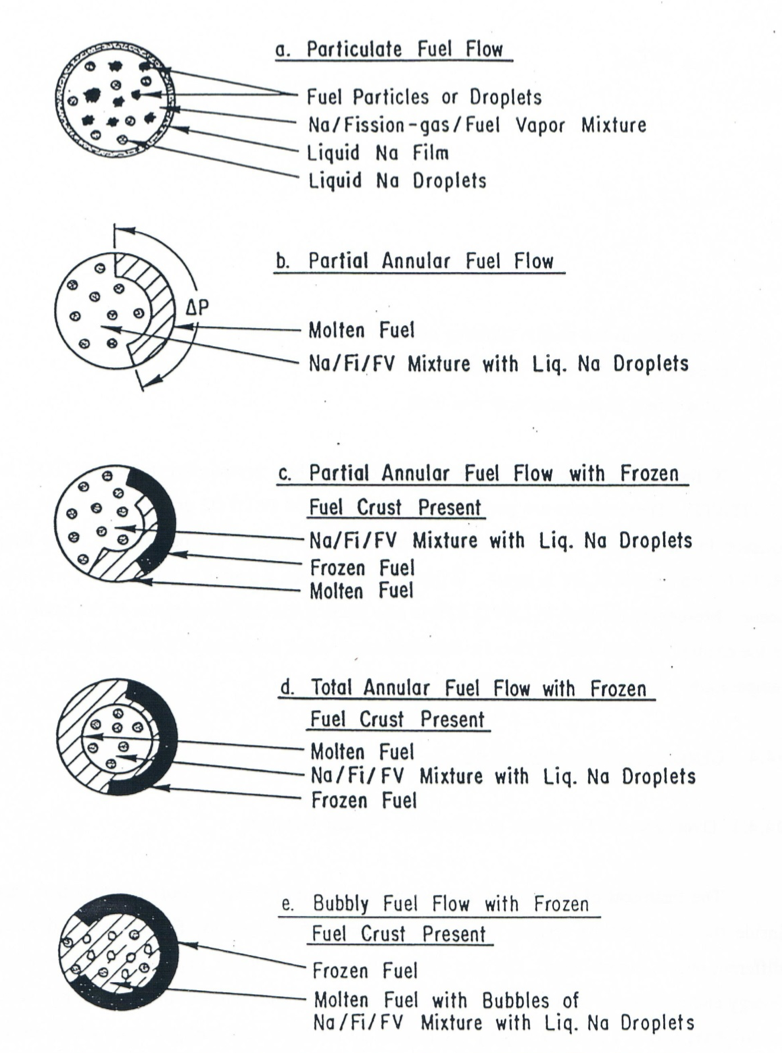
Figure 14.4.1 Illustration of the Possible Sodium and Fuel Flow Regimes as Well as the Fuel Freezing Patters in the PLUTO2 Model of the Coolant Channel¶
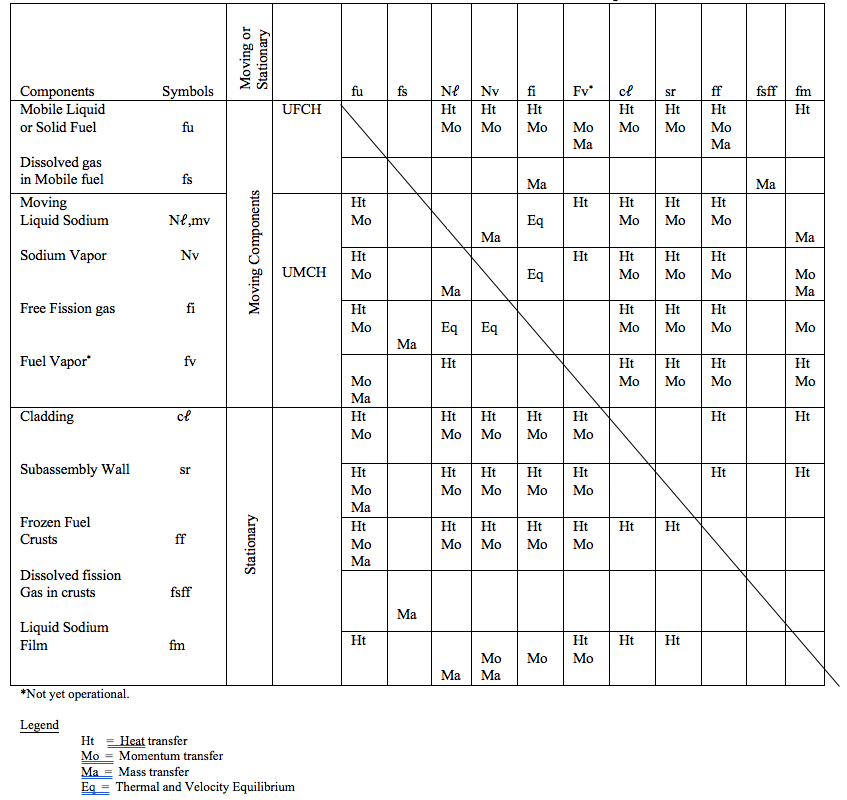
Figure 14.4.2 Table 14.4‑1. Overview of the Interaction Between the Channel Components in PLUTO2¶
There are four mass conservation equations for tracking moving components in PLUTO2; (a) for liquid or solid fuel and for fuel vapor 1, (b) for liquid sodium and sodium vapor, (c) for free fission gas, and (d) for fission gas still dissolved in the fuel. There are also mass conservation equations for the stationary fuel crust (i.e., plated‑out solid fuel) and for the stagnant sodium film.
A single energy conservation equation is solved for the mixture of liquid sodium (including the stagnant sodium film), sodium vapor, and free fission gas, which are all assumed to be in thermodynamic equilibrium. An energy conservation equation is solved for the moving solid fuel or for the two‑phase mixture of liquid fuel and fuel vapor. The latter two are assumed to be in thermodynamic equilibrium in the region where the fuel vapor pressure is larger than 10-2MPa. Outside this region, no fuel vapor is considered. There is also an energy equation for the solid fuel crusts.
The equation‑of‑state calculates the pressure for cells containing (a) liquid‑phase sodium, (b) two‑phase sodium, two‑phase fuel and fission gas, and (c) superheated vapor and fission gas.
Although Eulerian hydrodynamics is generally employed in the formulation of the equations, a Lagrangian treatment is used to track the moving upper and lower boundaries of the multiphase region. All finite difference equations are written in conservative form. A staggered mesh grid, with the velocities at the cell edges, and pressures, densities, and temperatures at the cell centers, is used. The spatial derivatives are evaluated by full donor cell differencing, which is also known as second upwind differencing. This approach is more stable for very non‑continuous conditions that are quite common in PLUTO2 applications although this is not as accurate as higher order schemes [14‑30, 14‑31].
The time differencing is mainly explicit, but there are also important implicit features involved. First, advantage is taken of the solution sequence of the conservation equations. The results of the mass conservation equations which are solved first, are used in the energy conservation equations. The results of these two sets of conservation equations and the results from the calculation of the fuel and gas ejection from the pins are used in the equation‑of‑state and provide an estimate of the channel pressure at the end of the time step. This is then used in the solution of the momentum conservation equations.
Another implicit feature that is of key importance for a stable velocity calculation of the lighter component is the simultaneous solution of the two momentum equations. The lighter component can experience strong and opposing pressure gradient and drag forces, which lead to oscillatory behavior for low density mixtures if a simultaneous solution is not performed [14‑32]. Also important is the implicit treatment of the potentially large heat transfer between the various hot and cold components.
The explicit aspect of the solution method is that the conservation equations at different axial locations are not solved in a coupled fashion. This means, for example, that a new velocity calculated at one mesh cell boundary does not have an immediate effect on the new velocity at the neighboring boundary. By not solving the equation sets simultaneously, one can avoid three potential problems. First, an iterative solution for the inversion of a complicated matrix, which can have convergence problems or may require many iterations, can be avoided. (A direct solution through Gaussian elimination does not seem to be easily feasible for more than two coupled equation sets.) Second, the later addition of certain terms to the equation set is relatively straightforward for explicit schemes but can be complicated for implicit schemes. Terms may have to be added to the equation set in order to make a code such as PLUTO2 work for heretofore unforeseen conditions or because the importance of additional terms may have to be investigated. Third, the matrix elements of an implicit solution technique for multi‑phase, multicomponent flows are usually complex and have no direct physical meaning. Therefore, they can complicate the debugging of such implicit solution schemes. However, a very stable implicit scheme that would decrease the code running time and diminish the truncation error introduced by the many time steps in an explicit scheme is desirable. This may not be a practical goal for the solution of the entire equation set in PLUTO2 but it would be a reasonable goal for selected equations such as the mass and momentum conservations of the light components.
Definition of the Generalized Smear Densities. A special feature of the PLUTO2 module (and of the LEVITATE module) is the use of generalized smear densities. This has been prompted by the presence of the many different components and the simplification of the differential and finite difference equations. The volume fractions are lumped together with the physical densities of the materials and therefore do not appear in the equations. Details about the smear densities in the fuel pin have already been described in Section 14.2.5. The pie chart in Figure 14.4.3 gives an example of the relative cross sectional areas involved at a certain axial location.
As discussed in Section 14.2.1, the same total cross sectional area of the pie, which is an input value AXMX, is used at all axial locations of the subassembly or the experimental loop considered. The relative sizes of the pie pieces can vary at different axial locations; pieces such as the pin piece can actually disappear at elevations above or below the pin bundles. There is no empty piece in the pie if one assumes the total area of the pie, AXMX, to be the total cross sectional area of a subassembly or an experimental loop. However, at elevations where the cross sectional area of the subassembly or the experimental loop is smaller than AXMX, an empty pie piece is necessary.
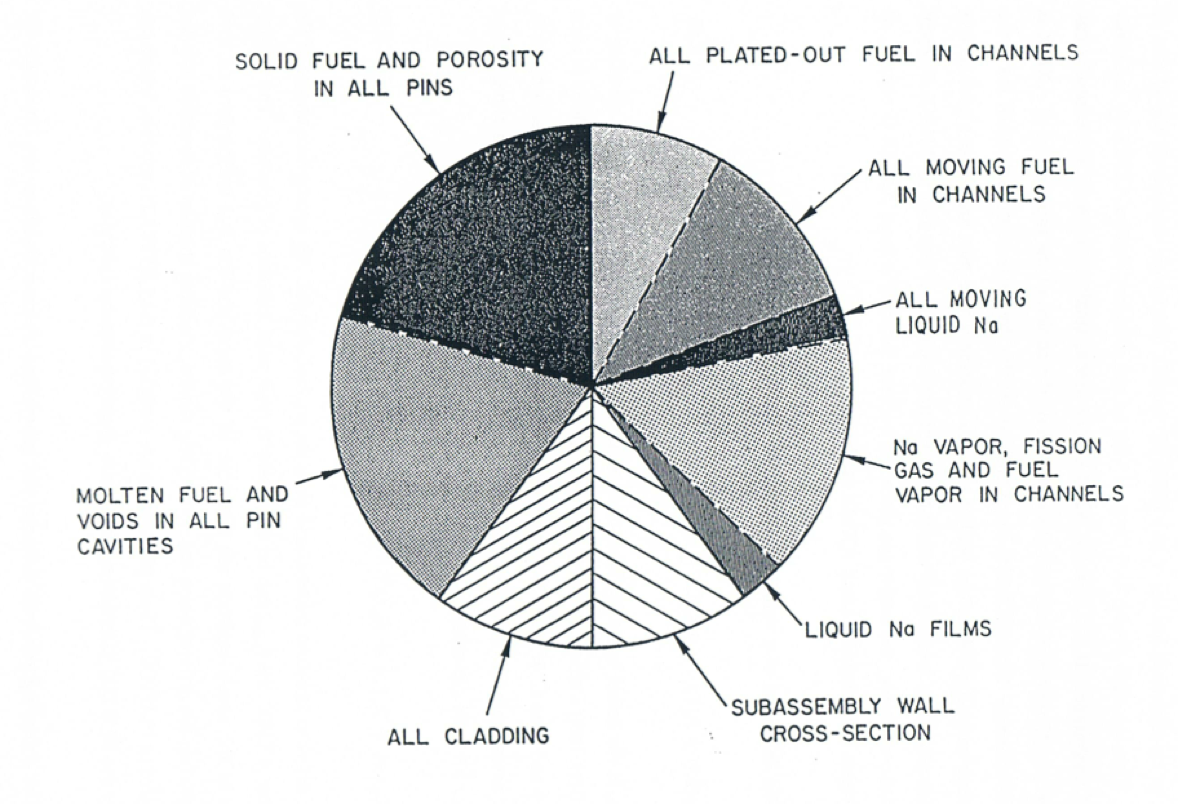
Figure 14.4.3 The Right-hand Side of This Pie Chart Illustrate the Possible Material Cross Sectional areas in the Coolant Channel, the Whole Pie Representing an Area AXMX, which is an Input Parameter¶
The calculational results of the PLUTO2 module should not depend on the choice of AXMX. This has been shown to be true as long as one does not change AXMX by too many orders of magnitude. If one changes AXMX very much, small differences in the results can occur due to differences in truncation errors. Thus, the choice of the input value of AXMX is one of convenience. The best choice for AXMX is usually the cross sectional area of the entire subassembly including the hexcan wall at an axial location where pins are present because this will lead to physically meaningful values of the volume fraction. If one uses an AXMX different from the above choice, the empty pie piece can become larger if a large AXMX is chosen, or even negative if a relatively small AXMX is chosen.
The definition of a volume fraction of a certain component \(k\) is:
(14.4‑1)
where \(A_{\text{k}}\) is the actual cross sectional area occupied by component \(k\) (e.g., all the cladding or all the frozen fuel) inside a fuel assembly or inside the can wall of an experimental loop at axial location \(z\) and time \(t\). If AXMX was chosen to be the entire subassembly cross section, the \(\theta_{\text{k}}\) gives the actual volume fraction of component \(k\) in a slice of a subassembly or an experimental loop. For all axial elevations,
(14.4‑2)
where sr refers to structure material and ch to the coolant channel. By appropriate choice of the input value AXMX, the \(\theta_{\text{empty}}\) can be made zero at most axial locations of concern. The volume fractions in the above equation are functions of the axial position but independent of time because no fuel-pin disintegration and no cladding motion, cladding ablation or structure ablation are modeled in PLUTO2. These phenomena are modeled in the LEVITATE module, which can take over the PLUTO2 calculation when these phenomena come into play.
The following relations between the generalized volume fractions are important for writing the channel hydrodynamics equations in PLUTO2:
(14.4‑3)
where
\(\theta_{\text{ch}}\) is the generalized coolant channel volume fraction which is always equal to the values at pin failure in PLUTO2;
\(\theta_{\text{ch, op}}\) is the generalized volume fraction of the open channel (i.e., the part of the channel available for the mobile components);
\(\theta_{\text{ff}}\) is the generalized volume fraction of the frozen fuel crusts;
(14.4‑4)
where
\(\theta_{\text{fu}}\) is the generalized volume fraction of the mobile liquid or solid fuel in the channel;
\(\theta_{\text{N1}}\) is the generalized volume fraction of the liquid sodium;
\(\theta_{\text{vg}}\) is the generalized volume fraction of the vapor/gas (i.e., void) space in the channel;
(14.4‑5)
where
\(\theta_{\text{N1, mv}}\) is the generalized volume fraction of the moving liquid sodium;
\(\theta_{\text{fm}}\) is the generalized volume fraction of the liquid sodium film.
The following generalized smear densities are defined:
(14.4‑6)
where
\(\rho_{\text{fuch}}\) is the generalized smear density of all the mobile fuel (solid, liquid and vapor) in the channel;
\(\rho_{\text{fu}}\) is the theoretical density of the liquid or solid fuel;
\(\rho_{\text{fv}}\) is the physical fuel vapor density;
(14.4‑7)
where
\({\rho'}_{\text{ff}}\) is the generalized smear density of the frozen fuel crust.
(14.4‑8)
where
\(\rho_{\text{Na}}\) is the generalized smear density of all the sodium (moving liquid, stationary liquid film, and vapor).
(14.4‑9)
where
\(\rho_{\text{Nm}}\) is the generalized smear density of the sodium vapor and the mobile liquid sodium.
(14.4‑10)
where
\(\rho_{\text{fi}}\) is the generalized smear density of the free fission gas in the channel.
(14.4‑11)
where
\({\rho'}_{\text{fv}}\) is the generalized smear density of the fuel vapor in the channel.
(14.4‑12)
where
\({\rho'}_{\text{Mi}}\) is the total generalized smear density of all moving “light components” (liquid sodium, sodium vapor, free fission gas, and fuel vapor).
(14.4‑13)
where
\({\rho'}_{\text{fs}}\) is the generalized smear density of the dissolved fission gas in the moving liquid or solid fuel.
All the variables and subscripts are described in the list of symbols at the beginning of Chapter 14. The subscript ch, op requires some additional explanation. It designates the open channel cross section which is occupied by the moving materials in the channel including the sodium film. The basic definition of \(\theta_{\text{ch,op}}\) will become clearer if one rewrites Eq. 14.3-3 with \(\theta_{\text{ch,op}}\) on the left-hand side of the equation.
In Eq. 14.4-6, the definition of the volume fractions, which is given in Eq. 14.4-1, is used to rewrite the right-hand side of this equation. The initial forms of the conservation equations described in the following sub-sections contain products of the physical densities and the cross-sectional areas associated with each component. After dividing these equations by AXMX, one can make use of the above definitions for the volume fractions and generalized linear densities to simplify the conservation equations.
For the generalized source or sink terms,
(14.4‑14)
where the source or sink terms \(S^{l}\) are the mass sources and sinks per unit time and per unit length.
14.4.2. Mass Conservation for Fuel, Sodium, and Free and Dissolved Fission-gas¶
14.4.2.1. Moving Components: Differential Equation¶
14.4.2.1.1. Fuel and Fuel Vapor Mass Conservation¶
The differential equation for the mass conservation of all the moving fuel, including fuel \(\text{vapor}^{*}\) 2 is:
(14.4‑15)
where the source terms denoted by \(S^{l}\) are the mass sources and sinks per unit time and per unit length. The source term due to fuel ejection has been discussed in Section 14.3. The source and sink terms due to fuel freeze-out and frozen fuel remelting, respectively, will be discussed in Section 14.4.3.2.
By dividing the above mass conservation equation by AXMX and by using the definitions for the generalized volume fractions and smear densities one arrives at:
(14.4‑16)
where
(14.4‑17)
is the total generalized mobile fuel smear density in the channel including solid and liquid fuel and fuel vapor. The primed source and sink terms represent the mass sources and sinks per unit time and unit volume. The latter is a m3 of the cell volume \(\text{AXMX} \cdot \Delta z\) in which all components (including pin, structure and channel components) are assumed to be uniformly smeared.
Fuel vapor streaming into regions with no fuel or with fuel which is not generating significant fuel vapor pressure (i.e., less than 10-2 MPa) is not currently considered in PLUTO2.
14.4.2.1.2. Dissolved Fission-gas Mass Conservation¶
The mass conservation for the dissolved fission gas (or matrix fission gas) in the moving liquid or solid fuel reads:
(14.4‑18)
where the fuel mass sources \(S_{\text{fu, ej}}^{l}\) and \(S_{\text{fu, ff}}^{l}\) have been multiplied by the dissolved gas-to-fuel mass ratios in the molten pin cavity and in the channel, respectively, to obtain the dissolved gas sources. The areas and densities with the subscripts fsca and fuca are for the molten pin cavity. The sink term \(S_{\text{fs, rl}}^{l}\) is the rate of dissolved fission-gas release. Its generalized form is described in Eq. 14.4-20. By dividing Eq. 14.4-18 by AXMX and by using the definitions for the generalized smear densities, one arrives at:
(14.4‑19)
(14.4‑20)
where CIRTFS is a dissolved gas release time constant which is input and has the dimensions s-1. The same gas release time constant is used for releasing the dissolved gas in the molten pin cavity (see Section 14.2.6).
14.4.2.1.3. Two-phase Sodium Mass Conservation¶
The mass conservation equation of the sodium liquid and vapor including the sodium film is given by
(14.4‑21)
where
\(\rho_{\text{Na}}\) is the total sodium smear density, including the sodium films, in the channel. Note that this is not a generalized smear density.
\(\rho_{\text{Nm,ch}}\) is the smear density of the mobile sodium referring to the cross section \(A_{\text{Nm}}\) of the moving sodium mixture.
(14.4‑21a)
where
\(A_{\text{ch}}\) is the cross sectional area of the channel;
\(A_{\text{Na,fm}}\) is the cross sectional area of the liquid Na films;
\(A_{\text{ff}}\) is the cross sectional area of frozen fuel.
By dividing the mass conservation Eq. 14.4-21 by AXMX and using the definitions for the generalized smear densities, one obtains:
(14.4‑22)
where
(14.4‑23)
The calculation of the volume fraction of the sodium film, \(\theta_{\text{fm}}\), considers vapor condensation, film evaporation and film entrainment. This is described in Section 14.4.2.2.
14.4.2.1.4. Free Fission-gas Mass Conservation¶
(14.4‑24)
where the two source terms are due to fission-gas ejection from the fuel pins and due to the release of fission gas dissolved in the fuel. The rate of fuel ejection from the pins is described in Section 14.3. The release of the dissolved fission gas is described in Eq. 14.4-20. Dividing by AXMX and using the generalized smear density definitions, one obtains:
(14.4‑25)
14.4.2.2. Finite Difference Forms of the Mass Conservations and Subroutine PLMACO¶
For the free fission gas and the dissolved fission gas, the form of the differential mass conservation is:
(14.4‑26)
where \(k\) designates a specific component and n the different types of source or sink terms for this component.
For the numerical solution of these equations, a staggered mesh with the velocities at the edges and the densities at the mesh centers is used (on the numerical grid, which is actually used in the code, the half indices have to be avoided; see later in this section).
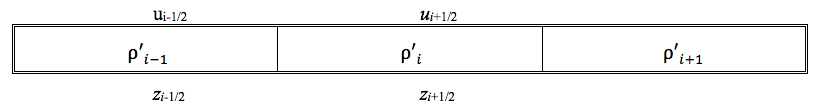
By spatially integrating over the control volume for \(z_{\text{i-1/2}}\) to \(z_{\text{i+1/2}}\) one obtains
(14.4‑27)
By performing the time integration over the length of the time step, \(\Delta t\), we obtain:
(14.4‑28)
It should be noted that this finite difference form of mass conservation is in a conservation form that prevents any mass losses. It should be noted that this mass conservation actually includes a variable flow cross-section treatment because the primed generalized smear densities include the flow cross-section areas.
Full donor cell differencing is used for evaluating the convective fluxes. Although this is not as accurate as higher order approaches, it tends to increase the stability of the solution [14-30, 14-31]. This is important because of the very complicated flow condition which can be encountered in PLUTO2 calculations. The convective terms in Eq. 14.4-28 are calculated in the following manner:
(14.4‑29)
(14.4‑30)
In the above equations, half indices are used that can be located on the previous schematic of the mesh grid. However, since half indices cannot be used in a computer program, the indices used in the code are arranged on the numerical grid as follows:
When using FORTRAN variable names, the convective flux for the free fission gas at \(i-1/2\) is therefore:
(14.4‑31)
The convective fluxes are set to zero at the edges of the component domains. The location of the upper and lower interfaces of each component domain is calculated in PLUTO2. The integers designating the lowermost and uppermost nodes containing free fission gas are designated IFFIBT and IFFITP, respectively, and the convective fluxes are set to zero at these locations:
(14.4‑32)
(14.4‑33)
Eq. 14.4-15 is the fuel mass conservation in differential form. It can be rearranged to give
(14.4‑34)
By integrating over \(\Delta z_{\text{i}}\) and \(\Delta t\), one obtains:
(14.4‑35)
In the code, the convective flux term \(\left\lbrack \left( {\rho'}_{\text{fuch}} - {\rho'}_{\text{fv}} \right) u_{\text{fu}} \right\rbrack_{\text{i-1/2}}\) is written as:
(14.4‑36)
The two-phase sodium mass conservation equation (Eq. 14.4-22) includes the generalized smear density of the moving mixture in the convective term and not the total sodium smear density which includes the sodium film. The value of the density is evaluated according to eq. 14.4-23. When using the FORTRAN variable names, the convective flux at the boundary \(i-1/2\) is:
(14.4‑37)
All of the above mass conservation equations are solved in subroutine PLMACO (PLUTO2 MASS CONSERVATION). However, sink or source terms related to fuel plateout and frozen fuel crust release are considered earlier in the calculational sequence in subroutine PLFREZ. Fuel and fission-gas ejection terms are considered later when subroutine PL1PIN, which calculates these terms, is called. Besides solving the mass conservation equations, PLMACO also contains a special treatment for the numerical cells at the bottom and top of the channel, which comes into play only when the interaction zone extends to the subassembly inlet or outlet. For example if the interaction zone has reached the subassembly outlet and if the pressure in the top node is larger than the outlet pressure, appropriate amounts of fuel, sodium and fission gas are taken out of the top nodes in order to reduce the pressure to the outlet pressure. The same procedure is performed for the inlet node if the interaction zone extends into it. The total component masses taken out of the end nodes are shown in the PLUTO2 output.
14.4.2.3. Determination of the Axial Extent of the Component Regions in Subroutine PLIF and Mesh Rezoning in Subroutine PLREZO¶
Before the above mass conservation equations are solved in subroutine PLMACO, the axial extent of the different component regions has to be determined. In subroutine PLIF (PLUTO2 INTERFACE), the interface locations of the interaction region are reset (the velocity calculations of the liquid sodium slugs above and below this region, which determine the interface velocities, are actually done later in the sequence in PLMOCO). The resetting of the interaction zone interface locations is not quite straightforward because the sodium slugs leave a liquid sodium film behind on the cladding and structure when the interaction zone expands. Because the dynamic slug calculation in PLMOCO is done for the entire channel cross section area, the interface displacement is increased by a factor of 1/(1 ‑ liquid film cross section/channel cross section). This conserves the sodium voiding calculated for the entire cross section. For a sodium slug reentering over an existing film the slug interface displacement is increased by multiplying by (1 + liquid film cross section/channel cross section). PLIF also resets the lower and upper interface locations of the fuel region which can be inside the interaction region or at the interaction zone boundaries. If the latter are being penetrated by the fuel, they are set to the fuel interfaces in subroutine PLREZO, as discussed below (the actual velocity calculation of the fuel interfaces is done in PLMOCO). Furthermore, the upper and lower interface locations of both the free fission gas and the fuel vapor region are calculated in the subroutine PLIF (these interfaces can also be at the edges of the interaction region or inside it; the velocities of these interfaces are assumed to be equal to the local sodium/fission gas/fuel vapor mixture velocities). Besides calculating the extent of the component regions, the subroutine PLIF also calculates the axial fuel‑pin failure propagation (see Section 14.3). If the fuel pins fail into the liquid sodium slugs outside the interaction zone, the interaction zone is enlarged in subroutine PLREZO. This is discussed below.
In subroutine PLREZO (PLUTO2 REZONE), mesh cells are added to an expanding interaction region or deleted from a shrinking interaction region. In the schematic below it is shown that the end cells of the interaction region can be shorter or longer than the regular cell lengths. The small cell 6 in the schematic exists because L1 is greater than the input value DZPLIN, which has to be shorter than any regular mesh cell used in a given calculation. Cell 9 is larger than the regular cell length at this location because it has not yet extended enough into cell 10 (L2 < DZPLIN). Creating a new cell or collapsing a small cell with a neighboring one is a complicated procedure because it requires redistributing liquid sodium and fission gas in a manner that no significant pressure disturbances are introduced. The SAS4A reactivity calculation refers only to the regular mesh grid and not the Lagrangian edge cells. The material in a particular cell grid such as cell No. 6 is assumed to be homogeneously mixed with the liquid sodium sluglet to the left of it for the reactivity calculation. The materials in the section L2 of cell 9 are assumed to be homogeneously mixed with cell 10 for the reactivity calculation.
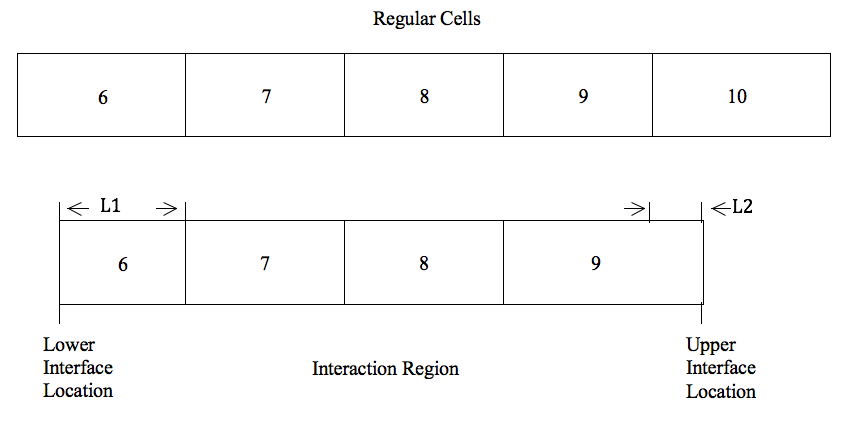
Subroutine PLREZO also expands the interaction zone when fuel penetrates the liquid sodium slugs. The liquid sodium that has been penetrated by the fuel is added to the edge cell and homogeneously distributed into it.
PLREZO also has the following treatment for slug interfaces (with the interaction region) crossing into cells that contain frozen fuel crusts or cells into which fuel can be ejected from adjacent ruptured fuel pin nodes: the liquid sodium that has crossed into such a cell is homogeneously distributed in it and the slug interface location is reset to the edge of the cell containing frozen fuel or the ejection cell, respectively.
14.4.2.4. Stationary Sodium Films and Subroutine PLVOFR¶
The liquid sodium films that are left behind by the ejected coolant slugs are of importance for keeping the cladding cool in voided regions of the coolant channel. Moreover, when fuel moves into voided regions in which a liquid sodium film is still present, the fuel‑to‑liquid sodium heat transfer will increase the liquid sodium evaporation, and thus the sodium vapor pressure.
In PLUTO2, the liquid sodium film is assumed to be stationary. It can become thinner due to sodium evaporation or to entrainment caused by the drag from the moving vapor/gas/sodium droplet/fuel particle mixture. Once an annular fuel flow regime develops in a coolant channel node, the entire sodium film in that node is added to the moving vapor/gas/sodium droplet flow (This assumption should be further investigated). Liquid sodium films can grow due to sodium vapor condensation and sodium droplet de‑entrainment, i.e., deposition on the film. However, the maximum thickness of the liquid film cannot be larger than the initial film thickness, which is determined by the input liquid film fraction CINAFO.
The evaporation of, or the condensation on, the liquid sodium film is taken into account in the sodium energy equation and contributes to the change of the liquid sodium fraction in a numerical cell. Once the liquid sodium fraction is below the input film fraction, the sodium film fraction will approach and eventually be equal to the current liquid fraction if the node considered is in the de‑entrainment mode. If the sodium film is being entrained, the sodium film thickness is determined by this mechanism.
In order to determine whether sodium entrainment or de‑entrainment occurs, the superficial velocity (i.e., the volumetric flux divided by the entire channel cross section) of the fission‑gas/two‑phase sodium/fuel particle mixture has to be evaluated. The following momentum averaging suggested by Ishii [14‑58] is performed to arrive at an average velocity of all the moving components:
(14.4‑38)
where CIETFU is an input value which can be between zero and one. This input variable has been introduced because of the uncertainty about the influence of the fuel particles on the entrainment of the film. If one assumes that the fuel particle mass can be smeared over the entraining mixture cross section and that it would act like a dense gas, \(\text{CIETFU} = 1.0\) has to be chosen. If one assumes that the fuel particles are less efficient in entraining the film, a lower value should be used. A value of 0.1 is recommended because it was used successfully in experiment analyses of TREAT tests L8 and H6 [14‑15, 14‑12].
The entrainment limit \(u_{\text{et,min}}\) used in the code is based on a correlation given in Reference [14‑33, 14‑34] for the inception of entrainment of a rough turbulent film flow:
(14.4‑39)
where the viscosity number VCONST is defined by
(14.4‑40)
\(\mu_{\text{Nl}}\) = viscosity of liquid sodium
\(\sigma_{\text{N1}}\) = surface tension of liquid sodium
\(\rho_{\text{N1}}\) = density of liquid sodium
\(\rho_{\text{Mi,fu}} = \text{CIETFU} \cdot \frac{{\rho'}_{\text{fu}}}{\theta_{\text{ch}}} + \frac{{\rho'}_{\text{Mi}}}{\theta_{\text{ch}}}\)
In the entrainment mode:
(14.4‑40a)
The amount of sodium film entrained is computed using the following equation.
(14.4‑41)
where
\(\text{CINAFO} \cdot \theta_{\text{ch,op}}\) = initial and maximum liquid sodium film generalized volume fraction (CINAFO is input);
\(\Delta t_{\text{PL}} \big/ \left( 5 \text{ ms} \right)\) = fraction of the initial and maximum film volume fraction which is entrained during a PLUTO2 time step.
The entrainment time constant of 5 milliseconds will lead to a complete entrainment of the liquid film in 5 milliseconds if the mixture velocity stays above the entrainment limit during that time. Since the entrained liquid sodium droplets are assumed to be instantaneously in velocity equilibrium with the moving mixture, the velocity of the latter can decrease due to the entrainment. This may temporarily lead to a de‑entrainment period, which is characterized by:
and
(14.4‑42)
Subroutine PLVOFR. Subroutine PLVOFR (PLUTO2 VOLUME FRACTIONS) calculates the sodium entrainment/de‑entrainment discussed above. Two other tasks are performed in this routine. One is concerned with the setting of most channel volume fractions and the other with the selection of the fuel flow regimes. The latter will be discussed in the next section.
Since PLVOFR is called after PLMACO and PLFREZ, the volume fractions calculated in PLVOFR already reflect the component mass changes due to convection and due to fuel plateout and fuel crust release. Volume fractions set in this routine include the moving fuel volume fraction \(\theta_{\text{fu}}\), the volume fraction of the open channel \(\theta_{\text{ch,op}} = \theta_{\text{ch}} - \theta_{\text{ff}}\), the liquid sodium volume fraction \(\theta_{\text{Nl}}\), the vapor/gas volume fraction when the liquid sodium is assumed to be uncompressed \(\theta_{\text{vg,un}}\), the vapor/gas volume fraction for properly compressed liquid sodium \(\theta_{\text{vg}}\), and also the sodium film volume fraction \(\theta_{\text{fm}}\) as discussed above. Moreover, the sodium quality is calculated in this routine. It is based on the following definition:
(14.4‑43)
The last equation can be solved for \(x_{\text{Na}}\):
(14.4‑44)
where
The sodium void fraction is also set in PLVOFR. It is based on the definition
(14.4‑45)
This leads to
(14.4‑46)
The volume fraction of the vapor/gas mixture for the case of uncompressed liquid sodium is
(14.4‑47)
The gas/vapor volume fraction for compressed liquid sodium is
(14.4‑48)
where
\(K_{\text{N1}} = \text{CMNL}\) which is a single input value for the isothermal liquid sodium compressibility.
The \(\theta_{\text{vg}}\) calculated in this routine is not allowed to be smaller than \(\frac{\theta_{\text{ch,op}}}{1000}\). This is done because \(\theta_{\text{vg}}\) is used in the denominator of certain interaction terms. Later in the fission-gas pressure calculation in subroutine PLNAEN, the \(\theta_{\text{vg}}\) is implicitly used without the above-mentioned restriction.
14.4.3. Fuel Flow Regimes, Fuel Plateout and Frozen Crust Release, Plated‑out and Moving Fuel Configurations, and Energy and Momentum Exchange Terms¶
14.4.3.1. Fuel Flow Regimes¶
Based on the evidence from TREAT TOP experiments, only a fraction of the fuel ejected into the coolant channels fragments into particles or droplets that get rapidly swept upwards. The other fuel does not break up but moves in the channels in the form of a continuous flow that tends to plate out on the cladding and structure upon freezing. Particulate debris with only little plated‑out fuel was found in TOP tests R12 [14‑35] and J1 [14‑25] in which the power transients were cut soon after the first indication of pin failure. This suggests that the fuel that is ejected first from the pins and contacts liquid sodium tends to break up. The fuel that is ejected later into a locally voided channel tends to stay together although liquid sodium reentering from below can cause a delayed fragmentation. This was concluded from the analysis of TREAT test H4 [14‑37, 14‑36].
The CAMEL out‑of‑pile tests [14‑38, 14‑39] also show rapid particulate fuel sweepout. The fuel that does not fragment tends to plate out very close to the fuel ejection site in these out‑of‑pile tests. The regions with plated-out fuel found in the post‑test examination of most TREAT TOP tests, however, extend considerably above the cladding failure site. This indicates the temporary existence of a continuous fuel flow in TREAT experiments. The likely reasons why the plated‑out fuel does not extend further upwards in CAMEL tests are (a) the lack of continued fission heating of the fuel in these out‑of‑pile tests, (b) the amount of fuel ejected into the channels in these tests was relatively small, and thus, had little stored heat, and (c) the relatively cold cladding and structure in these tests may rapidly cool the fuel. Two further items may have promoted the rather localized plateout in the CAMEL tests. First, the ejection of the thermite fuel in several CAMEL tests was accompanied by excessive amounts of gas. Second, the CAMEL ejection pressure was high for longer times than expected for fuel ejection from prototypic pins. Both these items cause coolant channel voiding and lack of fragmentation.
In PLUTO2, one particulate and two continuous fuel flow regimes are modeled. The latter include annular flow (which can be a total or a partial annular flow) and bubbly flow. Flow regime in a cell is determined based on flow conditions in that cell, and can vary from cell to cell. All possible PLUTO2 flow regimes are depicted in Figure 14.4.1. The use of these flow regimes has the advantage of providing a geometry which allows a more straighforward determination of the mass, momentum, and energy exchange terms than in models not explicitly treating different flow regimes.
The particulate or droplet flow regime has been traditionally assumed in fuel‑coolant interaction (FCI) models such as the Cho‑Wright model [14‑9], the Board‑Hall model [14‑40], and the MURTI model [14‑41]. Whole‑core modules assuming particulate flow include the SAS/FCI module of SAS3D [14‑1] and the EPIC code [14‑7, 14‑8] which has been coupled with the SAS3D code. It is also interesting to note that the SIMMER‑II disassembly and transition phase code [14‑29] treats all its moving liquid or solid components as droplet or particulate flows. However, some attempts are made to account for the effect of flow regimes on exchange terms.
The PLUTO code [14‑3, 14‑4], which is the predecessor of PLUTO2, assumed exclusively particulate or droplet flow. It was nevertheless successful in analyzing the fuel motion and sodium voiding during the first few tens of milliseconds after pin failure in the E8 $3/s TOP experiment [14‑5, 14‑6] and also the fuel motion and voiding during the first event of the H6 $0.5/s TOP experiment [14‑6].
The particulate flow regime has therefore been retained in PLUTO2. The fuel ejected into liquid sodium is assumed to instantaneously fragment into droplets or particles of radius RAFPLA if the liquid sodium fraction \(\theta_{\text{N1}} > \text{VFNALQ} \cdot \theta_{\text{ch, op}}\). Both RAFPLA and VFNALQ are input. All particles can, later on, simultaneously further fragment (after an input time delay of TIFP after pin failure) into smaller particles with radius RAFPSM, which is also input. Moreover, if the liquid sodium fraction in a certain channel node exceeds the input value VFNARE, mobile fuel, which was previously in a continuous flow regime (i.e., annular or bubbly flow), will instantaneously fragment into droplets in this node. This is an attempt to simulate delayed FCIs generated by sodium slugs reentering from below.
The continuous fuel flow regime in PLUT02 will develop if considerable local voiding has occurred \(\left(\theta_{\text{N1}} < \text{VFNALQ} \cdot \theta_{\text{ch, op}} \right)\) and if the fuel energy is above the input fuel energy EGMN. For the latter a value somewhat above the solidus energy is suggested. This is because particles with an average energy corresponding to the solidus may already have a frozen outer crust which will prevent them from splattering on cladding and will thus not lead to an annular film flow. For the input value VFNALQ, which is the liquid sodium fraction below which a continuous fuel flow can develop, a value of 0.33 is recommended because it was used in the successful L8 post‑test analysis [14‑15, 14‑12].
Once a continuous fuel flow has developed and is not yet occupying most of the coolant channel open cross sectional area at a certain elevation, a partially or fully annular fuel flow regime is assumed at that elevation. The partially annular flow regime was introduced because it appears unlikely that a relatively small amount of liquid fuel would spread around the entire perimeter of the coolant channel (see Eq. 14.4-74). Once the fuel volume fraction at a certain axial elevation becomes higher than the input value CIBBIN (for which a value of 0.7 is recommended), the development of a bubbly fuel flow is assumed to occur. This bubbly flow is then assumed to exist until the fuel volume fraction drops below 2/3 of the input volume fraction CIBBIN. This is because surface tension effects can maintain the bubbly flow down to a lower fuel volume fraction compared to the value required to cause the onset of the bubbly flow. The decision about flow regime changes is made at the end of subroutine PLVOFR. The logic flow for deciding whether the flow regime in a certain node should remain the same or whether it should change to another one is shown in Figure 14.4.4. The sequence of “if” checks and statements is exactly the same as in the program. The input parameters appearing in the flowchart have already been described above. The meaning of the Flow Regime [F.R.] numbers is the following:
F.R. 1 particulate or droplet flow regime
F.R. 3 partially or fully annular fuel flow
F.R. 4 bubbly fuel flow
The flow regime labels for each node i are stored in the code in pointer array IFLAG(I). The value 2 has been reserved for a possible future PLUTO2 version in which cladding motion is considered and in which the number 2 would designate nodes with moving cladding. In the LEVITATE module, flow regime 2 is operational and designates molten cladding flow with imbedded fuel drops or chunks.
In explaining the flow chart logic, it is best to start at the time of PLUTO2 initiation when the flow regime in all nodes is set to 1 (particulate flow). The fuel will remain in flow regime 1 at least until the fourth diamond from above leads to a “no”. However, if the fuel particles are already cold enough, the third diamond from above will keep them in particulate form. If both the third and fourth diamond lead to “no”, the logic flow will drop straight through, lead to a complete entrainment of the liquid sodium film in the node considered and then switch to the annular flow regime (F.R. = 3). If the lowermost diamond leads to a “no”, a switch to the bubbly flow regime (F.R. = 4) will be made. If such a switch occurs, the vapor/gas/sodium droplets mixture velocity will be set to the fuel velocity. This is done at the moment of bubbly flow regime initiation only. This helps to initialize a well‑behaved two‑fluid bubbly flow calculation. Starting with the previous vapor/gas/sodium droplets mixture velocity from the annular flow, which can be fairly high, can cause problems with the inertial terms in the bubbly flow calculation.
Once an annular or bubbly flow regime has been established in a node, the only way to get back to the particulate or droplet regime is via the first diamond. The latter will make it a particulate flow only if enough liquid sodium has reentered into the node considered. Once a bubbly flow regime has been established, it will get back to the annular flow regime only if the second lowest diamond leads to a “no”. Overall, it has been attempted to keep the numerical nodes in the same flow regime for a reasonable length of time. This has helped to stabilize the overall calculation.
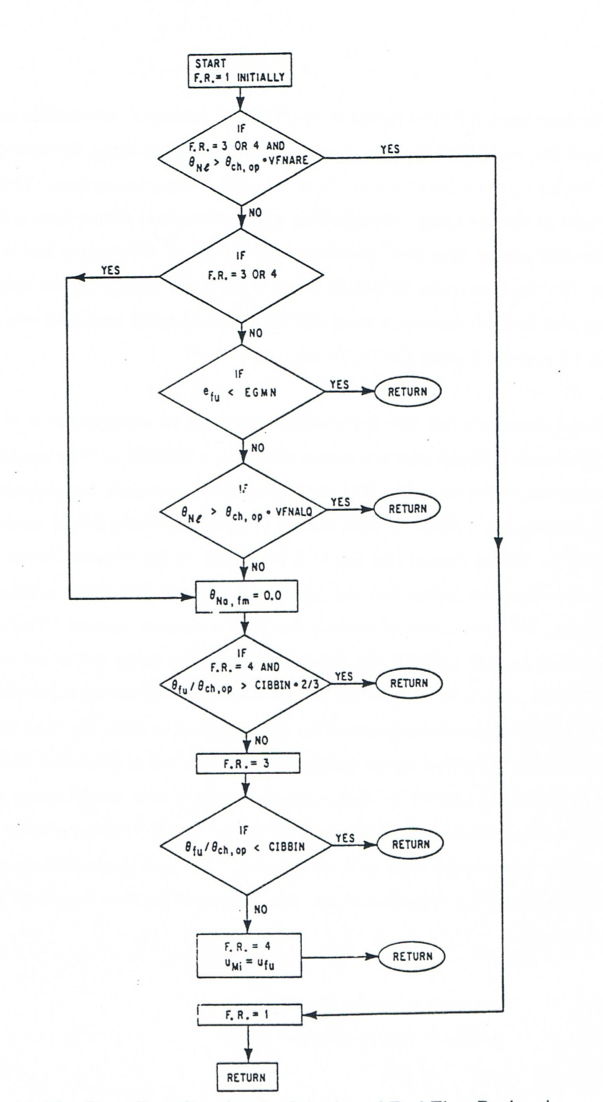
Figure 14.4.4 Flow Chart Showing the Selection of Fuel Flow Regime in a Coolant Channel Mesh Cell¶
14.4.3.2. Fuel Plateout and Frozen Fuel Crust Release in Subroutine PLFREZ¶
In subroutine PLFREZ (PLUTO2 FREEZING ROUTINE), the amount of fuel plating out on cladding and structure as well as the amount of frozen fuel crust released from an underlying melting cladding are calculated. This information is later used in subroutine PLMISC to update the frozen fuel geometry. PLFREZ is called before the mass conservation equations and it can therefore provide updated densities and velocities of the moving components for the mass conservation. (The velocity change of the moving mixture due to frozen crust release is calculated in PLFREZ). However, since PLFREZ uses data from the end of the last time step, it could also have been called at the end of the calculational sequence as it is done in LEVITATE.
Fuel plateout on the cladding and structure of channel node i can only occur if there is either an annular or bubbly fuel flow regime in that node. Solid particles or particles with a reasonably thick solid outer crust are not believed to be able to stick to a cold surface, and molten droplets can exist in PLUTO2 only if there is a significant liquid sodium volume fraction (\(\theta_{\text{N1}} > \text{VFNALQ} \cdot \theta_{\text{ch, op}}\); see previous section). The liquid sodium and, in particular, the liquid sodium film are assumed to prevent molten fuel droplets from sticking to cold surfaces because the droplets should form thin solid crusts due to the contact with the liquid sodium. The assumption that liquid droplets which are surrounded by significant amounts of liquid sodium will not plate out on cold surfaces may be questionable when a jet of fuel droplets hits a cold wall with a reasonably high velocity. In this case, the droplets may splatter on the cold wall and form a moving liquid film, which soon freezes and sticks despite the presence of liquid sodium. Such a high‑velocity impingement of fuel may have occurred in the P4 test [14‑42] or during the later stages of some of the CAMEL tests [14‑38, 14‑39]. This high‑velocity impingement is not modeled in PLUTO2, but its effect can be roughly simulated by using for the input value VFNALQ, which is the sodium liquid fraction above which droplet or particle flow is allowed, a value close to 1, and for the input value VFNARE, also a value close to 1 and greater than VFNALQ. In the P4 pre‑test analysis with PLUTO2, VFNALQ = 0.33 was used (similar values had been used in the successful PLUTO2 analyses of H6 [14‑6] and L8 [14‑15, 14-12]). This input choice led to the prediction of total fuel sweepout because only flow regime 1 (particulate or droplet flow) was selected by the code. The P4 experiment, however, showed extensive plateout and little sweepout. The above explanation of a high‑velocity fuel jet hitting the cladding, however, is not the only possible explanation. Another explanation for this preferential plateout may be that the sodium could have bypassed the ejected fuel in this relatively large bundle test and, therefore, not exerted the full inlet pressure on it.
To be in the annular or bubbly flow regime is only one of the necessary conditions for initiating plateout. The other ones are:
(14.4‑49)
and
(14.4‑50)
and
(14.4‑51)
and
(14.4‑51a)
Moreover, the moving fuel volume fraction is not allowed to drop below 0.01 of the channel volume fraction due to fuel plateout. This is done to avoid problems with zero amounts of moving fuel.
The condition 14.4-49 states that the moving that the moving fuel energy should be below the input value EGBBLY which has to be within the melting band of the fuel. A value in the lower part of the melting band is recommended, based on the L8 analysis with PLUTO2 [14‑15, 14‑12]. One should be careful that the input value EGMN, below which a continuous flow regime cannot develop (see Figure 14.4.4), is smaller than EGBBLY because this can inhibit plateout.
The condition 14.4‑50 states that the temperature of the fuel crust on the cladding should be below the fuel solidus temperature in order to allow plateout. Fuel should not plate out on already molten fuel crusts (layers), and, as soon as the fuel crust temperature has increased half way into the melting band, this fuel crust will actually be ablated by the moving fuel field (see below).
The condition 14.4‑51 states that fuel plateout will occur only if the cladding surface temperature is less than the input value TECLMN. This value should be set to the steel solidus temperature TESOL (which is input) or somewhat above it. It is believed that freezing fuel will not stick to a molten cladding surface but rather slide over it. However, it will probably also ablate some of the molten steel which is not treated in PLUTO2. If one wants to consider this phenomenon, one will have to switch to the LEVITATE module, which is treating steel ablation. This can be done by setting the input value NCPLEV to a low integer number.
The condition 14.4‑51a limits the frozen fuel fraction in a node to 70% of the nodal volume. Thus a complete plugging of a coolant channel is not allowed in PLUTO2. This is done because the PLUTO2 equations are written for relatively smoothly varying flow cross sections. If all the above‑mentioned conditions are met in a channel cell, then fuel plateout will occur in that cell. There are two possibilities:
If
the amount of mobile fuel which will be plated out in node \(i\) during \(\Delta t_{\text{PL}}\) is calculated from:
(14.4‑52)
The input parameter (EGBBLY) appeared already in Eq. 14.4-49. It has to be between the fuel solidus and liquidus energies. The latter are the input values EGFUSO and EGFULQ, respectively. It was mentioned earlier that a value in the lower part of the melting range is recommended based on the PLUTO2 L8 analysis [14‑15, 14‑12]. The fuel which plates out is assumed to have a temperature of
(14.4‑53)
This assumption leads to a temperature increase of the mobile fuel when plateout occurs and is accounted for in the code. The underlying assumption is that the mobile fuel has a radial temperature gradient with the freezing fuel being at the fuel solidus temperature.
If
the fraction of the mobile fuel plated out in a PLUTO2 time step of \(\Delta t_{\text{PL}}\) second will be calculated from
(14.4‑54)
which causes a near complete fuel plateout of the mobile fuel in \(2 \text{ ms}\). This situation can occur when frozen fuel crusts, which were released in another cell due to melting cladding, slide into a cell in which cladding has not yet melted. The assumption is that these fuel crusts will bring with them some liquid steel that will make them stick on still‑unmelted cladding. The temperature of the plated‑out fuel in this case equals the temperature of the moving fuel.
(14.4‑55)
For both cases, the temperature changes of the frozen fuel crusts on cladding and structure are calculated in the same way by making use of the assumptions about \(T_{\text{fu, fz}}\) in Eqs. 14.4-53 and 14.4-55.
(14.4‑56)
and
(14.4‑57)
Because the relative fractions of the fuel plating out on cladding and on structure and the relative fractions of fuel already plated out on cladding and structure are assumed to be the same, the above two equations are very similar. This is because the fraction of the fuel plating out on cladding cancels out in Eq. 14.4-56, and the fraction of fuel plating out on the structure cancels out in Eq. 14.4-57. Although separate temperatures for the frozen film on the cladding and structure are tracked in PLUTO2, only one common smear density is tracked for the frozen films. This should be improved in a future PLUTO2 version.
When fuel plateout has occurred, the generalized densities of the mobile and frozen fuel, the generalized volume fractions \(\theta_{\text{ch,op}}\), \(\theta_{\text{fu}}\), and \(\theta_{\text{vg}}\) of the open channel, mobile fuel, and the vapor/gas mixture are updated. Moreover, the channel hydraulic diameter is updated:
(14.4‑58)
This change in the hydraulic diameter is based only on the changes in the open channel cross‑section area because the perimeter of the open channel will remain approximately the same whether a fuel crust is present or not. This is a reasonable approximation for an actual subchannel, but it would not be good for a cylindrical pipe.
Fuel crusts can also be released and added back into the moving fuel field. One apparent reason is that the fuel crust can become re‑melted due to fission heating and/or the heat flux from the moving fuel. In the code, the crust release due to remelting is initiated when the fuel crust temperature is half way through the melting band. The fraction CFMELT of the crust released per PLUTO2 time step is calculated from:
(14.4‑59)
The new generalized smear density of the fuel crust is
(14.4‑60)
where
(14.4‑61)
A melting fuel crust is assumed to have a higher temperature at the interface with the gas/vapor mixture than at the interface with the cladding because the cladding cannot be significantly molten since this would have led to crust ablation (see below). Therefore the crust thickness is reduced in this case of crust melting:
(14.4‑62)
The other reason for releasing a fuel crust in PLUTO2 is the melting of the underlying cladding. The frozen fuel crust in mesh cell \(i\) will be released in PLUTO2 when the temperature of the middle cladding node has exceeded the input value TECLRL in cell \(i\). A value in the upper part of the cladding melting band is recommended. The frozen crust is rapidly released in this case according to
(14.4‑63)
This means that a crust which would initially fill the entire channel would be completely released in 5 ms. A crust occupying only a fraction \(\text{FN}_{\text{ff}}\) of the channel would be released in \(\text{FN}_{\text{ff}} \cdot 5 \text{ ms}\). The change in the generalized densities of the fuel crust and also the mobile fuel are calculated with Eqs. 14.4-60 and 14.4‑61. In this case of frozen crust release, it is likely fuel pieces with the full crust thickness will get released and that only the fraction of the channel perimeter, which is covered by frozen crust, which is CFFFCL, gets reduced:
(14.4‑64)
It is important to note that the treatment of frozen crust release after the underlying cladding has melted and also the disallowing of fuel plateout on molten cladding made the successful L8 post‑test analysis with PLUTO2 possible [14‑15, 14‑12]. In the pre‑test analysis, these phenomena were not considered and led to a considerable underprediction of the fuel dispersal [14‑43, 14-16]. The current treatment, however, is not yet ideal because the released frozen crust pieces are homogenized with the mobile fuel in the node considered. Ideally, these frozen fuel pieces should be treated in a separate chunk field. Such a treatment is being incorporated in the chunk version of the LEVITATE module. Once this version has been made compatible with the SAS4A release version, one can switch to it via the NCPLEV input parameter. This input parameter specifies the number of axial cladding nodes which have to be fully molten before a switch from PLUTO2 to LEVITATE occurs.
For both the remelting of a crust and the release of a frozen crust, energy and velocity adjustments for the moving fuel are made in the lower section of subroutine PLFREZ. Although these adjustments could also be made later in the fuel energy and momentum equations, it is easier to do it in this subroutine because several local variables that are needed would have to become part of the common blocks. The energy adjustment for the moving fuel is:
(14.4‑65)
where
The calculation of the velocity adjustments for the moving fuel at the lower and upper boundaries of the mesh cell \(i\) is as follows:
(14.4‑66)
(14.4‑67)
If the release of a fuel crust has taken place, the generalized volume fractions \(\theta_{\text{ch,op}}\), \(\theta_{\text{fu}}\), and \(\theta_{\text{vg}}\) of the open channel, the mobile fuel, and the vapor/gas, respectively, are updated at the end of subroutine PLFREZ. Moreover, the hydraulic diameter of the channel is updated
(14.4‑68)
This change in the hydraulic diameter is based only on changes in the open channel cross‑section area because the perimeter of a real sub‑channel will be approximately the same whether a fuel crust is present or has been released.
14.4.3.3. Plated‑Out and Moving Fuel Configurations¶
The different configurations of the plated‑out and moving fuel in PLUTO2 are shown in Figure 14.4.1 at the beginning of Section 14.4.1. These configurations are shown in a cylindrical geometry although the areas and wetted perimeters used in the code are based on the actual subchannel values. The outer perimeter of the cylindrical channel shown in Figure 14.4.1 represents mostly cladding but also some structure. The various fuel configurations are of importance for calculating the energy and momentum exchange terms because the interface areas are largely determined by the fuel configurations. The fuel flow regime selection has already been described in Section 14.4.3.1. In the present section, the assumptions about the specific fuel configuration in each flow regime are described. In the code, these are implemented near the front of subroutine PLMISC (PLUTO2 MISCELLANEOUS).
In the particulate flow regime [see configuration (a) in Figure 14.4.1], the only assumption is that the particles are uniformly distributed in a numerical cell. With regard to the heat transfer between fuel and liquid sodium, both the liquid sodium film and the sodium droplets are also assumed to be uniformly distributed. The heat‑transfer area between fuel and liquid Na per unit of generalized smear volume is assumed to be
(14.4‑69)
where
\({N'}_{\text{Pa}} = \frac{{\rho'}_{\text{fu}}}{\frac{4}{3} \pi r_{\text{Pa}}^{3} \rho_{\text{fu,sol}}}\), number of fuel particles in a generalized smear volume
\(\theta_{\text{N1}}\) = the generalized liquid sodium volume fraction which includes the moving sodium droplets and the static sodium film.
CIA2 = input constant (see Eq. 14.4-98).
The heat‑transfer area between fuel particles and the vapor/gas mixture is:
(14.4‑70)
For the continuous flow regimes [see (b) through (e) in Figure 14.4.1], the assumed interaction areas between the various components are considerably more complicated than for the particulate flow regime. Several important Fortran variables describing the different configurations for continuous fuel flow will be explained first.
(14.4‑70a)
where ARCH is the coolant channel cross section area associated with one pin. AXMX has already been described in Section 14.4.2.1. NPIN is the number of pins per subassembly. Both \(\text{AXMX}\) and \(\text{NPIN}\) are input.
(14.4‑71)
where ARMF is the cross‑sectional area of moving fuel associated with one pin.
(14.4‑72)
where ARFF is the cross‑sectional area of plated‑out fuel which is associated with one pin.
(14.4‑73)
where PECH is the channel perimeter associated with one pin. This also includes a fraction of the structure perimeter. The quantities ARCL’ and ARSR’ are the cladding and structure surface areas per unit of generalized smear volume. Moreover, they are also the total perimeters of the cladding and structure (times one meter) in a unit of generalized smear volume.
The fraction of the cladding and structure which is covered by either molten or plated‑out fuel, CFFUCL, has the value 1.0 in the bubbly flow regime. In the annular flow regime (see b,c, and d in Figure 14.4.1), CFFUCL is taken to be a linear function of the total (moving fuel + fuel crust) fuel volume fraction.
(14.4‑74)
or if CFFUCL calculated from Eq. 14.4-74 is greater than 1.0:
(14.4‑74a)
The latter value applies to condition d in Figure 14.4.1. The input parameter CIANIN in Eq. 14.4-74 determines the fuel volume fraction above which a complete annular fuel flow will exist (i.e., condition d in Figure 14.4.1). A value of 0.5 is recommended, based on the L8 TREAT test analysis with PLUTO2 [14‑15, 14‑12].
In the annular flow regimes, the thickness TKFU of the layer containing both moving and plated‑out fuel is also important. Its calculation is based on the conservation of fuel volume:
(14.4‑75)
The frozen fuel crust, which is important in both the annular and the bubbly flow regimes is also characterized by two variables. These are the frozen fuel crust thickness TKFF and the fraction CFFFCL of the channel perimeter that is covered by frozen fuel crust. Both TKFF and CFFFCL are permanent arrays in the code (which are updated during the time steps), whereas the thickness and coverage fraction of the layer including all the fuel are recalculated every PLUTO2 time step. The calculation of the change in the frozen fuel cross‑sectional area due to remelting or release has been described in the previous section. The change of the frozen fuel cross section due to freezing can cause both an increase in the frozen crust thickness TKFF and in the coverage fraction CFFFCL. How much either one increases depends on whether bulk type freezing or conduction‑limited freezing [14‑44, 14-45, 14‑46] is more appropriate. In PLUTO2 the mode of plateout of fuel for the partially annular, totally annular and bubbly flow regime is controlled by an input parameter (CIFUFZ) which allows both extremes or values anywhere between these two extremes. The increase in the crust thickness is calculated from:
(14.4‑76)
where
\(\Delta \text{ARFF}\) = the change in the frozen fuel cross section during one PLUTO2 time step.
CFFFCL = the fraction of the channel perimeter covered by plated‑out fuel at the beginning of the PLUTO2 time step.
CIFUFZ = an input parameter whose value should be between 0 and 1.0. A value of zero leads to pure bulk‑type freezing (i.e., the crust grows till it reaches the thickness of the total molten fuel layer thickness before the coverage fraction CFFFCL increases). A value of 1 leads to a conduction‑type freezing. \(\text{CIFUFZ} = 0\) was used in the L8 analysis [14‑15, 14‑12] because no other option was available at that time.
and the moving fuel‑to‑frozen‑fuel heat flux per unit temperature difference and per unit of generalized smear volume is given by
(14.4‑76a)
where
\(h_{\text{fu,ff}}\) = the heat-transfer coefficient between molten fuel and frozen fuel which takes the resistance in the fuel crust into account. It is described in the following section on exchange terms.
(14.4‑77)
In Eqs. 14.4-76a and 14.4-77, CFMFFF is the fraction of the frozen crust that is assumed to be covered with moving fuel. In the bubbly flow regime, CFMFFF is always 1.0. The moving fuel-to-cladding heat flux required in Eq. 14.4-76 is given by
(14.4‑78)
where
\(h_{\text{fu,cl}}\) is the heat-transfer coefficient between moving fuel and cladding, which is described in the following section on exchange coefficients.
The initialization of the crust thickness during the first time step when plateout commences is also affected by the input parameter CIFUFZ that was discussed above:
(14.4‑79)
where the first term on the right-hand side would lead to the maximum initial crust thickness for \(\text{CIFUFZ} = 0\) and the second term gives the minimum thickness if \(\text{CIFUFZ} = 1\). The latter will cause the frozen fuel coverage fraction of the channel perimeter (CFFFCL) to be the same as the one for the total (moving + frozen) fuel, CFFUCL. Since TKFF and CFFFCL are permanent arrays in the code, the initial values of these variables are quite important. The frozen fuel coverage fraction of the channel perimeter is calculated, based on frozen fuel volume conservation:
(14.4‑79a)
If \(\text{CFFFCL} > \text{CFFUCL}\), \(\text{CFFFCL}\) and \(\text{TKFF}\) will be:
(14.4‑79b)
and
(14.4‑79c)
The crust dimension calculations described above hold in all continuous flow regimes.
14.4.3.4. Energy and Momentum Exchange Terms in Subroutine PLMISC¶
Besides calculating the moving and frozen fuel configurations, subroutine PLMISC (PLUTO2 MISCELLANEOUS) also calculates many heat-transfer and friction coefficients that are later used in the calculation of the fuel energy equations, the sodium energy equation, and in the channel momentum equation. The latter also requires several drag coefficients which are determined in the subroutine calculating the channel momentum equation, PLMOCO. However, some of the variables needed for the drag coefficients are also calculated in subroutine PLMISC.
Several heat and momentum exchange terms described below are still in a simplified or preliminary form. Additional validation efforts, which are outlined in the SAS4A validation plan [14-10], will be necessary to improve certain heat and momentum exchange terms. However, the reasonably successful analyses of TREAT experiments L8 and H6 [14-15, 14-12, 14-6] may be an indication that all of the more important exchange terms are treated properly.
14.4.3.4.1. Heat-transfer and Momentum Exchange Terms Between Sodium and Cladding, and Sodium and Structure¶
14.4.3.4.1.1. Near-Liquid Sodium¶
If \(\alpha_{\text{Na}} < \text{CIVOID}\), where CIVOID is an input parameter, liquid single-phase correlations will be used if there is still cladding or structure that is not covered by fuel (i.e., particulate or partially annular fuel flow). The input parameter CIVOID determines the sodium void fraction below which these correlations will be used. A value of 0.5 is recommended based on the L8 analysis [14-15, 14-12]. The heat-transfer coefficient that is used for low-void fraction sodium flow which has a low Prandtl number of about 0.005, is based on Ref. 14-47.
(14.4‑80)
where all variables without axial indexes are calculated at the center of cell \(i\)
\(C1, C2\) and \(C3\) are input constants, and
\(k_{\text{N1}} = \text{CDNL}\) which is a constant input value for the liquid sodium thermal conductivity
\(C_{\text{p,N1}}\) = liquid sodium heat capacity whose temperature dependence is described in the material property section of Chapter 12.
\(D_{\text{n1}} = D_{\text{ch}} \cdot \frac{\theta_{\text{N1}}}{\theta_{\text{ch, op}}}\) is the hydraulic diameter for the liquid sodium which is assumed to be in an annular flow regime.
\(D_{\text{ch}}\) = hydraulic diameter of the open coolant channel which takes the presence of a fuel crust into account (see Eq. 14.4-58)
\(\text{CFNACL}\) = fraction of the channel perimeter that is wetted by sodium. When the particulate flow regime exists, a fraction of the perimeter can be covered by frozen fuel. The value of CFNACL is in this case
(14.4‑80a)
If an annular flow regime exists
(14.4‑80b)
The CFNACL should actually be lumped together with the heat-transfer area. However, to lump such terms together with heat-transfer coefficients has the advantage that the total heat flow rates, which are calculated at the end of subroutine PLMISC, include only the total cladding or structure areas.
The heat-transfer coefficient between low-void fraction sodium and the structure is set equal to that between low-void fraction sodium and cladding
(14.4‑81)
The friction factor used for the low-void fraction sodium and fission-gas mixture is:
(14.4‑82)
where
\(\text{AFR}\), \(\text{BRF}\) are input constants
\(\text{Re}_{\text{Mi}}\) Reynolds number of the mixture of sodium and fission gas which is calculated from:
(14.4‑83)
where the viscosity of the two-phase mixture is evaluated from a formulation suggested by Dukler [14-48]:
(14.4‑83a)
where
\(\mu_{\text{Nl}}\) = VINL, viscosity of liquid sodium which is input
\(\mu_{\text{vg}}\) = VIVG, viscosity of the vapor/gas mixture which is input.
\(x_{\text{Mi}} = \frac{\left( \theta_{\text{vg}} \rho_{\text{Nv}} + {\rho'}_{\text{fi}} \right)}{{\rho'}_{\text{Mi}}}\) quality of moving sodium fission-gas mixture
\({\rho'}_{\text{Mi}} = {\rho'}_{\text{Na}} - \rho_{\text{Nl}} \theta_{\text{Na, fm}} + {\rho'}_{\text{fi}}\)
i.e., \({\rho'}_{\text{Mi}}\) is the generalized smear density of the moving sodium and the fission gas.
14.4.3.4.1.2. Liquid Sodium Films Present and a Vapor/Gas Mixture or Two-phase Sodium/Gas Mixture in the Gas Core¶
If \(\theta_{\text{Na, fm}} > 0\) and \(\alpha_{\text{Na}} > \text{CIVOID}\),
liquid sodium film evaporation or condensation on the liquid film will take place. A splitting of the currently available liquid film volume fraction, \(\theta_{\text{Na, fm}}\), into a film volume fraction for the cladding, \(\theta_{\text{cl, fm}}\), and for the structure, \(\theta_{\text{sr, fm}}\), is done in the following way:
(14.4‑84)
(14.4‑84a)
where \(\text{CINAFO}\) is an input constant which gives the initial and maximum film volume fraction. However, if \(\theta_{\text{cl,fm}} \leq 0\),
(14.4‑84b)
This means, that the structure film has its maximum value as long as a liquid film exists on the cladding. If \(T_{\text{Na}} > Tl_{\text{cl,os}}\)
(14.4‑85)
where
\(\text{CFNACN}\) is the sodium condensation coefficient which is input
and for
\(\text{CFFFCL}\) see Eq. 14.4-76
If \(T_{\text{Na}} < T_{\text{cl,os}}\)
(14.4‑86)
where
CFNAEV is the sodium evaporation coefficient which is input and which should be larger than CFNACN which is discussed above
\(w_{\text{cl,fm}}\) is the thickness of the sodium film on the clad
CDNL liquid sodium conductivity which is input
The sodium-to-structure heat-transfer coefficient, \(h_{\text{Na,sr}}\), is set equal to the \(h_{\text{Na,cl}}\) calculated from Eq. 14.4-86 as long as the structure has a lower temperature than the sodium. In the unlikely case that the structure is hotter than the sodium, an equation similar to Eq. 14.4-86 is used but with the structure film thickness, \(w_{\text{sr,fm}}\), instead of \(w_{\text{cl,fm}}\).
The friction factor for the case when liquid sodium films are present is based on Ref. 14-49, page 320, and is calculated in the following way:
(14.4‑86a)
where
\(\text{AFRV}\) and \(\text{BFRV}\) are input constants
\(\text{Re}_{\text{Mi}}\) Reynolds number for the sodium/gas mixture (see Eq. 14.4-83)
14.4.3.4.1.3. No Sodium Films Left and Sodium Temperature Below the Outer Cladding Temperature¶
This condition is common in the annular fuel flow regime in which liquid sodium films are not allowed. Moreover, in the particulate flow regime, the sodium films may have been completely entrained or evaporated. Two conditions have to be considered. First, there can be a flow of sodium droplets, vapor, and gas in the coolant channels or just a flow of vapor and gas. For void fractions larger than the input value CIA4 (which has to be larger than the input value CIVOID), the heat-transfer coefficient used is a linear interpolation between a convective heat-transfer coefficient for a pure vapor/gas moisture, \(h_{\text{vg, cl}}\), and a boiling heat-transfer coefficient HCCLMI which is input. For void fractions smaller than CIA4 and larger than CIVOID, a constant value is used:
(14.4‑87)
where
CFNACL is the fraction of the channel perimeter which is in contact with the two-phase sodium (see also Eq. 14.4-88)
HCCLMI is an input heat-transfer coefficient describing the forced convection heat transfer between sodium droplets and cladding. HCCLMI should be definitely smaller than the evaporation coefficient CFNAEV and probably also smaller than the condensation coefficient CFNACN. It should also be remembered here that for sodium void fractions less than the input value CIVOID, a single-phase convective heat-transfer coefficient is used for the calculation of \(h_{\text{Na, c} l}\) (see Eq. 14.4-80). Therefore, CIA4 should be larger than CIVOID.
For \(\alpha_{\text{Na}} > \text{CIA4}\), the above-mentioned linear interpolation is done:
(14.4‑88)
where
\(\alpha_{\text{Na}} = \frac{\left( \theta_{\text{ch, op}} - \theta_{\text{N1}} - \theta_{\text{fu}} \right)}{\left( \theta_{\text{ch, op}} - \theta_{\text{fu}} \right)}\)
\(\text{HCCLMI}\) = input heat-transfer coefficient (see Eq. 14.4-87)
\(\text{CFNACL} = \begin{cases} 1 = \text{CFFFCL} & \text{for the particulate fuel flow regime} & \text{(see Eq. 14.4-76)} \\ 1 = \text{CFFUCL} & \text{for the annular fuel flow regime} & \text{(see Eq. 14.4-74)} \end{cases}\)
\(h_{\text{vg,c1}}\) = convective heat-transfer coefficient between a vapor/gas mixture and cladding which is calculated from a simplified Dittus-Boelter equation in which a Prandtl number of 0.7 is assumed [14-50]:
(14.4‑89)
where
\(\text{Re}_{\text{Mi}} = \frac{D_{\text{Mi}} \cdot \rho_{\text{vg}} \cdot \left| u_{\text{Mi,i}} + u_{\text{Mi,i} + 1} \right|}{2\ VIVG}\)
VIVG = viscosity for the vapor/gas mixture which is input.
\(k_{\text{vg}} = \text{CDVG}\), the input thermal conductivity for a vapor/gas mixture.
(14.4‑89a)
For the calculation of the latter quantity, it is assumed that only the cross-sectional area of the open channel is reduced due to a molten fuel film, but not the perimeter.
14.4.3.4.1.4. No Liquid Sodium Films Present and Sodium Temperature Higher Than Cladding Temperature¶
If \(\theta_{\text{cl,fm}} = 0\), \(T_{\text{Na}} > T_{\text{cl,os}}\), and \(\alpha_{\text{Na}} > \text{CIVOID}\)
(14.4‑90)
i.e., the sodium vapor condensation heat transfer is not decreased with increasing void fraction.
Since the calculation of the heat transfer between sodium and cladding is quite complicated, an overview is given in Table 14.4.1.
14.4.3.4.1.5. Heat Transfer Between Sodium and Structure¶
The calculation of the heat-transfer coefficient between sodium and structure, \(h_{\text{Na,sr}}\), is based on the same equations as indicated in Table 14.4.1. This table should be slightly modified by replacing \(T_{\text{cl,os}}\) by \(T_{\text{sr,os}}\) and by replacing “Na film present on cladding” by “Na film present on structure” in order to make it appropriate as an overview for the sodium-to-structure heat-transfer coefficient.
Heat fluxes per unit of temperature and per unit of generalized smear volume are later needed in the energy equations. They are calculated towards the end of subroutine PLMISC and are simply:
(14.4‑90a)
(14.4‑90b)
14.4.3.4.1.6. Friction Coefficient When No Liquid Sodium Film is Present¶
Friction coefficients for calculating the friction on the sodium/gas mixture have already been given for the situation when much liquid sodium is present in the channels (Eq. 14.4-82) and for the case when liquid sodium films are still present (Eq. 14.4-86a).
When no liquid films are present, Eq. 14.4-86a leads to:
(14.4‑91)
This equation is appropriate for the particulate fuel flow regime. In the annular fuel flow regime, the momentum exchange between the moving fuel film and the sodium/gas mixture is included in the drag term, which describes this momentum exchange. Thus, the friction of the mixture due to the interaction with the stationary cladding or fuel crust has to be reduced from that of the whole channel perimeter.
(14.4‑92)
where the quantities in the parentheses (CFMFCL, CFMFFF and CFFFCL) are explained in Eqs. 14.4-100, 14.4-77, and 14.4-79a.
Void Fraction |
Equation |
\(\alpha_{\text{Na}} < \text{CIVOID}\) |
Eq. (14.4-80) (Single-Phase Correlation) |
\(\text{CIVOID} \leq \alpha_{\text{Na}} \leq \text{CIA4}\) |
If liquid Na film present on cladding (only F.R. = 1): For \(T_{\text{Na}} > T_{\text{cl,os}}\) Eq. (14.4-85) For \(T_{\text{Na}} < T_{\text{cl,os}}\) Eq. (14.4-86) If no liquid Na film left (F.R. = 1 or F.R. = 3): For \(T_{\text{Na}} > T_{\text{cl,os}}\) Eq. (14.4-90) For \(T_{\text{Na}} < T_{\text{cl,os}}\) Eq. (14.4-87) |
\(\text{CIA4} < \alpha_{\text{Na}} < 1\) |
If liquid Na film present on cladding (only F.R. = 1): For \(T_{\text{Na}} > T_{\text{cl,os}}\) Eq. (14.4-85) For \(T_{\text{Na}} < T_{\text{cl,os}}\) Eq. (14.4-86) If no liquid Na film (F.R. = 1 or F.R. = 3): For \(T_{\text{Na}} > T_{\text{cl,os}}\) Eq. (14.4-90) For \(T_{\text{Na}} < T_{\text{cl,os}}\) Eq. (14.4-88) |
\(\alpha_{\text{Na}} = 1\) |
If \(T_{\text{Na}} > T_{\text{cl,os}}\) Eq. (14.4-90) If \(T_{\text{Na}} < T_{\text{cl,os}}\) Eq. (14.4-90) |
14.4.3.4.2. Fuel-to-Coolant Heat Transfer¶
14.4.3.4.2.1. Fuel-to-Coolant Heat Transfer in the Particulate Fuel Flow Regime¶
The heat flow rate per unit of temperature and unit of generalized smear volume is calculated from
(14.4‑93)
where \(f_{\text{fu,N1}}\) is the fraction of fuel which is in contact with liquid sodium which is discussed below. The \({A'}_{\text{Pa}}\) was discussed in Eq. 14.4-69. The above heat-transfer coefficient between fuel and liquid sodium is based on the original Cho-Wright model which considered only the thermal resistance in the fuel [14-9]:
(14.4‑94)
where
\(\text{CIA1}\) is an input constant. A value of 1.0 is recommended based on the L8 and H6 analyses [14-15, 14-12, 14-6]. However, when Eq. 14.4-94 is compared to analytical solutions, a value between 3 and 5 would be appropriate [14-51].
\(r_{\text{Pa}}\) is the radius of the fuel particles or droplets (see input quantities RAFPLA and RAFPSM)
The heat-transfer coefficient between fuel particles and a vapor/gas mixture is calculated from:
(14.4‑95)
where the heat-transfer coefficient \(h_{1}\), which determines the heat transfer between the fuel surface and the vapor/gas mixture is based on Ref. 14-22 and a Prandtl number of 0.7
(14.4‑96)
where
\(\mu_{\text{vg}} = \text{VIVG}\), viscosity of the vapor/gas mixture which is input
\(\rho_{\text{vg}} = \rho_{\text{Nv}} + \frac{{\rho'}_{\text{fi}}}{\theta_{\text{vg}}}\)
The heat-transfer coefficient \(h_{\text{fuvg}}\) considers only 1/10 of the possible heat resistance in the fuel particles. This is because the heat capacity of a vapor/gas mixture is so low that only the outer skin of the particles will be affected by the heat loss of the vapor.
The particle surface area per unit of generalized smear volume is
(14.4‑97)
\({N'}_{\text{Pa}}\) = number of fuel particles in a generalized smear volume (see Eq. 14.4-69)
The contact fraction between fuel and liquid sodium is calculated in the following way:
(14.4‑98)
where
\(\text{CIA2}\) is an input constant. A value of 2.0 is recommended based on the H6 and L8 analysis [14-15, 14-12, 14-6]. A value of 1.0 appears to be too low, because it implies that the liquid sodium appears to be too low, because it implies that the liquid sodium in a partially voided node is heated at the same rate as if the cell were full of sodium. This is because both the effective fuel surface area and the sodium mass (and thus, the sodium heat capacity) are reduced by the same factor in this case.
When the fuel vapor pressure of the moving fuel is above \(10^{-2}\) MPa, fuel vapor condensation on liquid sodium is considered. The heat flow rate per unit of temperature and unit of generalized smear volume is
(14.4‑98a)
where
\(P_{\text{fv}}\) = fuel vapor pressure
\(\text{CFCOFV}\) = fuel vapor condensation coefficient which is input
\(f\) = is a multiplier which is zero when \(\theta_{\text{fm,cl}} = 0\) and 1 when \(\theta_{\text{fm,cl}} > 0\)
\(h_{\text{fu,Nl}}\) and \({A'}_{\text{Pa}}\) are described in Eqs. 14.4-94 and 14.4-97.
This is a rather simple formulation that is at the one extreme limited by the condensation on liquid sodium and at the other extreme by the heat resistance in the fuel droplets.
14.4.3.4.2.2. Fuel-to-Coolant Heat Transfer in the Annular Fuel Flow Regime¶
In this fuel flow regime, the contact area between the fuel and the sodium is significantly reduced from that in the particulate regime. The heat flow rate per unit of temperature and per unit of generalized smear volume is calculated from
(14.4‑99)
where
\({A'}_{\text{fu}}\) is the surface area of the molten fuel film per unit of the generalized smear volume which is calculated from:
(14.4‑99a)
where
(14.4‑100)
i.e., CFMFCL is the fraction of the cladding covered by molten fuel. Regarding CFFUCL, see Eq. 14.4-74; for CFFFCL, see Eq. 14.4-79a.
CFMFFF = fraction of the frozen fuel perimeter covered by molten fuel (see Eq. 14.4-77).
The term \(h_{1}\) in Eq. 14.4-99 is the heat-transfer coefficient between the bulk of the moving fuel film and the surface of the moving film. It is based on the Deissler correlation [14-23, 14-22] and it is very similar to Eq. 14.4-28, except that a different hydraulic diameter and a different Reynolds number are used (see derivation of Eq. 14.4-29).
(14.4‑101)
where
\(\mu_{\text{fu,liq}}\) = liquid fuel viscosity for which the input constant VIFULQ is used
\(C_{\text{p,fu}}\) = liquid fuel specific heat for which the input constant CPFU is used
\(\text{CIA3}\) = input constant (see Eq. 14.2-29)
(14.4‑101a)
where
\(\text{ARMF}\) = cross-sectional area of moving fuel per pin (see Eq. 14.4-71)
\(\text{PECH}\) = channel perimeter associated with one pin (see Eq. 14.4-73)
\(\text{CFFUCL}\) = fraction of the channel perimeter covered by fuel (see Eq. 14.4-74)
(14.4‑102)
The value of the heat-transfer coefficient \(h_{2}\) in Eq. 14.4-99 for sodium void fractions less than the input value CIA4 is
(14.4‑102a)
where
HCFFMI is an input variable which is the convective heat-transfer coefficient between the moving fuel film surface and the sodium droplet/vapor gas mixture
For sodium void fractions larger than CIA4, an interpolation between the above value and a heat-transfer coefficient between the fuel film and a pure vapor/gas mixture is done similarly to the one in Eq. 14.4-88:
For \(\alpha_{\text{Na}} > \text{CIA4}\)
(14.4‑103)
\(\alpha_{\text{Na}}\) = sodium void fraction
CIA4 = input void fraction above which the above interpolation 14.4-103 is done. In the L8 and H6 analyses [14-15, 14-12] a value of 0.5 was used for CIA4, because no other option was available at that time. Using a higher CIA4 should boost the pure vapor/gas temperatures which appeared to be on the low side in the L8 and H6 analyses. A higher value may actually lead to a better agreement with the downward voiding observed in the L8 experiment.
\(h_{\text{vg,fu}}\) = is the heat transfer coefficient between the vapor/gas mixture and the mobile fuel which is based on the same Dittus-Boelter correlation as used for \(h_{\text{vg,cl}}\) (see Eq. 14.4-89).
(14.4‑104)
where
(14.4‑105)
\(\rho_{\text{vg}} = \begin{cases} \rho_{\text{Nv}} + \frac{{\rho'}_{\text{fi}}}{\theta_{\text{vg}}} & \text{for } \alpha_{\text{Na}} < 1 \\ \frac{{\rho'}_{\text{Mi}}}{\left( \theta_{\text{ch,op}} - \theta_{\text{fu}} \right)} & \text{for } \alpha_{\text{Na}} = 1 \\ \end{cases}\)
\(\text{VIVG}\) = viscosity of the vapor/gas mixture which is input
\(D_{\text{Mi}}\) = hydraulic diameter for the mixture flow
Equation 14.4-104 comes from the Dittus-Boelter equation in which a Prandtl number to the power 0.4 appears [14-50]. Since Prandtl numbers for gases are in a narrow range and since the exponent of the Prandtl number further minimizes the dependency of the heat transfer on Prandtl numbers, an average Prandtl number of 0.686 is used to arrive at Eq. 14.4-105.
The fuel vapor to the sodium/gas mixture heat flow rate term per unit of temperature and unit of smear volume is assumed to be limited by the heat resistance in the molten fuel film:
(14.4‑105a)
\(h_{1}, {A'}_{\text{fu}}\) are described in Eqs. 14.4-99 and 14.4-99a
14.4.3.4.2.3. Fuel Crust-to-Sodium/Fission-gas Heat Transfer for the Case of Particulate or Annular Fuel Flow Regime¶
The heat-transfer coefficient between the fuel crust and a two-phase sodium/fission-gas mixture is calculated from
(14.4‑106)
where
\(\text{TKFF}\) is the frozen fuel crust thickness (see Eq. 14.4-76)
For \(\alpha_{\text{Na}} < \text{CIA4},~ h_{1} = \text{HCFFMI}\) (see Eq. 14.4-102)
For \(\alpha_{\text{Na}} > \text{CIA4},~ h_{1}\) is based on an interpolation between HCFFMI and a single-phase gas/vapor heat-transfer coefficient (see also Eq. 14.4-103)
(14.4‑107)
where
(14.4‑108)
where
(14.4‑108a)
\(D_{\text{ch}}\) is hydraulic diameter of the open coolant channel (see Eq. 14.4-58). By dividing it by the term in the brackets, one gets back to the original hydraulic diameter.
\(\text{TKFF}\) is the thickness of the frozen fuel crust (see Eq. 14.4-76)
(14.4‑109)
The latter Reynolds number calculation is very similar to that in Eq. 14.4-105 and several variables are explained there.
The fuel crust-to-sodium/fission-gas heat flow rate per unit temperature and per unit of generalized smear volume is split into a heat transfer to the crust on the cladding and the crust on the structure because temperature are calculated for both crusts.
(14.4‑110)
(14.4‑111)
where
\(\text{CFFFCL}\) is the fraction of the channel perimeter covered by frozen fuel (see Eq. 14.4-79a)
\(\text{CFMFFF}\) is the fraction of CFFFCL covered by moving fuel, which is zero in the particulate fuel flow regime (see Eq. 14.4-77).
14.4.3.4.2.4. Fuel-to-Sodium/Fission-gas Heat Transfer in the Bubbly Fuel Flow Regime¶
The description of this heat-transfer process will require some more investigation. On the one hand, the bubble temperatures should quickly adjust to the surrounding fuel temperature. On the other hand, if liquid sodium is entrapped by the bubbly fuel, the achievement of high temperatures will lead to exaggerated sodium vapor pressures that will rapidly disperse fuel. This may be realistic but the premise that significant amounts at liquid sodium can be entrapped by a bubbly fuel flow is still unclear. Sudden fuel dispersal of denser fuel masses such as observed in the SLSF experiment P2 [14-52] or in the TREAT tests L3 and L4 [14-53, 14-54] may have been due to non-prototypical lateral injections of liquid sodium into the molten fuel masses. (However, such lateral injections of liquid sodium may be prototypical in the transition phase.) The current heat-transfer calculation in PLUTO2 is relatively straightforward and can be limited via an input parameter.
For the calculation of the heat transfer between fuel and the sodium/fission-gas mixture in the bubbly fuel flow regime, an estimate of the bubble radius is needed. For the maximum bubble radius, it is assumed that
This implies that a string of spherical bubbles is assumed for larger void fractions, rather than one or a few elongated bubbles. For decreasing void fractions, the bubble radius is assumed to be:
(14.4‑112)
where
\(\text{CIBBIN}\) is the input void fraction above which a bubbly fuel regime can be initiated.
When \(\alpha_{\text{bb}}\) goes to zero, \(r_{\text{bb}}\) goes to \(r_{\text{bb,mx}} \cdot 0.05\). This is the assumed minimum bubble radius. For the heat-transfer coefficient between bubbly fuel and the two-phase mixture, it is assumed that
(14.4‑113)
where
HCFUBB is an input heat-transfer coefficient describing the heat transfer between the bulk of the fuel and the bubble surfaces. It is also used to control the heat transfer between fuel vapor and the mixture (see Eq. 14.4-166a).
and
(14.4‑114)
where
CDNL, CDVG are input conductivities for liquid sodium and the vapor/fission-gas mixture, respectively.
The heat flow rate per unit of temperature and unit of generalized smear volume is:
(14.4‑115)
where
(14.4‑116)
which is the total bubble surface area in a unit of smear volume. \(\left( \theta_{\text{ch,op}} - \theta_{\text{fu}} \right)\) is the total bubble volume in a unit of generalized smear volume.
The heat flow rate term between fuel vapor and the bubbles is assumed to be controlled by the input heat-transfer coefficient HCFUBB
(14.4‑116a)
14.4.3.4.3. Moving Fuel-to-Cladding, Moving Fuel-to-Structure, and Moving Fuel-to-Fuel-crust Heat Transfer¶
In the particulate fuel flow regime, no heat transfer between moving fuel and cladding, structure, or fuel crust is considered. However, fuel-vapor condensation on cladding and structure is considered when there is no liquid sodium film left on the cladding or structure. The heat flow rates per unit of temperature and per unit of generalized smear volume are
(14.4‑117)
(14.4‑117a)
where
\(\text{CFNACL} = 1 - \text{CFFFCL}\) (see Eq. 14.4-77)
\(\text{CFCPOFV}\) = fuel vapor condensation coefficient, which is input.
In the annular and bubbly fuel flow regimes, very similar expressions are used for the heat flow rate terms. The difference lies in the different values for the contact coefficients and the Reynolds numbers that are used.
The heat-transfer coefficient for the moving fuel-to-cladding and moving fuel-to-structure coefficient is the same and it is also used for the calculation of the moving fuel-to-fuel-crust heat transfer. It is based on the Deissler correlation [14-23, 14-22] which was already discussed earlier (see Eq. 14.4-28). However, a conduction term was added to this correlation because it is not designed for very slow or stagnant flow conditions. For the partial or fully annular fuel flow, the following relationship holds:
(14.4‑118)
where
TKFU is the thickness of the moving fuel film (see eq. 14.4-75). In the above equation, this film thickness is not allowed to become smaller than 1/10 of the channel hydraulic diameter. Thus, the additional term will not dominate the equation except for very slow or stagnant flow conditions.
CIA3, VIFULQ, CPFU are all input constants, which were explained in Eq. 14.4-28.
\(D_{\text{fu}}\) is the hydraulic diameter of moving fuel film (see Eq. 14.4-101).
(14.4‑119)
In the bubbly fuel flow regime, pretty much the same form of the heat-transfer coefficient is used. However, some of the terms are evaluated differently:
\(D_{\text{fu}} = D_{\text{ch}}\)
\(\text{TKFU} = \frac{D_{\text{ch}}}{4}\)
where \(D_{\text{cg}}\) is the open channel hydraulic diameter, which takes the frozen crusts into account (see Eqs. 14.4-58 and 14.4-68).
If the energy of the moving fuel film is below the solidus energy, which is possible if solid fuel gets released from an underlying melting cladding, only the pure conduction part of Eq. 14.4-118 will be used. The thickness TKFU is, in this case, always calculated from Eq. 14.4-75 and no lower limit is assumed for it as in Eq. 14.4-118. The calculation of this special heat-transfer coefficient and of the related heat flow rates are performed near the end of PLMISC, whereas the regular coefficients and flow rates are done in the middle section of PLMISC.
The heat flow rates per unit temperature and per unit of generalized smear volume are
(14.4‑120)
and
(14.4‑121)
where
(14.4‑122)
CFMFCL is the fraction of the channel perimeter covered with moving fuel (see Eqs. 14.4-74 and 14.4-77). In the case of the bubbly fuel flow regime.
(14.4‑123)
because all the structure or cladding which is not covered by frozen fuel is assumed to be in contact with moving fuel in this case.
For the fuel vapor condensation on cladding and structure, heat flow rate terms per unit temperature and per unit smear volume are used which are similar to Eqs. 14.4-117 and 14.4-117a:
(14.4‑124)
(14.4‑124a)
where
\(\text{CFNACL} = 1 - \text{CFFUCL}\) (see Eq. 14.4-74)
The heat-transfer coefficient between moving fuel and a frozen fuel crust is calculated form
(14.4‑125)
where
TKFF = the thickness of the frozen fuel crust (see Eqs. 14.4-76 and 14.4-79).
\(k_{\text{fu}} = \text{CDFU}\) which is the input fuel conductivity
The heat flow rates per unit temperature and per unit of smear volume for the annular flow regimes are
(14.4‑126)
(14.4‑127)
where
In the bubbly fuel flow regime
(14.4‑128)
(14.4‑129)
All the frozen fuel is assumed to be covered with moving fuel in the bubbly flow regime. Therefore, CFMFFF is 1.0 in this case.
The multiplication with the A’s in the above equations is not done in subroutine PLMISC, but in PLTECS which is called next in the calling sequence.
14.4.3.5. Partial Momentum exchange Terms Between Annular Fuel and the Sodium/Fission-gas Mixture¶
The friction coefficient CFFRMF for the calculation of the drag between a moving fuel film and the sodium/gas mixture is calculated from
(14.4‑130)
where
\(\text{AFRV, BFRV}\) = input constants
(14.4‑131)
\(\text{CFMFCL} = \text{CFFUCL} - \text{CFFFCL}\)
\(\text{CFFUCL}\): see Eq. 14.4-74
\(\text{CFFFCL}\): see Eq. 14.4-79a
\(\text{CFMFFF}\): see Eq. 14.4-77
In subroutine PLMISC, a contact coefficient that gives the fraction of the cladding and fuel crust in contact with the moving fuel is also set. It is needed in PLMOCO for the calculation of the fuel friction term. In the annular fuel flow regime, it is:
(14.4‑132)
The terms on the right-hand side of this equation were also used in Eq. 14.4-130.
If the bubbly fuel flow regime holds:
(14.4‑133)
14.4.4. Mobile Fuel and Fuel Crust Energy Equations¶
14.4.4.1. Mobile Fuel Energy Equation¶
The mobile fuel energy equation, which is solved at the end of subroutine PLMISC, includes only source and sink terms due to heat transfer. The energy changes due to fuel plateout and the energy changes due to the addition of released or remelting fuel crusts are taken into account in subroutine PLFREZ which was discussed in Section 14.4.3.2. The energy change due to the addition of fuel ejected from the pins is taken into account in subroutine PL1PIN.
The mobile fuel energy equation in differential form reads:
(14.4‑134)
where
\(A_{\text{fu}}, A_{\text{vg}}\) = cross sectional areas of the mobile liquid or solid fuel and of the vapor/gas mixture, respectively
\(A_{\text{fu,k}}^{l}\) = interaction area between moving fuel and component \(k\) per unit length
\(A_{\text{fv},l}^{l}\) = interaction areas between fuel vapor and component \(l\) per unit length
\(\rho_{\text{fv}}\) = saturated fuel vapor density
\(\rho_{\text{fu}}\) = theoretical density of liquid or solid fuel
\(e_{\text{fu}}\) = internal energy of liquid or solid fuel
(14.4‑135)
\(\lambda_{\text{fv}}\) = fuel heat of vaporization
\(Q\) = fission heat source per kg of fuel that is calculated from Eq. 14.4-25.
However, \(F_{\text{POWER}}\) is always 1 in this case.
By inserting Eq. 14.4-135 into the first term of Eq. 14.4-134, one obtains:
(14.4‑136)
By inserting Eq. 14.4-136 into 14.4-134 and dividing the resulting equation by AXMS, and by also using the definitions of the generalized smear densities, one arrives at:
(14.4‑137)
where
\({\rho'}_{\text{fuch}} = {\rho'}_{\text{fu}} = {\rho'}_{\text{fv}}\)
\({\rho'}_{\text{fu}}\) = generalized smear density of the moving liquid or solid fuel
\({\rho'}_{\text{fv}}\) = generalized smear density of fuel vapor
\({A'}_{\text{fu,k}}\) = interaction area between moving liquid or solid fuel and component \(k\) in a unit of generalized smear volume
\({A'}_{\text{fv},l}\) = interaction area between fuel vapor and component \(l\) in a unit of generalized smear volume
The different heat flow rates which are summed up in Eq. 14.4-137 can be written as:
\(H_{\text{fu,na}} \cdot \left( T_{\text{fu}} - T_{\text{Ta}} \right)\): see Eq. 14.4-93 for particulate fuel flow and Eq. 14.4-99 for annular flow and Eq. 14.4-115 for bubbly flow
\(H_{\text{fu,cl}} \cdot \left( T_{\text{fu}} - T_{\text{cl,os}} \right)\): see Eqs. 14.4-120 and 14.4-122. For particulate flow this term is zero.
\(H_{\text{fu,sr}} \cdot \left( T_{\text{fu}} - T_{\text{sr,os}} \right)\): see Eqs. 14.4-121 and 14.4-122. For particulate flow this term is also zero.
\(H_{\text{fu,ffcl}} \cdot \left( T_{\text{fu}} - T_{\text{ffcl}} \right)\): see Eqs. 14.4-126, 14.4-128
\(H_{\text{fu,ffsr}} \cdot \left( T_{\text{fu}} - T_{\text{ffsr}} \right)\): see Eqs. 14.4-127, 14.4-129
\(H_{\text{fv,N1}} \cdot \left( T_{\text{fu}} - T_{\text{Na}} \right)\): see Eqs. 14.4-98a, 14.4-105a, and 14.4-116a
\(H_{\text{fv,cl}} \cdot \left( T_{\text{fu}} - T_{\text{cl,os}} \right)\): see Eqs. 14.4-177 and 14.4-125; in the bubbly flow regime this term is zero
\(H_{\text{fv,sr}} \cdot \left( T_{\text{fu}} - T_{\text{sr,os}} \right)\): see Eqs. 14.4-117a and 14.4-124a; in the bubbly flow regime this term is zero
where \(H\) is heat transfer coefficient times heat transfer area.
The main part of the energy equation for the moving fuel is solved at the end of subroutine PLMISC. However, heat-transfer terms between moving fuel and the frozen crust on cladding and structure are only included in subroutine PLTECS which is called after PLMISC.
Since the moving fuel energy equation is solved explicitly (i.e., using only beginning-of-time step values in the convective terms and in the heat-transfer terms), it is possible to solve this equation for the fuel energy rather than for fuel temperature. This has the advantage that the heat of fusion can be easily taken into account. The moving fuel energy is stored in a permanent array in PLUTO2, and fuel temperatures, which are needed in the heat-transfer terms and for calculating fuel vapor pressure, are obtained from function subroutine TEFUEG. The equations solved in this subroutine are the following:
If \(e_{\text{fu}} < e_{\text{fu},\text{sol}}\)
(14.4‑138)
(14.4‑139)
If \(e_{\text{fu,sol}} < e_{\text{fu}} < e_{\text{fu,liq}}\)
(14.4‑140)
(14.4‑141)
If \(e_{\text{fu,liq}} < e_{\text{fu}}\)
(14.4‑142)
(14.4‑143)
The function subroutine TEFUEG is called in subroutine PLSET2, which is called whenever control is transferred to PLUTO2 and which sets all temporary arrays such as the fuel temperature. Moreover, it is called for all nodes containing fuel at the end of subroutine PLTECS after nearly all the updating of the moving fuel energy has been done. In nodes receiving fuel that is ejected from the pins, the fuel energy is further updated and function subroutine TEFUEG is used again for further updating the fuel temperatures in such nodes.
For the numerical solution of Eq. 14.4-137, the main storage term is rewritten:
(14.4‑144)
In finite difference form, the above equation is written as
(14.4‑144a)
which can be arrived at by writing
The derivative of the generalized smear density in Eq. 14.4-144a is
(14.4‑145)
which is the fuel mass conservation equation without source or sink terms. Since the energy Eq. 14.4-137 does not include loss or gain terms due to mass sinks or sources (these are separately included in the fuel freezing and crust release calculations in subroutine PLFREZ and in the fuel ejection calculation in subroutine PLIPIN), the density changes in Eq. 14.4-137 are solely due to mass convection. By writing Eq. 14.4-137 in finite difference form and by including Eq. 14.4-144a and Eq. 14.4-145, one arrives at
(14.4‑146)
In the second term of the left-hand side, it was assumed that the heat of vaporization is constant over the range considered (3700-5000 K). The temperature change in the second term on the left-hand side of Eq. 14.4-146 can be related to the liquid energy change by
(14.4‑146a)
By using Eq. 14.4-146a in Eq. 14.4-146, the left-hand side of this equation can be rewritten:
(14.4‑147)
The convective terms are evaluated by using full donor cell differencing. The first two terms on the right-hand side are actually the convective fluxes of the fuel mass conservation equation (see Eq. 14.4-34) multiplied by \(e_{\text{fu}}\) (note that in Eq. 14.4-34, \({\rho'}_{\text{fu}}\) is written as \({\rho'}_{\text{fuch}} - {\rho'}_{\text{fv}}\)). These convective mass fluxes are used in the energy equation to evaluate the first two terms on the right-hand side of Eq. 14.4-146. The convective energy flux of the solid or liquid fuel is evaluated in the following way (see the schematic below Eq. 14.4-130).
(14.4‑148)
The first term on the right-hand side is evaluated in the following way:
(14.4‑149)
The second term on the right-hand side is evaluated correspondingly. The FORTRAN name for the convective energy fluxes is \(\text{COFUOS} \left( I \right)\). They are calculated in the subroutine solving the mass conservation equations, PLMACO. Equation 14.4-146 is solved for \(\Delta e_{\text{fu}}\) at the end of subroutine PLMISC. As mentioned earlier, the heat flow terms between fuel and the frozen crust on the cladding and on the structure are only later included in subroutine PLTECS, which is called after PLMISC. After these additional updates to the energy equations have been made, the fuel temperature is calculated by using function subroutine TEFUEG (see Eqs. 14.4-138-14.4-143).
14.4.4.2. Fuel Crust Energy Equations¶
The energy equations for the stationary fuel crusts on the cladding and structure are solved in subroutine PLTECS (PLUTO2 TEMPERATURE CALCULATION OF CLADDING AND STRUCTURE). The calculation of the fuel crust temperatures is done at the beginning of this routine and provides heat flow rates per unit temperature and unit smear volume for the cladding and structure calculation which make up the bulk of this routine and are described in Section 14.5.
Only the temperatures of the fuel crusts on cladding and structure (one for each crust) are stored in permanent arrays in PLUTO2. The beginning of time-step energy of the fuel crust on cladding is determined form the beginning of time-step temperature by
(14.4‑150)
where
\(C_{\text{p,fu}} = \text{CPFU}\) which is the input value of the fuel specific heat.
EGFUTE is a function subroutine to convert form temperatures to energies. It is could be used over the entire temperature range of the fuel, but by calling it only for the rare case when the crust is above the solidus temperature, computer time is save.
The change in the internal energy of the cladding fuel crust per PLUTO2 time step is calculated from:
(14.4‑151)
where
\(f_{\text{ffcl}} = \frac{{A'}_{\text{c1}}}{{A'}_{\text{c1}} + {A'}_{\text{sr}}}\) is the fraction of all the fuel crust which is on the cladding
\(H_{\text{ff,Na}}\) has been described in Eq. 14.4-110.
\(H_{\text{ff,fu}}\) has been described in Eq. 14.4-111.
(14.4‑151a)
where
\(\text{TKFF}\) is the thickness of the frozen fuel crust
\(\text{CFFFCL}\) is the fraction of the cladding perimeter covered by fuel crust (see Eq. 14.4-76)
After the new internal energy has been calculated from
(14.4‑152)
the new temperature is calculated from
(14.4‑153)
The function subroutine TEFUEG for converting from fuel energies to temperatures is only called for the rate case when the crust energy is above the solidus energy in order to save computer running time.
The calculation of the structure crust temperature, \(T_{\text{ffsr}}\), is done correspondingly. In this case, the fraction of the crust that is on the structure is assumed to be:
(14.4‑154)
14.4.5. Sodium/Fission-gas Energy Equation and Channel Pressure Calculation¶
The subroutine PLNAEN (PLUTO NA ENERGY) which calculates the sodium temperature change for the two-phase sodium/fission-gas mixture and the single phase sodium/vapor/fission-gas mixture is nearly the same as the LEVITATE sodium energy equation (see Section 16.4.3.5) and therefore is not described in detail here. Only the slight differences between the two routines will be discussed.
One difference is due to the fact that LEVITATE treats more components than PLUTO2. These additional components are the moving molten steel films (designated by subscripts se) and the moving fuel and steel chunks (designated by subscript f1 and s1, respectively). Because of the presence of these components, three additional heat-transfer terms appear in the LEVITATE sodium energy subroutine LENAEN.
Another difference between the two sodium energy equations is due to the fact that PLUTO2 treats liquid sodium films on the cladding. This has not yet been incorporated in LEVITATE. In PLUTO2, the convective energy fluxes for the two-phase sodium/gas mixture use sodium densities and sodium qualities which exclude the liquid sodium film. The quality of the moving two-phase mixture in PLUTO2 is
(14.4‑155)
In LEVITATE, the sodium quality \(x_{\text{Na}}\) is also based on the above equation, but with \({\rho'}_{\text{Na,fm}} = 0\) in all nodes. It should be noted here that the liquid film treatment in PLUTO2 does not come into the energy equation in other ways because the liquid sodium film is considered to be in thermal equilibrium with the moving sodium in a node.
Subroutine PLNAEN includes most of the PLUTO2 channel pressure calculation. However, an updating is done later in subroutine PL1PIN for cells into which fuel and/or gas is injected. Subroutine PLNAEN includes the calculation of fission-gas pressure, sodium saturation pressure or superheated sodium vapor pressure, fuel vapor pressure, and, if necessary, single-liquid-phase pressure of sodium. LEVITATE does not treat the latter because it is not important for voided channel conditions. LEVITATE has a much more refined fuel vapor pressure calculation than PLUTO2, tub this is not performed in the LEVITATE sodium energy equation LENAEN. Moreover, LEVITATE treats steel vapor pressure. But this is also not calculated in LENAEN.
In single-phase liquid sodium pressures do not play a significant role, PLUTO2 will add up the partial pressures according to Dalton’s law:
(14.4‑156)
In the above equation, the fission-gas pressure contribution is based on the ideal-gas equation (see Eqs. 14.4-157 and 14.4-158). The fission gas is assumed to be always in thermal equilibrium with the two-phase sodium mixture. Therefore, no separate fission-gas temperature appears in the equation-of-state. For sodium void fractions greater than 70%, the fission-gas pressure is calculated from the ideal-gas equation:
(14.4‑157)
where
\(R_{\text{fi}}\) = RGAS gas constant for fission gas which is the universal gas constant divided by the averaged molecular weight of xenon, krypton, and helium (the latter is only important for near-fresh fuel)
\(\theta_{\text{vg,un}}\) is the generalized volume fraction of the vapor gas space when the compressibility of liquid sodium is not taken into account.
For sodium void fractions of less than 70%, the fission-gas pressure calculation takes the sodium compressibility into account. This is done by solving the ideal-gas equation which includes the sodium compressibility:
The positive solution of this quadratic equation is
(14.4‑158)
where
\(K_{\text{N1}} = \text{CMNL}\), the adiabatic liquid sodium compressibility
\(\theta_{\text{N1}}\) = generalized volume fraction of liquid sodium
This equation will default to a pure liquid phase equation if the fission-gas density is zero and the \(\theta_{\text{vg,un}}\) is negative.
When the latter is true, i.e. when the liquid sodium does not fit into the numerical node without compressing it, the fission-gas pressure, which is calculated from Eq. 14.4-158, is compared with the sum of the saturation pressures:
(14.4‑159)
(14.4‑159a)
where \(P_{\text{fi}}\) is calculated from Eq. 14.4-158.
In the pure vapor/gas regime in which no liquid sodium is left (i.e., sodium quality equals one) the channel is calculated from
where
(14.4‑159b)
The “gas constant” RGNA is not really a constant but is based on an interpolation between a special “gas constant”, which leads to the sodium saturation pressure when inserted into Eq. 14.4-159b, and the actual general gas constant divided by the molecular weight of sodium vapor. This is described in more detail in Section 16.4.3.5 in the LEVITATE description.
14.4.6. Momentum Equations in the Coolant Channel¶
14.4.6.1. Differential Equations for the Sodium/Vapor/Gas/Mixture and for the Moving Solid or Liquid Fuel¶
14.4.6.1.1. Momentum Equation for the Sodium/Vapor/Gas Mixture¶
The momentum equation for the mixture of liquid sodium, sodium vapor, fission gas, and fuel vapor is presented in terms of the generalized smear densities, volume fractions and sources and sinks. The step from the more basic equation, which includes the cross sectional areas of each component, to Eq. 14.4-169 below has been omitted because a similar step has been explained earlier for the mass and energy equations; see Eqs. 14.4-15 or 14.4-134. However, it should be remembered that the following equation is written for variable cross section flow. The variable cross section is included in the generalized smear densities and volume fractions.
(14.4‑160)
where the last three terms are sink terms due to sodium droplet de-entertainment onto the liquid sodium film, and sodium vapor and fuel vapor condensation on clad and structure. Source terms due to fuel evaporation and dissolved fission gas release are disregarded. All other terms will be explained only after the above equation has been modified by inserting the following mass conservation for the moving sodium/vapor/gas mixture:
(14.4‑161)
where the source and sink terms on the right-hand side are due to free fission-gas equation, sodium film entrainment, sodium droplet de-entrainment onto the liquid film and sodium vapor condensation on cladding and structure. Source terms due to sodium evaporation, fuel evaporation and dissolved fission-gas release are not considered.
Equation 14.4-161 can be inserted into Eq. 14.4-160 if the first term in Eq. 14.4-160 is split. Splitting this term and inserting the mixture mass conservation equation leads to a momentum equation in which the velocity is the dependent variable and not the mass flux. It can be seen later that this is of key importance for the simultaneous solution of the two momentum equations considered. (If mass and momentum equations for both fluids are solved simultaneously as in SIMMER-II [14-19], this splitting of the mass flux will not be necessary).
Splitting the first term in Eq. 14.4-160 and inserting Eq. 14.4-161 leads to
(14.4‑162)
where
\(f_{\text{bb}}\) = is a factor which is zero of the particulate and annular flow regime and has a value of one for the bubbly flow regime. This means that the apparent mass effect is considered only for the bubbly flow regime. This was done because in this latter flow regime accelerating or decelerating low-density bubbles also have to accelerate or decelerate high-density fuel of half the bubble volume (apparent mass effect). This has a significant effect on the slip between the bubbles and the continuous fuel [14-49].
\({S'}_{\text{Na,et}}\) = the mass of sodium entrained per unit time and per unit of smear volume
\({S'}_{\text{fi,ej}}\) = the mass of free fission gas being ejected into the channel per unit of time and unit of smear volume
\(F_{\text{Mi}}\) = the modified friction coefficient which is different for each flow regime:
\(F_{\text{Mi,FR3}}\) = see Eq. 14.4-92
\(F_{\text{Mi,FR4}} = 0\) because there is no contact between the sodium/gas mixture and the clad or structure in the bubbly flow regime.
\(F_{\text{drag}}\) = a part of the drag force which is strongly dependent on the flow regime. For the particulate flow regime this factor is [14-49, 14-63]:
(14.4‑163)
where
\({N'}_{\text{Pa}} = \frac{\theta_{\text{fu}}}{\frac{4}{3} \pi r_{\text{Pa}}^{3}}\), which is the number of fuel particles in a unit of generalized smear volume
CIA5 is an input controlling the drag dependence on the void fraction. A value of \(-1.7\) is recommended based on references [14-49] and [14-63].
(14.4‑164)
where
(14.4‑165)
\(\mu_{\text{Mi}}\) = viscosity of the sodium/gas mixture (see Eq. 14.4-83a)
The partial drag term for the annular fuel flow regime is:
(14.4‑166)
where
CFFRMF includes the Reynolds number dependency of the drag and the fraction of the perimeter covered by moving fuel (see Eq. 14.4-130)
\(D_{\text{Mi}} = D_{\text{ch}} \cdot \frac{\theta_{\text{Mi}}}{\theta_{\text{ch,op}}}\), where the \(D_{\text{ch}}\) accounts for the frozen crust. The multiplication with the ratio of volume fractions accounts for the flow cross section reduction of the mixture due to moving fuel and sodium films. The wetted perimeter is assumed to stay unchanged. This is a reasonable assumption for a true subchannel geometry.
The partial drag term for the bubbly flow is similar to that for the particulate flow (see Eq. 14.4-163) because non-deformable bubbles are assumed in PLUTO2.
(14.4‑167)
where
\(r_{\text{bb}}\) = bubble radius which cancels out when the drag coefficient (see Eq. 14.4-170) is later inserted.
\(C_{\text{drag}}\) = see discussion below and Eq. 14.4-170
Transient drag coefficients for bubbly flow are not available. Therefore a drag coefficient is used which is based on steady-state experiments. The calculation of a terminal (for steady-state) velocity can be determined by balancing the gravitational and drag forces.
(14.4‑168)
A terminal rise velocity obtained from the drift velocity of the bubbles for the churn turbulent regime similar to that suggested by Zuber [14-19] is used:
(14.4‑169)
In the formulation of Zuber, this is a drift velocity. For the relatively high fuel fraction assumed in the bubbly fuel flow regime in PLUTO2, the actual bubble velocity and drift velocity are not very different.
After introducing Eq. 14.4-169 into Eq. 14.4-168 one obtains:
(14.4‑170)
where
\(C_{\text{x}}\) = 1.1392 based on the above Eqs. 14.4-168 and 14.4-169. The input value of CIA6 is \(C_{\text{x}} \cdot 3/8\) which equals 0.4272.
The great advantage of Eq. 14.4-170 is that the bubble radius, which is difficult to evaluate, appears in the numerator and therefore cancels in the drag term described in Eq. 14.4-167. However, it is somewhat questionable whether the bubbly flow in PLUTO2 is really in a churn turbulent regime. At any rate, the above formulation gives a rather high draft force, which is appropriate for a bubbly flow regime.
14.4.6.1.2. Momentum Equation for the Moving Liquid or Solid Fuel¶
The differential equation for the fuel momentum conservation is presented in a modified form in which the fuel mass conservation is already included. The latter applies only to the liquid or solid fuel (compare with Eq. 14.4-16)
(14.4‑171)
A sink term due to fuel freezing and a source term due to frozen fuel crust release or remelting are not included in this mass conservation and in the momentum conservation because they are calculated separately in the subroutine treating the fuel plateout and crust release (PLFREZ).
By splitting the momentum storage term and by including Eq. 14.4-171 (this is similar to the derivation of Eq. 14.4-162), one arrives at:
(14.4‑172)
where
drag and apparent mass forces are the same as in the mixture momentum Eq. 14.4-162 except that they act in the opposite direction,
\({S'}_{\text{fu,ej}}\) is the mass of fuel ejected from the failed pins per unit time per unit of generalized smear volume,
and
CIFUMO is an input value between 0 and 1. It determines how much of the axial momentum of the fuel just behind the cladding rupture is retained when the fuel is ejected into the channel. In the L8 analysis [14-15, 14-12] a value of 1 was used. But it appears that for midplane failures, which are not rapidly expanding axially, a lower value may be more appropriate,
\(F_{\text{fu}}\) is a part of the fuel friction force between moving fuel and cladding, structure, and frozen fuel and is dependent on the fuel flow regime,
\(F_{\text{fu,FR1}} = 0\) because no friction loss between fuel particles or droplets and the walls is assumed. This is based on observations form TREAT and CAMEL out-of-pile experiments in which the particulate fuel easily travels long distances.
(14.4‑173)
\(\text{Re}_{\text{fu}} = \frac{\rho_{\text{fu}} \cdot \left| u_{\text{fu}} \right| \cdot D_{\text{fu}}}{\mu_{\text{fu}}}\)
\(\mu_{\text{fu}} = \text{VIFULQ}\) is input viscosity of liquid fuel
\(D_{\text{fu}} = \frac{\theta_{\text{fu}} \cdot D_{\text{ch}}}{\theta_{\text{ch,op}} \cdot \text{CTFRFU}}\)
CTFRFU is the fraction of open channel perimeter covered by moving fuel (this includes fuel moving over crusts; see Section 14.4.3.5).
CIFRFU and CIREFU are both input parameters which should be set in a manner such that there is not a sudden jump in the friction force at \(\text{Re}_{\text{fu}} = \text{CIREFU}\)
14.4.6.2. Finite Difference Equations, Simultaneous Solution Approach, and Subroutine PLMOCO¶
One of the problems of using a staggered grid is that the solution of the momentum equation on the cell edges requires many variables that are defined on the cell centers. In PLUTO2, most of the needed quantities are obtained by using half the sum of the upstream and downstream quantities. Therefore, neighboring cells should have a similar length in PLUTO2, although a length ratio of less than 2 to 1 for neighboring cells is not considered to cause significant inaccuracies. In the code, all variables that are obtained by halving the sum of the upstream and downstream values contain the two-letter sequence BD (for boundary) at the end of the variable name. In the finite difference equations, no special labeling of these variables will be made.
The finite difference forms of the momentum equations are not in conservative form, although both the mass and energy equations are in conservative form. This was prompted by the experience that the calculations were not always stable (in particular for stagnation cells) when using conservative momentum equations. The latter can be easily obtained by not combining the first two terms on the right-hand side of eq. 14.4-162 and by integrating the equation from the cell midpoint below a cell boundary to the cell midpoint above it (i.e., over a “momentum cell”).
In the approach in PLUTO2, the first two terms on the right-hand side of eq. 14.4-162 are combined:
(14.4‑174)
All terms in Eq. 14.4-162 that include a product of velocities are finite differences in the following manner:
(14.4‑175)
(14.4‑176)
(14.4‑177)
where \(\Delta\) implies change over a time step at a given mesh point and \(\delta\) implies change over a mesh interval at a given time.
By inserting Eqs. 14.4-174 through 14.4-177 into Eq. 14.4-162, by switching from partial derivatives to \(\delta\)’s and \(\Delta\)’s, and by collecting all terms which include \(\Delta u_{\text{Mi}}\) on the left-hand side yields:
(14.4‑178)
The superscripts \(n\), that denote the beginning of the time step, have been dropped in this equation. Before elaborating on the spatial differencing, the elimination of the \(\Delta u_{\text{fu}}\)’s on the right-hand side of this equation will be described. This is achieved by inserting the finite difference form of the fuel momentum equation into the above equation. The finite difference form of the fuel momentum equation can be obtained by performing the same manipulations which were done to arrive at Eq. 14.4-178. The fuel momentum Eq. 14.4-172 reads in finite difference form:
(14.4‑179)
where the second term in the bracket is solely due to the apparent mass (or inertial) force and
(14.4‑180)
(14.4‑181)
Equation 14.4-179 can now be inserted into Eq. 14.4-178 in order to eliminate the \(\Delta u_{\text{fu}}\)’s from Eq. 14.4-178. This is necessary to order to perform the simultaneous solution of the mixture and fuel momentum equations. Without this simultaneous solution of the momentum equations, the solution of this two-fluid problem is not stable. The main reason is that the drag terms in the two momentum equations, which act in opposite directions and can be quite large, would not always have the same absolute value, if not solved simultaneously. These discrepancies between the absolute values of the drag would cause serious instabilities.
By inserting Eq. 14.4-179 into Eq. 14.4-178 and collecting all the terms with \(\Delta u_{\text{Mi}}\) on the left-hand side, one obtains:
(14.4‑182)
where
(14.4‑183)
(14.4‑184)
AMIIN and BMIIN includes most of the terms related to the apparent mass force (the others are included in AHELP and BHELP).
Equation 14.4-182 can be solved for \(\Delta u_{\text{Mi}}\). This \(\Delta u_{\text{Mi}}\) is then used in the fuel momentum Eq. 14.4-179 to solve for the fuel velocity increment \(\Delta u_{\text{fu}}\). As discussed earlier, this simultaneous solution of the two momentum equations is of key importance for achieving a stable solution of the two-fluid problem.
An item not yet discussed is the finite differencing of the spatial derivatives. As mentioned earlier, an important feature in PLUTO2 is that the convective momentum and mass fluxes are combined (see Eq. 14.4-174) which makes the momentum equations nonconservative but leads to stable solutions. The spatial differencing of the convective term is demonstrated for the mixture momentum flux term
(14.4‑185)
The finite differencing of the fuel momentum flux term is done similarly.
The mixture momentum fluxes for the lowermost and for the uppermost cells use the velocities of the sodium slug interfaces if upstream or downstream velocities are needed in the above convective flux calculation. For these nodes, the \(\Delta z_{\text{i}}\)’s are the distances between the slug interfaces and the lowermost or uppermost cell boundaries at which the mixture momentum equation is solved.
The fuel velocities at the extremes of the fuel region are needed for the calculation of the convective fuel momentum fluxes at the lowermost and uppermost cell boundaries and also for the calculation of the interface locations of the fuel domain which is done in subroutine PLIF. If the fuel in the uppermost or lowermost fuel node is in a continuous fuel flow regime, the velocity of the upper or lower fuel interface will be set to the velocity of the nearest cell boundary for which the fuel velocity has been calculated by the fuel momentum equations. If the uppermost or lowermost fuel node is in a particulate flow regime, a Lagrangian momentum equation will be solved for a fuel particle at the upper or lower end of the fuel region. The force terms in this momentum equation are equivalent to those in the regular Eulerian momentum equation (see Eq. 14.4-172), but there is, of course, no convective flux terms in this Lagrangian momentum equation.
Also needed is a spatial differencing of the gradients of the relative velocities between mixture and fuel which appear in Eqs. 14.4-183 and 14.4-184. The following upwind differencing which is keyed on the much more sensitive mixture velocity is done in the following way:
(14.4‑186)
Subroutine PLMOCO (PLUTO2 MOMENTUM CONSERVATION) sets up all of the coefficients needed for the solution of the momentum conservation. (This is mainly because these coefficients are needed at the cell edges and have previously been set only at the midpoints. However, most interfacial drag terms were not set up earlier.) Subroutine PLMOCO also sets up the convective momentum flux terms and it performs the simultaneous solution fo the two momentum equations. Moreover, the calculation of the fuel region interface velocities, which was described in the previous paragraph, is done. Subroutine PLMOCO also calculates the velocity changes of the liquid sodium slugs above and below the interaction region. This is described in the next section.
14.4.6.3. Velocity Calculation for the Liquid Sodium Slug Interfaces¶
Ideally, the liquid sodium slugs should be modeled with a fully compressible treatment. Although this was done in the original PLUTO code [14-3. 14-4], it has not been incorporated in PLUTO2 because it is not considered important for whole-core calculations and because a fully compressible calculation in the liquid slugs requires the use of very small time steps. In an earlier stand-alone version of PLUTO2, an optional compressible treatment, which allows a separate time step in the liquid slugs and in the interaction region, should eventually be incorporated into SAS4A/PLUTO2 for use in expensive analyses.
In the currently available treatment in SAS4A/PLUTO2, an acoustic approach is used in the lower and upper slug until the initial pressure waves reach the subassembly inlet and exit, respectively. From then on, the liquid sodium slugs are treated with an incompressible approach.
The initial acoustic approach in PLUTO2 is only used until the pressure wave hits the nearest free surface and not during the round trip time of the expanding and receding pressure wave. The latter is commonly used for the acoustic approximation, but was not used in PLUTO2 because comparisons with the fully compressible PLUTO cod [14.3, 14-4] showed better agreement when only the time for reaching the nearest free surface was used. This time is evaluated in PLUTO2 based on the velocity of sound. The velocity of sound in the lower slug for temperature-independent density and compressibility is:
(14.4‑187)
where
\(\rho_{\text{N1,ls}}\) is the average density of the lower sodium slug at the time of PLUTO2 initialization
\(K_{\text{N1}}\) is the liquid sodium compressibility which is an input constant (see CMNL)
The time to reach the free surfaces at the inlet or outlet are calculated from:
(14.4‑188)
(14.4‑189)
where
\(L_{\text{ls}}\) and \(L_{\text{us}}\) are the lengths of the lower and upper slug, respectively.
The calculation of the velocities of the interfaces between liquid slugs and interaction region is based on the basic physics equation stating that force is equal to the rate of momentum change. This is applied to a shock front crossing the interface that is driven by a pressure difference \(\Delta P\):
(14.4‑190)
where
(14.4‑191)
For this equation, the mass accelerated to velocity \(u_{\text{if}}\) per \(\Delta t\) is the mass which was crossed by the shock wave during \(\Delta t\). This mass is accelerated through a velocity increment of \(\left\lbrack u_{\text{if}} - u_{\text{if}} \left( t_{\text{o}} \right) \right\rbrack\) due to the crossing of the shock. By inserting Eq. 14.4-191 into Eq. 14.4-190, one obtains:
(14.4‑192)
For \(u_{\text{if}} \left( t_{\text{o}} \right) = 0\), this would be equal to the first Rankine-Hugoniot condition for shock waves [14-56] if the actual shock velocity rather than the sonic limit were used.
The above equation is used for the velocity calculation of the lower slug interface during the acoustic period (see Eq. 14.4-188):
(14.4‑193)
In this equation, the definition of the velocity of sound (14.4-187) and time-dependent interface pressure were introduced. To use a time-dependent pressure is not in the spirit of Eq. 14.4-192 which assumes a constant pressure difference. This represents the main assumption of the acoustic approximation in PLUTO2. Comparison calculations with the fully compressible PLUTO code [14.3, 14-4] have shown that it is a reasonable assumption. For the velocity calculation of the upper slug, the following is used during the acoustic period:
(14.4‑194)
After the acoustic period for the lower slug is over (see Eq. 14.4-188), the incompressible calculation of the lower slug mass flow rate begins. For the upper slug, this calculation starts after the time calculated by Eq. 14.4-189 has been exceeded.
A separate incompressible slug calculation is done for the lower sodium slug (below the interaction region) and for the upper slug (above the interaction region). These slugs can occupy several axial channel zones. Each channel zone is characterized by its input flow cross section, hydraulic diameter and axial length. The sodium slugs can fully extend over several channel zones, but the uppermost segment of the lower slug and the lowermost segment of the upper slug do not fully cover a channel zone because of the presence of the interaction region. The length of the uppermost segment of the lower slug and the lowermost segment of the upper slug can vary because they have moving boundaries. A control volume approach for the momentum balance of one slug segment yields (after taking into account the assumption of a constant density in the entire lower or upper slug):
(14.4‑195)
where the last three terms describe entrance and exit losses and the losses due to grid spacers in this slug segment and
\(L_{\text{i}}\) = length of slug segment \(i\)
\(A_{\text{ch,i}}\) = cross section of slug segment \(i\)
\(F_{\text{i}} = 1\) except \(i\) designates the lower (moving) interface of the upper slug. In this case, \(F_{\text{i}} = 0\).
\(F_{\text{i+1}} = 1\) except when \(i+1\) designates the upper (moving) interface of the lower slug. In this case, \(F_{\text{i+1}} = 0\).
The left-hand side of Eq. 14.4-195 can be rewritten as
(14.4‑196)
The \(\frac{\Delta L_{\text{i}}}{\Delta t}\) is only non-zero for the uppermost segment of the lower slug and the lowermost segment of the upper slug. For the case of these two special slug segments:
(14.4‑197)
(14.4‑197a)
For slug segments that are neither the uppermost one of the lower slug nor the lowermost one of the upper slug, the two convective terms in Eq. 14.4-195 cancel because the velocity is the same everywhere in a slug segment. For the uppermost segment of the lower slug, only the second convective term is present in Eq. 14.4-195 and this one cancels with the last term of the right-hand side of Eq. 14.4-196. For the lowermost segment of the upper slug, only the first convective term is present in Eq. 14.4-195. This one cancels also with the last term in Eq. 14.4-196 because of Eq. 14.4-197a, which holds in this case.
After inserting Eq. 14.4-196 into Eq. 14.4-195, cancelling the convective terms and the terms with \(\frac{\Delta L_{\text{i}}}{\Delta t}\) (see above discussion), and after dividing the new equation with \(A_{\text{ch,i}}\), all the segment equations for each of the two slugs are added up. For the lower slug, this lead to:
(14.4‑198)
where
\(W_{\text{ls}} = \rho_{\text{N1,ls}} A_{\text{ch,i}} u_{\text{N1,i}}\), the mass flow rate which is the same in all segments of the lower slug because of the assumed incompressibility
\(\text{IB}\) = index of the uppermost segment of the lower slug
\(P_{\text{ch,IB}}\) = pressure in the first node of the interaction region
\(\Delta P_{\text{zi}}\) = pressure drop due to the area change between segment \(i-1\) and segment \(i\) or due to an orifice at the bottom of segment \(i\). This pressure drop is evaluated from
(14.4‑199)
where \(\text{XKORV}_{\text{i,m}}\) is the input contraction or expansion coefficient for upward or downward flow. This can also be an orifice coefficient for segment \(i\). Coefficients with \(m = 1\) are used for upward flow; coefficients with \(m = 2\) for downward flow, \(\Delta P_{\text{or,ls}}\) is the pressure drop due to grid spacers in the channel zone KZPIN and is evaluated from the equation
(14.4‑200)
where
\(\text{KZPIN}\) = the channel zone which contains the pins
\(\text{XKORGD}\) = an input pressure-drop coefficient for a single grid spacer
(14.4‑200a)
where
NGRDSP = the number of uniformly distributed grid spacers in the channel zone KZPIN which is input.
\(Z_{\text{ls,if}}\) = axial location of the lower slug interface
\(Z_{\text{i=KZPIN}}\) = location of the lower boundary of channel zone KZPIN
For the upper sodium slug, the incompressible momentum equation is
(14.4‑201)
where
\(\text{IT}\) = index of the lowermost segment of the upper slug
\(\text{IMAX}\) = index of the top segment of the upper slug
The reason for performing the slug momentum calculations is to determine the upper and lower interface velocities of the interaction region:
(14.4‑202)
and
(14.4‑203)
where
\(A_{\text{IB}}\) = the flow area of the uppermost segment of the lower slug
\(A_{\text{IT}}\) = the flow area of the lowermost segment of the upper slug.
14.4.6.4. PLUTO2 Time Step Determination¶
The PLUTO2 time step \(\Delta t_{\text{PL}}\) used in the numerical marching of all the in-pin and channel conservation equations is restricted by the sonic Courant conditions for both the in-pin and the channel flows. An upper limit \(\Delta t_{\text{PL,pin}}\) of the PLUTO2 time step computed, based on the sonic Courant condition for the in-pin flow of the fuel and fission gas two-phase mixture, is given in Section 14.2.8. In the present section, another upper limit \(\Delta t_{\text{PL,ch}}\) of the PLUTO2 time step is computed based on the sonic Courant condition for the multi-component channel flow, and then the smaller of the two upper limits gives the PLUTO2 time step \(\Delta t_{\text{PL}}\). The upper limit \(\Delta t_{\text{PL,ch}}\) is computed to be a fraction, 0.4, (same as that used in computing \(\Delta t_{\text{PL,pin}}\)) of the minimum time step based on the sonic Courant condition for the channel flow.
(14.4‑204)
The minimum in Eq. 14.4-204 is evaluated over all axial cells of the interaction region. The sonic velocity in the channel is calculated from an equation [14-28] for an adiabatic homogeneous two-phase mixture of liquid sodium and fission gas/sodium vapor. The compressibility of liquid fuel being much smaller than that of liquid sodium, the fuel is assumed to be incompressible in the calculation of the sonic velocity in the channel. The effect of fuel vapor is also not included.
(14.4‑205)
where
\(\alpha_{\text{vg}} = \frac{\theta_{\text{vg}}}{\left( \theta_{\text{ch,op}} - \theta_{\text{fu}} \right)}\) = void fraction in the two-phase mixture of liquid sodium and fission gas/sodium vapor.
\(\gamma_{\text{vg}}\) = ratio of specific heat at constant pressure to that at constant volume of the fission gas/sodium vapor mixture. A value of 1.4 is assumed in the PLUTO2 code.
\(K_{\text{N1}} = \text{MNL}\) = adiabatic compressibility of liquid sodium.
The fission-gas pressure \(P_{\text{fi}}\) and pressure \(P_{\text{Nv}}\) due to sodium vapor are obtained as explained in Section 14.4.5 using the following equations.
(14.4‑206)
(14.4‑207)
After evaluating the two upper limits \(\Delta t_{\text{PL,pin}}\) and \(\Delta t_{\text{PL,ch}}\) using Eqs. 14.2-55 and 14.4-204, the PLUTO2 time step \(\Delta t_{\text{PL}}\) is taken to be the smaller of the two.
(14.4‑208)
If the value of \(\Delta t_{\text{PL}}\) obtained from Eq. 14.4-208 is less than the minimum time step given by the input parameter DTPLIN (suggested value \(2.5 \times 10^{-5}\) s), then \(\Delta t_{\text{PL}}\) is set equal to DIPLIN. Also, the PLUTO2 time step \(\Delta t_{\text{PL}}\) is not allowed to exceed a maximum value of \(2 \times 10^{-4}\) s (a number built in the code). The value of \(\Delta t_{\text{PL}}\) obtained in this way is rounded to an integral multiple of \(1.0 \times 10^{-5}\) s. The PLUTO2 time steps are not allowed to span the coolant dynamics time-step boundaries, or the heat-transfer time-step boundaries, or the primary loop time-step boundaries.
Footnotes