7.2. Network Thermal/Hydraulic Model

7.2.1. Discretization of the Balance of Plant

SASSYS-1 represents the balance of plant as a network of one-dimensional flow paths which are joined at flow junctions. Junctions are of two types; those in which there is no separation of liquid and vapor (in which case perfect mixing is assumed) and those in which liquid and vapor are strictly separated (in which case instantaneous separation and saturation conditions are assumed). As a result of using this representation, the mass, momentum, and energy equations that describe the system can be reduced to one-dimensional forms. The network of junctions and paths is just a discretization of the balance of plant using a non-uniform spatial mesh; the network is perhaps best described as a nodalization of the plant. The momentum equation is solved along each flow path, and the mass and energy equations are solved at each flow junction. Flow is assumed uniform throughout each flow path. Because the junctions are regions of fixed volume and are used in part to model compressibility effects in the system, they are given the name compressible volumes. Flow paths are known simply as flow segments.

The balance of plant is a collection of several types of components: pipes, valves, check valves, pumps, heaters, inlet and outlet plena, and piping junctions. The steam generator is intentionally omitted form this list, since it is treated as a separate model (Section 7.3). Components which primarily affect mass flow rate and pressure drop in a flow segment are best described through the momentum equation and are modelled as sections of flow segments; these sections are called flow elements. The cross-sectional area is constant throughout a given flow element. Element types include pipes, valves, check valves, and pumps. Flow segments then become strings of one or more flow elements; for example, a flow segment might consist of a length of pipe (element 1), followed by a pump (element 2), followed by a check valve (element 3). The flow would be the same in all three elements, but the geometry could differ from element to element.

Components which join two or more flow segments are best described through the mass and energy equations and are modelled as compressible volumes; these include inlet and outlet plena, piping junctions, and open heaters. Closed heaters must be described through a combination of flow elements and a compressible volume (Section 7.4).

More detailed information about constructing a nodalization of a plant will be presented in Section 7.2.7.

7.2.2. Analytical Equations

The general analytical equations are

(7.2-1)\[\text{mass: } \frac{\partial \rho}{\partial t} = - \left(\boldsymbol{\nabla} \cdot \rho \mathbf{u} \right)\]

(7.2-2)\[\text{momentum: } \frac{\partial}{\partial t} \left(\rho \mathbf{u}\right) = -\left[ \boldsymbol{\nabla} \cdot \rho \mathbf{u} \mathbf{u} \right] - \boldsymbol{\nabla} P - \left[\boldsymbol{\nabla} \cdot \boldsymbol{\tau} \right] + \rho \mathbf{g}\]

(7.2-3)\[\text{energy: } \frac{\partial}{\partial t} \left(\rho \hat{E} \right) = - \left( \boldsymbol{\nabla} \cdot \rho \overline{E} \mathbf{u} \right) - \boldsymbol{\nabla} \cdot \mathbf{q} - \left[ \boldsymbol{\nabla} \cdot P \mathbf{u} \right] - \left[ \boldsymbol{\nabla} \cdot \left( \boldsymbol{\tau} \cdot \mathbf{u} \right) \right]\]

These can be simplified by making the following assumptions:

1. One-dimensional flow,

2. Neglect the work done by viscous forces on a compressible volume (this is the \(\boldsymbol{\nabla} \cdot \left( \boldsymbol{\tau} \cdot \mathbf{u} \right)\) term in Eq. (7.2-3)),

3. Neglect kinetic energy and gravitation energy,

4. The viscous term in the momentum equation can be expressed as \(\frac{F \rho u \left| u \right|}{2}\).

In addition, if the total energy (which is now assumed to equal the internal energy) is expressed in terms of the enthalpy, the mass, momentum, and energy equations take the simpler forms

(7.2-4)\[\text{mass: }\frac{\partial\rho}{\partial t} = - \frac{\partial\rho u}{\partial z}\]

(7.2-5)\[\text{momentum: } \frac{\partial\rho u}{\partial t} = - \frac{\partial\rho u^{2}}{\partial z} - \frac{\partial P}{\partial z} - F\frac{\rho u \left| u \right|}{2} + \rho gcos\theta\]

(7.2-6)\[\text{energy: } \frac{\partial\rho h}{\partial t} = - \frac{\partial\rho hu}{\partial z} - \frac{\partial q}{\partial z} + \frac{\partial P}{\partial t}\]

The system is closed by using an equation of state; for single-phase fluid, this takes the form

(7.2-7)\[\frac{\partial v}{\partial t} = \left( \frac{\partial v}{\partial P} \right)_{h} \frac{dP}{dt} + \left( \frac{\partial v}{\partial h} \right)_{P} \frac{dh}{dt}\]

while for two-phase fluid, the equation of state is

(7.2-8)\[\frac{\partial v}{\partial t} = \left( \frac{\partial v}{\partial P} \right)_{h} \frac{dP}{dt} + \left( \frac{\partial v}{\partial x} \right)_{P} \frac{dx}{dt}\]

The coefficient \(F\) in the momentum equation needs further explanation. The term \(F \rho \vert u \vert| / 2\) accounts for pressure losses along the flow path due to friction, bends, area changes, and orifices or baffles. The coefficient \(F\) is the sum of three factors:

1. the frictional factor, \(fL/D_{h}\), with \(L\) the flow element length, \(D_{h}\) the element hydraulic diameter, and \(f\) the friction factor. For turbulent single-phase flow, \(f\) is the Moody friction factor

(7.2-9)\[f = C_{1} \bigg\{ 1 + \left( C_{2} \frac{\varepsilon}{D_{h}} + \frac{C_{3}}{Re} \right)^{C_{4}}\]

where C1 - C4 are constants (see Ref. 7-1), \(\varepsilon\) is the element roughness, and \(Re\) is the Reynolds number,

(7.2-10)\[Re = \frac{D_{h} \vert w \vert}{A \mu}\]

with \(\mu\) the fluid dynamic viscosity. For laminar single-phase flow, \(f\) is calculated from

(7.2-11)\[f = 64 / Re\]

2. the term \(f\left( L_{B}/D_{B} \right)N_{B}\), which accounts for pressure losses due to bends. Here, \(N_B\) is the number of bends along the flow path, and the term (\(L_{B}/D_{B}\)) is the effective length-to-diameter ratio per bend. The same value is used for (\(L_{B}/D_{B}\)) on the water side as is used on the sodium side. The friction factor \(f\) is the same one just described in 1).

3. the orifice coefficient, \(G_{2}\). There is no formalism for independently calculating the initial value of \(G_{2}\); in the SASSYS-1 balance-of-plant coding, this coefficient is usually calculated by the code in the steady-state initialization so as to balance the remaining terms in the momentum equation. During the transient calculation, \(G_{2}\) will vary as orifices change size (e.g., a valve opening or closing). A detailed explanation of how \(G_{2}\) is computed for various types of components is presented in Section 7.2.3.2 below.

The factor \(F\) is then defined as

(7.2-12)\[F = f \left( L / D_{h} \right) + f \left( L_{B} / D_{B} \right) N_{B} + G_{2}\]

In the case of two-phase flow, \(F\) is still given by Eq. (7.2-12), but now a two-phase friction correlation must be used rather than the single-phase expression of Eq. (7.2-9) and Eq. (7.2-11). The question of modelling pressure drop in a two-phase flow has been examined at length in the literature. The approach taken in the balance-of-plant model is that set forth by Thom in Ref. 7-2, in which he describes a homogeneous equivalent model which makes use of two-phase multipliers to adjust the homogeneous gravitational, acceleration, and frictional pressure drop terms to accommodate general two-phase flow. The assumption is made in the balance-of-plant model that slip between the phases can be neglected. In this case, Ref. 7-2 shows that the gravitational and acceleration terms keep the same forms as for single-phase flow, with the appropriate mixture densities used. The same is assumed to be true for the orifice term. The frictional term is adjusted by multiplying the single-phase liquid friction factor by an empirically-determined two-phase multiplier. This multiplier adjusts the pressure drop computed for saturated liquid at a specific flow and pressure to give the pressure drop corresponding to two-phase flow at the same pressure and mass flow rate. The multiplier is a function of both quality and pressure.

Reference 7-2 presents a table of the two-phase multiplier appropriate to flow through an unheated pipe. The multiplier is given at discrete values of pressure from 250 to 3000 psi and at qualities between 0 and 1. These values were used to develop an expression to be used in the balance-of-plant model for the two-phase multiplier \(r_{5}\) as a function of pressure and quality. The expression was derived using the method of least squares; it has the form

(7.2-13)\[r_{5} = 0.9124 + 0.198 \overline{P} + x \left(-7.38 + 108.7 \overline{P} - 4.166 \overline{P}^{2} \right)\]

where the pressure \(P\) is in psi, \(\overline{P} = P / 250\) and \(x\) is the quality. This expression is accurate to 11% or better for all qualities and for pressures between 250 and 3000 psi; at most points, it is accurate to better than 5%. The two-phase friction factor \(f_{tp}\) is then just

(7.2-14)\[f_{tp} = r_{5} f_{l}\]

7.2.3. Discretized Equations

The analytical forms of the mass, momentum, and energy equations and the equation of state now need to be discretized over the compressible volumes and flow elements of the balance-of-plant nodalization. The result of the discretization will be a set of fully implicit equations which can be solved simultaneously for the changes in pressure, flow, and enthalpy in a timestep. All other quantities (e.g., densities, heat sources) will be computed explicitly.

The first step is to use the momentum equation to express the change over a timestep in the mass flow rate in each segment as a function of the changes in the segment endpoint pressures. Next, the mass and energy equations and the equation of state can be combined to express the change in pressure within a compressible volume as a function of the changes in the flows of all segments which are attached to the volume. If these two sets of equations are combined by eliminating the change in flow, the resulting matrix equation can be solved for the change in pressure in each compressible volume. The changes in flow and enthalpy, as well as the changes in all explicit variables, can then be determined.

7.2.3.1. Discretization of the Momentum Equation

The momentum equation is discretized segment by segment. In order to represent momentum transport correctly through a segment made up of more than one flow element, the momentum equation must be integrated along the length of the segment, giving

(7.2-15)\[\begin{split}\sum_{k}^{}{\frac{L_{k}}{A_{k}}\frac{\partial w}{\partial t} = P_{in} - P_{out} - \sum_{k}^{}{\frac{w^{2}}{A_{k}^{2}}\left\lbrack \frac{1}{\rho_{O_{k}}} - \frac{1}{\rho_{I_{k}}} \right\rbrack}} \\ - \sum_{k}^{}{F\left( k \right)\frac{w\left| w \right|}{2{\overline{\rho}}_{k}A_{k}^{2}} - \overline{\rho}g(z_{out} - z_{in})}\end{split}\]

where the summation is over all elements in a segment. The form of Eq. (7.2-15) is valid for all element types except pumps; the convective and viscous terms have a different form for pumps, and Eq. (7.2-15) is modified accordingly when a flow segment contains a pump.

The momentum equation must also be discretized over time. The right-hand side of Eq. (7.2-15) is a function only of flow and time and is the net pressure imbalance across the segment, labelled \(\Delta P_{\text{net}}(w,t)\). If Eq. (7.2-15) is differenced over a timestep \(\Delta t = t^{n + 1} - t^{n}\), with \(\Delta P_{net}(w,t)\) chosen at the advanced time \(t^{n + 1}\) and then linearized, the result is

(7.2-16)\[\sum_{k} \frac{L_{k}}{A_{k}} \Delta w = \Delta t \left\{ \Delta P_{net} \left( w, t \right) + \left[ \Delta t \left(\frac{\partial \Delta P_{net}}{\partial t} \right)_{w} + \Delta w \left( \frac{\partial \Delta P_{net}}{\partial w} \right)_{t} \right] \right\}\]

If \(\Delta P_{net}\) in Eq. (7.2-17) is replaced with the right-hand side of Eq. (7.2-15) and terms are rearranged, the result is an expression for the change in segment flow, \(\Delta w\) as a function of \(\Delta P_{in}\) and \(\Delta P_{out}\), the changes in pressure at the segment inlet and outlet, respectively:

(7.2-17)\[\Delta w = \frac{a_{1} + \left[a_{2} + \Delta t \left(\Delta P_{in} - \Delta P_{out} \right) \right]}{\left( a_{0} - a_{3} \right)}\]

where

(7.2-18)\[ \begin{align}\begin{aligned}a_{0} &= \sum_{k} \frac{L_{k}}{A_{k}}\\a_{1} &= {\Delta}t\left\lbrack P_{in}\left( t \right) - P_{out}\left( t \right) \right\rbrack + \sum_{k}^{}{{\Delta}a_{1}\left( k \right)}\end{aligned}\end{align} \]

(7.2-19)\[{\Delta}a_{1}\left( k \right) = - {\Delta}t\left\{ \frac{w^{2}}{A_{k}^{2}}\left\lbrack \frac{1}{\rho_{O_{k}}} - \frac{1}{\rho_{I_{k}}} \right\rbrack - F\left( k \right)\frac{w\left| w \right|}{2{\overline{\rho}}_{k}A_{k}^{2}} - {\overline{\rho}}_{k}g{\Delta}z_{k} \right\}\]

(7.2-20)\[a_{2} = \sum_{k} \Delta t \frac{\partial}{\partial t} \left(\Delta a_{1} \left( k \right) \right)\]

(7.2-21)\[a_{3} = \sum_{k} \frac{\partial}{\partial w} \left( \Delta a_{1} \left( k \right) \right)\]

7.2.3.2. Further Details on Element Component Models

The discretized momentum equation, Eq. (7.2-17), models flow along a one-dimensional flow path. The path can contain bends, baffles or orifices, and the cross-sectional area of the path can vary. This flow path model serves as the basis for the models for pipes, valves, and check valves. What distinguishes these three component models is the way in which the coefficient \(F\) is varied with time. The only contributors to \(F\) which may vary with time are the friction factor and the size of a flow orifice. The friction factor is treated identically in all component models, and so the differences among component models are determined by the way in which each model calculates the orifice coefficient.

The model of a pipe assumes that the orifice coefficient calculated in the steady state is valid through the transient. Therefore, the pipe model keeps the orifice coefficient constant at all times. The valve models, on the other hand, simulate the opening and closing of the valve by varying the orifice coefficient. The pressure drop across a valve is related to the flow through the valve by the equation

(7.2-22)\[\Delta P = \frac{w \vert w \vert}{\rho C^{2} \phi ^{2} \left( y \right)}\]

The functional relationship between the valve characteristic \(\phi\) and the stem position \(y\) depends on the valve design and is input by the user through tables. The valve is opened or closed by varying the stem position; the user has the option of adjusting \(y\) directly or through the harmonic equation

(7.2-23)\[m \frac{d^{2} y}{dt^{2}} + B \frac{dy}{dt} + ky = F_{1} \left( t \right)\]

so that \(y\) is controlled by the driver function \(F_{1} \left( t \right)\), which is user-input. Since the pressure drop across the valve is related to the orifice coefficient \(G_{2}\) by

(7.2-24)\[\Delta P = G_{2} \frac{w \vert w \vert}{2 \rho A^{2}}\]

where \(A\) is the flow area when the valve is fully open, the orifice coefficient can be expressed in terms of the valve calibration constant and characteristic as

(7.2-25)\[G_{2} = 2 \left( \frac{A}{C \phi} \right)^{2}\]

Thus, the valve aperture changes by recomputing the orifice coefficient each timestep, and the value of the coefficient is controlled by the stem position.

The check valve model works much the same as the standard valve model. However, there are a few differences. A check valve is normally either completely open or completely closed, whereas a standard valve can operate partially closed. A check valve changes between open or closed when a user-specified flow or pressure drop criterion within the valve is met. The valve then changes state by adjusting the orifice coefficient to a user-input value within a span of time that is also user-input. The criteria for opening and closing the valve, as well as the length of time the valve takes to open or close, must be set so as to avoid creating numerical instabilities in the calculation.

Because both valve models simulate valve closure by setting the orifice coefficient to a very large value, the flow through a valve in never actually zero. However, if the orifice coefficient is set sufficiently large, the resulting flow through the valve will be negligible.

Modelling pumps must be approached in a different way from that used in modelling pipes, valves, and check valves, since the convective and viscous terms are no longer simple functions of the mass flow rate. The head/flow relationships represented by these terms are instead described by a set of homologous pump curves. Two types of pump curves are available in the balance-of-plant model, one using polynomial fits and one using more complex functional forms. Both options are identical to the corresponding options used in SASSYS-1 for sodium pumps. See Chapter 5 for details of the pump models.

Superheaters are simply steam-filled pipes in which heat transfer is occurring along the length of the pipe. The balance-of-plant model therefore simulates a superheater as a pipe for which the orifice coefficient and the lengthwise-averaged enthalpy, temperature, and density are computed explicitly by a separate superheater model. The superheater model is similar to the steam generator evaporator model, except that no phase change occurs in a superheater. A detailed description of the superheater model is given in Section 7.3.

7.2.3.3. Discretization of the Mass and Energy Equations and the Equation of State

The derivation that follows assumes perfect mixing within a compressible volume. Volumes in which liquid and vapor are separated are discussed in Section 7.4.

The mass and energy equations and the equation of state are solved at each compressible volume. Because the fluid within each volume is assumed to be perfectly mixed, the enthalpy and pressure are uniform within a volume (neglecting the pressure variations due to gravitational head). Therefore, the energy equation can be discretized in space by integrating Eq. (7.2-6) over each volume l and writing a separate energy equation for each volume,

(7.2-26)\[V_{l} \frac{\partial \left(\rho_{l} h_{l} \right)}{\partial t} = - V_{l} \nabla \left( \rho u h \right)_{l} + Q_{l} + V_{l} \frac{\partial P_{l}}{\partial t}\]

where \(Q_{l}\) is the net rate at which heat enters volume \(l\). Eq. (7.2-26) will be easier to work with if density and velocity are eliminated and the equation is rewritten in terms of flows and masses. This is accomplished by using the simple relationship between mass and density, \(\rho V = m\), and recognizing that the enthalpy convection term is just the rate at which enthalpy is convected into the volume, so that

(7.2-27)\[V_{l} \nabla \left( \rho u h \right)_{l} = - \sum_{j} h_{j} w_{j} \text{sgn} \left(j, l \right)\]

where the sum is over all segments which are attached to volume \(l\). Substituting in Eq. (7.2-26) for the convective term and density gives the desired form of the energy equation,

(7.2-28)\[\frac{\partial\left( m_{l}h_{l} \right)}{\partial t} = \sum_{j}^{}{h_{j}w_{j} \text{sgn}(j,l)} + Q_{l} + V_{l}\frac{\partial P_{l}}{\partial t}\]

Now, the time derivative of the total enthalpy \(m_{l} h_{l}\) needs to be expanded so that the time derivatives of the mass and the specific enthalpy can be handled separately. To do this, three operations are performed: 1) the derivative of the total enthalpy in Eq. (7.2-28) is discretized over time, 2) the advanced time terms are linearized, and 3) second-order terms are dropped. The result is

(7.2-29)\[\frac{\partial m_{l}}{\partial t} h_{l}^{n} \frac{\partial h_{l}}{\partial t} = \sum_{l} h_{l}^{n + 1} w_{j}^{n + 1} \text{sgn}\left(j, l \right) + Q_{l}^{n} + V_{l} \frac{\partial P_{l}}{\partial t}\]

This form of the energy equation is a linear function of the volume mass, enthalpy, and pressure and of the enthalpies and flows from the segments attached to the volume. The heat source \(Q\) is assumed to be treated explicitly, and the enthalpy convection term is evaluated at the advanced time.

The next step is to eliminate the mass time derivative from the energy equation. This is done by using the mass conservation equation written for volume \(l\) and multiplied by the volume \(V_{l}\),

(7.2-30)\[V_{l} \frac{\partial \rho _{l}}{\partial t} = - V_{l} \frac{\partial}{\partial z} \left( \rho u \right)_l\]

The left-hand side of Eq. (7.2-30) is just the time derivative of the mass, and the right-hand side is the mass convection term, which is just the net flow into the volume, so that Eq. (7.2-30) can be rewritten as

(7.2-31)\[\frac{\partial m_{l}}{\partial t} = \sum_{j} w_{j} \text{sgn} \left(j, l \right)\]

Eq. (7.2-31) is just the expression needed to eliminate the mass time derivative from the energy equation; when it is substituted into Eq. (7.2-29), the result is

(7.2-32)\[m_{l}^{n}\frac{\partial\left( h_{l} \right)}{\partial t} = - h_{l}^{n}\sum_{j}^{}{w_{j}^{n + 1}\text{sgn}\left( j,l \right)} + \sum_{j}^{}{{h_{j}^{n + 1}w}_{j}^{n + 1}\text{sgn}\left( j,l \right)} + Q_{l}^{n} + V_{l\ }\frac{\partial P_{l}}{\partial t}\]

There is one difficulty with the form of the energy equation shown in Eq. (7.2-32) – the enthalpies at the interfaces between the compressible volume and the attached flow segments are treated implicitly. For the range of problems for which this model has been developed, treating these enthalpies explicitly introduces only small errors at worst. Treating them implicitly results in a solution procedure which is unnecessarily complicated and cumbersome. Therefore, it is assumed that these enthalpies can be treated explicitly. Applying this assumption to Eq. (7.2-32) and also finite differencing the time derivatives and linearizing the advanced time flows produces an energy equation of the form

(7.2-33)\[\begin{split}m_{l}^{n} \frac{\Delta h_{l}}{\Delta t} = -h_{l}^{n} \sum_{j} \left(w_{j}^{n} + \Delta w_{j} \right) \text{sgn} \left(j, l \right) + \sum_{j} h_{j}^{n} \left(w_{j}^{n} + \Delta w_{j} \right) \text{sgn} \left(j, l \right) \\ + Q_{l}^{n} + V_{l} \frac{\Delta P_{l}}{\Delta t}\end{split}\]

Eq. (7.2-33) expresses the change in volume enthalpy as a function of the change in volume pressure and the changes in flow in the attached segments. If the change in enthalpy can be eliminated, the result will be an equation relating the change in volume pressure to the changes in the segment flows. This can then be combined with the expression derived from the momentum equation which relates the change in flow in a segment to the changes in pressure in the volumes at the segment endpoints, producing a matrix equation which can be solved for the pressure changes in the compressible volumes in the system.

The change in volume enthalpy can be eliminated from Eq. (7.2-33) by using the equation of state, Eq. (7.2-7) and Eq. (7.2-8) above. Consider first the case of a volume containing single‑phase fluid. The equation of state is then Eq. (7.2-7). An expression for the change in volume enthalpy can be derived from Eq. (7.2-7) if the time derivative of the specific volume is rewritten as

(7.2-34)\[\frac{\partial v}{\partial t} = - v^{2} \left( \frac{\partial \rho }{\partial t} \right) = - \frac{v^{2}}{V} \frac{\partial m}{\partial t} = -\frac{v^{2}}{V} \sum_{j} \left(w_{j} + \Delta w _{j} \right) \text{sgn} \left(j, l \right)\]

Therefore, the equation of state takes the form

(7.2-35)\[- \frac{v_{l}^{2}}{V_{l}} \sum_{j} \left(w_{j}^{n} + \Delta w_{j} \right) \text{sgn} \left(j, l \right) = \left( \frac{\partial v_{l}}{\partial P} \right)_{h}^{n} \frac{\Delta P_{l}}{\Delta t} + \left( \frac{\partial v_{l}}{\partial h} \right)_{P}^{n} \frac{\Delta h_{l}}{\Delta t}\]

where the remaining time derivatives have been finite differenced. Eq. (7.2-35) is another expression for the change in volume enthalpy as a function of the change in volume pressure and the changes in the segment flows and so can be substituted into the energy equation, Eq. (7.2-33), to eliminate the change in volume enthalpy, giving

(7.2-36)\[\begin{split}-\frac{\left( v_{l}^{n} \right)^{2}}{V_{l}} \sum_{j} \left(w_{j}^{n} + \Delta w_{j} \right) \text{sgn}\left(j, l \right) = \left( \frac{\partial v_{l}}{\partial P} \right)_{h}^{n} \frac{\Delta P_{l}}{\partial t} + \left( \frac{\partial v_{l}}{\partial h} \right)_{P}^{n} \frac{1}{m_{l}^{n}} \\ \times \bigg\{ -h_{l}^{n} \sum_{j} \left(w_{j}^{n} + \Delta w_{j} \right) \text{sgn}\left(j, l \right) + \sum_{j}h_{j}^{n} \left( w_{j}^{n} + \Delta w \right) \text{sgn} \left(j, l \right) \\ + Q_{l}^{n} + V_{l} \frac{\Delta P_{l}}{\Delta t} \bigg\}\end{split}\]

If the mass of volume \(l\) is expressed in terms of \(V_{l}\) and \(\rho _{l}\) and the equation is then rearranged, the result is an equation for the change in volume pressure as a function of the changes in the segment flows:

(7.2-37)\[\begin{split}\Delta P_{l} = -\Delta t \bigg\{ Q_{l}^{n} + \sum_{j} w_{j}^{n} \left[ h_{j}^{n} - h_{l}^{n} + v_{l}^{n} \left( \frac{\partial h_{l}}{\partial v} \right)_{P}^{n} \right] \text{sgn} \left(j, l \right) \\ + \sum_{j} \Delta W_{j} \left[h_{j}^{n} - h_{l}^{n} + v_{l}^{n} \left( \frac{\partial h_{l}}{\partial v} \right)_{P}^{n} \right] \text{sgn} \left(j, l \right) \bigg\} / \\ \left[V_{l} \left(1 + \frac{1}{v_{l}^{n}} \left( \frac{\partial v_{l}}{\partial P} \right)_{h}^{n} \left( \frac{\partial h_{l}}{\partial v} \right)_{P}^{n} \right) \right]\end{split}\]

If volume \(l\) contains two-phase fluid, the equation of state must be expressed by Eq. (7.2-8), and the resulting equations are more complex. In the case of a two‑phase fluid, the specific volume is a function of pressure and quality, rather than pressure and enthalpy, and so Eq. (7.2-8) cannot be used directly to derive an expression for the change in enthalpy. Instead, the following approach must be taken.

The saturated liquid specific volume and enthalpy can be written respectively as

(7.2-38)\[v_{l} = v_{f} + \left(v_{g} - v_{f} \right) x_{l} = v_{f} + v_{fg} x_{l}\]

and

(7.2-39)\[h_{l} = h_{f} + h_{fg} x_{l}\]

Differencing Eq. (7.2-38) with respect to time gives

(7.2-40)\[\frac{dv_{l}}{dt} = \frac{dv_{f} \left( l \right)}{dt} + x_{l} \frac{dv_{fg} \left( l \right)}{dt} + v_{fg} \left( l \right) \frac{dx_{l}}{dt}\]

Since the saturated liquid and vapor specific volumes are functions only of pressure, Eq. (7.2-40) can be rewritten in terms of the time derivative of pressure,

(7.2-41)\[\frac{dv_{l}}{dt} = \frac{dP_{l}}{dt} \frac{dv_{f} \left( l \right)}{dP} + x_{l} \frac{dP_{l}}{dt} \frac{dv_{fg}\left( l \right)}{dP} + v_{fg} \left( l \right) \frac{dx_{l}}{dt}\]

Similarly, Eq. (7.2-39) can be expressed as

(7.2-42)\[\frac{dh_{l}}{dt} = \frac{dP_{l}}{dt} \frac{dh_{f} \left( l \right)}{dP} + x_{l} \frac{dP_{l}}{dt} \frac{dh_{fg} \left( l \right)}{dP} + h_{fg} \left( l \right) \frac{dx_{l}}{dt}\]

The time derivative of quality can be eliminated between Eq. (7.2-41) and Eq. (7.2-42) to give

(7.2-43)\[\begin{split}\frac{dv_{l}}{dt} = - \frac{v_{l}^{2}}{V_{l}} \sum_{j} w_{j}^{n+1} \text{sgn} \left(j, l \right) = \frac{dP}{dt} \bigg[ \frac{dv_{f}\left(l\right)}{dP} + x_{l} \frac{dv_{fg} \left( l \right)}{dP} \\ - \left( \frac{dh_{f} \left( l \right)}{dP} + x_{l} \frac{dh_{fg}\left( l \right)}{dP} \right) \frac{v_{fg} \left(l \right)}{h_{fg}\left( l \right)} \bigg] + \frac{dh_{l}}{dt} \frac{v_{fg} \left( l \right)}{h_{fg} \left( l \right)}\end{split}\]

Eq. (7.2-43) can be used in place of Eq. (7.2-8) to give an expression for the change in volume enthalpy in a two‑phase volume. This expression can then be used in the same manner that Eq. (7.2-35) was used above, producing an equation for the change in volume pressure as a function of the changes in the flows in the attached segments:

(7.2-44)\[\begin{split}\Delta P_{l} = - \Delta t \bigg\{ Q_{l}^{n} + \sum_{j} w_{j}^{n} \left[ h_{j}^{n} - h_{l}^{n} + v_{l}^{n} \frac{h_{fg} \left( l \right)}{v_{fg} \left( l \right)} \right] \text{sgn} \left(j, l \right) \\ + \sum_{j} \Delta w_{j} \left[h_{j}^{n} - h_{l}^{n} + v_{l}^{n} \frac{h_{fg} \left( l \right)}{v_{fg} \left( l \right)} \right] \text{sgn} \left(j, l \right) \bigg\} / \\ \bigg\{ V_{l} \bigg(1 + \frac{1}{v_{l}^{n}} \left[ \left( \frac{dv_{f} \left( l \right)}{dP} \right)^{n} + x_{l} \left( \frac{dv_{fg}}{dP} \right)^{n} \right] \frac{h_{fg} \left( l \right)}{v_{fg} \left( l \right)} \\ - \left[ \left( \frac{dh_{f}\left( l \right)}{dP} \right)^{n} + x_{l} \left( \frac{dh_{fg}}{dP} \right) \right] \bigg) \bigg\}\end{split}\]

Eq. (7.2-44) for two‑phase volumes is equivalent to Eq. (7.2-37) for single‑phase volumes.

If the terms

(7.2-45)\[\begin{split}\text{DHDN} = \left( \frac{\partial h_{l}}{\partial v} \right)_{P}^{n} \text{for } l \text{ a single-phase volume} \\ = \frac{h_{fg} \left( l \right)}{v_{fg} \left(l \right)} \text{for } l \text{ a two-phase volume}\end{split}\]

and

(7.2-46)\[\begin{split}\text{DENOM} = V_{l} \left[1 + \frac{1}{v_{l}^{n}} \left( \frac{\partial v_{l}}{\partial P} \right)_{h}^{n} \left( \frac{\partial h_{l}}{\partial v} \right)_{P}^{n} \right] \text{for } l \text{ a single-phase volume} \\ = V_{l} \bigg\{1 + \frac{1}{v_{l}^{n}} \left[ \left( \frac{dv_{f} \left( l \right)}{\partial P} \right)^{n} + x_{l} \left( \frac{ dv_{fg} \left( l \right) }{dP} \right)^{n} \right] \frac{h_{fg} \left( l \right)}{V_{fg} \left( l \right)} \\ - \left[ \left( \frac{dh_{f} \left( l \right)}{\partial P} \right)^{n} + x_{l} \left( \frac{dh_{fg}}{dP} \right)^{n} \right] \text{for } l \text{ a two-phase volume}\end{split}\]

are defined and substituted into Eq. (7.2-37) and Eq. (7.2-44), a single expression for the combined mass and energy equation can be written as

(7.2-47)\[\begin{split}\Delta P_{l} = - \Delta t \bigg\{ Q_{l}^{n} + \sum_{j} w_{j}^{n} \left[h_{j}^{n} - h_{l}^{n} + v_{l}^{n} \left( \text{DHDN} \left( l \right) \right) \right] \text{sgn}\left(j, l \right) \\ + \sum_{j} \Delta w_{j} \left[h_{j}^{n} - h_{l}^{n} + v_{l}^{n} \left( \text{DHDN} \left( l \right) \right) \right] \text{sgn} \left(j, l \right) \bigg\}\ /\ \text{DENOM}\left( l \right)\end{split}\]

7.2.3.4. Further Details Concerning Energy Transfer

Two aspects of energy transfer still have not been discussed in detail. One of these is the calculation of the heat source \(Q\) in a heater volume, and the other is the calculation of the enthalpy distribution along an unheated flow segment. These two topics will now be taken up.

7.2.3.4.1. A Simple Heater Model

Because of the wide variety of types of heaters which can be part of a power plant water side, the balance‑of‑plant model includes nine different heater representations. Eight of these are detailed models of specific types of heaters; these are the focus of most of Section 7.4, and the reader is referred to Section 7.4 for information on them. The ninth model is a very simple, basic one which is retained as an option for the user who wishes to include a heater component in a plant layout but does not want the level of detail involved in using one of the other heater models. This simple model will now be described.

The heat source \(Q\) is computed from Newton’s law of cooling in the simple heater model. The fluid on the primary side of a heater is modelled as a compressible volume and is in thermal contact with a fluid on the heater secondary side. The heater is assumed to have subcooled liquid as the primary side fluid. The secondary side is assumed to be at a uniform temperature \(T_{s}\), where \(T_{s}\) is time-dependent and is input by the user in the form of a table of temperature versus time. Neither the secondary side nor the tube separating the two sides is modelled in detail; rather, they are lumped together as a single thermal resistance which is constant throughout the transient. On the primary side, the heat transfer coefficient is computed from the Dittus-Boelter equation in the steady state and is updated during the transient from the Dittus-Boelter correlation (see Section 7.7.2).

The initialization of the heater model in the steady state begins by finding the steady‑state heat source from the net rate of enthalpy convection into the heater volume,

(7.2-48)\[Q \left( 0 \right) = \sum_{j} h_{j} w_{j}\]

where the summation is over all the segments which are attached to the volume. The total heat transfer coefficient for the heater can then be found from Newton’s law of cooling as

(7.2-49)\[h_{tot}\left( 0 \right) = \frac{Q\left( 0 \right)}{A_{ht}\left( T_{s} - T_{p} \right)}\]

Here, \(A_{ht}\) represents the heat transfer area between the primary side and the remainder of the heater and \(T_{p}\) is the temperature on the primary side (which is just the temperature of the compressible volume). The Dittus‑Boelter equation can now be used to calculate the primary side heat transfer coefficient \(h_{p} \left( 0 \right)\),

(7.2-50)\[h_{p} \left(0 \right) = 0.023 \frac{k_{p} \left( 0 \right)}{D_{hp}} \left( Re \left( 0 \right) \right)^{0.8} \left(P_{f} \left( 0 \right) \right)^{0.4}\]

The variable \(k_{p}\) is the thermal conductivity of the primary side fluid, and \(D_{hp}\) the hydraulic diameter of the primary side. Since now both the total heat transfer coefficient and the primary side one are known, the coefficient \(h_{s}\) for the remainder of the heater can be found from the relationship

(7.2-51)\[\frac{1}{h_{s}} = \frac{1}{h_{tot}} - \frac{1}{h_{p}}\]

This coefficient will then stay fixed throughout the transient. This completes the initialization of the heater model.

During the transient, the heat source is treated explicitly, so the heater model coding consists of computing a new value for \(Q\) after the pressures, flows, and enthalpies have been updated. To do this, first the current primary side heat transfer coefficient is found from the Dittus-Boelter correlation, then Eq. (7.2-51) is used to update the total heat transfer coefficient. The new value of \(Q\) can then be found from Eq. (7.2-49).

7.2.3.4.2. Modelling the Enthalpy Distribution Along a Nonheated Segment

So far, all discussion of calculation of enthalpy has been limited to the enthalpy of fluid in compressible volumes or at the interface between a volume and a segment. However, the enthalpy distribution along a segment must also be computed. This section describes the model used to find the enthalpy distribution within a nonheated segment; Section 7.3 discusses the calculation of enthalpy along the heated segment in a superheater, and Section 7.3 describes how the enthalpy distribution is calculated in the heated segment sections of heaters.

The fundamental assumption of this model is that flow within each unheated segment is adiabatic, so that there is no exchange of heat with the pipe walls, pump impellers, etc. This assumption should be valid for many types of problems and allows the enthalpy distribution to be calculated from a simple, efficient algorithm in which enthalpy is transported from one compressible volume to another. The enthalpy at any point in a segment can be found just by tracking the movement of fluid through the segment over each timestep.

Two assumptions are made in order to initialize the enthalpy distribution along each segment. First, it is assumed that the temperature is constant along each subcooled liquid segment and that this temperature is equal to the temperature of the compressible volume at the segment inlet. Second, for two-phase and vapor segments, it is assumed that the enthalpy along the segment is constant and is equal to the enthalpy of the compressible volume at the segment inlet.

During the transient calculation, the algorithm first solves for segment flows and compressible volume enthalpies and pressures, then invokes the enthalpy transport model to update the segment enthalpy distributions. The enthalpy transport model begins by finding the average over the timestep of the fluid velocity in each segment from the expression

(7.2-52)\[\overline{u} = \frac{w^{n + 1/2}}{\overline{\left( \rho A \right)}}\]

where

(7.2-53)\[\overline{\left( \rho A \right)} = \frac{\overline{\rho}}{L} \sum_{j} A_{j} L_{j}\]

The summation is over all the elements in the segment, with \(A_{j}\) the cross sectional area of an element, \(L_{j}\) the element length, and \(L\) the length of the segment. It is assumed that the fluid which was in the segment at the start of the timestep has all travelled a distance \(\overline{u} \Delta t\) over the timestep. The algorithm therefore shifts the enthalpy distribution by \(\overline{u} \Delta t\), plus accounts for fluid which has entered the segment inlet and fluid which has left from the segment outlet. In the case of the first timestep in the transient, this procedure results in information about the enthalpy at three points: the inlet, the outlet, and at \(\overline{u}_1 \Delta t_{1}\), the point corresponding to fluid which was at the inlet at the start of the timestep. After the second timestep, the enthalpy will be known at four points along the segment: the inlet, the outlet, at \(\overline{u}_2 \Delta t_{2}\) from the inlet, and at \(\left( \overline{u}_1 \Delta t_{1} + \overline{u}_2 \Delta t_{2} \right)\) from the inlet, assuming that this last point has not travelled so quickly as to pass out the segment outlet. The result is that the code tracks the progression of a set of points through each segment each timestep and interpolates between the points if enthalpy values are needed which fall between points (such as at the ends of the elements).

If fluid is moving fairly quickly through a segment, the number of points being tracked will remain small. However, if the flow becomes low enough, a situation could develop in which the algorithm is tracking an unnecessarily large number of points. Therefore, for each segment, a maximum is set on the number of points which can be tracked at one time, and a new point is not added at the end of a timestep if the point added most recently has not moved sufficiently far from the segment entrance.

In the vapor segments, simple enthalpy transport does not always provide an accurate model, since the enthalpy of a highly compressible fluid is sensitive to changes in pressure along the segment. Simple enthalpy transport might, for example, produce very inaccurate results during a transient in which the vapor moved slowly relative to the changes in pressure with time. Therefore, in the vapor segments, a second algorithm is available which assumes that the enthalpy along the length of a segment is constant in space and is identical to the enthalpy of the fluid in the compressible volume at the segment entrance. The user can set a flag to choose between enthalpy transport or constant enthalpy in vapor segments.

7.2.3.5. Boundary Conditions

Often, it is desirable to perform calculations on only a portion of a power plant and to use boundary conditions to simulate the effect of the remainder of the plant. The balance‑of‑plant model has two types of boundary conditions available for this purpose: a flow boundary condition and a volume boundary condition. The flow boundary condition specifies flow and enthalpy as a function of time in a special flow segment attached to a compressible volume of the user’s choice. The values of flow and enthalpy are either given by the user or are controlled by the plant control system. Multiple flow boundary conditions can be applied to the system. Flow boundary conditions are treated explicitly, and so they contribute to the combined mass and energy equations, Eq. (7.2-37) and Eq. (7.2-44), only in the term

(7.2-54)\[\Delta P = - \Delta t \sum_{j} w_{j}^{n} h_{j}^{n} \text{sgn} \left(j, l \right)\]

which is the second term in the numerator. The summation over \(j\) must include not only all flow segments which are attached to volume \(l\) but also any flow boundary condition attached to the volume.

A volume boundary condition is modelled as a compressible volume in which pressure, enthalpy, and quality as a function of time are either user‑input or controlled by the plant control system. The volume can be attached to one or more flow segments. Multiple volume boundary conditions can be designated in a network. A volume boundary condition contributes an endpoint pressure to any flow segments to which it is attached and so affects terms \(a_{1},\ a_{2}\), and \(a_{3}\) (Eq. (7.2-19), Eq. (7.2-20), Eq. (7.2-21)) in the momentum equation. It also provides inlet enthalpy and quality for any attached segments in which flow is directed out from the boundary condition.

Both flow and volume boundary conditions are updated at the start of each timestep.

7.2.4. Solution Procedure

The result of the discretization procedure described in Section 7.2.3 is a set of two equations: Eq. (7.2-17), which expresses the change in segment flow rate as a function of the changes in segment endpoint pressures, and Eq. (7.2-47), which expresses the change in compressible volume pressure as a function of the changes in the flows in each of the segments attached to the volume. These two equations can be combined into a single equation which has only changes in compressible volume pressures as variables. By substituting Eq. (7.2-17) in Eq. (7.2-47), the segment flows are eliminated, giving

(7.2-55)\[\begin{split}\Delta P = - \Delta t \bigg\{ Q_{l}^{n} + \sum_{j} w_{j}^{n} \left[ h_{j}^{n} - h_l^n + v_l^n \text{DHDN} \left( l \right) \right] \text{sgn} \left(j, l \right) \\ + \sum_{j} \text{sgn} \left(j, l \right) \left[h_{j}^{n} - h_{l}^{n} + v_{l}^{n} \text{DHDN} \left( l \right) \right] \big[a_{1} \left(J \right) + \\ \left(a_{2} \left(j \right) + \Delta t \left[ \Delta P_{in} \left(j \right) - \Delta P_{out} \left( j \right) \right] \right) \big] / \left[a_{0} \left(j \right) - a_{3} \left( j \right) \right] \bigg\}\ / \ \text{DENOM} \left(l \right)\end{split}\]

If Eq. (7.2-55) is written for all \(L\) compressible volumes in a system, the result is a set of equations, each of the form

(7.2-56)\[\sum_{J = 1}^{L} c \left(I, J \right) \Delta P_{J} = d \left( I \right)\]

The forms of the coefficients \(c \left(I, J \right)\) and the source terms \(d \left( I \right)\) in Eq. (7.2-56) are most clearly derived by separating out the contribution of each segment in Eq. (7.2-55). Consider a segment \(k\), in which fluid flows from volume \(I\) to volume \(J\). If Eq. (7.2-55) is written for volume \(I\), the contribution of segment \(k\) to Eq. (7.2-55) can be expressed as the term

(7.2-57)\[\begin{split}\Delta P_{l} \left( k \right) = -\Delta t \bigg\{ -h_{k}^{n} \left( I \right) w_{k}^{n} + w_{k}^{n} \left[ h_{I}^{n} - v_{I}^{n}\ \text{DHDN} \left( I \right) \right] \\ - \left[h_{k}^{n} \left( I \right) - h_{I}^{n} + v_{I}^{n} \text{DHDN} \left( I \right) \right] \big[a_{1} \left(k \right) + a_{2} \left(k \right) \\ + \Delta t \left[ \Delta P_{I} - \Delta P_{J} \right] / \left(a_{0} \left(k \right) - a_{3} \left(k \right) \right) \bigg\}\ / \ \text{DENOM} \left( I \right)\end{split}\]

The term \(h_{k}^{n} \left( I \right)\) is the enthalpy at the interface between segment \(k\) and volume 1. Eq. (7.2-55) can then be rewritten as

(7.2-58)\[\Delta P_{1} = -\Delta t Q_{I}^{n}\ / \ \text{DENOM} \left(I \right) + \sum_{k} \Delta P_{I} \left( k \right)\]

The signs in Eq. (7.2-58) are consistent with the convention that a positive flow out of a volume is a flow in the negative direction.

Comparing Eq. (7.2-56) and Eq. (7.2-58) shows the contributions from segment \(k\) to the coefficients \(c\left(I, \right)\) of the pressure changes to be

(7.2-59)\[c_{k}\left( I,J \right) = - {\Delta}t\left( h_{k}^{n}\left( I \right) - h_{I}^{n} + \nu_{I}^{n}\text{DHDN}\left( I \right) \right) \bullet ( - {\Delta}t)/\left\lbrack (a_{0}\left( k \right) - a_{3}(k)) \bullet \text{DENOM}(I) \right\rbrack\]

and

(7.2-60)\[c_{k} \left(J, I \right) = - c_{k} \left(I, J \right)\]

while the contribution to the source term \(d\left( I \right)\) is

(7.2-61)\[\begin{split}d_{k} \left( I \right) = - \Delta t \bigg\{ - h_{k}^{n} \left( I \right) w_{k}^{n} + w_{k}^{n} \left(h_{I}^{n} - v_{I}^{n} \text{DHDN} \left( I \right) \right) \\ - \left(h_{k}^{n} \left( I \right) - h_{I}^{n} + v_{I}^{n} \text{DHDN} \left( I \right) \right) \left(a_{1} \left( k \right) + a_{2} \left( k \right) \right) \ / \\ \left(a_{0} \left(k \right) - a_{3} \left( k \right) \right) \bigg\}\ / \ \text{DENOM} \left(I \right)\end{split}\]

and so Eq. (7.2-57) can be rewritten as

(7.2-62)\[\Delta P_{I} \left( k \right) = - \Delta P_{J} c_{k} \left(I, J \right) - \Delta P_{I} c_{k} \left(I, J \right) + d_{k} \left(I \right)\]

Eq. (7.2-62) can be substituted into Eq. (7.2-58) with the result, after rearrangement,

(7.2-63)\[\Delta P_{I} \left( 1 + \sum_{k} c_{k} \left(I, I \right) \right) + \sum_{k} \Delta P_{J\left( k \right)} c_{k} \left(I, J \right) = -\Delta t Q_{I}^{n} \ / \ \text{DENOM} \left(I \right) + \sum_{k} d_{k} \left(I \right)\]

Comparing Eq. (7.2-56) and Eq. (7.2-63) shows that the coefficients of the pressure changes have the form

(7.2-64)\[c\left(I, I \right) = 1 + \sum_{k} c_k \left(I, I \right)\]

and

(7.2-65)\[\begin{split}c\left(I, J \right) = \sum c_{k} \left(I, J \right) \\ k: J\left(k \right) = J\end{split}\]

(the range given for the sum in Eq. (7.2-65) is over all segments which run between volumes \(I\) and \(J\)), while the source term is given by

(7.2-66)\[d\left( I \right) = - \Delta t Q_{I}^{n}\ / \ \text{DENOM} \left( I \right) + \sum_{k} d_{k} \left( I \right)\]

If Eq. (7.2-56) is written for all \(L\) compressible volumes, an \(L \text{x} L\) matrix equation is created which can be inverted and solved for all \(L\) volume pressure changes simultaneously. Once the pressure changes are known, the change in mass flow rate in each segment can be computed from Eq. (7.2-17), and the changes in volume enthalpy can be calculated from the equation of state. The explicit quantities, such as density and heat source, can then be updated.

Note that this procedure constitutes a simultaneous solution for the changes in volume pressure, volume enthalpy, and segment mass flow rate, not just for the changes in pressure. The procedure simply takes advantage of two facts: 1) each flow change is a function of endpoint pressure changes only (as expressed by the momentum equation), and therefore the flow changes can be updated one at a time once the pressure changes have been computed, and 2) the coupling between the changes in enthalpy in neighboring volumes can be eliminated by using the equation of state to express the change in enthalpy as a function of the change in pressure and the changes in the attached segment flows, and so the enthalpy changes can be updated one at a time once the changes in pressure and flow rate are known. The three steps of solving a matrix equation for the changes in pressure, then updating the flows, then updating the enthalpies comprise a simultaneous solution for all three variables.

7.2.5. Coupling Between the Balance-of-Plant Model and the Steam Generator Model

It is important to note that the balance‑of‑plant model does not include the water side of the steam generator. Instead, the steam generator is modelled separately and is explicitly coupled to the balance‑of‑plant model. By so doing, the steam generator can be represented without use of the momentum equation (see Section 7.3), thereby significantly reducing the number of implicitly coupled momentum cells in the balance of plant. This is particularly important in a systems analysis code, where a fully‑implicit solution scheme can easily result in unacceptably long running times. The omission of a momentum equation in the steam generator requires the assumptions that (1) the pressure drop across the steam generator can be neglected and that (2) the coupling between the steam generator outlet and the remainder of the balance of plant is not very strong; these assumptions are valid in a wide range of operational and accident situations in nuclear power plants.

The coupling between the balance of plant and the steam generator is accomplished by having the steam generator provide a pressure at the subcooled/two‑phase interface within the steam generator and a flow from the steam generator outlet into the outlet plenum. A detailed discussion of how the steam generator model calculates the interface pressure and outlet flow is given in Section 7.3. The balance‑of‑plant model simulates the evaporator subcooled/two‑phase interface as a pseudo‑compressible volume which serves as a boundary condition volume, with the volume pressure specified by the steam generator model. The coupling is completed by having the balance‑of‑plant model provide the subcooled region flow and the average steam generator pressure. The subcooled region is treated as one of the flow segments in the balance‑of‑plant network of segments and volumes, with the steam generator model providing a region‑averaged enthalpy which is used to calculate the average liquid temperature and thermodynamic properties needed in the momentum equation. Thus, the balance‑of‑plant model can calculate the subcooled region flow at the same time that flows in the other flow segments are computed, and it can calculate the steam generator average pressure as the linear average of the pressures in the steam generator inlet and outlet plena.

The coupling between the balance‑of‑plant and steam generator models requires some time averaging to stabilize the rate of change of the steam generator pressure, as well as limits on the rate of change of the subcooled zone flow; neither constraint affects the accuracy of the overall calculation. A detailed explanation of these constraints is provided in Section 7.3.

7.2.6. Implementation of the Balance-of-Plant Model in SASSYS-1

The coding which implements the mathematical model described in the preceding sections can be divided into two main parts: a steady‑state initializer and a transient solution algorithm. The calculational procedure followed in each part will be described now, and then the operation of the coding subroutine by subroutine will be outlined.

7.2.6.1. Steady‑State Initialization

The job of the steady‑state initializer is to derive the system parameters from the data which the user has entered. The parameters to be calculated include the following:

For volumes:	the density and enthalpy are computed from the equation of state
For segments:	the length is computed from the element lengths, the endpoint enthalpies are derived from the equation of state, and the enthalpy transport arrays are set to steady-state values.
For elements:	the endpoint enthalpies are found from the equation of state, the orifice coefficient is calculated from the momentum equation, and the gravity head is computed from the average density (found from the equation of state) and the endpoint elevations
For steam generators:	the inlet enthalpy is set from the inlet plenum enthalpy, and the steam generator pressure is computed as the average of the pressures in the inlet and outlet plena
For heaters:	the heat transfer coefficients are initialized for the simple heater model; Section 7.4 discusses the initialization procedure for all other types of heaters. In all cases, the heat source term steady state value is computed
For pumps:	the pump head is computed from the pump element endpoint pressures, and the corresponding pump speed is then determined through an iterative procedure identical to that used for the sodium-side pumps (see Chapter 5)

7.2.6.2. The Transient Solution Algorithm

This algorithm solves the difference equations described earlier at each timestep. The timestep size used is based on the size of the timestep used in the sodium‑side calculations by the PRIMAR subroutine. A maximum value for the balance‑of‑plant timestep is defined as a user‑specified fraction of the PRIMAR timestep, with the balance‑of‑plant timestep always less than or equal to the PRIMAR timestep. However, the balance‑of‑plant timestep is also limited by the rates of change of the segment flows and the compressible volume pressures, as well as being limited by rates of change of the steam generator water and sodium flows, metal and sodium temperatures, water enthalpies, waterside void fractions, and waterside heat transfer coefficients. Therefore, depending upon transient conditions, the balance of plant may operate on a significantly smaller timestep than does the sodium loop. The balance of plant and the steam generator models always operate on the same timestep.

The calculation proceeds as follows:

1. For each steam generator, the feedwater enthalpy and flow and average pressure calculated by the balance-of-plant model the previous step are passed to the steam generator algorithm. If a superheater is associated with a steam generator, the superheater model algorithm is called first, then the steam generator model algorithm is used.

2. The steam generator outlet flow and enthalpy and the pressure difference between the subcooled/two-phase interface and the evaporator outlet are transferred to the balance-of-plant coding for each steam generator. For all superheaters, the superheater outlet enthalpy, average temperature, and average density are passed to the balance-of-plant model.

3. Now, the coefficients \(c \left( I, J \right)\) and source terms \(d \left( I \right)\) of Eq. (7.2-56) must be calculated. The first step is to compute the terms which depend only on conditions within a compressible volume and do not involve data from the segments. Primarily, this means computing the terms DHDN and DENOM in Eq. (7.2-45) and Eq. (7.2-46).

4. Next, the momentum equation coefficients \(a_{0}\) through \(a_{3}\) must be found for each segment (see Eq. (7.2-18) through Eq. (7.2-21)).

5. The terms \(c \left( I, J \right)\) and \(d\left( I \right)\) can now be assembled by traversing the nodalization segment by segment and using Eq. (7.2-64) through Eq. (7.2-66). The contributions from any flow boundary conditions, given by Eq. (7.2-54), are also included at this time.

6. The matrix equation resulting from step 5 is now solved for the compressible volume pressure changes by using Gauss‑Jordan elimination.

7. Now that the changes in the volume pressures over the timestep are known, the updated pressures can be computed, and the updated segment flows can be found from Eq. (7.2-17).

8. The heat source terms for any heaters other than those represented by the simple model are updated now.

9. The new segment flows are used to update the compressible volume densities from Eq. (7.2-31). The changes in the compressible volume enthalpies can be computed from the changes in volume pressures and segment flows using Eq. (7.2-35) for single‑phase volumes and Eq. (7.2-43) for two‑phase volumes.

10. The enthalpy transport model is now used to calculate the current enthalpy distribution along each segment, except in segments where the user has opted for a uniform enthalpy distribution instead of enthalpy transport.

11. The new pump heads and speeds and the new gravity heads are now calculated. The heater source terms of any heaters represented by the simple heater model are also updated.

7.2.6.3. Code Operation

The calculational procedures just described are implemented by the set of subroutines and functions listed in Table 7.2.1, which includes both a brief description of the usage of each subroutine and identifies the calling subroutine except in the case of material property functions which are called from a number of different subroutines. The structure of the coding made up of these subroutines and functions is diagrammed in Figure 7.2.1 and Figure 7.2.2. The operation of this coding will now be discussed in some detail.

The progression of the calculation through the steady state initialization is diagrammed in Figure 7.2.1. The calculational sequence moves from left to right and from top to bottom in the diagram. Subroutine SSPRM4 is an initialization subroutine used by the sodium‑side PRIMAR‑4 module which has been modified to call the initialization subroutines for the balance‑of‑plant module also. SSPRM4 begins by calling RENUM, which reads the balance‑of‑plant input information and rearranges the nodalization to the form that the code will actually use (see Section 7.2.7.1). For volumes for which pressures and temperatures are centered as input data, RENUM also computes the volume enthalpies, and for this task it needs function FINDH. This function uses a Newton-Raphson scheme to solve an equation-of-state for enthalpy as a function of temperature and pressure. FINDH is also used by a number of subroutines in the transient calculation. When RENUM stores information concerning the evaporator model, it uses subroutines LoadSG and StoreSG to find the correct storage locations for each evaporator; similarly, when RENUM handles superheater information, it uses LoadSH and StoreSH to store the data correctly for each superheater. The relief valve initializing routine SSRVW is also called from RENUM, as are subroutines SELSRT, which orders members of each component category from smallest to largest user number (this is done in case the user numbering is not consecutive), and PRNTST, which sets flags to invoke prints of just the parameters selected by the user for printing.

Table 7.2.1 Descriptions of the Balance‑of‑Plant Subroutines

Routine	Description
ARF	This subroutine is used to solve the transcendental equation needed to find heater water level in heaters which are right-circular cylinders oriented so the cylinder axis is parallel to the ground. It is called from WTRDRV.
BOP_UpdateSG	This subroutine updates beginning of timestep variables in the evaporator model. It is called from INIT in the steady-state and from SGUNIT in the transient.
BOP_UpdateSH	This subroutine updates beginning of timestep variables in the superheater model. It is called from INITS in the steady-state and from SHUNIT in the transient.
CHVLW	This subroutine implements the check valve model. It tests to see whether a check valve has met the criteria for closing (if the valve is open) or opening (if the valve is closed) and sets the value of the orifice coefficient G2PW correctly before passing control to PIFLSG to compute the contribution of the valve to the segment moment equation. It is called from WTRDRV.
DTLM	This function performs the log mean temperature difference calculation when the single‑node version of the steam generator model is used. It is called from INIT and SGUNIT.
FINDH	Function FINDH solves the equation of state for enthalpy as a function of temperature and pressure by using a Newton‑Raphson scheme. This procedure is necessary because no correlation for enthalpy as a function of temperature and pressure is provided in the set of material properties expressions used in SASSYS.
HFlFUN	This function computes saturated liquid water enthalpy.
HGlFUN	This function computes saturated steam enthalpy.
INIT	This subroutine initializes the evaporator of the steam generator model. It is called from SSSTGN.
INITS	The superheater is initialized in this subroutine. It is called from subroutine SSSTGN.
LoadSG	The variables used in the steam generator model are not subscripted to accommodate more than one steam generator. Therefore, the data for each steam generator are stored in a single array and are transferred in and out as the calculation proceeds from steam generator to steam generator. LoadSG loads data into the associated steam generator common blocks; StoreSG stores common block data into the steam generator data structures. It is called from RENUM and from INIT in the steady state and from TSBOP in the transient. The subroutine which performs this transfer for the superheater variables is LoadSH.
LoadSH	This subroutine operates just as LoadSG does, but it transfers variables for the superheater model rather than the evaporator model. It is called from RENUM and INITS in the steady state and from TSBOP in the transient.
NAHT	The sodium heat transfer coefficient for a node within the evaporator is computed in this routine. It is called from INIT in the steady state and from SGUNIT in the transient.
NAHTS	The sodium heat transfer coefficient for a node within the superheater is computed in this routine. It is called from INITS in the steady state and from SHUNIT in the transient.
PIFLSG	This is the subroutine which computes the contribution made to the momentum equation by a pipe element. It is called from WTRDRV.
PLTBOP	This subroutine saves balance‑of‑plant data each main timestep for plotting. It is called in the steady state from SSBOP and in the transient from TSBOP.
PMPFLW	PMPFLW calculates the contribution made by a pump element to the momentum equation of the segment in which the pump is located. It is called by WTRDRV.
PMPFNW	This subroutine updates the speeds and heads of all pumps on the balance-of-plant side once the updated segment flows have been determined. It is called from WTRDRV.
PRNTST	This subroutine sets print flags so that only the parameters selected by the user for printing will be printed by subroutine WTRPRT. It is called from RENUM.
PRSH2O	PRSH2O is called only in the steady state and calculates the orifice coefficient and initial pressure drop for each element except for pumps, for which the orifice coefficient is defined to be zero. It is called from SSBOP.
RENUM	This subroutine reads the fixed‑point balance‑of‑plant data, generates the nodalization which the code will use internally, and reads the floating‑point data. It is called in the steady state from SSPRM4.
REVLW	This subroutine computes the fractional valve opening area as a function of pressure drop for a relief valve. A simple hysteresis curve is used to represent the opening area, so that the valve does not chatter when the pressure drop is near the point at which the valve opens or closes. The relief valve is modeled to open and close with a response time, which is the maximum valve opening time, to avoid numerical instabilities caused by the step changes in flow. It is called from TSRVW.
SELSRT	This subroutine orders the members of each component category by user number, from smallest to largest; this allows the code to handle cases in which the user has not used consecutive numbers for members of one or more component categories. It is called from RENUM.
SFFUNW	This function computes saturated liquid water entropy.
SGFUNW	This function computes saturated steam entropy.
SGMOM	This is the subroutine which calculates the momentum equation terms for the subcooled region in the evaporator and for the superheater. It is called from WTRDRV.
SGUNIT	SGUNIT is the subroutine which computes temperatures and flows in the steam generator. It is also the subroutine which feeds information from the steam generator model to the balance‑of‑plant model. It is called from TSBOP.
SHUNIT	Temperatures along the superheater are computed by this routine. It is called from WTRDRV.
SSBOP	This subroutine does the steady‑state initialization for the balance‑of-plant model. It is called from SSPRM4.
SSCFUN	This function calculates the subcooled water entropy as a function of pressure and enthalpy.
SSHFUN	This function calculates the superheated steam entropy as a function of pressure and enthalpy.
SSHTRW	Most of the initialization of any heaters is done in SSHTRW. SSHTRW computes the shell‑side temperatures and/or the tube‑side temperature distribution (along with the surface heat transfer area calibration factor). The heater heat source terms (and the heat source terms in the drain and/or the desuperheating region, if such regions are present) are calculated also in this subroutine. In addition, SSHTRW checks mass and energy conservation and finds the pseudo‑heat conduction coefficient. It is called from SSBOP.
SSNZZL	This subroutine performs the steady‑state initialization for the nozzle model. SSNZZL computes the isentropic enthalpy and the fluid density following the isentropic expansion. The steady‑state nozzle velocity is calculated, and the nozzle flow area is calibrated in this subroutine. It is called from SSBOP.
SSPMPW	The steady‑state initialization of the pumps in the balance of plant is done in SSPMPW. It is called from SSBOP.
SSPRM4	SSPRM4 is a PRIMAR‑4 subroutine which is also used to call the steady state subroutines RENUM and SSBOP which initialize the balance‑of‑plant model. It is called from PRIMAR‑4 driver subroutine SSTHRM.
SSRVW	This subroutine calibrates the relief valve flow area for a fully open valve according to the relief valve capacity. This is done in the steady‑state balance‑of‑plant, when the flow through the relief valve is normally zero. It is called from RENUM.
SSTRBN	The steady‑state initialization of the turbine stage is done in this subroutine. SSTRBN checks the conservation of mass and energy in the turbine stage. It also computes the turbine torque and sets the generator torque. It is called from SSBOP.
StoreSG	The variables used in the steam generator model are not subscripted to accommodate more than one steam generator. Therefore, the data for each steam generator are stored in a single array and are transferred in and out as the calculation proceeds from steam generator to steam generator. StoreSG stores common block data in the steam generator data structures, whereas LoadSG is utilized to load data into common. It is called from RENUM and from INIT in the steady-state and from TSBOP in the transient. The subroutine which performs this transfer for the superheater variables is StoreSH.
StoreSH	This subroutine operates just as StoreSG does, but it transfers variables for the superheater model rather than the evaporator model. It is called from RENUM and INITS in the steady-state and from TSBOP in the transient.
TRNSPT	TRNSPT tracks the transport of enthalpy through each segment in the balance of plant. It is called from subroutine WTRDRV.
TSBOP	This is the driver subroutine which calls the steam generator model and the balance‑of‑plant model. It also saves waterside plot data and calls WTRPRT to print waterside output. It is called from TSSTGN.
TSHTRW	The transient calculation of heater temperatures and heat source are done in TSHTRW. This subroutine updates the heater shell‑side temperature and/or the tube‑side temperature distribution. The heater heat source terms (and the heat source terms in the drain and/or desuperheating regions, if such regions are present) are also updated in TSHTRW. It is called from WTRDRV.
TSNZZL	The transient calculation of the nozzle velocity, the isentropic fluid enthalpy, the fluid density following the isentropic expansion, and the flow rate is done in this subroutine. It also generates the coefficients of the nozzle momentum equation for the matrix elements. It is called from WTRDRV.
TSRVW	This subroutine calls REVLW to check if the relief valve is open or not. It the relief valve is open, TSRVW generates the coefficients of the relief valve momentum equation for the matrix elements and later is called again from WTRDRV to calculate the flow rate; otherwise TSRVW is bypassed and returned to the calling subroutine WTRDRV.
TSTRBN	This subroutine updates the turbine stage parameters in the transient. TSTRBN calculates the turbine stage work term, updates the turbine torque, and adjusts the rotor angular velocity. It is called from WTRDRV.
VALVEW	The orifice coefficient used for a standard valve is computed in this subroutine. It is called from TSBOP.
WTRDRV	WTRDRV is the transient driver for the balance‑of‑plant calculation. It is in WTRDRV that the updated balance‑of‑plant parameters are computed. It is called from TSBOP.
WTRPRT	This subroutine prints the current values for the balance‑of‑plant parameters. The frequency with which it is called is at the user’s discretion. It is called from TSBOP.

Figure 7.2.1 Balance of Plant Steady-State Program Structure

Figure 7.2.2 Balance of Plant Transient Program Structure (TSBOP)

Once RENUM completes its work, SSPRM4 moves on to call SSBOP to do the remainder of the steady‑state balance‑of‑plant initialization. This is the subroutine in which the steady‑state enthalpies, gravity heads, segment lengths, etc. are computed. All the calculations necessary to complete the steady‑state initialization of the balance of plant are performed in SSBOP except the initialization of the nozzles, which is done in SSNZZL; the initialization of the turbine, which is done in SSTRBN; the initialization of the heaters, which is done in SSHTRW; the calculation of the element orifice coefficients, which is done in PRSH2O, and the calculation of the pump speed and torque, which is performed in SSPMPW. Finally, SSBOP calls PLTBOP to save steady‑state data for plotting.

After the balance of plant has been initialized, SSPRM4 calls SSSCLP, a sodium‑side subroutine which in turn calls another sodium‑side routine, SSLQSG, which then calls SSSTGN, the steam generator initialization driver. Both the superheater and evaporator models are initialized from this subroutine with calls to INITS and INIT, respectively. Section 7.3 discusses these routines in detail.

With the steady‑state initialization completed, the transient calculation can begin. Figure 7.2.2 outlines the progression of the calculation through the coding. The PRIMAR‑4 subroutine STEPTM calls subroutine TSBOP, which is the driver for the waterside transient calculation. After updating several parameters to the current sodium‑side timestep, TSBOP calls VALVEW to update the condition of all standard valves. The code then begins to operate on the balance‑of‑plant/steam generator timestep. First, subroutine TSSTGN, the steam generator transient driver, is called. If there are any superheaters in the problem, TSSTGN calls SHUNIT to perform the heat transfer calculation within each superheater. Similarly, if there are any evaporators or once-through steam generators, TSSTGN calls SGUNIT for each one, then updates the parameters which constitute the evaporator/balance‑of‑plant interface. Both SHUNIT and SGUNIT are discussed in detail in Section 7.3.

The next step for TSBOP is to call WTRDRV, the balance‑of‑plant driver, to compute the balance‑of‑plant parameters. WTRDRV has the job of assembling the matrix equation for the compressible volume pressure changes, solving for the pressure changes, and then solving for the remaining balance‑of‑plant parameters. While most of this work is performed in WTRDRV itself, there are a number of subroutines which contribute to the calculation, as can be seen in Figure 7.2.2. The momentum equation coefficients for incompressible flow elements are computed by SGMOM for superheaters and for the subcooled region of each evaporator; by PIFLSG for pipes; by CHVLW for check valves; and by PMPFLW for pumps. For compressible flow elements, the momentum equation contributions are computed by TSNZZL for nozzles and by TSRVW for relief valves. Most calculations related to heaters other than those simulated by the simple heater model are performed by TSHTRW; simple heater model calculations take place in WTRDRV. Enthalpy transport is done by a call to TKNSPT, and PMPFNW updates pump heads and speeds. Subroutine ARF is called in conjunction with finding the new water level in some types of heaters.

Once the balance‑of‑plant calculations for a timestep are completed, TSBOP checks to see if the end of a sodium‑side PRIMAR timestep has been reached. If so, TSBOP calls PLTBOP to save plot data and calls WTRPRT to provide a printout of the waterside parameters. Both PLTBOP and WTRPRT can be called less frequently than once each PRIMAR timestep by setting the frequency of each call through input. If the end of a PRIMAR timestep has not been reached, TSBOP increments the balance‑of‑plant/steam generator timestep and begins another series of calls to TSSTGN and WTRDRV.

7.2.6.4. Data Input

The input data variable names are defined in Section 7.7.1, which also lists many of the balance‑of‑plant variables that do not represent input quantities. A complete line‑by‑line description of the input data is presented in Appendix 2.2.

7.2.7. Creating a Plant Nodalization

The first step in analyzing a particular power plant using the models discussed above is to discretize the plant layout into a network composed of the component models available in SASSYS. The elements of the network (volumes, segments, etc.) must be assigned numbers for use by the code, and there are a few simple rules governing how the numbering is done, as discussed below in Section 7.2.7.1. There are also several features of the code which can help simplify the input data required and reduce the size of the problem; these are described in Section 7.2.7.2 through 7.2.7.4.

7.2.7.1. Rules About Numbering Plant Components

Designing a nodalization for a plant layout involves going through the layout and deciding how best to simulate the plant using the component models available in the code. The plant is thereby reduced to a network of compressible volumes and flow segments, with the segments further divided into flow elements.

Once this network has been created, the nodalization is completed by numbering the volumes, segments and elements. The process of numbering is easy, as there are very few rules which must be followed in order to assemble a nodalization which SASSYS will accept. The balance‑of‑plant coding was designed to minimize numbering restrictions, primarily to make it easier for the user to add on to an existing nodalization. The current coding requires only that the user assign numbers in the following ranges:

For compressible volumes ‑‑ between 1 and 100

For segments ‑‑ between 1 and 100

For elements ‑‑ between 1 and 200

For pumps ‑‑ between 1 and 10

For volume boundary condition tables ‑‑ between 1 and 10

For flow boundary condition tables ‑‑ between 1 and 10

For standard valves ‑‑ between 1 and 40

For check valves ‑‑ between 1 and 40

For supersegments ‑‑ between 1 and 10

For heaters ‑‑ between 1 and 20

For legs of the balance of plant ‑‑ between 1 and 10

Steam generators and superheaters must be numbered consecutively beginning with 1 in order to be consistent with the sodium side coding. All members of a category (e.g., all segments) must be assigned unique numbers, but the same number may be used in more than one category (so there can be a segment 6 and an element 6, for example). The numbers used do not have to be consecutive, which makes it easy to add elements within a segment or add new volumes and segments to the entire system. An existing nodalization can be expanded with no renumbering of any item in the original nodalization. Members of a particular category may be assigned any numbers convenient for the user; there is no need to assign the number 1 to some category member.

This very flexible way of handling the nodalization is made possible by a section of the code which performs a renodalization internally once all the data concerning the nodalization set up by the user have been read. The user never sees the internal nodalization; when data are printed out or saved for plotting, they are numbered according to the user’s nodalization. However, all the calculations performed by the code are done with the internal nodalization. The code simply renumbers the members of each category according to the order in which information was entered in the data deck (for example, if the user enters data for segment 8 first, then volume 3, then volume 15, then segment 4, the code will assign segment 8 the number 1, segment 4 the number 2, volume 3 the number 1, and volume 15 the number 2). The only exception to this is the elements; the code goes segment by segment (following the internal nodalization segment numbers) and renumbers the elements consecutively within each segment. Ordering the elements consecutively within a segment allows the program to operate more efficiently.

The following discussion will give a description of how subroutine RENUM manipulates the fixed-point input data to create a new nodalization in which each type of component is consecutively numbered starting at number one. There is also extensive documentation of this process within RENUM in the form of comment cards, and anyone with a need to understand this section of the coding in detail should refer to these comment cards.

Once all the fixed-point data are read in, and before any floating-point data are entered, RENUM performs the renodalization. Part of the renodalization process is the creation of arrays which translate between the user’s numbering scheme and the scheme resulting from the renodalization. The floating-point data are not entered until after these translator arrays are created so that all floating-point arrays can be automatically ordered according to the renodalization numbering scheme as the data are read from the input file.

The goal of the renodalization is to renumber all components so that the calculations performed in solving the mass, momentum, and energy equations can be executed as efficiently as possible. If the problem is not divided into two or more legs, components of each type are simply numbered in the order in which they were entered in the fixed-point data block (so that, for example, the first element entered becomes element 1, the first volume entered becomes volume 1, etc.). If the problem is divided into two or more legs, components of each type are grouped by leg, with all components of a given type numbered consecutively within a leg in the order in which they were read in the fixed-point data block. The user must specify the order in which legs are to be arranged through the variable LEGORD.

As the fixed-point data are entered, RENUM keeps count of the total number entered of each component type. The first renodalization task it performs is to add the subcooled region of each steam generator to the total number of flow segments which were read in through input. The code then turns to the compressible volume fixed-point data. These are stored in a temporary array at the time the data are read. RENUM now marches through volume by volume, separating volume boundary conditions from the rest and initializing boundary condition variables both for volumes which are volume boundary conditions and volumes which are attached to flow boundary condition segments. The fixed-point volume data are stored in the correct permanent arrays in the order in which the volumes were read in.

The legs of the loop are now renumbered beginning at one in the order specified by the user in array LEGORD. The array LEGBCK, which translates the user’s number for a particular leg into the number assigned by the code, is generated; LEGORD is the translator array from the code numbering to the user’s numbering. Once the legs are reordered, the compressible volumes (excluding volume boundary conditions) can be renumbered so that the volumes in leg 1 are numbered consecutively beginning with the number one, in the order in which they were entered in the fixed-point data input; the volumes in leg 2 are ordered consecutively following those in leg 1, etc. The arrays NCVIN and NCVOUT, which mark the first and last volumes in each leg, are set at this time, and the arrays NCVBCK, which translates from the user’s numbering of volumes to the code’s numbering, and NCVTRN, which translates from the code’s numbering to the user’s numbering, are both rearranged to be consistent with the renumbering of the volumes by leg. The remaining fixed-point volume input arrays, NTPCVW, NCVBCW, NLGCVW, and NQFLG are also rearranged.

At this point, the code turns to the flow boundary conditions and to the outlet flows passed by the evaporator model to the balance-of-plant coding. The flow boundary condition segments are numbered consecutively leg by leg, and the array JCVW, which specifies the numbers of the compressible volumes at the segment endpoints, is set for each boundary condition segment. The arrays ISGIN and ISGOUT, which designate the first and last boundary condition segments in each leg, are also set at this time. This entire process is then repeated for the segments representing each evaporator outlet flow.

The boundary condition volumes and the evaporator subcooled/two-phase interfaces are next. The code treats the interfaces as additional boundary condition volumes, with the evaporator model providing the thermodynamic parameters at each interface. RENUM first numbers the boundary condition volumes consecutively, with the numbers beginning immediately after the remaining volumes, then numbers the subcooled/two-phase interface in each evaporator in the order of numbering of the evaporators. The total number of volumes in the problem, then, is the sum of the number of interior volumes, plus the number (if any) of boundary condition volumes, plus the number of evaporator subcooled/two-phase interfaces.

After testing to see that the total numbers of volumes, segments, elements, and pumps do not exceed the dimensions of the arrays associated with these components, the code reorders several fixed-point arrays of volume-related parameters, including JCVW, NLGCVW, NBCCVF, NBCCVP, and ICVSGN. JCVW is also set for the evaporator outlet flow segments at this point. RENUM then moves on to renumbering the segments, grouping them by leg as was done for the volumes. ISGIN and ISGOUT are set here, too, to flag the first and last segment in each leg. Once the segments are renumbered, the code revises all fixed-point segment-related arrays (such as NODMAX, the maximum number of enthalpy transport nodes allowed in a segment) so that these arrays reflect the revised segment numbering rather than the user’s original numbering. The elements can now be renumbered, and this is done segment by segment, with elements numbered consecutively within a segment.

The final step in creating the revised nodalization is to generate for each volume the arrays NSEGCV, ISEGCV, and ISGNCV, which give, respectively, the number of segments attached to the volume, the numbers of those segments, and the direction of flow in each attached segment. RENUM then proceeds to read in the balance-of-plant floating-point data.

7.2.7.2. Supersegments

Frequently, the best way to initialize regions containing superheated vapor is to assume that the enthalpy is constant throughout the region. However, the input data available are usually in terms of pressures and temperatures, not enthalpy, and so setting the enthalpy constant in all the volumes and segments making up a region can require some extra calculation on the part of the user and can also result in some input data inconsistencies if the user does not have available the same equation‑of‑state functions as are used by the code. This difficulty is easily resolved by making use of an input device called a supersegment. A supersegment is a chain of compressible volumes and flow segments, beginning and ending with a volume. The code sets the steady‑state enthalpy throughout the chain, up to but not including the terminating volume, to the value of the enthalpy in the volume at the entrance to the supersegment. Up to ten supersegments can be assigned to a nodalization, and a volume can be the terminus of more than one supersegment. Supersegments provide an option which can simplify input data preparation for the user.

7.2.7.3. Legs of the Nodalization

A leg of the nodalization is the set of all volumes and segments contained between two boundary conditions on the water side. A boundary condition in this case can be a flow or volume boundary condition, or it can be an interface between a balance‑of‑plant component and the steam generator. Any nodalization of a plant can be considered a single leg, but in some cases, it is possible to break the plant up into more than one leg. This has the advantage of reducing the dimension of the matrix equations which must be solved for the changes in volume pressures (i.e., two or more smaller matrix equations are solved rather than one large one). Such a reduction can be very important if the code is run on a scalar machine; because the code vectorizes well, reducing the size of the matrix is of much less importance if a vector machine is used.

As an example of how to divide a problem into more than one leg, consider a case in which the balance of plant is modelled as beginning at a volume boundary condition, proceeding through a series of pumps, heaters, pipes, and valves up to a steam generator, then finishing past the steam generator with more piping ending in another volume boundary condition. This problem can be split into two legs: one from the inlet volume boundary condition to the subcooled/two‑phase interface inside the steam generator, and one from the steam generator outlet plenum to the outlet volume boundary condition. Modelling the problem as two legs instead of one involves slightly more fixed-point input data but may result in significant savings in running time. A decision to try to divide a problem into multiple legs should be based on whether or not the added complexity in the nodalization is justified by any savings in running time; this will depend in part upon the machine being used. For some large problems being run on scalar machines, breaking the problem into legs may be the only cost‑effective way to run a transient.

7.2.7.4. Multiplicity

Sometimes, the size of a plant nodalization can be reduced by taking advantage of symmetries which exist at least for some types of transients. The SASSYS code is equipped to take advantage of symmetries by use of a parameter called multiplicity. The operation of multiplicity in the code is best explained by a simple example.

Suppose a plant has two pumps operating in parallel, as in Figure 7.2.3. Now, some types of problems, the two pumps may behave very differently (e.g., one pump may trip and coast down while the other continues to operate), and so the momentum equation must be solved separately within each segment. However, in other problems, the pumps may operate identically, and so it would be a duplication of effort to solve the momentum equation in each segment. This is where multiplicity comes in. The two pump segments can be replaced by one segment so long as a proper accounting of the flows at the pump header and manifold is done. In this case, the correct flow contribution to each compressible volume is made by defining a multiplicity factor of two and multiplying the segment flow by this factor when solving the conservation equations. A multiplicity factor is needed at each end of any segment, since, in general, duplicate branches of a system can contain more than one segment, and so a factor of two might be needed at one end of a segment while a factor of one might be needed at the other end.

The real value of using multiplicity comes not in a simple case, such as the pump configuration of this example, but in cases involving major branches of the balance of plant. Computing time can be reduced significantly, for instance, in the case of a plant which has two steam generators and therefore two identical branches from the feedwater pump manifold to the high‑pressure turbine. In some transients, these two branches will operate identically, and so the use of multiplicity can cut the computing time nearly in half. The use of multiplicity is optional, but it is usually worthwhile to see if a particular transient can benefit from the use of multiplicity and to reconfigure the plant (and therefore the nodalization) so as to eliminate duplicate branches.

Remember, one branch is a duplicate of another only if both have the same physical configuration and they can be expected to operate identically throughout the transient. Only then can multiplicity be applied.

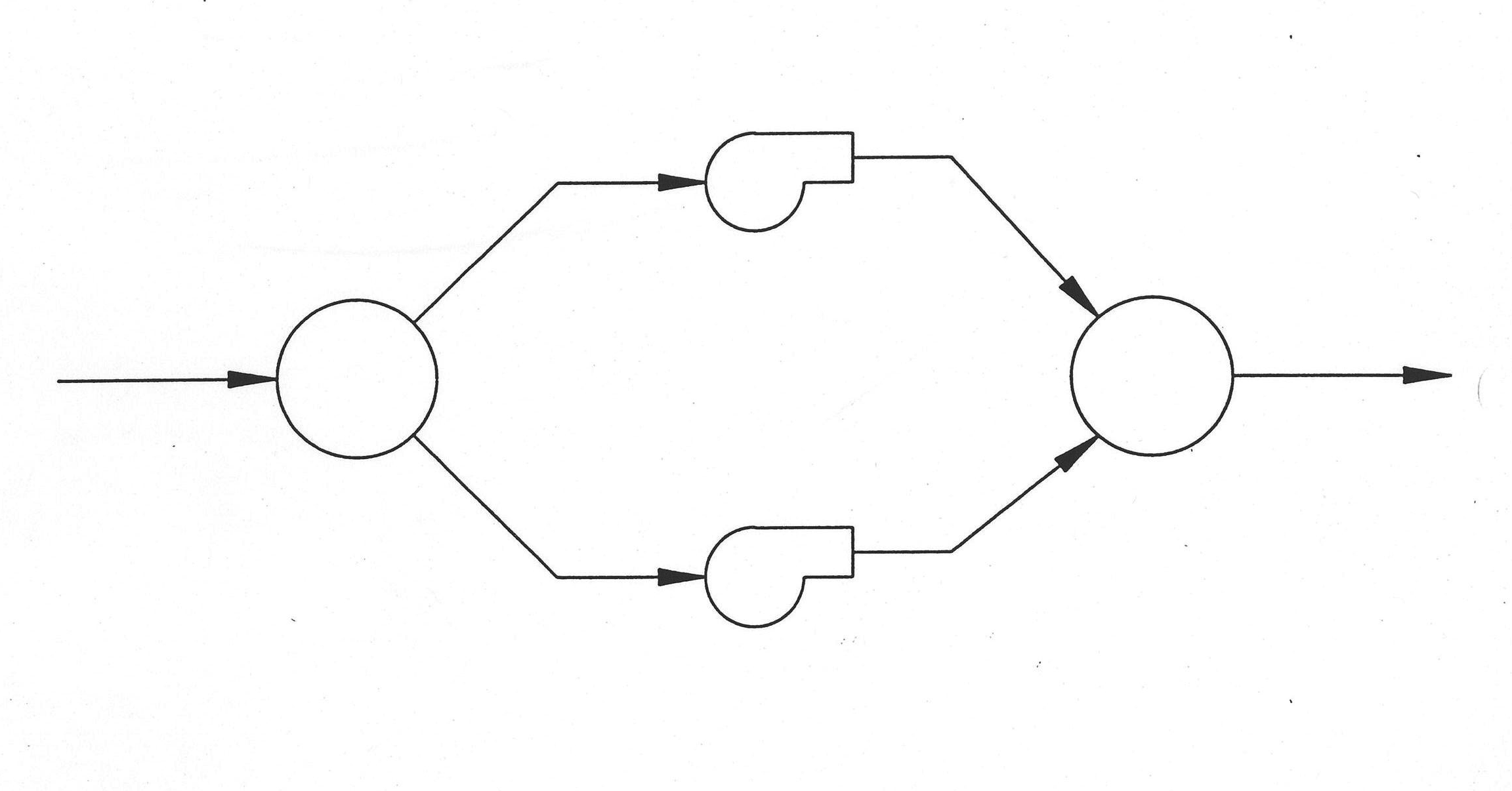
Figure 7.2.3 Exampled Problem for Demonstrating Multiplicity