7.4. Component Models
Models of power plant heat transfer components, turbine, and relief valve have been implemented in the SASSYS-1 balance‑of‑plant network model. These models extend the scope of the existing balance‑of‑plant model in the SASSYS‑1 LMFBR systems analysis code to handle nonadiabatic conditions and two‑phase conditions along flow paths, and to account for work done across the boundaries of compressible volumes. Simple conservation balances and extensive component data in the form of correlations constitute the basis of the various types of components reported here.
This work is part of a continuing effort in plant network simulation based on general mathematical models. The models described in this section are integrated into the existing solution scheme of the balance‑of‑plant coding. While the mass and momentum equations remain the same as in Section 7.2 (except for the nozzle, which has different momentum equations), the energy equation now contains a heat source term due to energy transfer across the flow boundary or to work done through a shaft. The heat source term is treated fully explicitly. To handle two‑phase conditions, the equation of state is expressed differently in terms of the quality and separate intensive properties of each phase.
Table 7.4.1 lists the various types of component models reported. The models are simple enough to run quickly, yet include sufficient detail of dominant plant component characteristics to provide reasonable results. All heater models have been tested as standalone models except the steam drum, which has been tested as part of a recirculation loop. Also an integrated plant test problem simulating an entire LMR plant was carried out with some of the heater models incorporated, and then the turbine model and the relief valve model were included and tested in similar but separate integrated test problems.
7.4.1. General Assumptions
For the simplicity of the models and for the convenience of modeling the components, certain common assumptions are made in all of the heater models. Additional assumptions necessary for each heater model will be described wherever appropriate. Assumptions for the turbine and relief valve models are given in the sections containing the discussions of these models.
The following assumptions are made in all eight heater models. Flow is incompressible on both shell and tube sides. Any two‑phase fluid entering on the shell side instantaneously separates into liquid and vapor, and a new thermal equilibrium is reached immediately. The two‑phase interface on the shell side serves as the reference point for the saturation pressure of the heater. The two phases are at a common saturation temperature, and each phase is assumed to be at a uniform enthalpy. The momentum equation governing flow entering and exiting the shell side accounts for elevation pressure differences as gravity heads. Nevertheless, intensive properties such as specific volume and thermophysical properties such as viscosity are taken to be uniform for each phase, neglecting elevation effects, when considering heat transfer coefficients.
Heaters: |
Deaerator, steam drum, condenser, reheater, flashed heater, drain cooler, desuperheating heater, desuperheater/drain cooler |
Rotating Machinery: |
Turbine (including nozzle) |
Valve: |
Relief Valve |
Additional assumptions are made for the heaters containing tube bundles. Phase change does not occur within the tube bundle irrespective of the fluid temperature on the shell side. Although two‑phase fluid may flow through pipes between two volumes, it is not allowed to be present inside the tube bundle which is the tube side of a heater. In general, the tube bundle is modeled as a single tube. Mass flux and pressure drop in the single tube of the model are the same as in the actual tube bundle, and the mass of the metal tubing is also conserved. These constraints do not allow tube length or surface area to be conserved, and so the tube surface heat transfer area is corrected to simulate the bundle heat transfer area through the use of calibration factors which provide an effective thermal resistance for conduction heat transfer.
Details of each heater will now be described, beginning with the simplest model, the deaerator, and progressing to the more complex models. The turbine and relief valve models then follow to yield a total of ten models discussed in this section.
7.4.2. Deaerator
There are two categories of heaters: open heaters and closed heaters. A deaerator is an open heater which refers to the fact that there is no distinction between tube and shell sides, so that hot fluid and cold fluid entering the heater mix together. Actually, a deaerator consists of a closed volume containing liquid and vapor at saturation conditions and is used to remove dissolved gases from an incoming fluid.
7.4.2.1. Model Description
As shown in Figure 7.4.1, a deaerator is a right circular cylinder standing on end. Due to the existence of the two‑phase interface, an appropriate response has to be implemented if the interface rises to the level of a pipe through which fluid enters or exits the heater. In the situation when fluid enters the heater, the calculation will be stopped when the interface rises to the flow opening if the incoming fluid is other than either saturated or subcooled liquid. On the other hand, if fluid flows out of the heater through the pipe, a special treatment is required as follows. Normally, each flow opening is located entirely within either the liquid or the vapor region, with outgoing fluid quality equal to 0 or 1, respectively. However, the two‑phase interface may also intersect an opening, causing two‑phase fluid to flow out of the heater. Under these circumstances, the model assumes a slip ratio of one for the two‑phase fluid and uses area weighting to compute the quality of the exiting fluid.
Consider the shaded area in Figure 7.4.2 as the area occupied by vapor exiting the pipe. Then the ratio of this shaded area to the entire opening is simply the void fraction of the exiting flow, i.e., α≡Ag/A
Slip ratio is defined as
which reduces to α=β when ug=uf (slip ratio = 1).
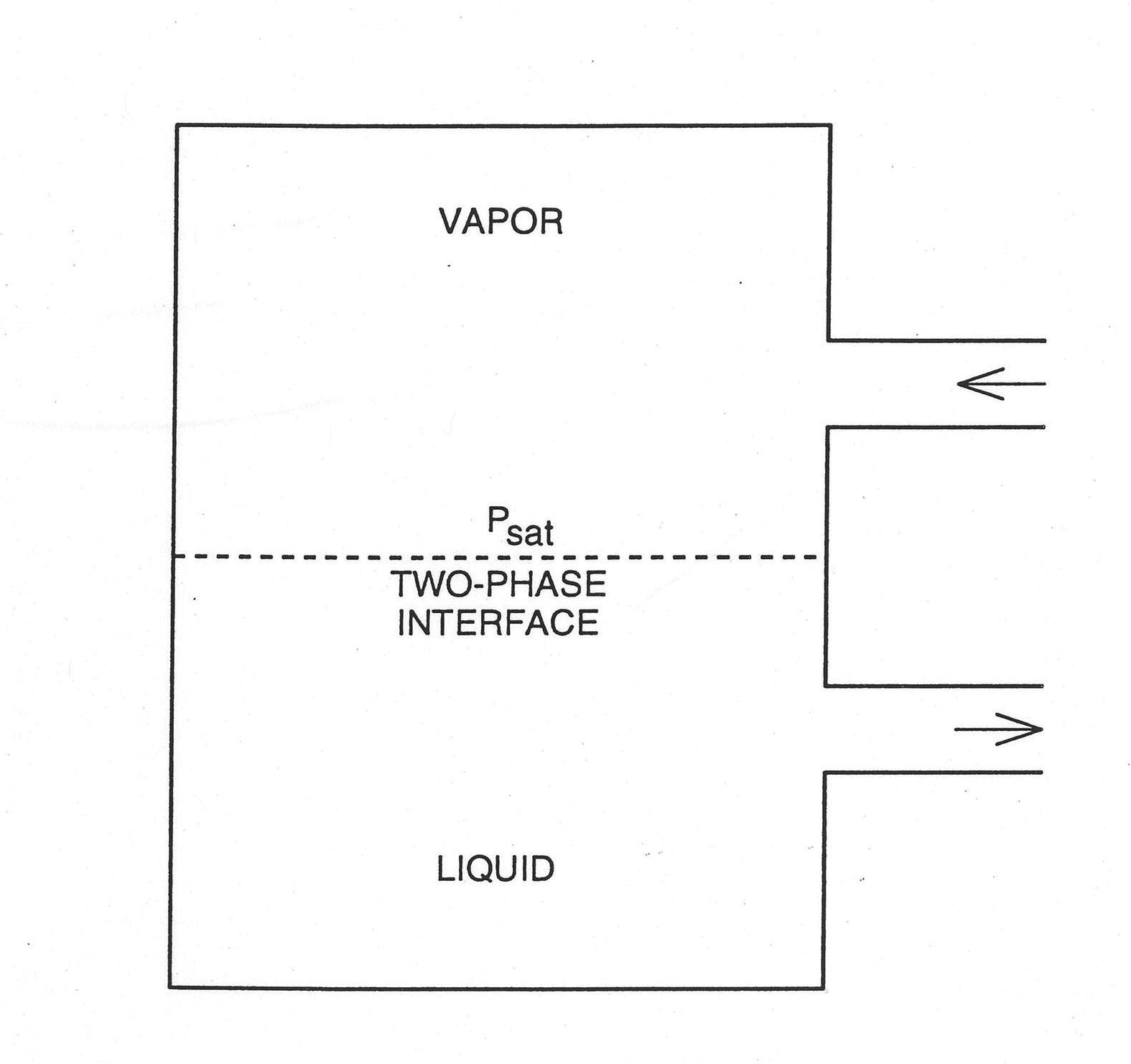
Figure 7.4.1 Deaerator
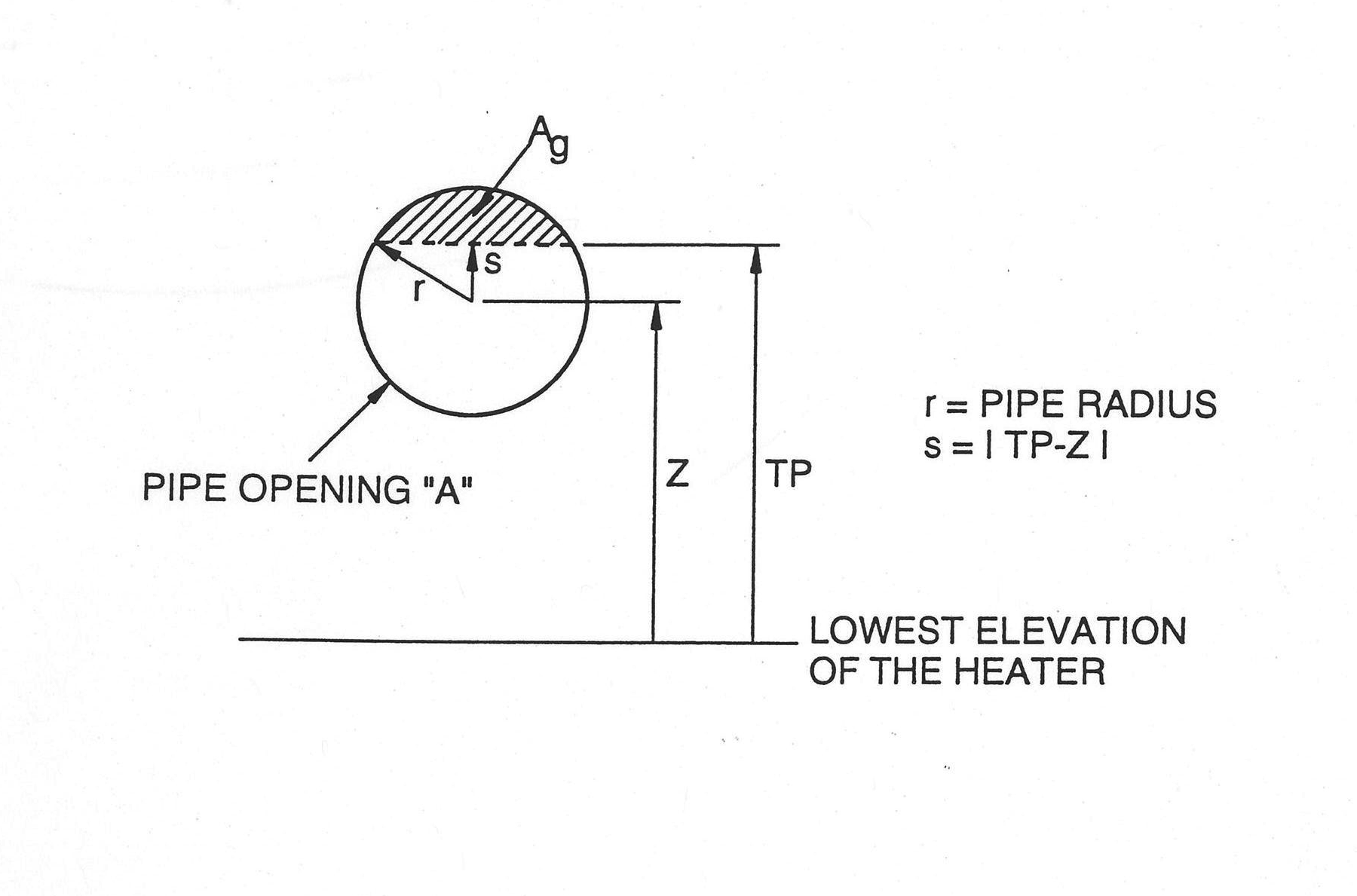
Figure 7.4.2 Area-Weighted Two-Phase Outflow Quality
Since β is defined as
the quality can be expressed in terms of density and void fraction by rearranging Eq. (7.4-1) and using the fact that α=β,
where
if the two-phase interface is higher than the center of the pipe but lower than the top of the opening, or
if the two‑phase interface is lower than the center of the pipe but higher than the bottom of the opening. The above area‑weighted quality evaluation method also applies to all of the other heaters for treating two‑phase outlet flow.
The two‑phase interface of the heater has to be known before deciding the need to evaluate the area‑weighted outlet flow quality. To determine the two-phase interface, the shell‑side quality, xs, of the heater has to be found first, which is calculated according to the enthalpy of the heater since the heater is at the saturation pressure, i.e., both the saturation enthalpies of the liquid and the vapor can be obtained from the known saturation pressure. Then, the two‑phase interface TP is simply
where M is the heater total mass, As is the heater cross section, ρs is the heater density, and Hs is the heater height.
The deaerator must cope with small imbalances between incoming and outgoing energies in the steady state. These imbalances are caused by minor inconsistencies between user‑specified thermodynamic conditions and the SASSYS-1 correlations for the thermodynamic properties. This problem is solved by the introduction of a pseudo‑heat conduction energy transfer term. The temperature gradient between the heater and the ambient conditions serves as the driving force, and the code computes a pseudo‑heat transfer coefficient which will give a steady‑state energy balance. The coefficient is positive if energy is accumulating and negative if energy is draining. This coefficient is then kept constant throughout the transient. In formula form, the pseudo-coefficient can be expressed as
where Ts is the saturation temperature of the heater and T∞ is the ambient temperature. The other heater models deal with the imbalances this same way.
The thermal‑hydraulic effects of noncondensible gas on the model are neglected and the heat conductor term is not applied.
7.4.2.2. Analytical Equations
The applicable mass and energy equations for the deaerator are the same as those used in Section 7.2, so they will not be reiterated here. However, it should be noted that, unlike the volumes described in Section 7.2, there is strict separation of liquid and vapor in the deaerator, and so outgoing flow enthalpies are affected by the elevation of the flow outlet. Calculations of outgoing flow enthalpies must take into account whether the outgoing flow is strictly liquid, strictly vapor, or a two‑phase mixture if the outlet intersects the two‑phase interface.
The separation of the phases affects the following equation, relating the change in compressible volume pressure to the changes in the flows in each of the segments attached to the volume, which is simply Eq. (7.2-47) in Section 7.2,
The superscript n which denotes the time step, will be omitted for simplicity in the following discussion. Previously, in a volume with perfectly mixed two‑phase fluid, the term hj, which is the enthalpy of segment j attached to volume l, has the same enthalpy as volume l if segment j leads flow out of volume l; hj is the enthalpy transported along segment j from the volume preceding segment j if fluid flows through segment j into volume l. Now, for the current heater volume, perfect mixing of two‑phase fluid no longer exists and immediate separation of liquid from vapor is assumed to take place, so the value of hj will be different from the mixture enthalpy of volume l due to the existence of the two‑phase interface. That is, depending on the relative positions of segment j (pipe) and the two-phase interface, segment j may contain pure vapor, pure liquid, or two‑phase fluid with an area‑weighted quality determined by the scheme described in Section 7.4.2.1. Therefore, if segment j is an outlet segment, hj can be hl,g, the vapor enthalpy of volume l when the opening of segment j is higher than the two-phase interface; or hl,f, the liquid enthalpy of volume l when the opening of segment j is lower than the two‑phase interface; or else hl,f+x(hl,g−hl,f), where x is the area-weighted quality when the two‑phase interface lies within the segment opening. On the other hand, if segment j is an inlet segment, hj will have to be determined according to which of the three possible situations exists in the volume at the inlet to segment j rather than in volume l. It is also possible that hj may just be the transported enthalpy of the preceding volume if the preceding volume is not a heated volume but a volume with fluid of perfect mixing.
For two‑phase flow in the pipe, the momentum equation is again basically the same as for single‑phase flow except that a two‑phase multiplier, which is a function of both quality and pressure, has to be included wherever a two-phase flow is present in the segment (e.g., pipe) to adjust the friction factor for modeling pressure drop. See Section 7.2 for the discussion of this empirically‑determined multiplier. One more thing to mention regarding the energy equation is that the source term Ql in Eq. (7.4-7) is computed explicitly as (Ts − T∞)Upseu, where Upseu is determined in the steady state by Eq. (7.4-6). Ts is the saturation temperature of the heater in the previous time step and T∞ is the constant ambient temperature specified by the user in the steady state.
7.4.3. Steam Drum
A steam drum is mainly used to separate two‑phase fluid from the recirculation loop and then provide saturated steam to the superheater. Like the deaerator, a steam drum is categorized as an open heater.
7.4.3.1. Model Description
The physical configuration of a steam drum is similar to that of a deaerator except that it is a cylinder now lying on the side, as depicted in Figure 7.4.3. The call for an appropriate response when the two‑phase interface falls within the pipe opening as well as the need for coping with small imbalances between incoming and outgoing energies are handled the same way as previously described in the deaerator model.
Predicting the level of the two‑phase interface in transients is a difficult problem in a heater of this configuration because the cross‑sectional area parallel to the cylinder axis varies in the vertical direction (remember, the cylinder is lying on the side), and so the two‑phase interface must be found from a transcendental equation. Since the steam drum is a right circular cylinder, it is obvious from the end view in Figure 7.4.3 that the ratio of Ag to Ag plus Af is the void fraction αs, i.e.,
where Ag is the projected area occupied by the vapor and Af is the area by liquid. By taking a similar approach to that carried out in Section 7.4.2.1 and bearing in mind that the cross‑sectional area of the entire cylinder is now under consideration, rather than just the opening of a pipe which is attached to the heater as depicted in Figure 7.4.2, equations of the same form as Eq. (7.4-3) and Eq. (7.4-4) are obtained,
and
where L=|TP−CV|.
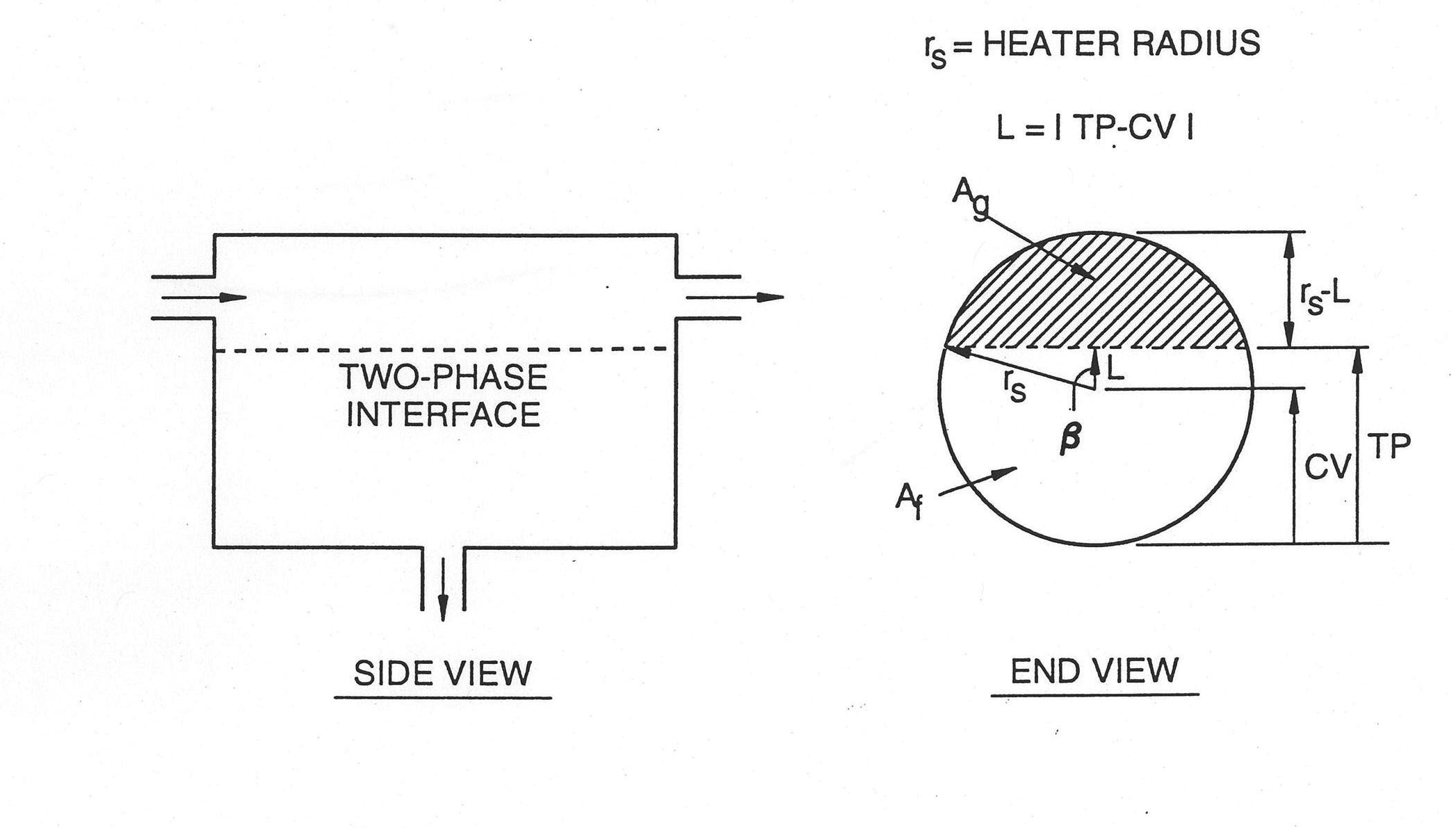
Figure 7.4.3 Steam Drum
The difference between Eq. (7.4-3) and Eq. (7.4-8) (or Eq. (7.4-4) and Eq. (7.4-9)) is that s on the right-hand side of Eq. (7.4-4) is a known quantity and α is to be found, which in turn yields the pseudo-quality x for the outgoing flow, whereas in the current situation, L in Eq. (7.4-8) is an unknown and αs is already known from the corresponding quality xs by the relation αs=xsvg/v. The quality xs is simply calculated from the updated heater pressure and enthalpy. Thus, Eq. (7.4-8) or Eq. (7.4-9) becomes a transcendental equation to be solved for the two‑phase interface, TP.
A noniterative scheme has been developed to solve this equation. See Section 7.7.3 for a description of this scheme.
7.4.3.2. Analytical Equations
As is obvious from the similarity in the configurations of the deaerator and the steam drum, what is described in Section 7.4.2.2 about the analytical equations for the deaerator is also applicable to the steam drum model.
7.4.4. Condenser
Beginning with this section, a total of six closed heaters including condenser, reheater, flashed heater, drain cooler, desuperheating heater, and desuperheater/drain cooler will be described. The term “closed heater” indicates that hot and cold fluids are separated between a shell side and a tube side. Heat transfer occurs across the tube without contact between hot and cold fluids. Closed heaters consist of a closed volume, or shell side, and a tube bundle, or tube side. Flow is carried into and out of the tube bundle by pipes which lie outside the heater boundary. The condenser is the simplest one among these closed heaters, and it is used to convert steam from the turbine to liquid.
7.4.4.1. Model Description
As diagramed in Figure 7.4.4, a condenser is a box with a tube bundle passing horizontally through it; this is essentially a deaerator with a tube bundle running through the vapor region. The tube bundle may have bends in it. The fluid on the tube side is assumed to be single phase. The tube bundle is assumed to be contained entirely in the vapor region, so a condensation heat transfer coefficient is used on the shell side under the normal conditions when the temperature on the tube side, in which river water or cooling fluid flows, is lower than the shell‑side vapor temperature. The model also includes the contingency to use a shell‑side heat transfer coefficient computed from the Dittus‑Boelter equation (Ref. 7-4),
in case the tube‑side temperature is higher than that on the shell side, as in an accident or any unfavorable transients. In either case, the heat transfer coefficient must be adjusted in the steady state so that the tube‑side temperature distribution is consistent with the temperatures in the remainder of the plant, i.e., the temperatures at the tube inlet and outlet coincide with the user‑specified temperatures.
The heat transfer coefficient on the tube side is calculated using the Dittus‑Boelter equation. Heat transfer between the tube side and the shell side is assumed to take place through the mechanism of radial conduction only; axial conduction is neglected. This radial conduction assumption for the tube bundle is made for all of the closed heater models.
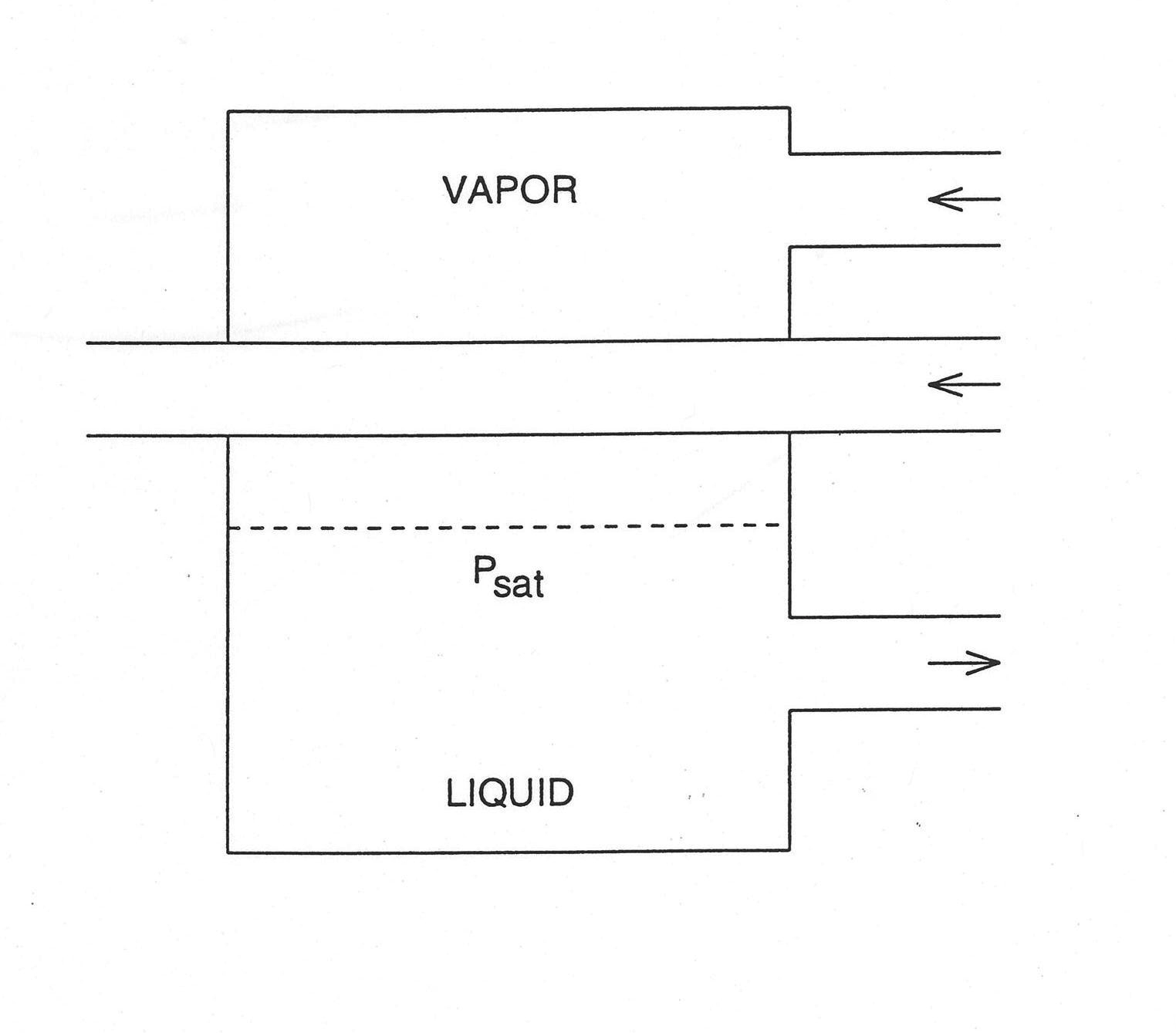
Figure 7.4.4 Condenser
7.4.4.2. Analytical Equations
The mass and energy equations for the shell side of the condenser are the same as those used in the open heaters, and these equations are also valid for the shell side in all the closed heaters. Also, the same momentum equation used in Section 7.2 is again applicable to the tube side (the heated section of the flow segment) of the condenser and other closed heaters. Naturally, the two-phase friction multipliers should be included whenever an inlet or outlet pipe contains other than single‑phase fluid. In addition, a simplified energy equation based on the first law of thermodynamics is needed for the heated tube element, i.e., the tube side fluid and the metal tube itself.
For the tube side fluid, the energy equation can be expressed as
if the kinetic energy and potential energy are negligible.
For the metal tube, the energy balance has the form,
7.4.4.3. Discretized Equations
The tube side is discretized as shown in Figure 7.4.5, and the temperature distribution on the tube side is determined using the differenced form of the first law of thermodynamics,
where
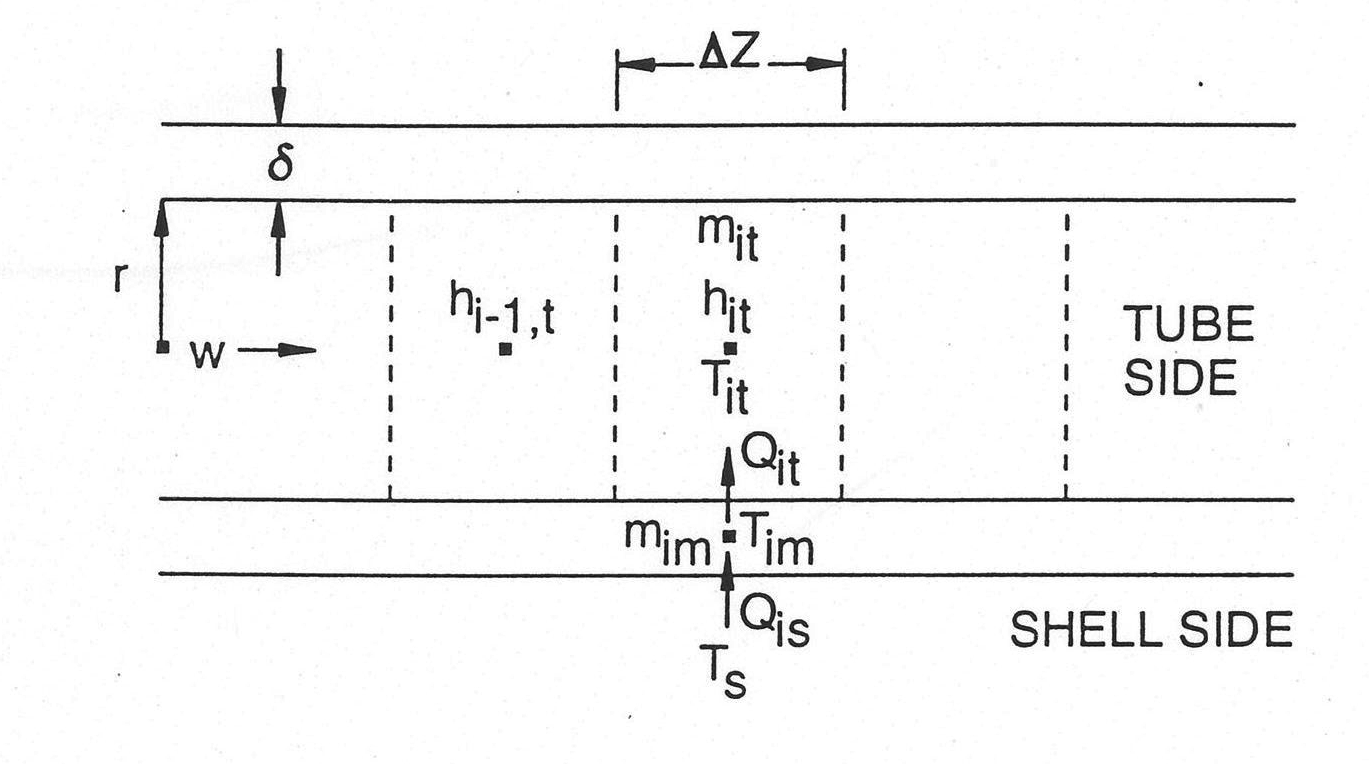
Figure 7.4.5 Tube-side Nodalization
The metal tube temperatures Tim are computed from a similar set of equations,
and
Note that Ts, the shell-side temperature, is considered to be uniform throughout the entire heater volume, whether in the steam region or in the liquid region, and that the specific heat and the thermal conductivity of the metal tube are assumed to be constant within the temperature range under consideration. The thermal resistance on the tube side, Rt, is the same at each node along the tube side but on the shell side, Ris, may vary node to node along the shell side if the tube is partially submerged in the liquid region. When the shell side is hotter than the tube side, it is assumed that no local boiling occurs on the tube side and that the condensate does not form a wetted perimeter along the tube outer periphery.
The updated fluid enthalpy at each node is calculated explicitly using quantities at the previous time step, so from Eq. (7.4-13) it can be expressed
where
Similarly, Eq. (7.4-15) can be rewritten in explicit form for updating the metal tube temperatures at each node,
where
The superscript n in Rnt denotes that the tube side heat transfer coefficient ht is a function of time, i.e., hnt, whereas the metal thermal conductivity km is assumed to be constant throughout the transient. This is also true for his and km in Ris.
The tube‑side fluid temperature Tnit in Eq. (7.4-18) is readily computed according to the equation of state from the fluid enthalpy and pressure at each node, and Tns is just the saturation temperature of the shell side fluid in the heater.
All of the terms on the right‑hand side of Eq. (7.4-17) are known from the previous time step, so hn+1it can be updated, which will then yield Tn+1it for use in Eq. (7.4-18) in the next time step. Tn+1im on the other hand is determined independently from Eq. (7.4-19), with Qnis and Qnit given respectively by Eq. (7.4-18) and Eq. (7.4-20). The link between the condenser model and the rest of the balance‑of‑plant models is made through the heat source terms, i.e., Qnl in Eq. (7.4-7) and Qnl in Eq. (7.4-20). The summation of Qnis at each node along the shell side is in fact the negative of the heat source term Qnl for the heater in Eq. (7.4-7). The sign change reflects the fact that Qis should be a heat sink term for the heater when the shell side temperature is higher than the tube side temperature.
7.4.5. Reheater
A reheater is used to improve turbine performance by reheating the moist steam to the superheated phase as it passes between stages of the turbine.
7.4.5.1. Model Description
The basic features of a reheater are depicted in Figure 7.4.6, for illustrative purposes it is a right circular cylinder standing on end. The shell side is assumed to be at a lower temperature than the tube side. In this type of heater, the shell side is all vapor, and the reheater appears to be little more than the vapor section of a condenser with a vertically bent tube bundle. However, there is one important difference: the fluid on the tube side changes phase from steam to two‑phase as it passes through the reheater. Modeling this phase transition requires use of the energy equation; however, the energy equation in the balance‑of‑plant formulation is solved at flow junctions (such as the shell side of a heater), not along flow paths (such as the tube side). Therefore, the reheater is modeled in the configuration shown in Figure 7.4.7. The shell side of Figure 7.4.6 becomes the tube side in Figure 7.4.7, with steam which is being heated flowing within the tube, and the tube side of Figure 7.4.6 becomes the shell side in Figure 7.4.7. The shell side of Figure 7.4.7 then easily models the phase transition which occurs in the tube side of the reheater.
The reconfiguration of the reheater to Figure 7.4.7 is done so as to conserve volume on both sides of the heater. The height, H, of the cylinder in Figure 7.4.7 is now taken as the difference between the elevations of the highest tube and the lowest tube in the tube bundle of the original configuration in Figure 7.4.6. Therefore the cross sectional area As on the shell side in Figure 7.4.7 is determined as
where Vt is the internal volume of all tubes in the tube bundle in Figure 7.4.6. Furthermore, the mass of the metal tube, mim, in each node in Figure 7.4.7 is obtained by dividing the total metal mass of all original tubes, Mm, by H and then multiplying by the node length Δz,
Similarly, the internal tube surface area in each node is computed based on the total internal heat transfer surface of all tubes, At, in Figure 7.4.6 to be (At/H)Δz. Both the inside radius and the outside radius of the tube in Figure 7.4.7 are also needed for use in equations like Eq. (7.4-14) and Eq. (7.4-16) in order to compute heat transfer across the tube boundaries. The inside radius is readily calculated using the internal tube surface area in each node just described above. From the relationship, 2πrΔz=(At/H)Δz, the inside radius ri is computed as
and the outside radius can then be deduced by making use of Eq. (7.4-21) to be
where ρ is the metal density which is assumed to remain the same throughout the reconfiguration.
The model of Figure 7.4.7 is very similar to a condenser except that the tube side is vertical instead of horizontal. This means that the tube passes through both liquid and vapor. Since the tube side vapor is heated by the shell side fluid, the heat transfer coefficient on the shell side his is computed from the Dittus‑Boelter correlation in the liquid region and a condensation coefficient in the vapor region. Usually, the two‑phase interface will fall within one of the nodes which discretizes the tube side; in this case, the heat transfer coefficient within the node is an area‑weighted combination of the condensation coefficient and the Dittus‑Boelter coefficient.
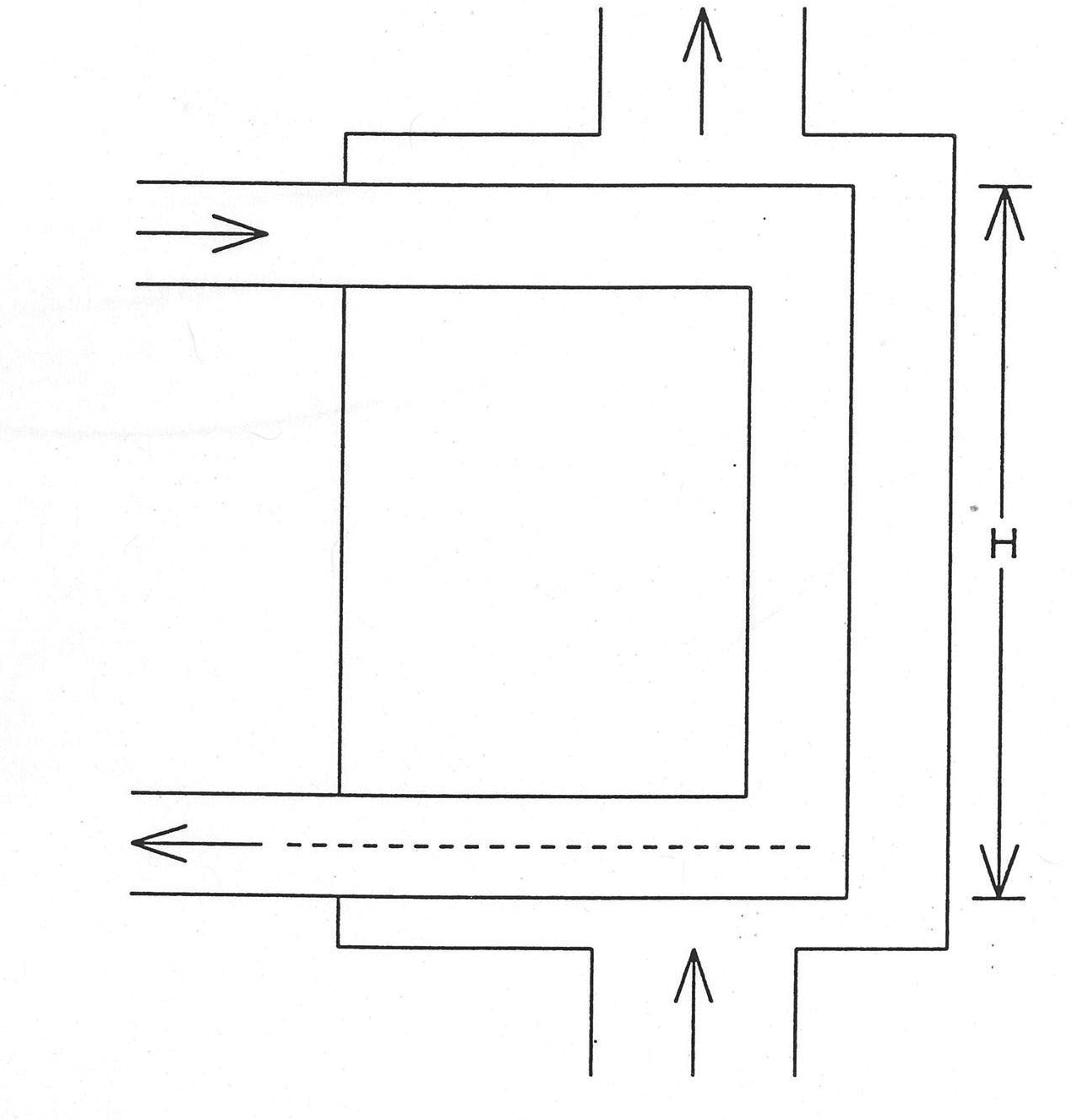
Figure 7.4.6 Reheater
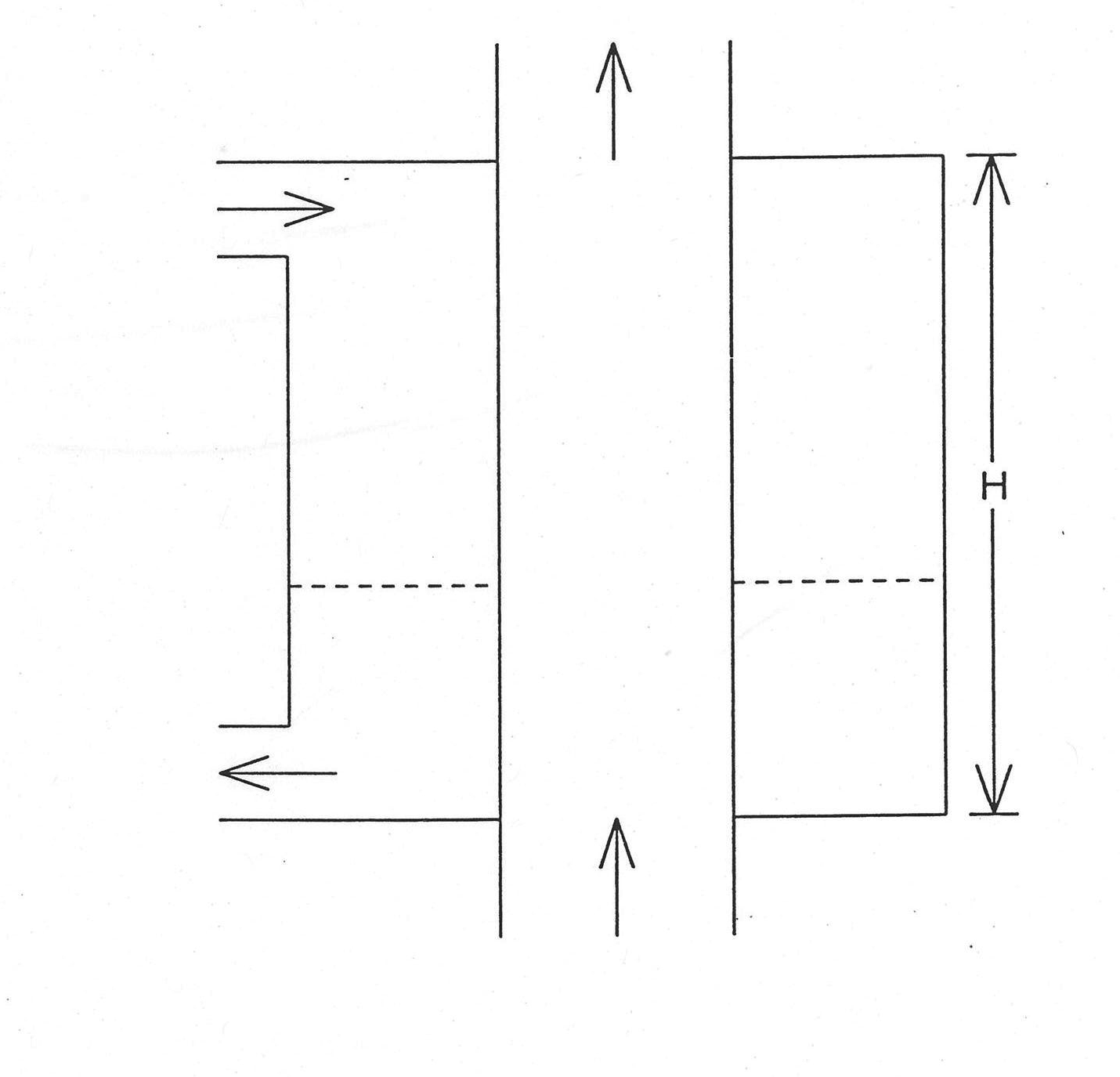
Figure 7.4.7 Reconfiguration of the Reheater
7.4.5.2. Analytical Equations and Discretized Equations
The equations discussed in Section 7.4.4.2 and Section 7.4.4.3 for the condenser model also apply to the reheater model and to the remaining closed heater models. The only difference between the energy equations for the condenser and reheater models is in the calculation of the shell‑side heat transfer coefficient, as described in Section 7.4.5.1.
7.4.6. Flashed Heater
A flashed heater is needed when liquid upstream of the heater shell side is above the shell side saturation point. The flashed heater allows the liquid to flash safely upon entering the heater.
7.4.6.1. Model Description
The geometry of the flashed heater is given in Figure 7.4.8. This is a right circular cylinder lying on the side, with a U‑shaped tube bundle that is partially submerged in liquid and partially surrounded by vapor. The bundle enters and leaves the shell side through one end of the cylinder, with the entrance and exit at two different elevations. The tube‑side fluid is assumed single phase, and fluid can enter at either the lower or the upper elevation. These assumptions are also made in the drain cooler, desuperheating heater, and desuperheater/drain cooler models to be described in subsequent sections. Therefore, there are two bends in the tube, and the tube is considered to consist of three sections: two horizontal ones of equal length and a vertical one of length equal to the distance between the elevations of the tube entrance and exit.
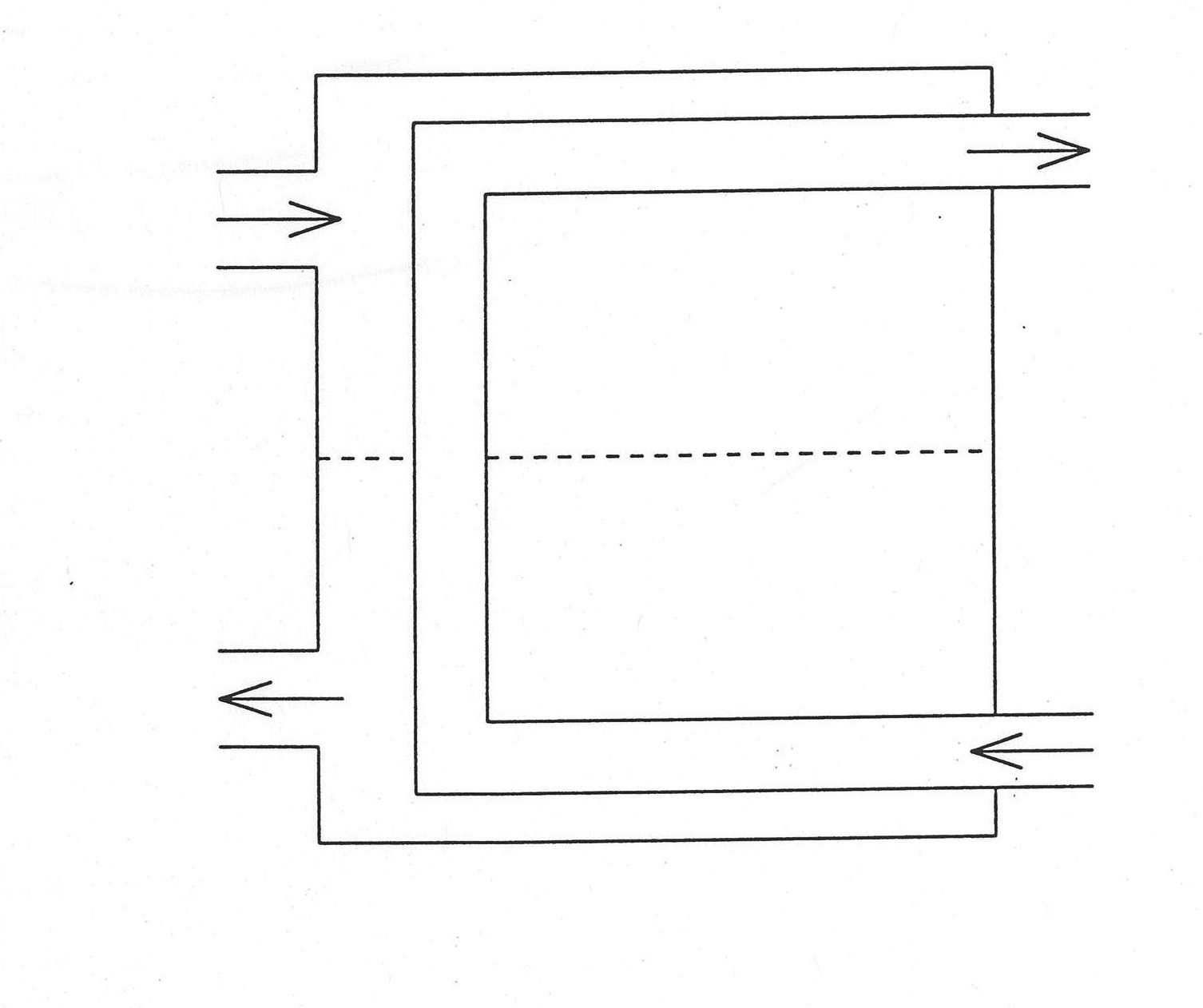
Figure 7.4.8 Flashed Heater
7.4.6.2. Analytical Equations and Discretized Equations
As discussed in Section 7.4.5.2 for the reheater model, the equations of Section 7.4.4.2 and Section 7.4.4.3 also apply to the flashed heater model. However, some details specific to the flashed heater need further explanation. The determination of the heat transfer coefficient on the shell side becomes more complicated due to the bending of the tube. The two‑phase interface will not only fall within one of the nodes as before in the reheater, but also might fall within many of the nodes when it reaches either of the two horizontal sections of the tube.
In the latter situation, the scheme of area‑weighted heat transfer coefficients is again used. In either of the situations, provision is made to handle the case when the tube side temperature is higher than the shell side temperature, an additional possibility likely to occur during transients. If the tube side is cooler than the shell side, the heat transfer coefficients along the tube surface are computed as for the reheater. If the tube side is hotter than the shell side, the coefficient within the vapor region is calculated from the Dittus‑Boelter correlation, and in the liquid region, a boiling heat transfer coefficient from the nucleate boiling regimes (Ref. 7-9)
is used. The tube side heat transfer coefficient is always calculated from the Dittus‑Boelter correlation no matter if the tube side is cooler or hotter than the shell side, i.e., assuming no phase change on the tube side in any case.
Predicting the level of the two‑phase interface is a complicated problem in a heater of this configuration for two reasons. First, as in the steam drum, the cross‑sectional area parallel to the cylinder axis varies in the vertical direction, and so the two‑phase interface must be found from a transcendental equation. See Section 7.7.3 for the noniterative scheme to solve this equation. Second, the volume taken up by the tube bundle must be considered when determining the two‑phase interface. In order to simplify the calculations, the void fraction is taken to be the ratio of the vapor volume divided by the vapor volume plus the liquid volume (rather than dividing by the total volume, which is the sum of the volumes of vapor, liquid, and tube bundle) when the interface falls between the bundle inlet and outlet, i.e.,
where x is known once the new volume pressure and enthalpy are updated. Eq. (7.4-8) (or Eq. (7.4-9)) can then be combined with Eq. (7.4-23) to solve for the two-phase interface.
7.4.7. Drain Cooler
When the shell side outlet liquid from a heater must be sufficiently subcooled so as to remain liquid at the lower pressure of a downstream component, a drain cooler is needed.
7.4.7.1. Model Description
As shown in Figure 7.4.9, the drain cooler configuration is identical to that of the flashed heater with the addition of a drain built into a lower corner of the cylinder. The top of the drain extends horizontally across the cylinder perpendicular to the cylinder axis (see end view in the same figure). The drain is separated from the remainder of the shell side except for a flow inlet which brings saturated liquid from the heater into the drain. This flow inlet is assumed to be always submerged in the saturated liquid, and calculation will be stopped whenever the two‑phase interface drops below the inlet and uncovers it, since this might cause the subcooled fluid to flow out of the drain and into the shell side of the heater. There is also a flow outlet which carries liquid out of the drain and away from the heater. Liquid within the drain is always assumed to be subcooled at the saturation pressure of the shell side of the heater. Inlet and outlet flows are assumed to be nearly equal during a transient, for no phase‑change is allowed in the drain and thus flow may be assumed incompressible. One end of the tube bundle passes through the drain, as seen in Figure 7.4.9. The tube‑side fluid can enter at either the lower or the upper elevation.
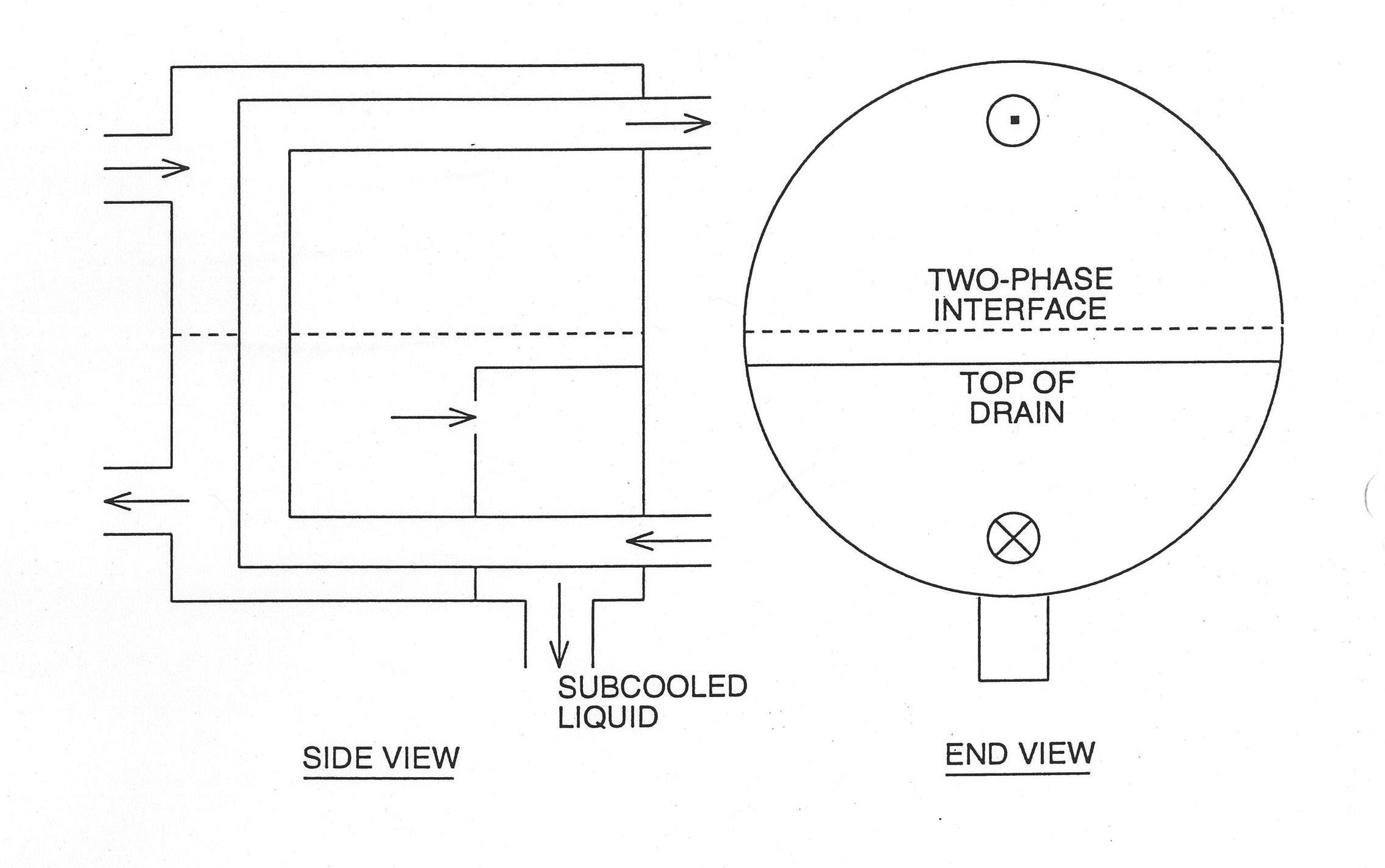
Figure 7.4.9 Drain Cooler
7.4.7.2. Analytical Equations and Discretized Equations
For the part of the drain cooler outside the drain, the discussion in Section 7.4.6.2 about the flashed heater is applicable to the drain cooler model. Nevertheless, there are two further points to be noted. First, although the fluid flowing out of the drain through the pipe which is attached to the drain has the same enthalpy as that of the subcooled liquid in the drain, the energy being lost from the shell side of the heater is actually the saturation enthalpy of the shell side liquid. Therefore, the term hnj in Eq. (7.4-7) has to be equal to the saturated liquid enthalpy. When j corresponds to the outlet flow segment from the drain in order for this equation to compute the shell‑side pressure change correctly. On the other hand, the fluid enthalpy being transported from the drain to the next component must be set to the subcooled liquid enthalpy of the drain. Second, the heat source term Ql in Eq. (7.4-7) will now have contributions only from the heat transfer through the boundaries of the tube bundle outside the drain. The energy heat transfer occurring across the tube boundaries within the drain will be considered as QD of the drain to be used in Eq. (7.4-24) below.
A one‑node energy equation,
is currently used on the shell side along the tube within the drain. Plans are to add a multi‑node energy equation on the shell side to improve the treatment of the energy balance within the drain, which is especially important in the counterflow situation. On the tube side, the multi‑node treatment is retained.
In discretized form, Eq. (7.4-24) is rewritten as,
where hnin is the saturated liquid enthalpy and hnout in the current one‑node treatment, is actually hnD. QnD is the summation of the contributions from all the nodes within the drain, i.e.,
with
where
Note that RniD is simply RnD and TniD merely TnD in the current one‑node treatment on the shell side within the drain, which means hniD is equal to hnD. QnD is calculated explicitly.
For the tube side within the drain, Eq. (7.3-17) and Eq. (7.4-18) are used, and Eq. (7.4-19) is applied to the metal tube within the drain, with Qnis in Eq. (7.4-15) replaced by QniD from Eq. (7.4-27).
Within the drain, a heat transfer coefficient hnD is computed from the Dittus‑Boelter equation on the shell side of the tube surface, regardless of whether the tube side is hotter or colder than the shell side.
Adjustments are made separately to the drain and to the remainder of the shell side in order to achieve a steady-state energy balance which is consistent with conditions in the remainder of the plant. First, the code computes a calibration factor to adjust the tube surface heat transfer area within the drain. Then, energy is balanced in the remainder of the heater by computing a separate factor plus a pseudo‑heat transfer coefficient as described previously.
7.4.8. Desuperheating Heater
A desuperheating heater is needed when the steam entering the heater shell side is highly superheated. The entering steam is initially contained in a desuperheating region, where it transfers heat to the tube side fluid rather than dissipating heat to the shell side saturated steam. Steam moving from the desuperheating region to the main section of the shell side is near saturation. The desuperheating region also protects the remainder of the heater from being damaged by highly superheated steam.
7.4.8.1. Model Description
The desuperheating heater is diagrammed in Figure 7.4.10; it can be summed up as a drain cooler turned upside down. Instead of a drain at the bottom, it has a desuperheating region built into an upper corner. The desuperheating region is filled with superheated vapor at the saturation pressure of the heater two‑phase interface. Normally, the tube side is filled with a single-phase fluid which is cooler than the vapor in the desuperheating region; the model also allows the tube side temperature to be higher than the shell side temperature, within or outside the desuperheating region. The desuperheating heater model does not handle the situation when the two‑phase interface reaches the outlet of the desuperheating region, which might cause the desuperheating region to be partially filled with liquid. If the two‑phase interface reaches this point, the calculation is stopped. All other aspects of the drain cooler model, such as inlet and outlet flows of the drain are nearly equal and the tube‑side fluid can enter at either of the tube ends, apply to the desuperheating heater.
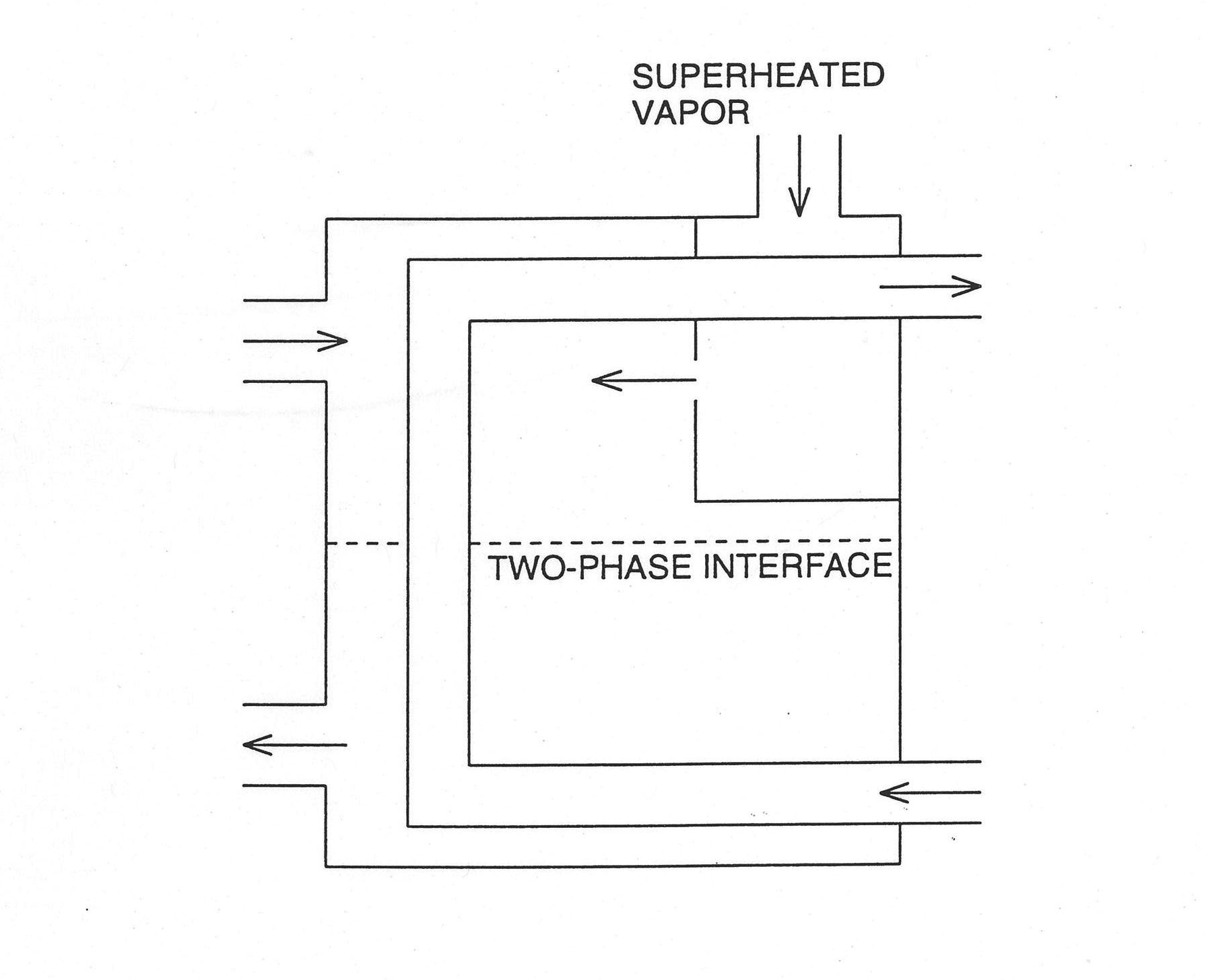
Figure 7.4.10 Desuperheating Heater
7.4.8.2. Analytical Equations and Discretized Equations
All the aspects described in Section 7.4.7 for the drain cooler model are applicable to the desuperheating heater and, wherever necessary, the subscript D for the drain should be replaced by DS for the desuperheating region, such as in Eq. (7.4-24) to Eq. (7.4-28). However, it should be noted that the term hnj in Eq. (7.4-7) now is the superheated steam enthalpy of the desuperheating region when j corresponds to the inlet flow segment into the desuperheating region.
7.4.9. Desuperheater/Drain Cooler
7.4.9.1. Model Description
This heater is pictured in Figure 7.4.11 and is a combination of the drain cooler and the desuperheating heater. All details discussed in Section 7.4.7.1 and Section 7.4.8.1 for these two models apply also to the desuperheater/drain cooler.
7.4.9.2. Analytical Equations and Discretized Equations
All aspects described in Section 7.4.7.2 and Section 7.4.8.2 for the drain cooler and the desuperheating heater are applicable to the desuperheater/drain cooler. Three additional points to note are that 1) the mass flow rate entering the desuperheating region can differ from that entering the drain, 2) separate calibration factors are used in the desuperheating section and in the drain for adjusting the tube surface heat transfer area to conserve energy, and 3) the heat source term Ql in Eq. (7.4-7) will now have contributions only from the energy transferred across the boundaries of the tube bundle outside the desuperheating region and the drain.
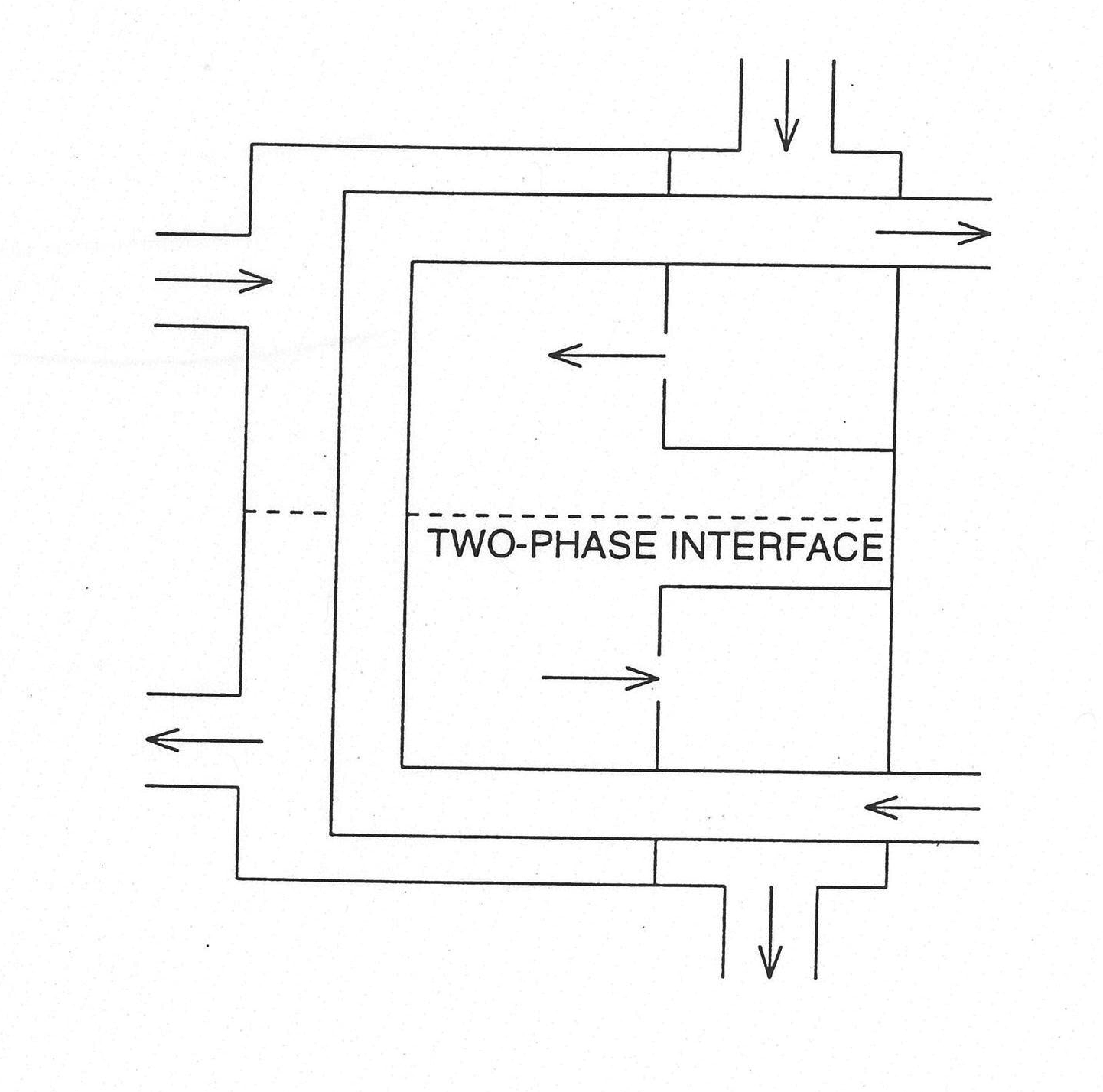
Figure 7.4.11 Desuperheating/Drain Cooler
7.4.10. Turbine
A turbine is a device in which energy is removed from the fluid as a result of work performed by the flow; it actually is composed of many stages driving one rotor which extracts work from the flow. The stages are connected by nozzles which permit both non-choked and choked flow. Compressible flow is now very important in describing the flow behavior in the nozzles.
7.4.10.1. Model Description
The basic features of a turbine are depicted in Figure 7.4.12. This schematic shows two of the stages connected by nozzles driving one common rotor which in turn drives a generator. Also shown in the figure are the extraction steam ports, in which the steam is treated as incompressible flow. A series of volumes is used to model the various stages in the turbine, and each individual stage is represented by a compressible volume. There is no limit on the number of turbine stages so long as it does not exceed the maximum number of compressible volumes allowed in the code. Nozzles are modeled by special segments using a different form of the momentum equation from that discussed in Section 7.2 in order to account for the characteristics of the compressible flow. Separate expressions based on thermodynamic conditions at the inlet alone, when the flow is choked, or at the outlet as well, when the flow is nonchoked, are used to compute the nozzle flow. These correlations will be discussed in detail in Section 7.4.10.2.
Turbine efficiency is based on losses to isentropic expansion, and shaft work is then calculated using quasi‑empirical correlations for stage efficiency. Stage efficiency is affected by many loss factors, such as rotation loss, moisture loss, nozzle‑end loss, etc., but only rotation loss and moisture loss are included in the current model because they are significant losses and their functional formulations are known. More loss factors will be included in future model improvements.
7.4.10.2. Analytical Equations
The assumption that the liquid and vapor are strictly separated in the heater models reported above does not apply to the turbine model. Instead, perfect mixing within the compressible volumes which model the turbine stages is now adopted due to the movement of the rotating blades; this is the same assumption made for the energy equation governing the compressible volumes discussed in Section 7.2. Both the mass and the energy equations used in the turbine model are the same as those used in the heater models and in Section 7.2 except that the energy equation used in the turbine model has an additional term included accounting for the energy loss through the work done by the turbine.
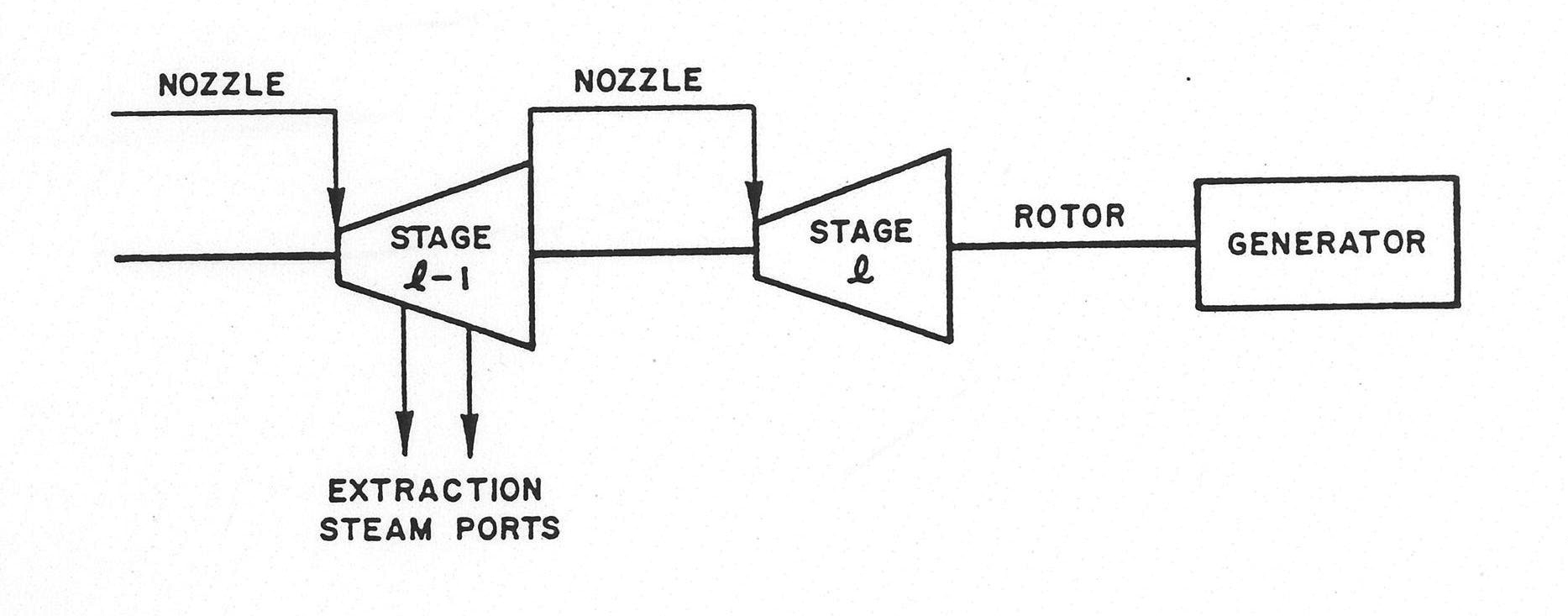
Figure 7.4.12 Turbine
For simplicity, look first at the energy equation used in the heater models,
which is simply the same equation as Eq. (7.2-6). Then by integrating this equation over the entire volume Vl for each volume l and writing a separate energy equation for each volume with the work term added, Eq. (7.4-29) becomes
when the work term Hl is in terms of turbine efficiency based on losses to isentropic expansion and is expressed as
where ηl is the stage efficiency, win is the flow rate at the inlet nozzle, and Δ¯hlis the loss due to isentropic expansion, defined as
Note that ¯hl is evaluated at P=Pl and s=sl−1, which is the entropy at the previous stage l−1.
Fundamentals of the turbine thermodynamics are given in many standard books and Salisbury (Ref. 7-10) discusses the subject comprehensively.
The stage efficiency ηl is just the blade efficiency ηl,B minus loss factors from rotation (Rl,R) and moisture (Rl,m),
where R_{misc} represents all other minor losses currently not considered. In addition, an exhaust loss term has to be included in the right‑hand side of Eq. (7.4-33) if the turbine stage is the last stage of the turbine. The exhaust loss is expressed as
where V_{exit} is the velocity leaving the last stage and K_{E} is the exhaust loss constant.
The blade efficiency is defined as the ratio of the energy transfer to the blades to the theoretically available energy at the nozzle. From the velocity vector diagram shown in Figure 7.4.13 (the variables in the figure are explained in the context), the rate of energy transfer from the steam to the blades is obtained as the product of the blade velocity V_{B} and the force F exerted by the steam on the blades. The available energy (rate) at the nozzle is simply the kinetic energy in the isentropic expansion of the steam. Therefore,
where win is the same as in Eq. (7.4-31) and V_{o} is the theoretical nozzle (steam) velocity in the isentropic expansion. By the principle of impulse and momentum, the force on the blades is equal to the steam flow rate w_{in} multiplied by the total change in steam velocity, relative to the blades, i.e.,
where V_{a} and V_{b} are the steam velocity relative to the blade and parallel to the motion of the blade at the blade entrance and exit, respectively, as indicated in Figure 7.4.13. The plus sign in Eq. (7.4-35) indicates, as a result of the vector operation, that V_{a} and V_{b} are in opposite directions. Substituting Eq. (7.4-35) into Eq. (7.4-34) thus gives the blade efficiency as
The actual velocity V_{1} of steam leaving the nozzle is slightly less than V_{o} and becomes even smaller when the effect of reaction, i.e., energy released in the bucket (Ref. 7-10), is considered. Thus,
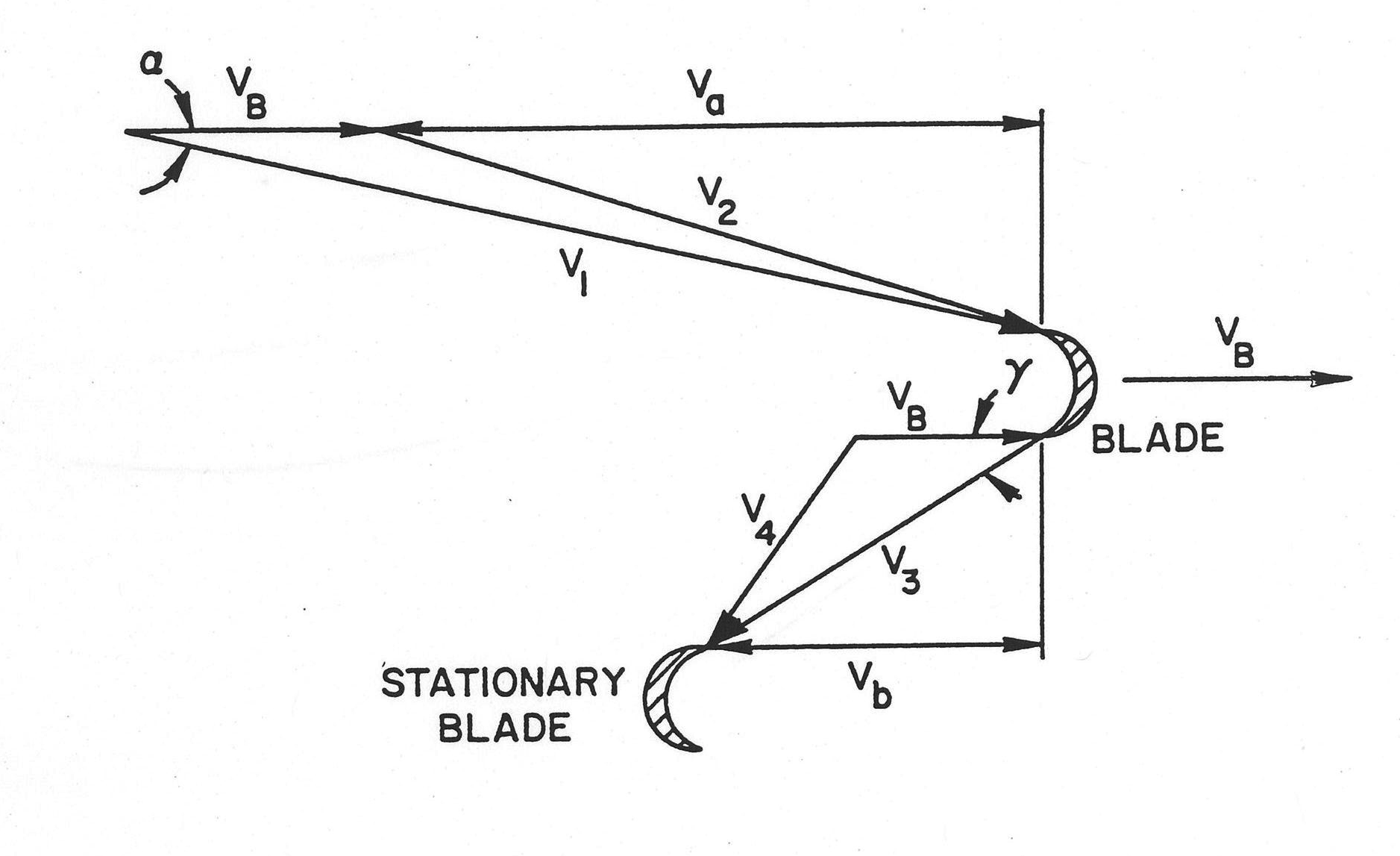
Figure 7.4.13 Velocity Vector Diagram for Single Row of Moving Blades
with a\ \equiv \ \left( 1 - x \right)^{1/2}\ , C_{n} the nozzle velocity coefficient, and x the fraction of stage energy released in the bucket system.
In an actual turbine system, it is impossible for the entrance angle of the steam to the blades system to be horizontal or in the plane of the wheel; otherwise, there would be mechanical interference between the rotating blades and the nozzle. Therefore, the steam has to leave the nozzle at a nozzle angle \alpha, as shown in Figure 7.4.13. Furthermore, it is impossible for the steam to exit the blades at an angle of zero with respect to the plane of rotation of the blades; otherwise, there would be no way for the flow of steam to progress axially through the turbine. Thus, the blade exit angle \gamma in Figure 7.4.13 provides an axial leaving velocity component perpendicular to the plane of rotation of the blades for the exit velocity V_{3}.
Two additional loss factors must also be considered in a real turbine system: the fraction of the kinetic energy entering the blades which is realized at the blade exit C_{b}^{2} and the fraction of the stage energy released in the blades which is finally realized at the bucket exit, C_{r}^{2}. The exit velocity can then be represented (Ref. 7-10) by
in a single row of moving blades. For simplicity, C_{b} will be called the bucket coefficient, C_{r} the reaction coefficient, and x the reaction fraction. V_{3} is in fact the steam velocity at the blade exit, relative to the blade, while V_{2} is the steam velocity at the blade entrance, relative to the blade, and, by the law of cosines, is written as,
The absolute steam velocity at the blade exit, V_{4}, is then
In summary, by using the fact that
and
the blade efficiency in Eq. (7.4-36) can be rewritten explicitly, along with Eq. (7.4-37) to Eq. (7.4-39), as
Salisbury recommends the following expressions for the rotation loss and moisture loss:
and
where K_{l, R} is the rotation loss constant, K_{l, M} is the moisture loss constant, A_{l, n} is the nozzle area, and x_{l - 1} is the fluid quality at the previous stage l - 1. All the quantities used in Eq. (7.4-41) are volume dependent.
Since the work of the turbine is done through the rotors, which are aligned along a shaft to drive the generator, a relation has to be established between the turbine work and the rotor angular velocity \omega. The turbine work is a summation of the work by individual turbine stages, and the turbine work is related to the rotor angular velocity as,
where \tau_{T} is the turbine torque. The rotor angular velocity is changing during a transient according to the relative magnitudes of the turbine torque and the generator torque as follows,
where I is the turbine/generator rotor moment of inertia and \tau_{G} is the generator torque.
As mentioned in Section 7.4.10.1, the momentum equation used in the nozzle model is completely different from the one used in the heater models and in Section 7.2 because of the compressible flow considered for the nozzle. For nonchoked flow, the nozzle velocity is based on thermodynamic conditions at the inlet and at the outlet and is calculated from
where C_{n} is just the nozzle coefficient and \Delta \overline{h}_{l} is defined in Eq. (7.4-32), and the mass flux G is given by
where \overline{\rho}_{l} is the density evaluated at P_{l} and \overline{h}_{l}, i.e., \overline{\rho}_{l} = \overline{\rho}_{l} \left( P_{l}, \overline{h}_{l} \right) For choked flow, the nozzle velocity is based on thermodynamic conditions at the inlet only and is determined (Refs. 7-11, 7-12) separately for steam flow and for two‑phase flow as:
for steam:
when the criterion 0.545 P_{l - 1} \geq P_{l} is satisfied,
for two‑phase flow:
where
and
when the criterion P^{*} \geq P_{l} is satisfied. For both steam flow and two‑phase flow, the mass flux G is calculated by
Where \rho_{l - 1} is the density at the previous stage.
In the steady state, each of the user‑specified nozzle flow rates is compared to the calculated nozzle flow rate, which is the nozzle velocity, computed (according to the steady‑state pressure conditions) from one of the equations in Eq. (7.4-44), Eq. (7.4-46), and Eq. (7.4-47), multiplied by the user-specified nozzle area. If the calculated nozzle flow rate differs from the user‑specified nozzle flow rate, the computed nozzle velocity together with the user‑specified nozzle flow rate is used to adjust the user‑specified nozzle area, so that the two nozzle flow rates (computed and user‑input) will then be consistent. The adjusted nozzle area in the steady state is used for calculations throughout the transient. This flow area calibration algorithm is also used in the relief valve model, discussed in Section 7.4.11, to modify the user‑input relief valve flow area based on the user‑input relief valve capacity.
7.4.10.3. Discretized Equations
The energy equation for the turbine stage, Eq. (7.4-30), contains only an additional term, -H_{l}, compared with the energy equations for the heater models or for non‑heater compressible volumes Eq. (7.2-26). The work term H_{l} is written separately to emphasize the energy loss of the steam during isentropic expansion while driving the blades in the turbine stages; alternatively, H_{l} can be absorbed into the heat source term Q_{l} in Eq. (7.4-30), since it is only an energy term to be subtracted from the energy equation. Eq. (7.4-30) can then be rewritten as,
where Q_{l} now includes implicitly an energy loss due to the stage work. Eq. (7.4-50) has the same form as Eq. (7.2-26), and so Eq. (7.4-50) can be discretized in exactly the same way as Eq. (7.2-26); see Section 7.2 for details of the discretization.
The discretization of the momentum equation for nozzles is a complicated process, since the momentum equation now is entirely different from the one used in the previous models. In the existing solution scheme of the balance-of‑plant coding, the momentum Eq. (7.2-5) is rewritten, after discretization, such that the change in mass flow rate in each segment is expressed in terms of the changes in volume pressures at the segment inlet and outlet as,
Then an L \times L matrix equation is created by combining Eq. (7.4-51) and the discretized energy equation to solve for all L volume pressure changes simultaneously. In order to integrate the momentum equations for nozzles into the established matrix equation solution scheme, Eq. (7.4-44) to Eq. (7.4-49) have to be discretized to a form, similar to Eq. (7.4-51), relating flow changes to pressure changes in the volumes at the segment ends.
The derivation will begin with the momentum equation for nonchoked flow and proceed to choked flow, for which two separate treatments are needed for single‑phase (steam) and two‑phase flow.
Consider the flow rate w_{in} at the inlet nozzle to stage l as shown in Figure 7.4.12. By definition, the flow rate for nonchoked flow is the mass flux (or mass velocity) G in Eq. (7.4-45) multiplied by the nozzle area A_{n}; for brevity, w_{in} will be designated as w, V_{nz} as V, and A_{n} as A in the derivation. Thus,
Eq. (7.4-52) can be written in a differential form as,
where dV can be obtained from Eq. (7.4-44),
and d \overline{\rho}_{l} can be expressed as
with 1 / \overline{\rho}_{l} = \overline{v}_{l} \left(P_{l}, \overline{h}_{l} \right) which follows the definition of \overline{\rho}_{l} in Eq. (7.4-45). Substituting Eq. (7.4-54) and Eq. (7.4-55) into Eq. (7.4-53) yields, after rearranging,
Both d \overline{h}_{l} and d \overline{v}_{l} in Eq. (7.4-56) are related to the pressure of stage l as, respectively,
(remember, \overline{h}_{l} \equiv \overline{h}_{l} \left(P_{l}, s_{l - 1} \right) as seen in Eq. (7.4-32), and
By combining Eq. (7.4-56), Eq. (7.4-57), and Eq. (7.4-58), the finite change in flow rate can be rewritten as
At this point, it is assumed that the change in enthalpy in the previous stage \Delta h_{l - 1} can be expressed explicitly as a function of the change in pressure in stage l - 1 and the current time flows in the attached segments, without introducing unacceptable errors; that is, Eq. (7.2-33) can be simplified for the turbine stages (compressible volumes) by neglecting \Delta w_{j}, giving
Treating the stage enthalpy implicitly would result in a discretization form which is tediously complicated and cumbersome; however, this might be included in future model improvements.
The final discretization form is arrived at by replacing the subscript l with l - 1 in Eq. (7.4-60) and then using Eq. (7.4-60) in Eq. (7.4-59) to give
The two discretized momentum equations, Eq. (7.4-51) and Eq. (7.4-61) have analogous forms, as can be seen by comparing terms; for instance, \Delta t\ /\ \left[a_{o} - a_{3} \right] in Eq. (7.4-51) corresponds to wv_{l - 1} / \left(2 \Delta \overline{h}_{l} \right) in Eq. (7.4-61), and so on. Thus, when considering the volume pressure change due to the contribution of a nozzle segment, Eq. (7.4-61) becomes the counterpart of Eq. (7.4-51). Eq. (7.4-61) can be combined with the discretized energy Eq. (7.2-47) to render Eq. (7.2-55), which is expressed entirely in terms of changes in compressible volume pressures and is used to form the L \times L matrix equation system.
Since a functional form expressing enthalpy as a function of pressure and entropy is not available, the known expression for entropy as a function of pressure and enthalpy is used to compute the derivative terms \left(\partial \overline{h}_{l} / \partial P \right) and \left(\partial \overline{h}_{l} / \partial s \right) in Eq. (7.4-61). In the case of \left(\partial \overline{h}_{l} / \partial P \right) at s = s_{l - 1}, the derivative is calculated by using the known values of \overline{h}_{l} and P_{l} as the starting points and then iteratively searching for the other enthalpy value at pressure P_{l} plus a small increment and at entropy s_{l - 1}. The derivative \left(\partial \overline{h}_{l} / \partial s \right)_{P_{l}} is easier to obtain from
since entropy is a known function of pressure and enthalpy. In addition, the change in the entropy \Delta s_{l - 1} is also computed explicitly.
An alternative to calculating \Delta h_{l - 1} in Eq. (7.4-59) is to express \Delta h_{l - 1} in terms of the pressure and the entropy, i.e.,
Since h_{l - 1} = h_{l - 1} \left(P_{l - 1}, s_{l - 1} \right). Then, the discretization of the momentum equation becomes
The calculation of \left( \partial h_{l - 1} / \partial s \right) at P = P_{l - 1} (using an expression of the same form as Eq. (7.4-62)) in Eq. (7.4-64) and the calculation of the term \left\{l - 1, j \right\} in Eq. (7.4-61) probably take about the same amount of time. However, Eq. (7.4-64) is more time‑consuming to solve than Eq. (7.4-61) because of the need, to use the equation of entropy as a function of pressure and enthalpy, to evaluate \left( \partial h_{l - 1} / \partial P \right) at s = s_{l - 1} by iteration. In addition, Eq. (7.4-61) can be improved by expressing \left\{l - 1, j \right\} in an implicit form, whereas the additional \Delta s_{l - 1} term makes Eq. (7.4-64) more explicit (note the difference in the \Delta s_{l - 1} terms between the two equations). Currently, Eq. (7.4-61) is used in the turbine model.
For choked flow of steam, the flow rate at the inlet nozzle to stage l is obtained by multiplying Eq. (7.4-49) by the nozzle area,
where the nozzle velocity V is given in Eq. (7.4-46). In the following derivations for choked flow of steam, the subscript l = 1 is omitted for convenience, since the nozzle velocity is based on thermodynamic conditions at the inlet stage only. Differentiating Eq. (7.4-65) and rearranging gives,
where, from Eq. (7.4-55) and Eq. (7.4-58),
Now, introducing Eq. (7.4-67) into Eq. (7.4-66) and rewriting the differential change in flow in a finite change form yields,
where \Delta h is again given by Eq. (7.4-60) except that the subscript l should now be l - 1. Thus the discretization of the momentum equation results in, after inserting Eq. (7.4-60) into Eq. (7.4-68) and rearranging,
Similarly, \Delta h in Eq. (7.4-68) can also be expressed in an implicit form as described in Eq. (7.4-64). It is not surprising that \Delta P_{l} does not appear in Eq. (7.4-69), since the flow rate is affected by the volume pressure only at the previous stage as long as the flow is choked.
As can be seen in Eq. (7.4-47) to Eq. (7.4-49), the two‑phase choked flow between stages l = 1 and l is also dependent on thermodynamic conditions at the inlet turbine stage l = 1 only. For simplicity, the subscript l = 1 is not shown in the derivation of the equation for change in mass flow rate. It facilitates the derivation if Eq. (7.4-48) is rewritten in a simplified form, by carrying out the algebra in the equation, as,
where a = 9.325 \times 10^{-2} and b = 2.356 \times 10^{-4}. The flow rate in the nozzle now is just w = \rho V A with V given by Eq. (7.4-47). From the analogy between Eq. (7.4-46) and Eq. (7.4-47), the differential change in the two‑phase choked flow can be deduced readily from Eq. (7.4-66), which is for choked flow for steam, to be,
From Eq. (7.4-40), it is obvious that
where, since the saturation temperature is determined solely by the saturation pressure, dT can be rewritten as,
Combining Eq. (7.4-71), Eq. (7.4-72), and Eq. (7.4-73) and rearranging results in,
where
Since the specific volume in a two‑phase fluid is a function of pressure and quality, dv in Eq. (7.4-74) should be expressed as,
Substituting Eq. (7.4-75) into Eq. (7.4-74) gives the finite change in the nozzle flow
Finally, the discretized equation for two‑phase choked flow is reached by applying Eq. (7.4-60) to Eq. (7.4-76),
dT / dP in Eq. (7.4-77) is computed by introducing perturbations in the pressure in the following equation (Ref. 7-13),
where c_{1} = 0.426776 \times 10^{2}, c_{2} = -0.389270 \times 10^{4} and c_{3} = -0.948654 \times 10^{1} if 0.000611 \leq P \leq 12.33 MPa, or c_{1} = -0.387592 \times 10^{3}, c_{2} = -0.125875 \times 10^{5}, and c_{3} = -0.152578 \times 10^{2} if 12.33 \leq P < 22.1 MPa. Eq. (7.4-77) does not contain \Delta P_{l} as in the discretized equation for choked flow for steam, Eq. (7.4-69).
7.4.11. Relief Valve
A relief valve is part of the System Pressure Relief System used to relieve overpressure transients occurring during plant isolations and load rejections. The relief valves open rapidly (self‑actuated) during plant transients to discharge fluids to the environment or relief tanks and close following the transients so that normal operation can be resumed. Normally the relief valves are located on the main steam line piping, and each valve is piped through its own uniform diameter discharge line.
7.4.11.1. Model Description
Relief valves, like the other types of valves used in the balance of plant, are modeled as flow elements, since a relief valve primarily affects mass flow rate and pressure drop along a flow path and thus is best described through the momentum equation. The details of the relief valve model are dictated by the behavior of this type of valve. A relief valve is normally closed, opening very quickly when the pressure drop across the valve reaches a specified set pressure. The fractional valve opening area is related to the pressure drop across the valve by a hysteresis curve; the one used in the current model is shown in Figure 7.4.14. Valve flow area varies linearly from fully open at or above the accumulated pressure to partially closed to the fraction A(1) at the set pressure. The flow area then remains constant until the valve pressure drop is below the blowdown pressure, at which point the valve closes fully. The relief valve, therefore, behaves in many respects like a check valve. However, flow through the relief valve is normally choked and so must be modeled using a momentum equation such as the ones described in Section 7.4.10 for choked flow in the nozzle model. The relief valve is therefore modeled as a nozzle which can open and shut in much the same way as the check valve does.
In order to avoid the numerical instabilities which might be caused by the step changes in flow area shown at the blowdown and set pressures in Figure 7.4.14, the step changes are modified to linear changes of flow area as a function of pressure within a response time. This alteration of the ideal hysteresis curve of Figure 7.4.14 actually makes the model more realistic, since an actual relief valve exhibits a response time which is the maximum valve opening time (for example, 0.2 second). This response time is to be specified by the user as part of the valve input data.
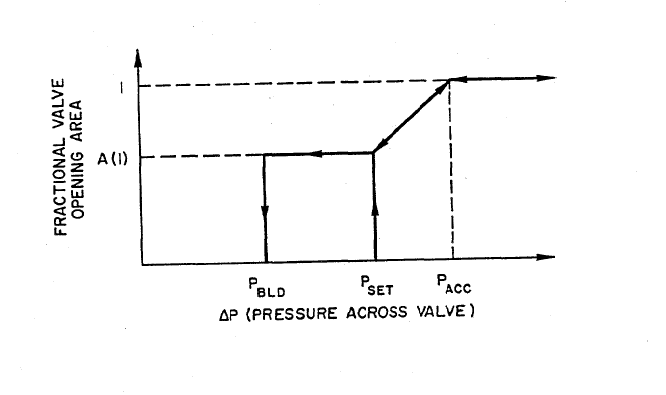
Figure 7.4.14 Simple Relief Valve Hysteresis Curve
In summary, the relief valve model consists of a modified check valve model and a modified nozzle model. The modified check valve model determines the fractional valve opening area, according to the hysteresis curve and the pressure difference across the relief valve, and then the modified nozzle model uses this flow area in calculating the flow rate through the relief valve.
The difference between the check valve model and the modified check valve model is that the check valve changes state (close or open) by adjusting the orifice coefficient in the incompressible flow momentum equation according to a user‑input table of orifice coefficients versus time, whereas the modified check valve model changes state by adjusting the fractional valve opening area to a user‑input value, in accordance with the hysteresis curve, within a user‑input response time. In fact, the orifice coefficient functions like an inverse fractional opening area, since the orifice coefficient is inversely proportional to the square of the flow rate through the check valve under a fixed pressure drop across the valve Eq. (7.2-24). The modified nozzle model differs from the nozzle model in that there is sometimes no flow through the nozzle (the relief valve) if the fractional valve opening area generated by the modified check valve model is zero, whereas the nozzle model always has a flow, either choked or nonchoked, between two stages.
7.4.11.2. Analytical Equations and Discretized Equations
All aspects discussed in Section 7.4.10.2 and Section 7.4.10.3 about the momentum equations for the nozzle model apply to the relief valve model. Two additional points to note are that 1) the work term H_{l} in Eq. (7.4-30) and Eq. (7.4-50) (included in Q_{l}) is removed when these two energy equations are used for the volume following the relief valve, since there is no work done by the flow through the valve and 2) when there is no flow through the valve, the pressure change in the volumes at either end of the relief valve will have no contributions from the momentum equation of the relief valve (as is easily seen in Eq. (7.4-61), Eq. (7.4-69), and Eq. (7.4-77) when w = 0).
7.4.12. Steady-State Initialization
The steady‑state initialization process takes the input data entered by the user and from the data computes the steady‑state parameters which characterize each component. The elements of the initialization process for the models discussed in this report can be separated into three groups: those for heater models, those for the turbine model, and those for the relief valve model. These three groups of calculations will now be discussed separately.
7.4.12.1. Steady‑State Initialization for the Heater Models
Some steady‑state parameters must be calculated for all heater models, both open and closed. These include:
compute the heater temperature from the equation of state,
determine the quality of the heater if the user inputs the two-phase interface and vice versa, by Eq. (7.4-5) or Eq. (7.4-8),
check the mass conservation from all of the inlet and outlet flows,
calculate the heat source term steady‑state value from the net energy entering the volume through the inlet and outlet flows,
introduce the pseudo heat conduction coefficient, to account for the minor energy imbalance resulting from inconsistencies between user‑specified thermodynamic conditions and the SASSYS-1 correlations for the thermodynamic properties, and
calculate the area‑weighted quality for the outlet flow, if the two‑phase interface intersects any of the outlet openings, from Eq. (7.4-2).
In addition, there are some calculations required only for the initialization of closed heaters. These include:
initialize the heat transfer coefficients, both on the tube side and on the shell side,
determine the calibration factor for the tube surface heat transfer area,
initialize the fluid enthalpy at each node on the tube side,
find the temperature distributions of the tube side fluid and the metal tube, and
include the heat transfer energy between the shell side fluid and the metal tube in the heat source term steady‑state value (item (4) above).
Furthermore, for those heaters which contain a drain and/or a desuperheating region, the following initialization is also performed for the shell side of the drain and/or the desuperheating region:
calculate the enthalpy from the equation of state,
initialize the heat transfer coefficient, from Eq. (7.4-10),
compute the heat source term steady‑state value from the net energy gain through the inlet and outlet flows, and
determine the calibration factor, separate from the one used for the shell side of the heater, for the tube surface heat transfer area to obtain a balance between the energy transfer through the tube boundary and the heat source term steady‑state value from item (14).
7.4.12.2. Steady‑State Initialization for the Turbine Model
The turbine model requires initialization of parameters both for each turbine stage and for each nozzle between stages. The job of the turbine stage steady‑state initializer is the following:
check the mass conservation from all of the in]et and outlet flows,
compute the steady‑state stage work, from Eq. (7.4-31),
calculate the turbine torque and set the generator torque equal to the turbine torque,
check the energy conservation (work balanced with the net energy in through flows), and
introduce a pseudo‑heat conduction coefficient to account for any minor energy imbalance within the stage.
The steady‑state nozzle initializer performs the following:
calibrate the nozzle area according to the user‑specified flow rate, using the mass flux calculated from Eq. (7.4-45) or Eq. (7.4-49), and
compute the isentropic enthalpy {\overline{h}}_{l}(P_{l},s_{l - 1}) and density {\overline{\rho}}_{l}(P_{l},{\overline{h}}_{l}).
7.4.12.3. Steady‑State Initialization for the Relief Valve Model
The steady‑state relief valve initializer does the following:
calibrate the valve flow area when the valve is fully open, according to the user‑specified relief valve capacity (since the relief valve is normally closed in the steady state), using the same equations for calculating the mass flux as are used in the nozzle model, and
set the flag to reflect the state of the relief valve as being on the upper section of the hysteresis curve in Figure 7.4.14, or on the lower section of the hysteresis curve.
7.4.13. Code Implementation and Operation
7.4.13.1. The Transient Solution Algorithm
This section describes the incorporation of the component models discussed in this section into the transient solution algorithm discussed in Section 7.2.6.2.
Perhaps the easiest way to document the revised transient solution algorithm is to start with the algorithm of Section 7.2.6.2. The original algorithm is broken up into eleven steps; some of these steps are affected by the addition of the heater, turbine, and relief valve models, and some steps are not. The modifications to the algorithm which are necessary to incorporate the additional models are as follows:
- Steps 1 and 2:
These involve only the steam generator and superheater models and thus are not affected by the additional models.
- Step 3:
The calculation of the matrix coefficients and source terms performed in this step must properly account for the enthalpy of fluid leaving any of the heater volumes, as discussed in Section 7.4.2.2, 7.4.7.2, and 7.4.8.2 of this report. Also, the heat source term Q_{l}^{n} should include the stage work term H_{l}^{n} for each stage of a turbine.
- Step 4:
The incompressible flow momentum equation for which the coefficients are computed in this step must be replaced by Eq. (7.4-61), Eq. (7.4-69), or Eq. (7.4-77) (the choice of equation being dependent upon flow conditions, as discussed in Section 7.4.10.3) in the case of a nozzle or relief valve.
- Steps 5 and 6:
These involve the mechanics of assembling and solving the matrix equation and so are not affected by the additional models.
- Step 7:
In addition to updating the volume pressures and the flows in incompressible flow segments, the flows in any nozzles or relief valves must be updated.
- Step 8:
In this step, the heat source terms for any of the heater models discussed in this report are updated. The temperature profiles of the tube side fluid and the metal tube are updated for any closed heaters, and the heater shell side temperature is also updated. In addition, the temperature, enthalpy, and heat source are updated in any drains or desuperheating regions. For any turbine stages, the work term, the turbine torque, and the rotor angular velocity are updated.
- Step 9:
Volume‑averaged densities and enthalpies are computed here, and this calculation does not change for the new models.
- Step 10:
In non‑heated flow segments, enthalpy transport is applied at this point to update the enthalpy distribution along each segment. In the heated elements within closed heaters, the fluid enthalpy at each node along the element is updated according to the energy equations discussed earlier. Flow segments which involve a combination of heated and non‑heated elements use enthalpy transport in all non‑heated elements and compute energy transfer within heated elements.
- Step 11:
Pump parameters and gravity heads are computed in this final step, and so this step is not affected by the additional models.
7.4.13.2. Code Operation
The calculation procedures described in Section 7.4.12 and Section 7.4.13.1 are implemented by the set of subroutines and functions listed in Table 7.2.1. Most subroutines with names beginning with SS (Steady State) are called from the steady‑state balance‑of‑plant driver SSBOP (the exception is subroutine SSRVW, which is called from subroutine RENUM, the balance‑of‑plant input data and nodalization routine). Subroutines with names beginning with TS (Transient State) are called from the driver subroutine WTRDRV.
The structure of the balance‑of‑plant coding, including the subroutines of Table 7.2.1, is shown in Figure 7.2.1 for the steady‑state coding and in Figure 7.2.2 for the transient coding.
As seen in Figure 7.2.1, the balance‑of‑plant operation starts with subroutine RENUM, which is called from the PRIMAR‑4 subroutine SSPRM4. SSPPM4 is an initialization subroutine which has been modified to call the balance‑of‑plant initialization subroutines also. Subroutine SSRVW is called by RENUM to calibrate the relief valve flow areas once the input data for each relief valve have been entered through RENUM. After the work is completed in RENUM, SSPRM4 calls SSBOP to execute the remainder of the steady-state balance‑of‑plant initialization. All the calculations necessary to complete the steady‑state initialization of the balance-of-plant components are done in SSBOP or in subroutines called by SSBOP. First, SSBOP calls the nozzle initializer, SSNZZL, to compute the isentropic enthalpies and the fluid densities following the isentropic expansion, and to adjust the nozzle areas. Next, SSBOP calls SSTRBN, the turbine initializer, to calculate the steady‑state turbine stage work, check mass and energy conservation, and initialize the turbine and generator torques. SSBOP then calls SSHTRW, the heater initializer, to compute the shell‑side temperatures and/or the tube-side temperature profile (along with the heat transfer area calibration factor), calculate the heat source terms (including heat source terms in the drain and/or the desuperheating region, if such regions are present), check mass and energy conservation, and find the pseudo‑heat conduction coefficient. SSBOP then goes on to call other initialization subroutines.
With the steady‑state initialization completed, the balance‑of‑plant transient calculation starts with subroutine TSBOP by a call from the PRIMAR‑4 subroutine STEPTM (see Figure 7.2.2). TSBOP is the driver for the entire waterside transient calculation, including the steam generator and superheater models. TSBOP is called once each PRIMAR‑4 timestep. After updating the balance‑of-plant standard valves (which operate on the PRIMAR‑4 timestep), TSBOP enters a loop that operates on the balance‑of‑plant timestep, which is generally smaller than the PRIMAR‑4 timestep and is never larger than the PRIMAR‑4 timestep. For each balance‑of‑plant timestep, TSBOP first calls the steam generator (and superheater, if any are present in the system) subroutines, then it calls WTRDRV, the driver subroutine for the remainder of the balance of plant. WTRDRV assembles the matrix equation for the compressible volume pressure changes, solves for the pressure changes, and updates the flow rates and the remaining balance‑of-plant parameters. In the process of assembling the matrix equation, WTRDRV must compute, for each flow segment, the contribution of each component in the segment (e.g., pipes, valves, pumps, etc.) to the segment momentum equation. These contributions are calculated, for the different component types, by the six subroutines grouped together in Figure 7.2.2, beginning with SGMOM and ending with TSRVW. The first four subroutines are discussed in Section 7.2; the remaining two are TSNZZL, which calculates the contribution for nozzles, and TSRVW, which calculates the contribution for relief valves. Once the matrix equation has been solved for the compressible volume pressure changes, TSNZZL and TSRVW are called again to update nozzle flow rates and relief valve flow rates, respectively. Since relief valves are normally closed, TSRVW checks to find out first if the relief valve is open, to decide whether to proceed with the generation of the momentum equation coefficients or simply to bypass the calculation if the valve is closed. In updating the relief valve flow, subroutine TSRVW calls REVLW to obtain the new valve flow area and then calculates the new valve flow rate; again, TSRVW will skip the computation of the new flow rate and set the new flow rate to zero if the new valve flow area is found to be zero.
WTRDRV moves on to call TSTRBN, which updates the turbine stage work and the turbine torque. Next, WTRDRV calls TSHTRW, which executes most calculations related to heaters, other than those simulated by the simple heater model in Section 7.2. Subroutine TSHTRW updates the shell‑side temperature and/or the tube‑side temperature profile and also the heat source terms (including the heat source terms in the drain and/or desuperheating regions, if such regions are present). After these calls, the enthalpy transport calculation along unheated flow elements is performed by a call to TRNSPT, which will also account for enthalpy transport in flow paths following heated elements within heaters. Subroutine ARF is then called, as necessary, to determine the new two‑phase interface in heaters configured as cylinders lying on the side.
Once WTRDRV has returned control to TSBOP, the balance‑of‑plant timestep is updated and TSBOP performs another series of calls to the steam generator and superheater subroutines and to WTRDRV, until the end of the PRIMAR‑4 timestep is reached. TSBOP then goes on to perform I/O tasks, then returns control to STEPTM.