7.3. Steam Generator Model

7.3.1. Once-Through Steam Generator

In an once‑through steam generator subcooled feedwater enters the bottom on the water side and superheated steam comes out the top (see Figure 7.3.1). Considering that there is a transition boiling zone, the water side is naturally divided into three regions. Figure 7.3.2 shows a detailed schematic of the once‑through steam generator. The top of the subcooled zone and the bottom of the boiling zone is defined by the point of saturated liquid enthalpy. The top of the boiling zone and the bottom of the superheated vapor zone is defined by the point of saturated vapor enthalpy. This is the situation during normal steady‑state operation. Various transient conditions can produce any situation from a steam generator filled with subcooled water to total dry‑out on the water side. The current model can calculate this whole spectrum of conditions with one proviso: there must always be a subcooled liquid region of some finite length at the inlet of the steam generator; but this length can be extremely small. Another way of stating this assumption is that there is no provision for two‑phase fluid or superheated vapor in the inlet plenum of the steam generator. Going to the other end of the spectrum of transient cases, the complete disappearance of both the boiling and superheated vapor zones can be calculated. If, however, there is a superheated vapor zone, there must, of course, be a boiling zone. Each of the three zones, therefore, is treated as a separate calculation with its own node structure and providing boundary conditions for the adjacent region or regions even as each zone length changes during the transient.

The steam generator is, of course, one module in the balance‑of‑plant sequence. As far as the system is concerned, it represents a pressure drop and a momentum source or sink from a hydrodynamic point of view. The balance-of‑plant calculation produces pressures at the inlet and outlet plena of the steam generator as well as the mass flow into the steam generator. As will be shown later, the steam generator model itself calculates outlet flows from the steam generator. The steam generator provides the balance‑of‑plant momentum equation with an estimate of the pressure drop across the steam generator. This will be discussed later.

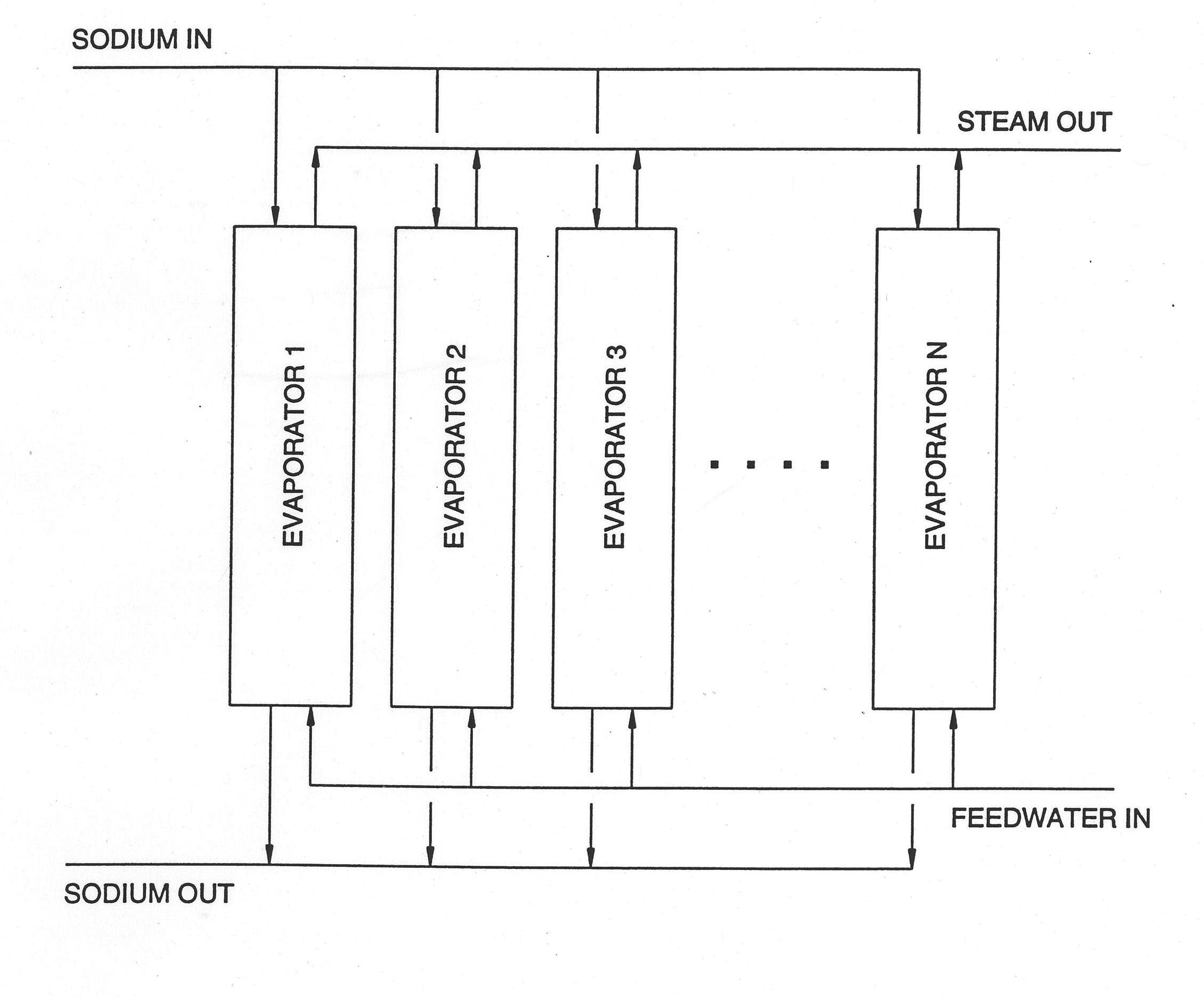
Figure 7.3.1 Once-Through Steam Generator

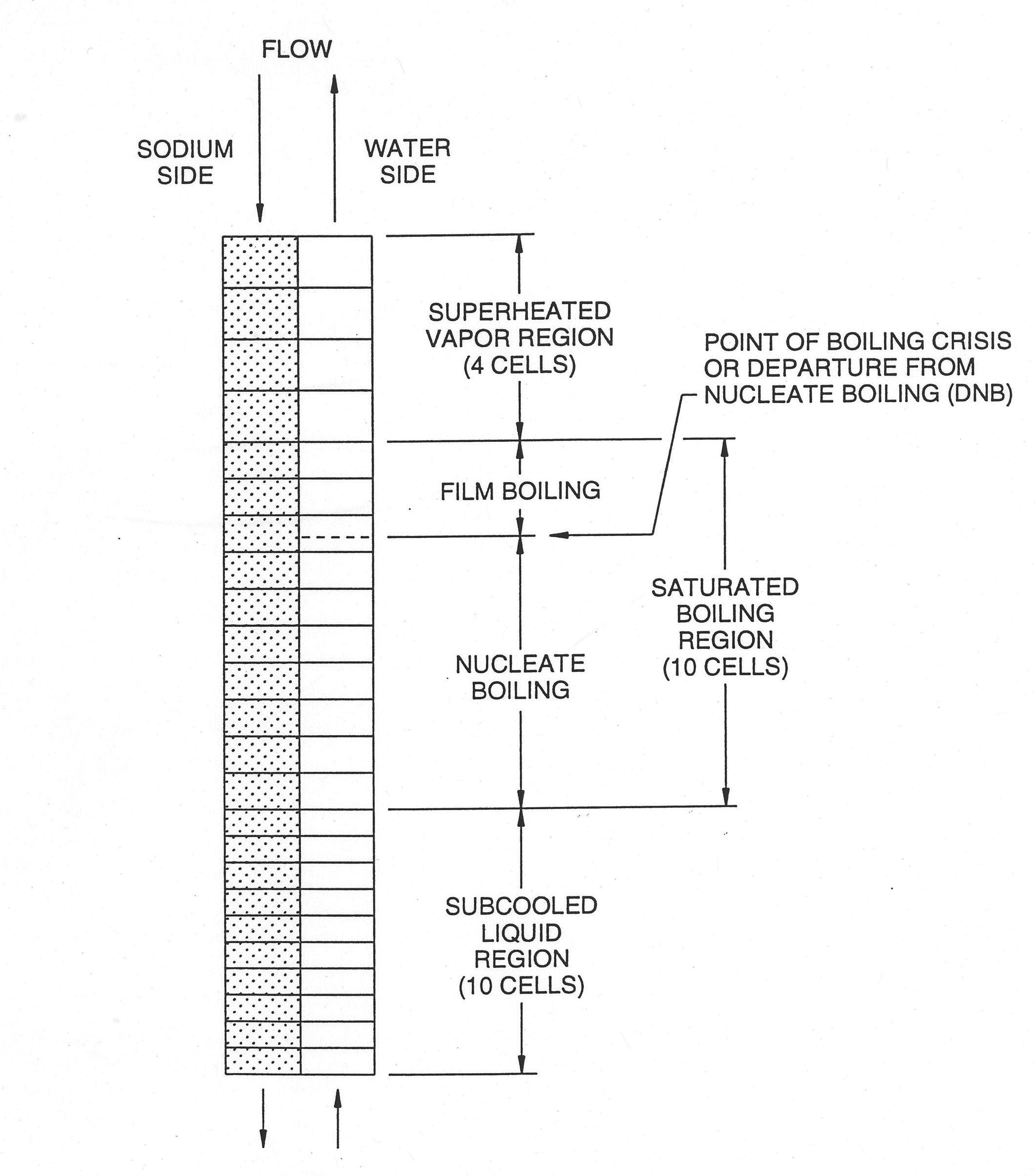
Figure 7.3.2 Schematic of Once-Through Steam Generator

There are two main points to emphasize here, however. First, the inlet and outlet pressures provided by the balance‑of‑plant momentum equation are simply averaged and this average pressure is used at each time step by the steam generator to calculate properties. Thus no account is taken of the variation of pressure across the steam generator for the purpose of calculating properties. For many and probably most transient calculations of interest, this pressure variation is small and, although not trivial, can be safely neglected in the total context of the calculation. There are some transients, however, involving large pressure reductions downstream of the steam generator, which would produce a significant pressure variation across the steam generator, the neglect of which could lead to some level of inaccuracy.

The second point to emphasize is, given the estimate of the pressure drop across the steam generator, the inlet flow is provided as a boundary condition for the steam generator. There is no momentum equation coupled to the mass and energy conservation equations which characterize the regions in the steam generator to produce velocities. Instead the mass flows above the subcooled zone result from the mass and energy equations alone (as shown below), given the inlet flow as a driving function.

The subcooled liquid and superheated vapor zones each have their own heat transfer regime. The boiling zone has two heat transfer regimes separated at the boiling crisis or departure‑from‑nucleate‑boiling (DNB) point. No smoothing or intermediate regimes are used between these four regimes. This provides of course calculation convenience. Heat transfer phenomena in a steam generator are much more complicated. The adequacy of this heat transfer scheme will be judged by benchmarking against experimental data. The DNB point is crucial to properly characterizing the boiling zone. But tracking the point produces calculation difficulties. This will be explained in some detail later. Suffice it to say here that the DNB point is assumed to be at the intersection of two curves, one representing the local heat flux at the tube wall and the other representing the heat flux required for the boiling crisis to occur. In this way, the point of maximum boiling heat flux is tracked. This DNB point is tracked continuously within the node structure of the boiling zone and the heat flux in the cell where the DNB point is a prorated average of the two boiling heat transfer regimes since the volumetric heat flux is always calculated on a cell‑average basis. Depending on the fineness of the node structure, this produces some amount of inaccuracy and approximation to the real physical situation.

The following are general forms of the continuity and of the enthalpy form of the energy conservation equation in one dimension:

(7.3-1)\[\frac{\partial\rho}{\partial t} = - \frac{\partial G}{\partial z}\]

(7.3-2)\[\frac{\partial(\rho h)}{\partial t} = - \frac{\partial\left( Gh \right)}{\partial z} + Q - \left( \tau:\nabla v \right) + \frac{\partial P}{\partial t} + v\frac{\partial P}{\partial z}\]

\(Q\) is a volumetric heat source, \(- \left( \tau:\nabla v \right)\) represents viscous dissipation and \(v(\partial P/\partial z)\) is a work‑energy conversion term (representing feedwater pump work, for example). The viscous dissipation term will be dropped for this application because it is small compared to other terms. The work term will also be neglected for the same reason although it is possible that in certain extreme conditions the term could be of some significance. The general energy equation thus becomes,

(7.3-3)\[\frac{\partial(\rho h)}{\partial t} = - \frac{\partial\left( Gh \right)}{\partial z} + Q + \frac{\partial P}{\partial t}\]

Incompressible flow is assumed in the subcooled liquid zone. The balance‑of‑plant momentum equation provides the inlet mass flow, as stated above and thus the mass flow for the whole zone \(\left( \Delta G = 0 \right)\). Therefore no continuity equation is needed to characterize the region. The enthalpy level and shape and the subcooled region length are all that need be solved for with a coupled set of nodal energy conservation equations. The boundary conditions for flow are the constant mass flow and for energy, the inlet enthalpy and the saturated liquid enthalpy unless the zone reaches the top of the steam generator in which case the region length is known and the outlet enthalpy is calculated. Since is assumed to be zero, the LHS of the energy equation, Eq. (7.3-3), can be simplified. The density changes over the transient as a result of changes in pressure and enthalpy but these changes are taken into account by updating the density at the end of each time step in the transient after new enthalpies and pressures are obtained.

In the boiling region, compressible flow is calculated with sets of nodal mass and energy conservation equations. The equations are formulated in terms of the void fraction instead of density and enthalpy. This is conveniently done since saturation conditions are always assumed and a no slip condition between phases is assumed; and also because saturation properties are functions of pressure alone. Thus simultaneous nodal continuity and energy equations are used to solve for mass flows and void fractions. The boundary conditions at the bottom of the zone are the single‑phase liquid flow and the saturated liquid enthalpy (i.e. void fraction zero). At the top of the zone, there is either the saturated vapor enthalpy (i.e. void fraction 1.0) or, if the boiling zone extends all the way to the top of the steam generator, then the void fraction is a free variable and only lower boundary conditions are required. When the zone does not extend to the top of the steam generator, then the upper boundary condition of the saturated vapor enthalpy is used by requiring that the length of the zone be adjusted until the upper boundary condition is satisfied.

Compressible flow is also assumed in the superheated vapor region. The boundary conditions at the bottom of the zone are the saturated vapor enthalpy and the mass flow calculated at the top of the boiling zone. Since the length of the zone is known, simultaneous nodal mass and energy equations are used to solve for enthalpies and mass flows all the way to the top of the steam generator.

On the sodium side, there is no change of phase and consequently the liquid can be adequately treated with incompressible flow. There is a calculation of the sodium flow external to the steam generator calculation so that, as far as the steam generator is concerned, the mass flow is given. Therefore no continuity equation is required. Besides the mass flow, the only boundary condition required is the inlet sodium temperature at the top of the steam generator. Only the nodal energy equation is required to solve for the enthalpy shape on the sodium side. In addition, given the relatively stable and low pressure conditions on the sodium side, the pressure term in the energy equation Eq. (7.3-3) can be safely neglected.

The heat capacity of the tube wall separating the water and the sodium must be taken into account. Therefore its effect on the heat transfer from the sodium to the water is treated by means of a wall temperature calculation. With no convective or pressure terms the energy equation Eq. (7.3-3) becomes much simplified. Also, the density is assumed to be temperature independent which further facilitates the solution.

7.3.2. Recirculation-Type Steam Generator

Figure 7.3.3 depicts a steam generator which consists of several evaporators, several superheaters, a steam drum and a recirculation loop. Subcooled water is pumped into the bottom of the evaporator. Within the evaporator the water boils and a two‑phase fluid, typically of very high quality, leaves the top of the evaporator and enters the steam drum. One exit line from the steam drum transports saturated steam to the bottom of the superheater where more heat is added so that highly superheated steam leaves the top available for the turbines. The other exit line from the steam drum transports saturated liquid to the pump but before reaching the pump it is mixed with feedwater. This mixture is substantially subcooled, therefore, and is pumped back to the evaporator to complete the cycle.

The modeling of the evaporator can be done with the once‑through steam generator model which is designed to model any situation from a liquid‑filled steam generator to the normal operating condition for a once‑through type with superheated vapor exiting the top. Thus the physical modeling assumptions of the previous section apply to the evaporator.

The modeling of the superheater is different, however, than the super-heated vapor zone of the previous section. Without elaborating on the details, it is sufficient here to say that the momentum equation of the balance‑of‑plant model is much more tractable if the assumption of incompressible flow is made for the superheater. Since the superheater operates at quite high pressures, this incompressibility assumption is probably adequate in most transient conditions. There may, however, be certain conditions when the pressure in the superheater is greatly reduced when inaccuracies may result from this assumption. A study of this effect would have to be undertaken to decide the issue and it has not been done so far. The lower boundary condition besides the given mass flow is the inlet enthalpy (i.e. the saturated vapor enthalpy). Thus the enthalpy shape is determined given these conditions. The density is updated each time step during the transient after new enthalpies and pressures have been determined.

The steam drum is modeled as a zero‑dimensional reservoir in the sense that perfect mixing of all incoming fluid and the pre‑existing separated two phases is presumed. There is one proviso here, however: the liquid level must be tracked so that appropriate action can be taken when liquid may enter the pipe to the superheater or vapor may enter the pipe to the recirculation pump.

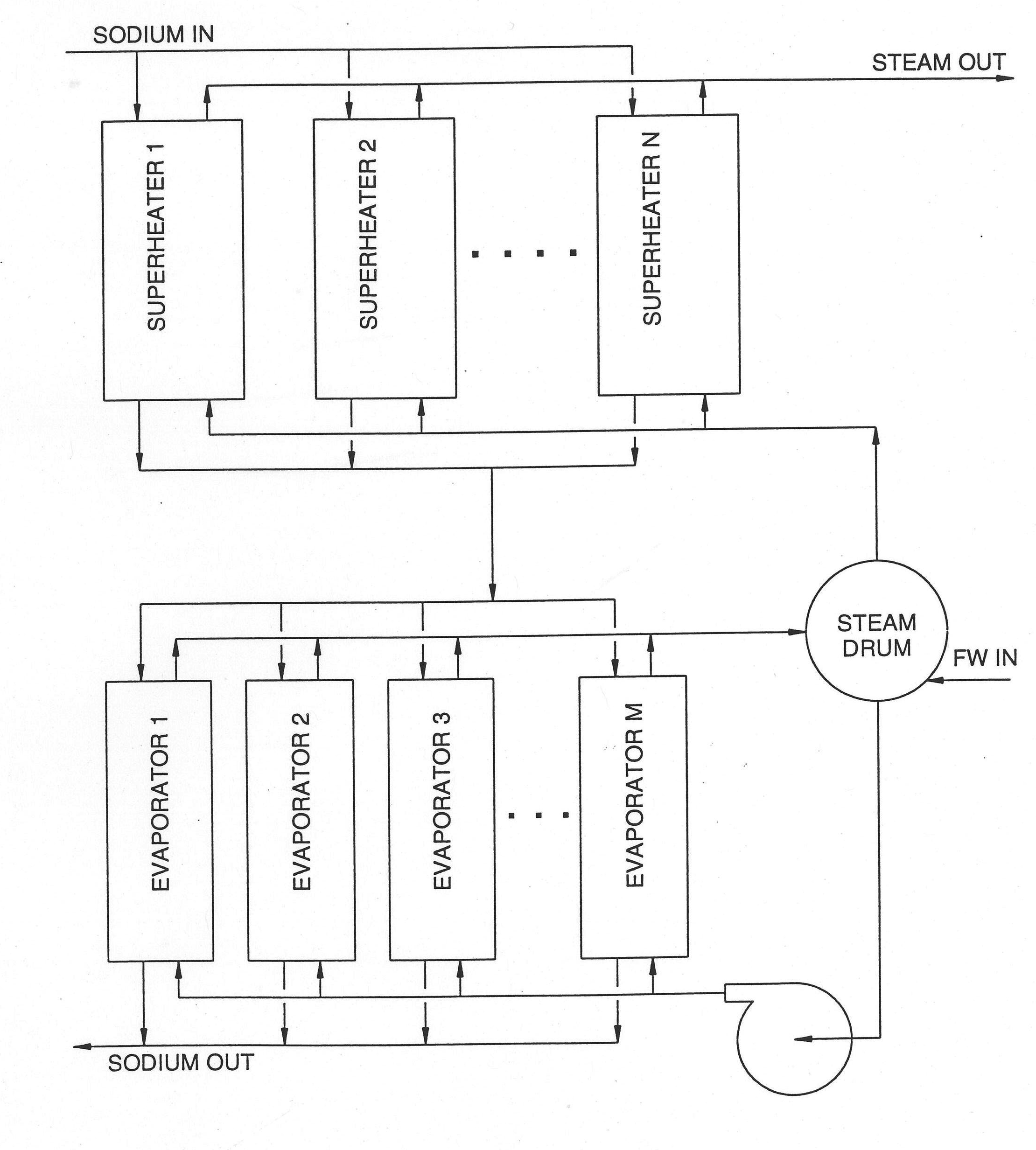
Figure 7.3.3 Steam Generator with Separate Evaporator and Superheaters and Recirculation Loop

7.3.3. Numerical Solution Methods

7.3.3.1. Once‑Through Steam Generator

7.3.3.1.1. General Forms of the Conservation Equations

Before the individual solution methods for each water side region and the sodium side can be considered, general forms of the continuity and energy equations must be developed. Equations will be given for one node of the multi‑node system of equations. Integration of the continuity Eq. (7.3-1) over the length of one cell from \(Z_{i}\) to \(Z_{i + 1}\) gives,

(7.3-4)\[\int_{Z_{i}}^{Z_{i + 1}} \frac{\partial}{\partial t} \rho dz = - \int_{Z_{i}}^{Z_{i+1}} \frac{\partial}{\partial z} G dz\]

According to Leibnitz’s Theorem,

(7.3-5)\[\int_{Z_{i}}^{Z_{i+1}} \frac{\partial}{\partial z} \rho dz = \frac{d}{dz} \int_{Z_{i}}^{Z_{i+1}} \rho dz - \rho_{i + 1} \dot{Z}_{i + 1} + \rho _{i} \dot{Z}_{i}\]

Eq. (7.3-4) becomes,

(7.3-6)\[\frac{d}{dt} \int_{Z_{i}}^{Z_{i + 1}} \rho dz - \rho_{i + 1} \dot{Z}_{i + 1} + \rho_{i} \dot{Z}_{i} = -\int_{Z_{i}}^{Z_{i + 1}} \frac{\partial}{\partial z} G dz\]

Therefore,

(7.3-7)\[\frac{d}{dt}\left\{ \overline{\rho}_i {\Delta}Z_{i} \right\} - \rho_{i + 1}{\dot{Z}}_{i + 1} + \rho_{i}{\dot{Z}}_{i} = - {\Delta}G_{i}\]

Donor‑cell differencing is used to enhance numerical stability. In order to write the equation in donor‑cell form, let \(\rho_{i + 1}\) replace the average value over the interval, \(\overline{\rho}_{i}\) and simplify,

(7.3-8)\[\dot{\rho}_{i + 1} \Delta Z_{i} - \Delta \rho_{i} \dot{Z}_{i} = - \Delta G_{i}\]

Integration of the enthalpy form of the energy Eq. (7.3-3) from \(Z_{i}\) to \(Z_{i + 1}\) gives,

(7.3-9)\[\int_{Z_{i}}^{Z_{i + 1}} \frac{\partial}{\partial t} \left( \rho h \right) dz = - \int_{Z_{i}}^{Z_{i + 1}} \frac{\partial}{\partial z} \left( G h \right) dz + \int_{Z_{i}}^{Z_{i + 1}} Q dz + \int_{Z_{i}}^{Z_{i + 1}} \frac{\partial}{\partial z} P dz\]

According to Leibnitz’s theorem,

(7.3-10)\[\int_{Z_{i}}^{Z_{i + 1}}{\frac{\partial}{\partial t}(\rho h)dz} = \frac{d}{dt}\int_{Z_{i}}^{Z_{i + 1}}{(\rho h)dz} - {(\rho h)}_{i + 1}{\dot{Z}}_{i + 1} + {(\rho h)}_{i}{\dot{Z}}_{i}\]

(7.3-11)\[\int_{Z_{i}}^{Z_{i + 1}} \frac{\partial}{\partial t} P dz = \frac{d}{dt} \int_{Z_{i}}^{Z_{i + 1}} P dz - P_{i + 1} \dot{Z}_{i + 1} + P_{i} \dot{Z}_{i}\]

Eq. (7.3-9) becomes

(7.3-12)\[\begin{split}\frac{d}{dh} \int_{Z_{i}}^{Z_{i+1}} \left( \rho h \right) dz - \left( \rho h \right)_{i + 1} \dot{Z}_{i + 1} + \left( \rho h \right)_{i} \dot{Z}_{i} = - \int_{Z_{i}}^{Z_{i+1}} \frac{\partial}{\partial z} \left( G h \right) dz + \int_{Z_{i}}^{Z_{i+1}} Q dz \\ + \frac{d}{dt} \int_{Z_{i}}^{Z_{i+1}} P dz - P_{i + 1} \dot{Z}_{i + 1} + P_{i} \dot{Z}_{i}\end{split}\]

Therefore,

(7.3-13)\[\begin{split}\frac{d}{dt} \left\{ \left( \overline{ \rho h } \right)_{i} \Delta Z_{i} \right\} - \left( \rho h \right)_{i + 1} \dot{Z}_{i + 1} + \left( \rho h_{i} \right) \dot{Z}_{i} = - \Delta \left( G h \right)_{i} + Q_{i} \Delta Z_{i} \\ + \frac{d}{dt} \left\{ \overline{P}_{i} \Delta Z_{i} \right\} - P_{i + 1} \dot{Z}_{i + 1} + P_{i} \dot{Z}_{i}\end{split}\]

In order to write Eq. (7.3-13) in donor‑cell form, let \(\left( \rho h \right)_{i + 1}\) replace the average value over the interval \(\left[ \rho h \right]_{i}\) let \(P_{i + 1}\) replace \(\overline{P}_{i}\), and simplify,

(7.3-14)\[\left( \rho \dot{h} \right)_{i + 1} \Delta Z_{i} - \Delta \left( \rho h \right)_{i} \dot{Z}_{i} = -\Delta \left( G h \right)_{i} + Q_{i} \Delta Z_{i} + \dot{P}_{i + 1} \Delta Z_{i} - \Delta P_{i} \dot{Z}_{i}\]

As discussed before, the pressure variation across the steam generator is neglected, i.e., \(\Delta P_{i} = 0\), and Eq. (7.3-14) becomes

(7.3-15)\[\left( \rho \dot{h} \right)_{i + 1} \Delta Z_{i} - \Delta \left( \rho h \right)_{i} \dot{Z}_{i} = -\Delta \left( G h \right)_{i} + Q_{i} \Delta Z_{i} + \dot{P} \Delta Z_{i}\]

Each of the three regions on the water side is divided into a fixed number of cells. Since the region lengths vary during the transient, the cell lengths also vary and are thus a constant fraction of the varying region length. Thus \(\Delta Z_{i} = \frac{1}{n} Z_{x}\) where \(Z_{x}\) is the current length of region \(x\) and \(n\) is the number of cells in region \(x\). Therefore the subscript \(i\) can be dropped for \(\Delta Z_{i}\) in equations for a given region. On the sodium side, the same node structure is used as on the water side in order to simplify the calculation, although the precise node structure on the sodium side is not nearly as important as on the water side since there is no change of phase and properties thus calculated parameters change gradually and smoothly over the length of the steam generator.

All spatially variable parameters except two are evaluated at the cell boundary so that there are \(n+1\) values needed to characterize a region, where \(n\) is the number of cells in the region. The two exceptions are the tube wall enthalpy and the heat flux. The volumetric heat source is most conveniently calculated on a cell‑average basis so that n cells exactly encompass the whole of the heat transfer for a given region. If the heat source were calculated at the cell edge, then half‑cells would have to be used at the ends of a region where the heat transfer coefficients change form. In order to calculate the temperature gradients for the heat flux, linear averages over the cell length are computed from the cell‑edge values for water and sodium. However, there is no need to calculate the tube wall temperature at the cell edge and a cell‑centered value is most convenient for the heat flux calculation. Other parameters such as enthalpies, void fractions, mass fluxes, etc. are most conveniently calculated at the cell‑edge since this is where the boundary conditions are defined.

7.3.3.1.2. Subcooled Liquid Region

In the subcooled region, the mass flow is assumed to be uniform throughout the zone due to incompressible flow. Each time step during the transient an updated inlet mass flow is provided to the steam generator from the explicitly‑coupled momentum equation. Therefore no continuity equation is required. The coupled set of nodal energy conservation equations are used to determine the length of the zone and the nodal enthalpies simultaneously using the inlet enthalpy and the saturated liquid enthalpy as boundary conditions. Or, alternatively, when liquid fills the steam generator and the zone length is known, the outlet enthalpy is instead determined.

Using Eq. (7.3-15) and setting \(\dot{ \rho} = 0\) because of the incompressible flow, and recalling that \(\Delta Z_{i}\) is invarient within a zone, the following results for node \(i\),

(7.3-16)\[\dot{h}_{i + 1} \rho_{i + 1} \Delta Z - \Delta \left( \rho h \right)_{i} \dot{Z}_{i} = - \Delta \left( G h \right)_{i} + Q_{i} \Delta Z + \dot{P} \Delta Z\]

The following is Eq. (7.3-16) in finite difference form,

(7.3-17)\[\begin{split}h_{i + 1}^{k + 1} \frac{1}{\Delta t} \rho_{i + 1}^{k} \frac{1}{n} Z_{SC}^{k} - h_{i + 1}^{k} \frac{1}{\Delta t} \rho_{i + 1}^{k} \frac{1}{n} Z_{SC}^{k + 1} - \overline{\rho}_{i}^{k} \left(h_{i + 1}^{k} - h_{i}^{k} \right) \frac{i - 1}{n} \\ \times \frac{1}{\Delta t} \left(Z_{SC}^{k + 1} - Z_{SC}^{k} \right) = - G^{k + 1} \left(h_{i + 1}^{k + 1} - h_{i}^{k + 1} \right) + Q_{i}^{k} \frac{1}{n} Z_{SC}^{k + 1} + \dot{P} \frac{1}{n} Z_{SC}^{k + 1}\end{split}\]

There are several points to note concerning Eq. (7.3-17). The \(\Delta Z\) in the first term on the LHS is treated semi-implicitly in time since \(h_{i + 1}^{k + 1}\) is multiplied by \(Z_{SC}^{k}\), the value at the beginning of the time step and \(h_{i + 1}^{k + 1}\) is multiplied by \(Z_{SC}^{k + 1}\), the value at the end‑of‑step which needs to be determined. \(h_{i + 1}^{k + 1}\) cannot be multiplied by the end‑of‑step value without making the equation set non‑linear. Making the term semi‑implicit as opposed to fully explicit has been found to enhance stability in the calculation. The next point is that the density is entirely explicit in time. It is updated at the end of every time step as enthalpy and pressure change. This is consistent with the assumption of incompressibility as density changes slowly and gradually over time. Note also the use of \({\overline{\rho}}_{i}^{k}\) in the third term on the LHS of Eq. (7.3-17). \(\Delta \rho h_{i}\) becomes \(\rho \Delta h_{i}\) in order to preserve the proper sign of the term. Using \(\overline{\rho}_{i}^{k}\) which is \(0.5 \left( \rho_{i + 1}^{k} + \rho_{i}^{k} \right)\), introduces only a small error so long as the mesh structure is not too coarse. \(\Delta h_{i}\) must be explicit in time because it is multiplied by \(Z_{SC}^{k + 1}\) and the equation must be kept linear. \(G^{k + 1}\) in the convective term implies that the inlet mass flow is updated before the steam generator solution begins. The volumetric heat source is totally explicit since the temperatures used in calculating the \(\Delta T\) and the properties contained in the heat transfer correlation (see Section 7.7.2) cannot be made implicit without making the equation insoluble.

Rearranging Eq. (7.3-17) according to coefficients there are \(n\) equations of the following form,

(7.3-18)\[\begin{split}\left[-G^{k + 1} \right] h_{i}^{k + 1} + \left[ \frac{1}{\Delta t} \rho_{i + 1}^{k} \frac{1}{n} Z_{SC}^{k} + G^{k + 1} \right] h_{i + 1}^{k + 1} \\ + \left[ -h_{i + 1}^{k} \frac{1}{\Delta t} \rho_{i + 1}^{k} \frac{1}{n} - \overline{\rho}_{i}^{k} \left( h_{i + 1}^{k} - h_{i}^{k} \right) \frac{i - 1}{n} \frac{1}{\Delta t} - Q_{i}^{k} \frac{1}{n} - \dot{P} \frac{1}{n} \right] Z_{SC}^{k + 1} \\ = - \overline{\rho}_{i}^{k} \left(h_{i + 1}^{k} - h_{i}^{k} \right) \frac{i - 1}{n} \frac{1}{\Delta t} Z_{SC}^{k + 1}\end{split}\]

Eq. (7.3-18) can be written as,

(7.3-19)\[a_{i}h_{i} + b_{i}h_{i + 1} + c_{i} Z_{SC} = d_{i}\]

In the case where the liquid region does not reach the top of the steam generator, \(h_{1}\) and \(h_{n + 1}\) are known, since they are the inlet enthalpy and \(h_{f}. h_{2} - h_{n}\) and \(Z_{SC}\) are unknown (\(n\) unknowns) and are solved for as follows. (The superscript \(k + 1\) is dropped as unnecessary.)

From the first equation of the equation set Eq. (7.3-19), solve for \(h_{2}\), then for \(h_{3}\) from the second equation and so on,

(7.3-20)\[ \begin{align}\begin{aligned}h_{2} &= e_{1} + f_{1} Z_{SC}; & e_{1} &= \frac{d_{1} - a_{1} h_{1}}{b_{1}}, & f_{1} &= -\frac{c_{1}}{b_{1}}\\h_{3} &= e_{2} + f_{2} Z_{SC}; & e_{2} &= \frac{d_{2} - a_{2} e_{1}}{b_{2}}, & f_{2} &= -\frac{c_{2} + a_{2} f_{1}}{b_{2}}\\h_{i + 1} &= e_{i} + f_{i} Z_{SC}; & e_{i} &= \frac{d_{i} - a_{i} e_{i - 1}}{b_{i}}, & f_{i} &= - \frac{c_{i} + a_{i} f_{i - 1}}{b_{i}}\end{aligned}\end{align} \]

Finally, in the equation for \(h_{n + 1}, Z_{SC}\) can be solved for since \(h_{n + 1}\) is known. Then each of \(h_{2} - h_{n}\) can be solved for since they are all functions of only \(Z_{SC}\) in the equation set Eq. (7.3-20).

If the steam generator is filled with liquid, then the outlet enthalpy is unknown and there are \(n`s equations with :math:`h_{2} - h_{n + 1}\) as the unknowns. Eq. (7.3-16) becomes the following in finite difference form (the zone length, now constant as the length of the steam generator, is denoted simply as \(Z_{SC}\)),

(7.3-21)\[\frac{1}{\Delta t} \rho_{i + 1}^{k} \frac{1}{n} Z_{SC} \left(h_{i + 1}^{k + 1} - h_{i + 1}^{k} \right) = - G^{k + 1} \left(h_{i + 1}^{k + 1} - h_{i}^{k + 1} \right) + \frac{1}{n} Z_{SC} \left(Q_{i}^{k} + \dot{P} \right)\]

The following equations are simply solved from the bottom to the top of the steam generator successively,

(7.3-22)\[h_{i + 1}^{k + 1} = \frac{ \frac{1}{\Delta t} h_{i + 1}^{k} \rho_{i + 1}^{k} \frac{1}{n} Z_{SC} + G^{k + 1} h_{i}^{k + 1} + Q_{i} \frac{1}{n} Z_{SC} + \dot{P} \frac{1}{n} Z_{SC}}{\frac{1}{\Delta t} \rho_{i + 1}^{k} \frac{1}{n} Z_{SC} + G^{k + 1}}\]

7.3.3.1.3. Boiling Region

In the boiling zone, the fluid is treated as compressible. Simultaneous nodal equations are solved for void fraction, mass flow and region length. Boundary conditions are the saturated liquid enthalpy and subcooled region mass flow at the bottom of the boiling zone and either the saturated vapor enthalpy at the top of the zone or, if there is no superheated vapor zone, the region length is defined and the outlet enthalpy is determined. Only the pressure and the volumetric heat source are treated explicitly in time. The void fraction, the mass flow and the region length are all treated in fully implicit fashion. An iterative method is used to solve for the region length. The current value of the region length is held constant for each pass in the iteration while nodal void fractions and mass flows are calculated from the mass and energy equations. When the uppermost void fraction in the boiling zone is computed at the end of an iteration, its value is compared to 1.0 and the region length is adjusted appropriately and the iterative process continues until convergence. When the boiling zone extends to the top of the steam generator, the same method is used but there is no iteration since the region length is known.

First, a number of definitions and identities concerning a two‑phase fluid must be reviewed. \(\rho_{f}\) and \(h_{f}\) are the saturated liquid density and enthalpy respectively. \(\rho_{g}\) and \(h_{g}\) are the saturated vapor density and enthalpy. \(\rho_{fg} = \rho_g - \rho_f. h_{fg} = h_g - h_f\) The density of the two‑phase mixture is, with \(\alpha\) denoting the void fraction,

(7.3-23)\[\rho = \alpha \rho_{fg} + \rho_{f}\]

The enthalpy of the two‑phase mixture is, with \(\chi\) denoting the quality,

(7.3-24)\[h = \chi h_{fg} + h_{f}\]

Since homogeneous flow is assumed in the two‑phase zone,

(7.3-25)\[\chi = \frac{\alpha\rho_{g}}{\rho} = \frac{\alpha\rho_{g}}{\rho_{f} + \alpha\rho_{fg}}\]

Defining \(\left(h \rho \right)_{fg}\) as \(h_{g}\rho_{g} - h_{f}\rho_{f}\), Eq. (7.3-23), Eq. (7.3-24), and Eq. (7.3-25) imply,

(7.3-26)\[\left( h \rho \right) = h_{f} \rho_{f} + \alpha \left(h \rho \right)_{fg}\]

The general continuity Eq. (7.3-8) is written in terms of the nodal void fraction, \(\alpha\),

(7.3-27)\[\left( \dot{\alpha}_{i + 1} \rho_{fg} + \alpha_{i + 1} \dot{\rho}_{fg} + \dot{\rho}_{f} \right) \Delta Z - \left(\alpha_{i + 1} - \alpha_{i} \right) \rho_{fg} \dot{Z}_{i} = -\Delta G_{i}\]

The finite difference form of Eq. (7.3-27) is,

(7.3-28)\[\begin{split}\left[ \frac{1}{\Delta t} \left(\alpha_{i + 1}^{k + 1} - \alpha_{i + 1}^{k} \right) \rho_{fg}^{k} + \alpha_{i + 1}^{k + 1} \dot{\rho}_{fg}^{k} + \dot{\rho}_{f}^{k} \right] \frac{1}{n} Z_{TP}^{k + 1} \\ - \left(\alpha_{i + 1}^{k + 1} - \alpha_{i}^{k + 1} \right) \rho_{fg}^{k} \left[ \frac{i - j}{n} \frac{1}{\Delta t} \left( Z_{TP}^{k + 1} - Z_{TP}^{k} \right) + \dot{Z}_{SC} \right] = - \left(G_{i + 1}^{k + 1} - G_{i}^{k + 1} \right)\end{split}\]

Rearranging Eq. (7.3-28) according to coefficients of \(\alpha_{i + 1}^{k + 1}\) and \(G_{i + 1}^{k + 1}\) the following results,

(7.3-29)\[\begin{split}\left\{ \frac{1}{\Delta t} \rho_{fg}^{k} \frac{1}{n} Z_{TP}^{k + 1} + \dot{\rho}_{fg}^{k} \frac{1}{n} Z_{TP}^{k + 1} - \rho_{fg}^{k} \left[ \frac{i - j}{n} \frac{1}{\Delta t} \left(Z_{TP}^{k + 1} - Z_{TP}^{k} \right) + \dot{Z}_{SC} \right] \right\} \alpha_{i + 1}^{k + 1} \\ + G_{i + 1}^{k + 1} + \bigg\{ -\frac{1}{\Delta t} \alpha_{i + 1}^{k} \rho_{fg}^{k} \frac{1}{n} Z_{TP}^{k + 1} + \dot{\rho}_{f}^{k} \frac{1}{n} Z_{TP}^{k + 1} + \alpha_{i}^{k + 1} \rho_{fg}^{k} \bigg[ \frac{i - j}{n} \frac{1}{\Delta t} \\ \times \left(Z_{TP}^{k + 1} - Z_{TP}^{k} \right) + \dot{Z}_{SC} \bigg] - G_{i}^{k + 1} \bigg\} = 0\end{split}\]

Eq. (7.3-29) can be written as,

(7.3-30)\[a \times \alpha_{i + 1}^{k + 1} + G_{i + 1}^{k + 1} + c = 0\]

Writing the general energy Eq. (7.3-15) in terms of \(\alpha\) results in the following,

(7.3-31)\[\begin{split}\left[ \dot{\alpha}_{i + 1} \left(h \rho \right)_{fg} + \alpha_{i + 1} \left(h \dot{\rho} \right)_{fg} + \left( h \dot{\rho} \right)_{f} \right] \Delta Z - \left(\alpha_{i + 1} - \alpha_{i} \right) \left(h \rho \right)_{fg} \dot{Z}_{i} \\ = -\Delta \left(G h \right)_{i} + Q_{i} \Delta Z + \dot{P} \Delta Z\end{split}\]

The finite difference form of Eq. (7.3-31) is,

(7.3-32)\[\begin{split}\left[ \frac{1}{\Delta t} \left( \alpha_{i + 1}^{k + 1} - \alpha_{i + 1}^{k} \right) \left(h \rho \right)_{fg}^{k} + \alpha_{i + 1}^{k + 1} \left(h \dot{\rho} \right)_{fg}^{k} + \left(h \dot{\rho} \right)_{f}^{k} \right] \frac{1}{n} Z_{TP}^{k + 1} - \left(\alpha_{i + 1}^{k + 1} - \alpha_{i}^{k + 1} \right) \\ \left(h \rho \right)_{fg}^{k} \left[\frac{i - j}{n} \frac{1}{\Delta t} \left(Z_{TP}^{k + 1} - Z_{TP}^{k} \right) + \dot{Z}_{SC} \right] = -\bigg[ G_{i + 1}^{k + 1} \left(h_{f}^{k} + \frac{\alpha_{i + 1}^{k + 1} \rho_{g}^{k} h_{fg}^{k}}{\rho_{f}^{k} + \alpha_{i + 1}^{k + 1} \rho_{fg}^{k}} \right) + \\ G_{i}^{k + 1} \left(h_{f}^{k} + \frac{\alpha_{i}^{k + 1} \rho_{g}^{k} h_{fg}^{k}}{\rho_{f}^{k} + \alpha_{i}^{k + 1} \rho_{fg}^{k}} \right) \bigg] + Q_{i}^{k} \frac{1}{n} Z_{TP}^{k + 1} + \dot{P} \frac{1}{n} Z_{TP}^{k + 1}\end{split}\]

Rearranging Eq. (7.3-32) according to coefficients of \(\alpha_{i + 1}^{k + 1}\) and \(G_{i + 1}^{k + 1}\), the following results,

(7.3-33)\[\begin{split}\left\{ \frac{1}{\Delta t} \left(h \rho \right)_{fg}^{k} \frac{1}{n} Z_{TP}^{k + 1} + \left( h \dot{\rho} \right)_{fg}^{k} \frac{1}{n} Z_{TP}^{k + 1} - \left(h \rho \right)_{fg}^{k} \left[ \frac{i - j}{n} \frac{1}{\Delta t} \left(Z_{TP}^{k + 1} - Z_{TP}^{k} \right) + \dot{Z}_{SC} \right] \right\} \\ \times \alpha_{i + 1}^{k + 1} + G_{i + 1}^{k + 1} \left(h_{f}^{k} + \frac{\alpha_{i + 1}^{k + 1} \rho_{g}^{k} h_{fg}^{k}}{\rho_{f}^{k} + \alpha_{i + 1}^{k + 1} \rho_{fg}^{k}} \right) + \bigg\{ -\alpha_{i + 1}^{k} \frac{1}{\Delta t} \left(h \rho \right)_{fg}^{k} \frac{1}{n} Z_{TP}^{k + 1} \\ + \left(h \dot{\rho} \right)_{f}^{k} \frac{1}{n} Z_{TP}^{k + 1} + \alpha_{i}^{k + 1} \left(h \rho \right)_{fg}^{k} \left[ \frac{i - j}{n} \frac{1}{\Delta t} \left(Z_{TP}^{k + 1} - Z_{TP}^{k} \right) + \dot{Z}_{SC} \right] \\ -G_{i}^{k + 1} \left(h_{f}^{k} + \frac{\alpha_{i}^{k + 1} \rho_{f}^{k} h_{fg}^{k}}{\rho_{f}^{k} + \alpha_{i}^{k + 1} \rho_{fg}^{k}} \right) - Q_{i}^{k} \frac{1}{n} Z_{TP}^{k + 1} - \dot{P} \frac{1}{n} Z_{TP}^{k + 1} \bigg\} = 0\end{split}\]

If \(a'\) and \(c'\) represent the coefficient of \(a_{i + 1}^{k + 1}\) and the constant term respectively, Eq. (7.3-33) becomes,

(7.3-34)\[a' \alpha_{i + 1}^{k + 1} + G_{i + 1}^{k + 1} \left(h_{f}^{k} + \frac{\alpha_{i + 1}^{k + 1} \rho_{g}^{k} h_{fg}^{k}}{\rho_{f}^{k} + \alpha_{i + 1}^{k + 1} \rho_{fg}^{k}} \right) + c' = 0\]

When the mass Eq. (7.3-30) is substituted into Eq. (7.3-34), a quadratic in \(a_{i + 1}^{k + 1}\) results,

(7.3-35)\[\begin{split}\left(\alpha_{i + 1}^{k + 1} \right)^{2} \left[a' \rho_{fg}^{k} - a h_{f}^{k} \rho_{fg}^{k} - a \rho_{g}^{k} h_{fg}^{k} \right] + \alpha_{i + 1}^{k + 1} \left[a' \rho_{f}^{k} - c \rho_{fg}^{k} h_{f}^{k} \right. \\ - c \rho_{g}^{k} h_{fg}^{k} + c' \rho_{fg}^{k} - ah_{f}^{k} \rho_{f}^{k} + \left[ c' \rho_{f}^{k} - c h_{f}^{k} \rho_{f}^{k} \right] = 0\end{split}\]

Several points need to be noted here. An inspection of Eq. (7.3-28) and Eq. (7.3-32) shows that both \(\alpha_{i + 1}\) and \(G_{i + 1}\) are totally implicit in time. It cannot be emphasized enough how much this feature of the boiling zone numerical solution enhances the stability of the calculation compared to other numerical schemes which are semi‑implicit in time which were also tried. In order to preserve a linearized set of equations, it is necessary that the void fractions and mass flows be semi‑implicit in time and this has a strong tendency to produce instabilities. The only quantities which are explicit in time are the saturation properties which are functions of pressure alone and the volumetric heat source term. Saturation properties are very well behaved functions of time since pressure tends to be a relatively stable function of time in most transients and the saturation properties are not as sensitive to changes in pressure as other quantities are sensitive to changes over time.

The last point concerns the \(k + 1\) superscript on \(Z_{TP}\), the length of the two‑phase zone. What this indicates, as noted above, is that the current value of the zone length in the iterative process is used in Eq. (7.3-30) and Eq. (7.3-35). Eq. (7.3-25) is solved for \(\alpha_{i + 1}^{k + 1}\) and then \(G_{i + 1}^{k + 1}\) is obtained from the continuity Eq. (7.3-30) for each node. At first, the value of \(Z_{TP}\) from the last time step (i.e. \(Z_{TP}^{k}\)) is used to solve for \(\alpha_{i + 1}^{k + 1}\) and \(G_{i + 1}^{k + 1}\) over the whole mesh starting at the bottom \(\left(i = 1 \right)\) where \(a_{i}^{k + 1}\) and \(a_{i}^{k + 1} \left( = 0 \right)\) are the known boundary conditions. The solution then proceeds upwards until \(\alpha_{i + 1}^{k + 1}\) is calculated. \(\alpha_{i + 1}^{k + 1}\) compared to 1.0 and if it is greater than 1.0, \(Z_{TP}\) is reduced for the next iteration and if it is less than 1.0, \(Z_{TP}\) is increased. The search on \(Z_{TP}\) continues until \(\alpha_{i + 1}^{k + 1}\) is sufficiently close to 1.0. If the boiling zone extends to the top of the steam generator, the same procedure is used, but no iteration on \(Z_{TP}\) is necessary since \(Z_{TP}\) is a fixed, known value.

7.3.3.1.4. Superheated Vapor Region

A compressible treatment of the vapor is used above the boiling zone and simultaneous nodal mass and energy equations are solved for nodal enthalpies and mass flows since the region length is known, being the remainder of the steam generator length after computing new subcooled and boiling zone lengths. The nodal densities and enthalpies are treated partially explicitly in time. Boundary conditions are the saturated vapor enthalpy and the mass flow at the bottom of the zone. The solution proceeds upwards to the top of the steam generator.

Since there is an expression for \(\rho\) as a function of enthalpy and pressure,

(7.3-36)\[\dot{\rho} = \frac{\partial \rho}{\partial h} \frac{\partial h}{\partial t} + \frac{\partial \rho}{\partial P} \frac{\partial P}{\partial t}\]

By substituting Eq. (7.3-36) into the mass Eq. (7.3-8), an expression for \(G_{i + 1}\) as a function of \(h_{i + 1}\) results,

(7.3-37)\[G_{i + 1} = G_{i} - \left[ \frac{\partial \rho}{\partial h} \dot{h}_{i + 1} + \frac{\partial \rho}{\partial P} \dot{P} \right] \Delta Z + \Delta \rho_{i} \dot{Z}_{i}\]

Next, Eq. (7.3-36) is substituted into Eq. (7.3-15), the following results

(7.3-38)\[\begin{split}\left[ \frac{\partial \rho}{\partial h} \dot{h}_{i + 1} + \frac{\partial \rho}{\partial P} \dot{P} \right] h_{i + 1} \Delta Z + \rho_{i + 1} \dot{h}_{i + 1} \Delta Z - \Delta \left(\rho h \right)_{i} \dot{Z}_{i} \\ = - G_{i + 1} h_{i + 1} + G_{i} h_{i} + Q_{i} \Delta Z + \dot{P} \Delta Z\end{split}\]

Now, substituting the expression for \(G_{i + 1}\) which results from the continuity Eq. (7.3-37) into the energy Eq. (7.3-38) and simplifying,

(7.3-39)\[\rho_{i + 1} \dot{h}_{i + 1} \Delta Z + \rho_{i} h_{i} \dot{Z}_{i} = - G_{i} h_{i + 1} + \rho_{i} h_{i + 1} \dot{Z}_{i} + G_{i} h_{i} + Q_{i} \Delta Z + \dot{P} \Delta Z\]

The finite difference form of Eq. (7.3-39) is,

(7.3-40)\[\begin{split}\frac{1}{\Delta t} \left(h_{i + 1}^{k + 1} - h_{i + 1}^{k} \right) \rho_{i + 1}^{k} \frac{1}{n} Z_{SH}^{k + 1} + h_{i}^{k + 1} \rho_{i}^{k + 1} \frac{i - j}{n} \dot{Z}_{SH}^{k + 1} = -G_{i}^{k + 1} h_{i + 1}^{k + 1} + h_{i + 1}^{k + 1} \rho_{i}^{k + 1} \frac{i - j}{n} \dot{Z}_{SH}^{k + 1} \\ + G_{i+}^{k + 1} h_{i}^{k + 1} + Q_{i}^{k} \frac{1}{n} Z_{SH}^{k + 1} + \dot{P} \frac{1}{n} Z_{SH}^{k + 1}\end{split}\]

Eq. (7.3-40) is entirely implicit in enthalpy, mass flow and zone length. However, it is necessary to use the beginning‑of‑step value of \(\rho_{i + 1}\) since density is a complicated function of enthalpy and pressure and there is no way to incorporate this function in Eq. (7.3-20) and preserve linearity. \(\rho_{i}\), however, is entirely implicit since the solution proceeds upwards in the mesh and \(\rho_{i}\) can be updated as the solution proceeds along the mesh. By solving for \(h_{i + 1}^{k + 1}\), the following results,

(7.3-41)\[h_{i + 1}^{k + 1} = \frac{h_{i}^{k + 1} \left( G_{i}^{k + 1} - \rho_{i}^{k + 1} \frac{i - j}{n} \dot{Z}_{SH}^{k + 1} \right) + \frac{1}{n} Z_{SH}^{k + 1} \left(\frac{1}{\Delta t} h_{i + 1}^{k} \rho_{i + 1}^{k} + Q_{i}^{k} + \dot{P}^{k} \right)}{G_{i}^{k + 1} + \frac{1}{\Delta t} \rho_{i + 1}^{k} \frac{1}{n} Z_{SH}^{k + 1} - \rho_{i}^{k + 1} \frac{i - j}{n} \dot{Z}_{SH}^{k + 1}}\]

The finite‑difference form of Eq. (7.3-37) is,

(7.3-42)\[G_{i + 1}^{k + 1} = G_{i}^{k + 1} - \left[ \frac{\partial \rho}{\partial h} \frac{\left(h_{i + 1}^{k + 1} - h_{i + 1}^{k} \right)}{\Delta t} + \frac{\partial \rho}{\partial P} \dot{P} \right] \frac{1}{n} Z_{SH}^{k + 1} + \left(\rho_{i + 1}^{k + 1} - \rho_{i}^{k + 1} \right) \dot{Z}_{SH}\]

After obtaining \(h_{i+1}^{k+1}\) from Eq. (7.3-41), \(\rho_{i+1}^{k+1}\) is calculated as a function of \(h_{i+1}^{k+1}\) and \(P^{k+1}\) and these are used to calculate \(G_{i + 1}^{k + 1}\) in Eq. (7.3-42). It should be noted that the partial derivatives of density with respect to enthalpy and pressure are evaluated with the \(h_{i + 1}^{k + 1}\) and \(\rho_{i + 1}^{k + 1}\) just calculated. Starting at the bottom of the mesh, \(G_{1}^{k + 1}\) and \(h_{1}^{k + 1} \left( = h_{g} \right)\) are known and each parameter is solved for at the top of the cell at the \(i + 1\) location according to the above procedure up to the top of the steam generator.

7.3.3.1.5. Sodium Side Calculation

Incompressible flow is assumed on the sodium side because it is always in the liquid phase. Therefore there is no continuity equation. Also, since the sodium side is at relatively low pressure and has a stable pressure history, the pressure terms in the energy Eq. (7.3-13) are neglected. Next, since the sodium flows downward, in order to donor‑cell the energy equation, \(\left( \overline{\rho h} \right)_{i}\) is set equal to \(\left( \rho h \right)_{i}\). Lastly, it is convenient to assume that \(G\) is positive for downward-flowing sodium which means that \(- \Delta \left( G h \right)_{i}\) becomes \(-G \left[ h_{i} - h_{i + 1} \right]\). Thus Eq. (7.3-13) becomes,

(7.3-43)\[\left(\rho \dot{h} \right)_{i} \Delta Z - \left[\left( \rho h \right)_{i + 1} - \left( \rho h \right)_{i} \right] \dot{Z}_{i + 1} = -G \left(h_{i} - h_{i + 1} \right) + Q_{i} \Delta Z\]

Assuming \(\dot{\rho} = 0\) because of incompressible flow and rewriting Eq. (7.3-43) in terms of temperature (and neglecting the \(\dot{c}_{p}\) term as unimportant), the following results,

(7.3-44)\[\overline{\rho}_{i} \overline{c}_{p, i} \dot{T}_{i} \Delta Z - \overline{\rho}_{i} \overline{c}_{p, i} \left(T_{i + 1} - T_{i} \right) \dot{Z}_{i + 1} = -G \overline{c}_{p, i} \left(T_{i} - T_{i + 1} \right) + Q_{i} \Delta Z\]

The \(\overline{c}_{p, i}\) and the \(\overline{\rho}_{i}\) are computed using the sodium temperature at the cell‑center. (This is a slight inaccuracy but, given the fact that liquid sodium properties are so well‑behaved and change so gradually, it is of small consequence.) The finite difference form of Eq. (7.3-44) is,

(7.3-45)\[\frac{\overline{\rho}_{i}^{k}}{\Delta t} \left(T_{i}^{k + 1} - T_{i}^{k} \right) \Delta Z^{k + 1} - \overline{\rho}_{i}^{k} \left(T_{i + 1}^{k + 1} - T_{i}^{k} \right) \dot{Z}_{i + 1}^{k + 1} = -G^{k + 1} \left(T_{i}^{k + 1} - T_{i + 1}^{k + 1} \right) + \frac{\Delta Z^{k + 1}}{\overline{c}_{p, i}} Q_{i}^{k}\]

Note that the \(\overline{\rho}_{i}\) and the \(\overline{c}_{p, i}\) are computed with beginning-of-step temperatures and that the \(\Delta Z\) and \(\dot{Z}_{i + 1}\) are the end-of-step quantities just calculated in the water side calculation. \(Q_{i}\) is, of course, explicit in time as usual and the mass flow provided by the external sodium loop calculation is the new end-of-time-step value. If Eq. (7.3-45) is now solved for \(T_{i}^{k + 1}\), the following results,

(7.3-46)\[T_{i}^{k + 1} = \frac{T_{i + 1}^{k + 1} \left(G^{k + 1} + \overline{\rho}_{i}^{k} \dot{Z}_{i + 1}^{k + 1} \right) + T_{i}^{k} \frac{\Delta Z^{k + 1}}{\Delta t} \overline{\rho}_{i}^{k} + \frac{\Delta Z^{k + 1}}{\overline{c}_{p, i}} Q_{i}^{k}}{ \frac{\Delta Z^{k + 1}}{\Delta t} \overline{\rho}_{i}^{k} + \overline{\rho}_{i}^{k} \dot{Z}_{i + 1}^{k + 1} + G^{k + 1}}\]

Starting at the top of the steam generator, with the new inlet sodium temperatures at the end of the time step, the calculation proceeds downward to the bottom of the mesh.

7.3.3.1.6. Wall Temperature Calculation

The heat capacity of the tube wall must be taken into account during the transient. Since there is no convective term in the energy equation, central differencing is used. This means that \(\left( \overline{\rho h} \right)_{i} = \frac{1}{2} \left[ \left( \rho h \right)_{i + 1} + \left( \rho h \right)_{i} \right]\) in Eq. (7.3-13) which becomes,

(7.3-47)\[\frac{d}{dt} \left\{ \frac{1}{2} \left[\left(\rho h \right)_{i + 1} + \left( \rho h \right)_{i} \right] \Delta Z \right\} - \left(\rho h \right)_{i + 1} \dot{Z}_{i + 1} + \left( \rho h \right)_{i} \dot{Z}_{i} = Q_{i} \Delta Z\]

Eq. (7.3-47) is written in terms of temperature and both \(\rho\) and \(c_{p}\) are assumed to be temperature independent. This results in the following,

(7.3-48)\[\begin{split}\frac{d}{dt} \left\{ \frac{1}{2} \left(T_{i + 1} + T_{i} \right) \right\} \Delta Z + \frac{1}{2} \left( T_{i + 1} + T_{i} \right) \left( \dot{Z}_{i + 1} - \dot{Z}_{i} \right) - T_{i + 1} \dot{Z}_{i + 1} \\ + T_{i} \dot{Z}_{i} = \frac{\Delta Z}{\rho c_{p}} Q_{i}\end{split}\]

Since the wall temperature is tracked at the cell center, not the cell edge, the quantity desired is \(\overline{T_{i}} = \frac{1}{2}(T_{i + 1} + T_{i})\). Thus Eq. (7.3-48) becomes, after simplification,

(7.3-49)\[\dot{\overline{T}} = \frac{1}{\rho c_{p}} Q_{i}^{k} + \frac{1}{2} \frac{1}{\Delta Z^{k + 1}} \left(T_{i + 1}^{k} - T_{i}^{k} \right) \left( \dot{Z}_{i + 1}^{k + 1} + \dot{Z}_{i}^{k + 1} \right)\]

The heat source is explicit in time and the \(Delta Z\) and \(\dot{Z}\) terms are the end-of‑step values from the water side calculation. The difficulty with this equation is calculating the cell‑edge values \(T_{i + 1}\) and \(T_{i}\) since the wall temperatures are tracked at the cell center. Therefore interpolated or extrapolated estimates of the cell‑edge values are formed from the cell‑center temperatures.

7.3.3.1.7. Calculation of Boiling Crisis Point

The point of boiling crisis, or DNB point, in the boiling zone is computed by tracking the continuously varying intersection of two functions which is a point within the node structure. The first function represents the required heat flux for the boiling crisis to occur and the second is the actual local heat flux at the wall surface.

The DNB heat flux correlation [7-3] is as follows,

(7.3-50)\[F_{D} = 7.84 \times 10^{8} \left[ \chi h_{fg} \rho_{g} / \rho_{f} \sqrt{\frac{G}{1355}} \right]^{-0.667}\]

This correlation is evaluated at each cell center in the boiling zone using the local quality. The inlet mass flux \(G\) is used instead of the local mass flux to enhance numerical stability although the original correlation used the local flow.

An expression for the wall surface heat flux is obtained as follows. There is a correlation for the heat transfer coefficient at the tube wall surface but the wall surface temperature is unknown, although the mid‑wall temperature and the water temperature at saturation are known. Without going into the details of the correlation here (see Section 7.7.2), it is known that the heat flux at the wall surface, \(F_{S}\), is equal to \(a \left(T_{S} - T_{sat} \right)^{2}\), where \(T_{S}\) is the wall surface temperature and \(a\) is only a function of pressure. The heat flux between the mid‑wall and the wall surface, \(F_{M}\), is \(b \left( T_{M} - T_{S} \right)\), where \(b\) is the inverse of the wall heat resistance and \(T_{M}\) is the mid-wall temperature. When \(F_{S}\) is set equal to \(F_{M}\), a quadratic in \(\left(T_{S} - T_{sat} \right)\) results,

(7.3-51)\[a\left( T_{S} - T_{\text{sat}} \right)^{2} + b\left( T_{S} - T_{\text{sat}} \right) - b\left( T_{M} - T_{\text{sat}} \right) = 0\]

Thus the wall surface temperature is obtained and then the heat flux at the wall surface, \(F_{S}\), which is computed at each cell center over the length of the boiling zone. There are thus two functions, \(F_{S}\) and \(F_{D}\), with values at each cell. In order to obtain the intersection of these two functions and thus the point of boiling crisis, a linear approximation is made to each function proceeding two cells at a time along the length of the steam generator until an intersection of the two lines is reached. The intersection point is tracked exactly and the nucleate boiling and film boiling heat transfer coefficients are prorated in the cell where the intersection occurs. This method gives a smoothly varying, stable calculation of the DNB point.

7.3.3.1.8. Disappearing and Appearing Regions

When the length of a zone is reduced below a certain value, the number of nodes within the zone is reduced from whatever initial number there were in the zone to only one node. However, no matter how long the zone is, no more than the initial number of nodes will be used in the zone. Reducing the number of nodes for small zone lengths greatly enhances numerical stability while reducing computer time and, so long as the criterion for the node reduction is not too large, very little accuracy in the calculation is sacrificed. When the node structure is collapsed to one node, the cell‑edge quantities at the inlet and outlet to the zone remain unchanged while the intermediate values are eliminated. The tube wall temperature in the center of the new l‑node region is formed as an average of two wall temperatures nearest the center of the old multi‑node region. When the zone length increases beyond a certain value and there is only one node in the region then the number of nodes is reset at the original value and the values of parameters at intermediate nodes must be initialized. This is done with simple linear fits (close enough considering the short lengths involved) between the end point values for sodium temperatures, for enthalpies in the subcooled and superheated zones and for mass flows in the boiling and superheated regions. When the boiling zone has only one node and when it is reinitialized at the original number of nodes, the whole region is assumed to be in the nucleate boiling regime.

When a second length threshold is reached as a region’s length is reduced, then the region is eliminated entirely. This only applies to the boiling and superheated zones and they must disappear in order. That is if there is a superheated zone, there must be a boiling zone no matter how small. When the superheated zone disappears, then the boiling zone outlet enthalpy (i.e. void fraction or quality) becomes a free variable rather than fixed at \(h_{g}\) as it is when a superheated zone exists. The criterion for elimination of the superheated zone is a length criterion but the criterion for recreating the superheated zone is that the outlet enthalpy of the boiling zone be somewhat higher than \(h_{g}\). The mass flow at the outlet of the newly created superheated zone is assumed the same as the outlet flow from the boiling zone. The outlet enthalpy is set to the value of the criterion and the boiling zone outlet enthalpy is set to \(h_{g}\). The length of the new superheated zone is computed according to the following formula,

(7.3-52)\[Z_{SH} = Z_{TP} \frac{h_{out} - h_{g}}{h_{out} - h_{f}}\]

where \(Z_{SH}\) is the new superheated length, \(Z_{TP}\) is the old boiling zone length before being reduced by \(Z_{SH}\) and \(h_{out}\) is the enthalpy calculated at the outlet of the steam generator. Values for the sodium and tube wall temperatures are interpolated according to the new node and zone structure.

The criterion for elimination of the boiling zone is again a length criterion but the criterion for recreating the boiling zone is that the outlet enthalpy of the subcooled zone be somewhat higher than \(h_{f}\). The mass flow at the outlet of the newly created boiling zone is assumed the same as the outlet flow from the subcooled zone. The outlet enthalpy is set to the value of the criterion and the subcooled zone outlet enthalpy is set to \(h_{f}\). The length of the new boiling zone is calculated as follows,

(7.3-53)\[Z_{TP} = Z_{SC} \frac{h_{out} - h_{f}}{h_{out} - h_{in}}\]

where \(Z_{TP}\) is the new boiling length, \(Z_{SC}\) is the old subcooled zone length before being reduced by \(Z_{TP}\), \(h_{out}\) is the enthalpy calculated at the outlet of the steam generator, and \(h_{in}\) is the inlet enthalpy. Values for the sodium and tube wall temperatures are interpolated as for the superheated zone creation above according to the new node and zone structure.

7.3.3.1.9. Miscellaneous Numerical Issues

Nothing has been said so far about the calculation of the time derivative of pressure which appears in the energy Eq. (7.3-15). At each call to the steam generator routine, the balance‑of‑plant calculation provides the new steam generator pressure at the end of the time step. It would seem natural to form \(\dot{P}\) with the current \(\Delta t\) and \(P^{k}\) and \(P^{k + 1}\). This, however, can lead to significant numerical instabilities caused by large temporary spikes in \(P\) even when the time‑averaged value of \(\dot{P}\) is well-behaved and much more gradual than would be predicted by using the stepwise values of \(P\). Therefore, a moving average of \(\dot{P}\) is computed over the last 2 \(m\) timesteps so that,

(7.3-54)\[\dot{P} = \frac{ \sum_{i = m + 1}^{2 m} P_{i} \Delta t_{i} - \sum_{i = 1}^{m} P_{i} \Delta t_{i}}{ \frac{1}{2} \sum_{i = 1}^{2 m} \Delta t_{i}}\]

There is a time step selector currently in the code which chooses a new timestep size for the next step based on information from the current step. However, this selector is preliminary and merely chooses the new step according to fractional changes in a number of parameters over the step. That is, the new time step is computed as follows,

(7.3-55)\[\Delta t' = \text{Min} \left(X \left| \frac{\Delta t Y_{i}^{k + 1}}{Y_{i}^{k + 1} - Y_{i}^{k}} \right| \right)\]

where \(X\) is an input fractional change in the quantity \(Y_{i}, \Delta t\) is the current time step, \(\Delta t'\) is the new time step and Min indicates that the minimum over all the \(Y_{i}\) values is computed. The various quantities indicated by \(Y\) include the sodium side flow, the zone boundaries, the steam generator pressure, the nodal water mass flows, the void fractions in the boiling zone, the enthalpies in the subcooled and superheated zones, the sodium temperatures and the tube wall temperatures. There is also a minimum value criterion for the new step set by the steam generator. There is in effect a maximum value for the time step which is set for the primary loop calculation. However, there is rarely any need for the steam generator to have a larger time step than the primary loop calculation and, almost always, it is the hydrodynamics on the water side of the steam generator which determines the time step.

There are two artificial limitations that are superimposed on the boiling zone calculation that need to be pointed out. The first is that the void fraction solved for in each successive node as the solution proceeds up the zone must be larger than the previous value at the last node. The code simply requires that the new void fraction be at least 0.001 larger than the last. This may seem like a major limitation in the solution method but, in practice, it is rarely used. When it is used, it has very little consequence for the calculation. The only time this fix is used is when there is an extremely flat void fraction profile (which can be caused by a number of things, very low water flow, for example). In the absence of this fix, there is occasionally a tendency for numerical instabilities to form when there is an extremely flat void profile. The other artificial limitation is that the boiling zone length is not allowed to change more than 1% in a time step. This can have some significant implications for the course of a transient. Without this limitation, there can be a tendency for the boiling zone length to adjust too rapidly to changing conditions, which can cause significant numerical instabilities since a large change in \(Z_{TP}\) over a short time produces a large \(\dot{Z}_{TP}\) and a large perturbation in the equation set. Since the effect is largely artificial, this limitation within certain bounds is consistent with the physical conditions of the case. However, limiting the change in \(Z_{TP}\) means that the void fraction at the top of the zone may not be equal to 1.0 and, if it is too different, then basic assumptions of the model are, of course, being violated. It must be emphasized, however, that this limitation, is not used frequently and, when it is used, the outlet void fraction nearly always remains close to 1.0 while, over a number of time steps, the region length changes to accommodate the changing conditions but avoiding large temporary values of \(\dot{Z}_{TP}\) which could drive the calculation unstable.

7.3.3.1.10. Calculation of Pressure Drop for Momentum Equation

Although the balance‑of‑plant calculation does the actual computation which produces the inlet flow for the steam generator and the pressure boundary conditions at the inlet and outlet plena of the steam generator, the steam generator must provide the pressure drops to the balance-of-plant for this calculation. For the details of the momentum equation solution, it is necessary to refer to the balance‑of‑plant description (Section 7.2). All that will be done here is to describe the pressure drop calculation itself. For each of the four zones corresponding to each of the four heat transfer regimes \(i\), the following is the pressure drop \(\Delta P\) across the zone,

(7.3-56)\[\Delta P_{i} = - \overline{G}_{i}^{2} \left(\frac{1}{\rho_{t}} - \frac{1}{\rho_{b}} \right) - Z_{i} \bigg[ \overline{\rho}_{i} 9.8 + \dot{\overline{G}}_{i} + \overline{G}_{i}^{2} 0.31 FR_{i} \left( \frac{\overline{G}_{i} D_{H}}{\overline{\mu}_{i}} \right)^{-0.25} \frac{1}{2} \frac{1}{D_{H} \overline{\rho}_{i}} R_{i} \bigg]\]

where \(\overline{G}_{i}\) is an average of the mass flow both spatially over the zone length and temporally over the time step; \(\rho_{t}\) is the density at the top of the zone and \(\rho_{b}\) at the bottom; \(Z_{i}\) is the zone length; \(\overline{\rho}_{i}\) the average density over the zone; \(\dot{\overline{G}}_{i}\) is the average mass flow over the zone length at the end of the time step minus the average mass flow over the zone at the beginning of the time step divided by the time step; \(FR_{i}\) is a calibration factor computed in steady state to provide the proper steady state pressure drop; \(D_{H}\) is the water side hydraulic diameter; and \(\overline{\mu}_{i}\) is the average viscosity for the regime. Eq. (7.3-56) is used to compute \(\Delta P_{i}\) for the subcooled, the nucleate boiling, the film boiling and superheated zones. The factor \(R_{i}\) is 1.0 for the subcooled and the superheated zones. \(R_{i}\) is computed according to the following formula in the two boiling zones,

(7.3-57)\[R_{i} = 0.95819 - \left( 1167.2 R_{i}' - 505. \right) R_{i}'\]

(7.3-58)\[R_{i}' = \frac{\overline{\chi}_{i}}{\left( \frac{P}{1.724 \times 10^{6}} \right)^{2.448} + 16.217}\]

where \(P\) is the steam generator pressure and \(\overline{\chi}_{i}\) is the average quality over each boiling zone. This formula is the Thom correlation [7-2] with constants appropriate for the units used in the code.

Once the \(\Delta P_{i}\)s have been calculated, then the \(\Delta P_{i}\)s for the boiling zones and the superheated vapor zone are summed and divided by the sum of all four \(\Delta P_{i}\)s. This gives the current fraction of the total pressure drop across the steam generator that is above the subcooled zone. The balance‑of‑plant model uses its current pressures at the inlet and the outlet plena of the steam generator to provide the total pressure drop and estimates the pressure at the top of the subcooled zone with the fractional pressure drop referred to above. The pressure at the top of the subcooled zone provides the balance‑of‑plant momentum equation with a pressure boundary condition and it can merely include the subcooled liquid zone of the steam generator as the last in a series of incompressible liquid segments bounded by plena which stretches from the feed water inlet to the lower end of the compressible zones in the steam generator (i.e. the subcooled/boiling boundary). Thus the inlet flow (constant throughout the subcooled zone) is determined as part of the solution matrix in the total balance‑of‑plant momentum equation. Of course, the steam generator must provide the balance‑of‑plant model with information about the subcooled zone. It needs the average density, the length of the zone, the friction normalization factor \(FR_{1}\), the average viscosity and the hydraulic diameter. It is clear that, in the case when the subcooled zone extends to the top of the steam generator, the whole steam generator becomes merely one incompressible segment in the balance‑of‑plant matrix from the feedwater inlet to the turbines.

7.3.3.2. Recirculation‑Type Steam Generator

As noted before, the modeling of the evaporator in this node of the steam generator model is done with the same coding as is used for the once-through type steam generator. The difference is that, when it is used as an evaporator, the outlet enthalpy will be less than or equal to \(h_{g}\). Since this is within the envelope of cases for which the once‑through modeling was designed, this has already been described above. The modeling of the steam drum is described elsewhere in detail (See Section 7.4).

There remains only the discussion of the modeling of the superheater. As noted above, it is assumed that incompressible flow is adequate to describe the superheater. The mass flow through the superheater is determined by the balance‑of‑plant momentum equation. The lower enthalpy boundary condition is \(h_{g}\). There are no region boundaries to calculate since there is only single phase vapor flow in the superheater. Since \(\dot{\rho} = 0\) is assumed, the energy Eq. (7.3-15) becomes, for the constant superheater length,

(7.3-59)\[\rho_{i + 1} \dot{h}_{i + 1} \Delta Z = - G\left(h_{i + 1} - h_{i} \right) + Q_{i} \Delta Z + \dot{P} \Delta Z\]

The finite difference form of Eq. (7.3-59) is,

(7.3-60)\[\rho_{i + 1}^{k} \Delta Z \frac{h_{i + 1}^{k + 1} - h_{i + 1}^{k}}{\Delta t} = - G^{k + 1} \left( h_{i + 1}^{k + 1} - h_{i}^{k + 1} \right) + Q_{i}^{k} \Delta Z + \dot{P} \Delta Z\]

Eq. (7.3-60) is then solved for \(h_{i + 1}^{k + 1}\) resulting in,

(7.3-61)\[h_{i + 1}^{k + 1} = \frac{\rho_{i + 1}^{k} \frac{\Delta Z}{\Delta t} h_{i + 1}^{k} + G^{k + 1}h_{i}^{k + 1} + Q_{i}^{k} \Delta Z + \dot{P} \Delta Z}{\rho_{i + 1}^{k} \frac{\Delta Z}{\Delta t} + G^{k + 1}}\]

Eq. (7.3-61) is solved for each successive \(h_{i + 1}^{k + 1}\) up to the top of the superheater. \(\Delta Z\) is, of course, a constant. The lower boundary conditions are \(h_{g}\) and \(\rho_{g}\). \(G^{k + 1}\) is provided by the balance‑of‑plant momentum equation.

The sodium side temperatures are solved according to the same method as used in the once‑through steam generator. All the same assumptions concerning incompressible flow and donor‑cell differencing are made. The only difference is that the \(\dot{Z}\) terms are eliminated and \(\Delta Z\) becomes a constant because of the constant superheater length. Thus Eq. (7.3-46) becomes,

(7.3-62)\[T_{i}^{k + 1} = \frac{T_{i + 1}^{k + 1} G^{k + 1} + T_{i}^{k} \frac{\Delta Z}{\Delta t} \overline{\rho}_{i}^{k} + \frac{\Delta Z}{\overline{c}_{p,i}} Q_{i}^{k}}{\frac{\Delta Z}{\Delta t} \overline{\rho}_{i}^{k} + G^{k + 1}}\]

As before, starting at the top of the steam generator, with the new inlet sodium temperature at the end of the time step, the calculation proceeds downward to the bottom of the mesh.

The same considerations apply to the tube wall temperature calculation in the superheater. The solution method is precisely the same as for the once-through steam generator except that the \(\dot{Z}\) terms are now eliminated because of the constant superheater length. Thus Eq. (7.3-49) becomes simply,

(7.3-63)\[\dot{\overline{T}}_{i} = \frac{1}{\rho c_{p}} Q_{i}^{k}\]

Thus there is no difficulty in calculating the \(\Delta T\) term as there was in Eq. (7.3-49) because it is eliminated.

7.3.3.3. Steady State Solution

7.3.3.3.1. Once‑Through Type Steam Generator

7.3.3.3.1.1. Superheated Vapor Region

For a given reactor power, the product of flow rate and enthalpy change across the steam generator must be the same on both the water and sodium sides. In other words, the following holds,

(7.3-64)\[RP = G_{w} A_{w} \left(h_{w, out} - h_{w, in} \right) = G_{s} A_{w} \overline{c}_{p,s} \left(T_{s, in} - T_{s, out} \right)\]

where \(RP\) is the reactor power (or a fraction thereof for multiple steam generators); \(G_{w}\) and \(G_{s}\) are the water and sodium flow rates; \(A_{w}\) and \(A_{s}\) are the water and sodium flow areas; \(h_{w, out}\) and \(h_{w, in}\) are the outlet steam and inlet water enthalpies; \(T_{s, in}\) and \(T_{s, out}\) are the inlet and outlet sodium temperatures; and \(\overline{c}_{p, s}\) is the average specific heat for sodium over the length of the steam generator. This relationship must determine the above flow rates, water enthalpies, geometry and sodium temperatures. Constraints on any of these parameters must translate into constraints on the other parameters according to the above relationship. For the present purpose, however, geometry, flow rates and inlet and outlet enthalpies are assumed to have been determined elsewhere.

For the steady state, then, \(h_{w, out}\) is presumed. If \(h_{w, out} > h_{g}\), then there is a superheated vapor zone. (Of course, in any true steady‑state operation for a once‑through steam generator, there will be a superheated vapor zone. However, this “steady‑state” calculation described here produces starting conditions for a transient calculation of any nature which may be very different than the normal operational conditions.) For the superheated vapor zone, then, the following relation holds,

(7.3-65)\[G_{w}A_{w} \left(h_{w, out} - h_{g} \right) = G_{s} A_{s} \overline{c}_{p, s} \left( T_{s, in} - T_{s, hg} \right)\]

where \(T_{s,hg}\) is the sodium temperature at the point of saturated vapor enthalpy on the water side and \(\overline{c}_{p, s}\) is the average value of the specific heat over the superheated vapor zone. If \(\overline{c}_{p, s}\) is known, then Eq. (7.3-65) can be used to determine \(T_{s,hg}\). As a practical matter, \(c_{p,s}\) varies only 2-3% and quite smoothly over the length of the steam generator. If Eq. (7.3-65) is solved for \(T_{s,hg}\) using \(c_{p,s}\) calculated with \(T_{s, in}\), then the average of \(T_{s, in}\) and \(T_{s, hg}\) are used to calculate \(c_{p, s}\) and if this process is repeated several times, then there is a negligible error in \(\overline{c}_{p, s}\) and thus in \(T_{s, hg}\).

In order to fully characterize the superheated zone, either the length of the zone must be specified or some calibrating factor on the water side heat transfer coefficient must be specified. This will become clear as the solution description continues. It is also possible to calibrate the sodium side heat transfer coefficient but it is assumed that the water side coefficient involves much more uncertainty. First, the form of the water side heat transfer coefficient is as follows,

(7.3-66)\[H_{T} = \frac{1}{\frac{1}{H_{w} CF} + WR + FL}\]

where \(H_{T}\) is the total water coefficient; \(H_{w}\) is the heat transfer coefficient between the tube wall surface and the bulk fluid; \(CF\) is some calibration factor to be determined; \(WR\) is the heat resistance of the tube wall; and \(FL\) is some additional resistance to take into account fouling at the wall surface. \(H_{w}\) is calculated for each heat transfer regime according to correlations given in the Section 7.5. The \(H_{w}\)s represent values for experimental conditions and therefore may need to be calibrated for full scale cases. \(WR\) is calculated from the tube wall geometry and properties. \(FL\) is specified by the code user in the input.

Before a full nodewise solution is obtained, a rough guess to initialize the iterative process of the final solution is required. The case of specifying the zone length \(Z_{SH}\) and computing the calibration factor is considered first. The following equates the average heat transfer in the zone from the bulk sodium to the tube wall with the portion of reactor power known to be derived from the superheated zone,

(7.3-67)\[G_{s} \frac{1}{Z_{SH}} \overline{c}_{p, s} \left(T_{s, in} - T_{s, hg} \right) = H_{s} \left( \overline{T}_{s} - \overline{T}_{m} \right) \frac{2 \pi r_{s} Z_{SH}}{A_{s} Z_{SH}}\]

\(T_{s, hg}\) is obtained from Eq. (7.3-64). \(\overline{T}_{s} = \frac{1}{2} \left(T_{s, in} + T_{s, hg} \right)\). \(r_{s}\) is the outer tube wall radius. \(\overline{T}_{m}\) averaged over the height of the zone. \(H_{s}\) is the total heat transfer on the sodium side including the wall resistance,

(7.3-68)\[H_{s} = \frac{1}{\frac{1}{H_{Na}} + WRNA}\]

where \(H_{Na}\) is the heat transfer coefficient from the tube surface to the bulk sodium and WRNA is the wall resistance on the sodium side of the tube. The correlation for \(H_{Na}\) is given in Section 7.7.2. \(H_{Na}\) is a function of \(G_{s}\), geometry and temperature. The temperature used is \(\overline{T}_{s}\). Eq. (7.3-67) is solved for \(\overline{T}_{m}\) which is inserted into the equation analogous to Eq. (7.3-67) on the water side,

(7.3-69)\[G_{s} \frac{1}{Z_{SH}} \left(h_{w, out} - h_{g} \right) = \frac{1}{\frac{1}{H_{w}CF} + WR + FL} \left(\overline{T}_{m} - \overline{T}_{w} \right) \frac{2 \pi r_{w} Z_{SH}}{A_{w} Z_{SH}}\]

where \(\overline{T}_{W}\) is the temperature derived from \(\overline{H}_{w} = \frac{1}{2} \left(h_{w, out} + h_{g} \right)\), \(r_{w}\) is the inner tube wall radius and \(H_{w}\) is calculated with properties derived from \(\overline{h}_{w}\). Thus Eq. (7.3-69) can be solved for \(CF\), the initial guess for the calibration factor on the superheated zone heat transfer coefficient when the zone length is specified. Alternatively, if the calibration factor \(CF\) is specified, and the zone length is unknown, then Eq. (7.3-67) and Eq. (7.3-69) form a set with two unknowns, \(\overline{T}_{m}\) and \(Z_{SH}\), which can be solved for easily. If there is only one node in the superheated zone, then the steady state solution is finished at this point.

In order to solve the nodal equations, a similar method is used for each node as in the 1-node approximation above. First, there is the nodal energy balance for cell \(i\) from node \(i\) to node \(i + 1\) (the solution proceeds from the bottom to the top of the mesh),

(7.3-70)\[G_{w}A_{w}\left( h_{w,i + 1} - h_{w,i} \right) = G_{s}A_{s}\ {\overline{c}}_{p,s,i}(T_{s,i + 1} - T_{s,i})\]

where \(\overline{c}_{p, s, i}\) is the specific heat corresponding to \(\frac{1}{2} \left(T_{s, i + 1} + T_{s, i} \right) = \overline{T}_{s, i}\) This equation can be solved for \(T_{s, i + 1}\) which results in

(7.3-71)\[T_{s, i + 1} = \left[ \frac{G_{w} A_{w}}{G_{s} A_{s} \overline{c}_{p, s, i}} \right] h_{w, i + 1} + \left[T_{s, i} - \frac{G_{w} A_{w}}{G_{s} A_{s} \overline{c}_{p, s, i}} h_{w, i} \right]\]

which can be written as,

(7.3-72)\[T_{s, i + 1} = a h_{w, i + 1} + b\]

Next, the sodium side heat transfer is described by the following,

(7.3-73)\[G_{s} \frac{1}{\Delta z} \overline{c}_{p, s, i} \left(T_{s, i + 1} - T_{s, i} \right) = H_{s, i} \left[\frac{1}{2} \left(T_{s, i + 1} + T_{s, i} \right) - T_{m, i} \right] \frac{2 \pi r_{s} \Delta Z}{A_{s} \Delta Z}\]

where \(H_{s, i}\) is calculated according to Eq. (7.3-68) with \(\overline{T}_{s, i}\) and \(T_{m, i}\) is the cell-center value and \(\Delta Z\) is of course \(\frac{1}{n} Z_{SH}\) with \(n\) the number of cells in the zone. Eq. (7.3-73) is solved, for \(T_{m, i}\) in the following,

(7.3-74)\[T_{m, i} = \left[ \frac{1}{2} - \frac{G_{s} \overline{c}_{p, s, i} A_{s}}{H_{s, i} 2 \pi r_{s} \Delta Z} \right] T_{s, i + 1} + \left[ \frac{1}{2} + \frac{G_{s} \overline{c}_{p, s, i} A_{s}}{H_{s, i} 2 \pi r_{s} \Delta Z} \right] T_{s, i}\]

which can be written as,

(7.3-75)\[T_{m, i} = c T_{s, i + 1} + d\]

and if Eq. (7.3-72) is substituted into Eq. (7.3-75),

(7.3-76)\[T_{m, i} = a c h_{w, i + 1} + \left(bc + d \right) = eh_{w, i + 1} + f\]

Similarly, the water side heat transfer is described by the following,

(7.3-77)\[G_{w} = \frac{1}{\Delta Z} \left(h_{w, i + 1} - h_{w, i} \right) = H_{T, i} \left(T_{m, i} - \overline{T}_{w, i} \right) \frac{2 \pi r_{w} \Delta Z}{A_{w} \Delta Z}\]

where \(H_{T, i}\) is calculated according to Eq. (7.3-66). Next \(\overline{T}_{w, i}\) is replaced by \(\frac{1}{2} \left[T_{w, i+1} + T_{w, i} \right]\) Then, use is made of the relation,

(7.3-78)\[h_{w, i + 1} - h_{w, i} = \overline{c}_{p, w, i} \left(T_{w, i + 1} - T_{w, i} \right)\]

Eq. (7.3-78) is solved for \(T_{w, i + 1}\) and then,

(7.3-79)\[\overline{T}_{w, i} = T_{w, i} + \frac{1}{2 \overline{c}_{p, w, i}} \left(h_{w, i + 1} - h_{w, i} \right)\]

Eq. (7.3-79) and Eq. (7.3-76) are substituted into Eq. (7.3-77), which results in the following,

(7.3-80)\[h_{w, i + 1} = \frac{G_{w} h_{w, i} - H_{T, i} \frac{2 \pi r_{w} \Delta Z}{A_{w}} \left[f - T_{w, i} + \frac{h_{w, i}}{2 \overline{c}_{p, w, i}} \right]}{G_{w} + \frac{H_{T, i} 2 \pi r_{w} \Delta Z}{A_{w}} \left[\frac{1}{2 \overline{c}_{p, w, i}} - e \right]}\]

When \(h_{w, i + 1}\) is computed, \(T_{m, i}\) and \(T_{s, i + 1}\) can also be found from Eq. (7.3-76) and Eq. (7.3-72).

Now that the basic method of solution of the nodal equation has been described, several points need to be emphasized. First, in the three equation set, Eq. (7.3-70), Eq. (7.3-73), and Eq. (7.3-77), there are the three unknowns \(T_{s, i + 1}\), \(T_{m, i}\) and \(h_{w, i + 1}\) which are solved for. However, Eq. (7.3-70) and Eq. (7.3-73) presume that \(\overline{c}_{p, s, i}\) is known. Eq. (7.3-73) presumes that \(H_{s, i}\) is known and this means that an average sodium temperature for the cell must be known. Eq. (7.3-77) presumes that \(H_{T, i}\) and \(\overline{c}_{p, w, i}\) are known and various physical properties are required to compute \(H_{T, i}\). All of these quantities are functions of \(\overline{T}_{s, i}\) and \(\overline{T}_{w, i}\) (or \(\overline{h}_{w, i}\)) which require \(T_{s, i + 1}\) and \(T_{w, i + 1}\) (or \(h_{w, i + 1}\)). Therefore, there is an iterative process required to produce better and better values for the various parameters after starting the whole process with some initial estimate of the \(T_{s, i}\)s and the \(h_{w, i}\)s. On the very first pass, the nodal values of \(T_{s, i}\) and \(h_{w, i}\) are simply linear interpolations between the end values but, since there are a number of iterations before the final result is obtained, the effect of this initial assumption is negligible.

Secondly, the main goal of the iterative procedure is to produce either a calibration factor for a specified length or a zone length for a specified calibration factor. The length or calibration factor is simply assumed in the above solution of the nodal equations and when the solution of all the nodal values is complete, then a new length or calibration factor is chosen if the result is not yet acceptable. The nodal solution begins at the point of saturated vapor enthalpy where the \(h_{w, i}\) is simply \(h_{g}\) and the \(T_{s, i}\) is \(T_{s, hg}\), produced from Eq. (7.3-65). It should be mentioned here that Eq. (7.3-65) produces a better and better value of \(T_{s, hg}\) on each iteration since the value of \(\overline{c}_{p, s}\) used is refined by a recomputation after each iteration by using the new nodal \(T_{s, i}\)s calculated in the iteration. The nodal solution proceeds upwards from \(h_{g}\) and \(T_{s, hg}\) to the top of the steam generator where values of \(h_{w, out}\) the \(T_{s, in}\) are calculated. At this point, the criterion for convergence needs to be determined. The new values of \(h_{w, out}\) and \(T_{s, in}\) can both be compared to the externally calculated values. It was decided to use \(T_{s, in}\) as the criterion and thus the length or calibration factor is adjusted until the \(T_{s, i + 1}\) at the top of the steam generator is as close to \(T_{s, in}\) as necessary according to an input criterion. There is only one last point to note. This is that for each outer iteration which uses a new length or calibration factor, there are ten inner iterations for each node in the nodal solution which are necessary to converge on values of the heat transfer coefficients and \(c_{p}\)s for an assumed length or calibration factor. If this inner iteration is not done, the outer iteration will not converge.

7.3.3.3.1.2. Subcooled Liquid Region

Because of the difficulty of obtaining a solution for the boiling zone unless the length of the boiling zone is known, the subcooled zone solution, which may not have its length specified, is completed before the boiling zone. Once the lengths for both the superheated vapor zone and the subcooled liquid zone are determined, the length of the boiling zone is, of course, merely the remainder of the steam generator length. There is a boiling zone, however, only when \(h_{w, out} > h_{f}\).

(7.3-81)\[G_{w}A_{w}\left( h_{w,t} - h_{f} \right) = G_{s}A_{s}{\overline{c}}_{p,s}(T_{s,t} - T_{s,hf})\]

where \(h_{w, t}\) is \(h_{g}\) when there is a superheated vapor zone and \(h_{w, out}\) when there is not; \(T_{s, t}\) is \(T_{s, hg}\) when there is a superheated vapor zone and \(T_{s, in}\) when there is not; \(\overline{c}_{p, s}\) is the average value of the specific heat over the boiling zone. As is similar to Eq. (7.3-65), \(\overline{c}_{p, s}\) is first calculated with \(T_{s, t}\) and then with an average of \(T_{s, t}\) and \(T_{s, hf}\) and this process is repeated several times thus producing better and better values of \(T_{s, hf}\).

As was the case with the superheated zone, either the length of the subcooled zone or the calibration factor on its heat transfer coefficient must be specified. The total water side heat transfer coefficient is calculated as in Eq. (7.3-66) with a different correlation for \(H_{w}\) and perhaps a different value for \(FL\).

Again, as with the superheated zone, a one-node initial guess for the subcooled zone length \(Z_{SC}\) or calibration factor is obtained starting with an equation analogous to Eq. (7.3-67),

(7.3-82)\[G_{s} \frac{1}{Z_{SC}} \overline{c}_{p, s} \left(T_{s, u} - T_{s, out} \right) = H_{s} \left( \overline{T}_{s} - \overline{T}_{m} \right) \frac{2 \pi r_{s} Z_{SC}}{A_{s} Z_{SC}}\]

where \(T_{s, u}\) is either \(T_{s, in}\) when there is no boiling zone or \(T_{s, hf}\) which is obtained from Eq. (7.3-81), \(\overline{T}_s = \frac{1}{2}\left(T_{s,u} - T_{s,out} \right)\), \(\overline{T}_{m}\) is the midwall tube temperature averaged over the height of the zone and \(H_{s}\) is defined in Eq. (7.3-68). Again \(\overline{T}_{m}\) is obtained from Eq. (7.3-82) and inserted into the analogous equation to Eq. (7.3-69),

(7.3-83)\[G_{s} \frac{1}{Z_{SC}} \left(h_{w, u} - h_{w, in} \right) = \frac{1}{\frac{1}{H_{w} CF} + WR + FL } \left( \overline{T}_{m} - \overline{T}_{w} \right) \frac{2 \pi r_{w} Z_{SC}}{A_{w} Z_{SC}}\]

where \(h_{w, u}\) is \(h_{w, out}\) when there is no boiling zone and \(h_{f}\) when there is a boiling zone and \(\overline{T}_{w}\) is the temperature derived from \(\frac{1}{2} \left(h_{w, u} + h_{w, in} \right)\). Eq. (7.3-83) is solved for the initial guess for \(CF\) when the zone length is specified. Alternatively, if the calibration factor \(CF\) is specified, then the Eq. (7.3-82) and Eq. (7.3-83) form a set with two unknowns, \(\overline{T}_{m}\) and \(Z_{SC}\) which are then solved for. If there is only one node in the subcooled zone, the steady state solution is finished here.

In order to solve the nodal equations, the same method is used as was used for the superheated vapor zone except the nodewise solution proceeds from the top of the subcooled zone to the bottom of the steam generator. The nodal energy balance for a cell is exactly the same as Eq. (7.3-70). However, since the direction of solution is from top to bottom, \(T_{s, i}\) is solved for,

(7.3-84)\[T_{s, i} = \left[ \frac{G_{w} A_{w}}{G_{s} A_{s} \overline{c}_{p, s, i}} \right] h_{w, i} + \left[ T_{s, i + 1} - \frac{G_{w} A_{w}}{G_{s} A_{s} \overline{c}_{p, s, i}} h_{w, i + 1} \right]\]

which is written as,

(7.3-85)\[T_{s, i} = a h_{w, i} + b\]

As before, the sodium side heat transfer is described by Eq. (7.3-73). As before, Eq. (7.3-73) is solved for \(T_{m, i}\) which results in Eq. (7.3-34). However, since \(T_{s, i}\) is the unknown now and not \(T_{s, i + 1}\), Eq. (7.3-74) is written as,

(7.3-86)\[T_{m, i} = c t_{s, i} + d\]

and Eq. (7.3-85) is substituted into Eq. (7.3-86),

(7.3-87)\[T_{m, i} = ac h_{w, i} + \left( bc + d \right) = e h_{w, i} + f\]

The water side heat transfer is described by Eq. (7.3-77) just as for the superheated vapor zone, but Eq. (7.3-78) is solved for \(T_{w, i}\) and,

(7.3-88)\[\overline{T}_{w, i} = T_{w, i + 1} - \frac{1}{2 \overline{c}_{p, w, i}} \left(h_{w, i + 1} - h_{w, i} \right)\]

Eq. (7.3-88) and Eq. (7.3-87) are substituted into Eq. (7.3-77) which results in the following,

(7.3-89)\[h_{w, i} = \frac{G_{w} h_{w, i + 1} - H_{T, i} \frac{2 \pi r_{w} \Delta Z}{A_{w}} \left[f - T_{w, i + 1} + \frac{h_{w, i + 1}}{2 \overline{c}_{p, w, i}} \right]}{G_{w} + \frac{H_{T, i} 2 \pi r_{w} \Delta Z}{A_{w}} \left[e - \frac{1}{2 \overline{c}_{p, w, i}} \right]}\]

As before, when \(h_{w, i}\) is computed, \(T_{m, i}\) and \(T_{s, i}\) can also be found from Eq. (7.3-87) and Eq. (7.3-85). The same general considerations apply to the solution of the subcooled zone equation set as applied to the superheated vapor zone equation set. The criterion for convergence is now that \(T_{s, i}\) at the bottom of the mesh be arbitrarily close to \(T_{s, out}\). The subcooled zone length or the calibration factor \(CF\) is adjusted until this is achieved.

7.3.3.3.1.3. Boiling Zone

If \(h_{w, out} > h_{f}\), then there is a boiling zone. It has already been shown how the sodium temperatures were determined at each end of the zone, \(T_{s, in}\) or \(T_{s, hg}\) (depending on whether or not there is a superheated zone) and \(T_{s, hf}\). The water enthalpies at the ends of the zone are either \(h_{w, out}\) or \(h_{g}\) and \(h_{f}\). Since the lengths of the superheated vapor and subcooled liquid zones have been determined either by input specification or by the steady state calculation before the boiling zone calculation begins, the length of the boiling zone is also determined and it remains, therefore, to adjust the heat transfer in the boiling zone so that with the known zone length the enthalpy condition at the top of the zone is obtained. That is, either \(T_{s, in}\) or \(T_{s, hg}\) is obtained on the sodium side and \(h_{w, out}\) or \(h_{g}\) on the water side, although the actual criterion used, as in the other zones, is the sodium temperature. There is a complicating factor when trying to adjust the heat transfer in the boiling zone which does not exist in the other two zones, however. This is the fact that there are two heat transfer regimes in the boiling zone separated at the DNB point. Both the calibrating factors on both the heat transfer coefficients cannot be adjusted independently or the solution won’t converge. Therefore, the calibrating factor is fixed arbitrarily at a constant value in the nucleate boiling zone while the calibrating factor in the film boiling zone is adjusted to obtain the proper outlet conditions. A related problem is to determine where the DNB point is in the zone. This is done by using the method outlined in the transient section as the solution proceeds up the mesh and when the intersection of the two functions is determined by extrapolation of the two functions, the DNB point is predicted there.

The method of solution, then, is to proceed upwards in the mesh node‑by-node in the nucleate boiling zone using the known zone length and the assumed heat transfer coefficient calibration factor and extrapolating ahead to determine the DNB point. When the DNB point is found in a particular cell, then the calculation for that cell is repeated in order to use the properly prorated heat transfer coefficient (apportioned between the nucleate and the film boiling coefficients) for that cell. Then the solution switches to the film boiling zone and then proceeds to the top of the boiling zone and compares the sodium temperature obtained at the top to either \(T_{s, hg}\) or \(T_{s, in}\). Before the calculation proceeds node‑by‑node through the film boiling zone on the first iteration, however, an initial guess is made of the calibration factor in the zone is made on a one‑node basis just as was done with Eq. (7.3-67) and Eq. (7.3-69) in the superheated vapor zone. The only difference is that the sodium and water \(\Delta T\) and \(\Delta h\) are now appropriate for the boiling zone and \(\overline{T}_{w}\) becomes \(T_{sat}\). The calibration factor applied to the film boiling heat transfer coefficient is adjusted on each iteration until the sodium temperature at the top of the zone satisfies the criterion. If, as the calculation proceeds upwards in the mesh, no DNB point is predicted before the top of the boiling zone is reached, then it is assumed there is no film boiling zone and the calibration factor in the nucleate boiling zone, otherwise constant, is searched upon until the criterion at the top of the zone is satisfied.

In order to solve the nodal equations, a method similar to that used in the superheated vapor zone is used. First a nodal energy balance equation exactly the same as Eq. (7.3-70) is solved for \(T_{s, i + 1}\) as in Eq. (7.3-71) and rewritten as in Eq. (7.3-72). Again, \(T_{m, i}\) is solved for from the sodium side heat transfer Eq. (7.3-73) resulting in Eq. (7.3-74), rewritten as Eq. (7.3-75) and then Eq. (7.3-76). The water side heat transfer equation is slightly simpler than in the superheated zone because the water temperature is known at each node to be \(T_{sat}\). Eq. (7.3-77) becomes,

(7.3-90)\[G_{w} = \frac{1}{\Delta Z} \left(h_{w, i + 1} - h_{w, i} \right) = H_{T, i} \left( T_{m, i} - T_{sat} \right) \frac{2 \pi r_{w} \Delta Z}{A_{w} \Delta Z}\]

Eq. (7.3-90) is solved for \(h_{w, i + 1}\) after \(T_{m, i}\) is replaced with \(e h_{w, i + 1} + f\) from Eq. (7.3-76). The result is the following,

(7.3-91)\[h_{w,i + 1} = \frac{G_{w} h_{w, i} + H_{T, i} \frac{2 \pi r_{w} \Delta Z}{A_{w}} \left(f - T_{sat} \right)}{G_{w} - h_{w, i} \frac{2 \pi r_{w} \Delta Z}{A_{w}} e}\]

As before, when \(h_{w, i + 1}\) is computed, \(T_{m, i}\) is found from Eq. (7.3-76) and \(T_{s, i + 1}\) from Eq. (7.3-72). The same considerations concerning the calculation of properties and heat transfer coefficients during the iterative process and concerning the inner and outer iterations apply to the boiling zone as apply to the superheated zone.

7.3.3.3.1.4. Friction Factors for Momentum Equation

As mentioned before in the section concerning the calculation of the pressure drops in the steam generator, the factor \(FR_{i}\) for each heat transfer regime in Eq. (7.3-56) needs to be defined for steady state conditions. If the “steady state” calculation does not include all heat transfer regimes, then the \(FR_{i}\) for the missing zones is arbitrarily set to 1.0. First an unnormalized pressure drop \(\Delta P_{i}^{u}\) is calculated for heat transfer regime \(i\),

(7.3-92)\[\Delta P_{i}^{u} = -G_{w}^{2} \left( \frac{1}{\rho_{t}} - \frac{1}{\rho_{b}} \right) - Z_{i} \left[ \overline{\rho}_{i} 9.8 + G_{w}^{2} 0.31 \left( \frac{G_{w} D_{h}}{ \overline{\mu}_{i}} \right)^{-0.25} \frac{1}{2} \frac{1}{D_{\mu} \overline{\rho}_{i}} R_{i} \right]\]

where all parameters except \(G_{w}\) are defined as in Eq. (7.3-56). Next, a normalized pressure drop \(\Delta P_{i}^{n}\) is calculated,

(7.3-93)\[\Delta P_{i}^{n} = \Delta P_{i}^{u} \frac{\Delta P_{SG}}{\sum_{i} \Delta P_{i}^{u}}\]

where \(\Delta P_{SG}\) is the specified pressure drop across the entire steam generator length. The \(FR_{i}\)s are calculated as follows,

(7.3-94)\[FR_{i} = \frac{\frac{\Delta P_{i}^{n}}{Z_{i}} + 9.8 \overline{\rho}_{i} + \frac{G_{w}^{2}}{Z_{i}} \left(\frac{1}{\rho_{t}} - \frac{1}{\rho_{b}} \right) 2 D_{H} \overline{\rho}_{i}}{0.31 G_{w}^{2} \left( \frac{G_{w} D_{H}}{\overline{\mu}_{i}} \right)^{-0.25} R_{i}}\]

7.3.3.3.2. Recirculation‑Type Steam Generator

Only the superheater steady‑state condition needs to be described here since, as was explained above, the evaporator steady‑state is described in the once‑through steam generator section which can account for the situation with \(h_{w, out} \leq h_{g}\). The steady state solution for the superheater is identical with the steady‑state solution for the superheated vapor zone covered in the once‑through steam generator section. Obviously the option of the fixed length with the search on the calibration factor is the relevant option for the superheater. The water side outlet enthalpy is specified and the inlet water enthalpy is \(h_{g}\). The sodium inlet temperature, as before, is externally determined and the sodium temperature at the outlet of the superheater must be determined just as it is in Eq. (7.3-65). The solution proceeds upwards to the top of the superheater and the sodium temperature calculated at the top is compared to \(T_{s, in}\) and the calibration factor is adjusted until they are sufficiently close.