5.4.8. Stratified Volume Model

In addition to the uniform mixing compressible volume model described in Section 5.4.4, PRIMAR‑4 contains a stratified temperature model for the liquid in a compressible volume. This stratified model can be used for an outlet plenum and/or for a pool. This model borrows from the PLENUM‑2A model [5‑7] of Howard and Lorenz, but the PRIMAR‑4 model has been extended beyond the capabilities of the PLENUM‑2A model. Borrowed from PLENUM‑2A is the concept of a small number of distinct temperature regions in the coolant, separated by horizontal interfaces. Also, borrowed are the concept of distinct stages in the calculation, a plume height correlation, and a correlation for interface rise due to entrainment of a hot layer into a cooler plume rising from the core outlet. One extension of the PRIMAR‑4 model is the provision for handling up transients as well as down transients: PLENUM‑2A will only handle transients in which the core outlet temperature is cooler than the plenum temperature, whereas the PRIMAR‑4 model will also handle transients in which the core outlet temperature is hotter than the plenum temperature. Another extension is the option to handle a horizontal discharge from an IHX into a cold pool: PLENUM‑2A will only handle a vertical discharge from the core into an outlet plenum. The code handles up to three regions and five stages, whereas PLENUM‑2A considers only two regions and three stages. Also, the PRIMAR‑4 model treats thermal conduction across the interface between regions, and this model includes detailed multi‑node wall temperature calculations.

Figure 5.4.9 and Figure 5.4.10 shows the various stages and cases considered in this stratified model. At the start of a transient in which the core outlet temperature is dropping, the plume in the outlet plenum goes to the top of the plenum; and the outlet plenum is fully mixed, giving stage 1. As the core outlet temperature and velocity drop, the plume no longer reaches the top of the plenum. This leads to the start of stage 2 in which the outlet coolant goes to layer 1. In stage 2 the layer boundary is at the elevation of the core outlet. After enough cool liquid has entered layer 1 to fill one quarter of its volume, stage 3, case 3.1 begins. In this case, the plume coolant still goes to layer 1, but the interface between layers rises as liquid is added to layer 1. In this case, the plume also entrains hot liquid from the interface into layer 1. If the core outlet temperature at the start of the transient becomes hotter than the outlet plenum temperature, then stage 3, case 3.2 is entered. In this case, the core outlet coolant goes to a top hot layer, entraining cool outlet plenum liquid as it passes through. The three layer cases of stages 4 and 5 can occur in the later stages of a transient if the core outlet temperature starts out rising and later falls, or if the core outlet temperature starts out falling and later rises. If the coolant inlet into the volume is horizontal, as in the discharge of an IHX into a cold pool, then only stages 1, 3, and 5 are used.

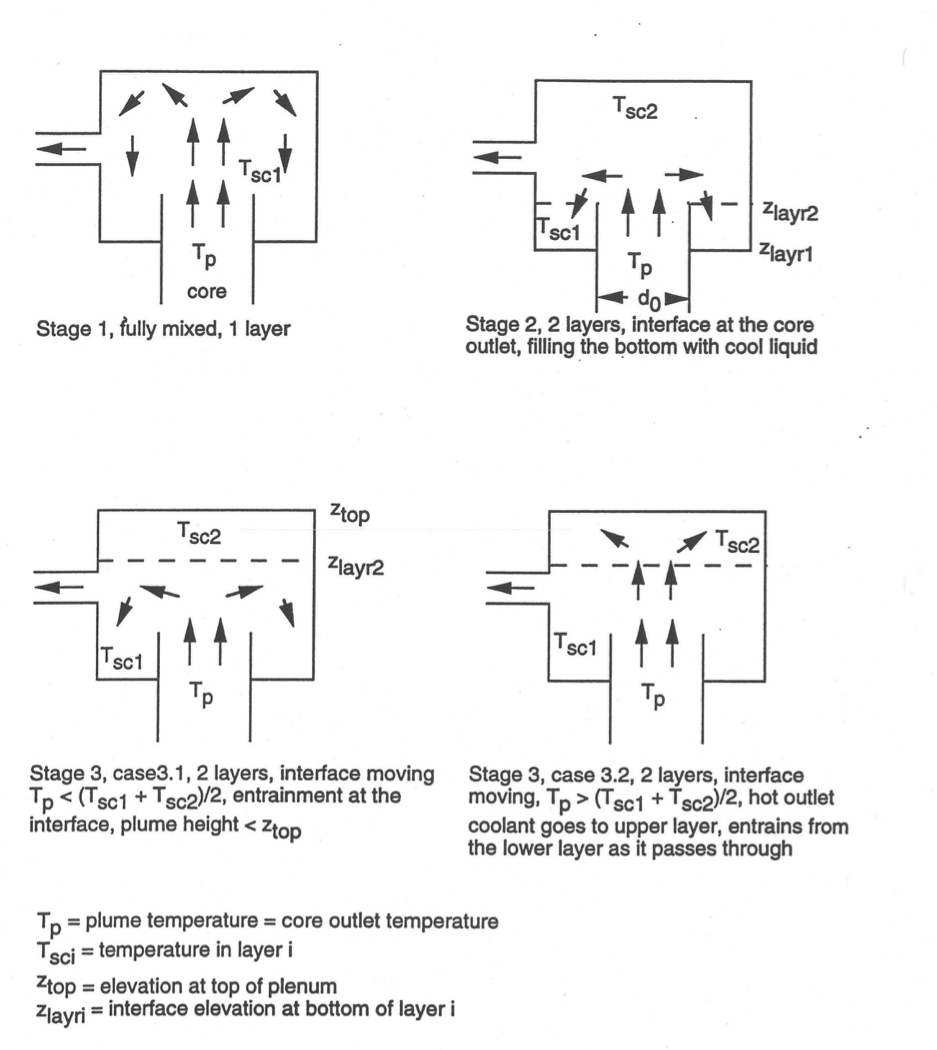
Figure 5.4.9 Stratified Volume Stages.

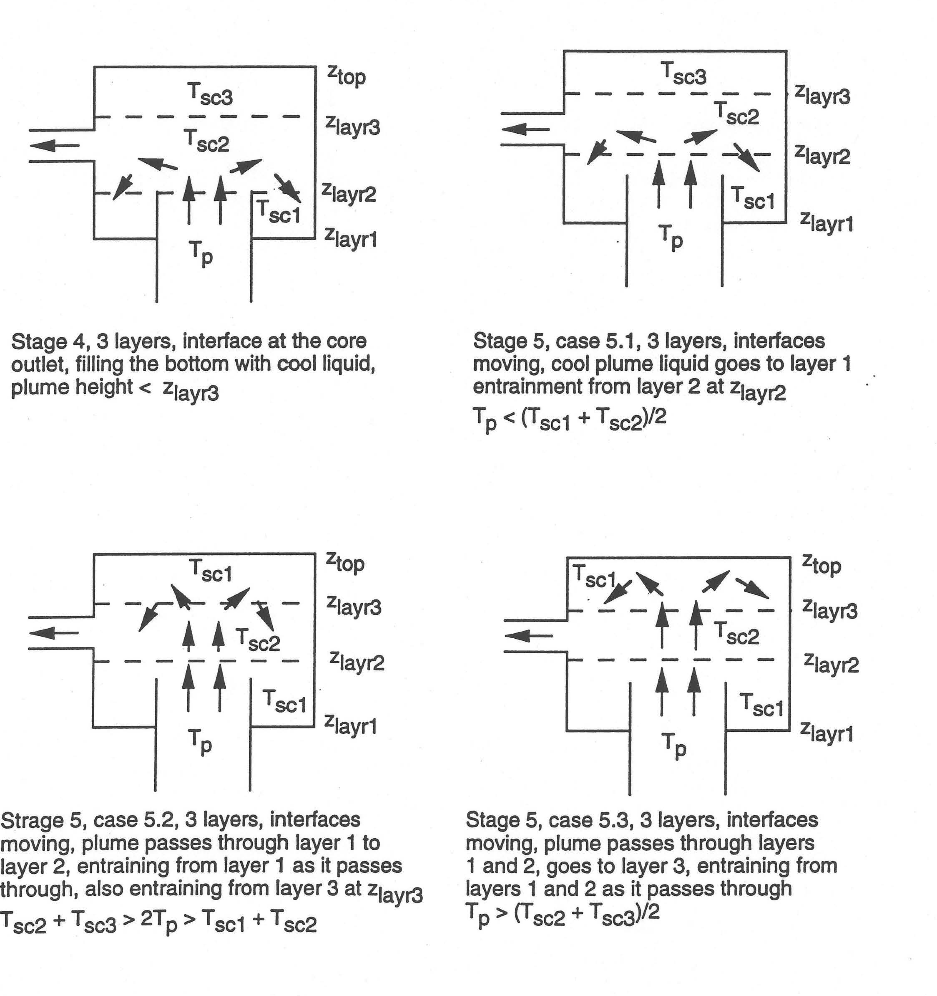
Figure 5.4.10 Stratified Volume Stages (Cont’d).

The jet height or plume height is calculated from an equation given by Yang [5‑8]:

(5.4-195)\[ h_{\text{jet}} = 1.0484 \text{Fr}^{0.785}\]

where

\(h_{\text{jet}}\) = height of the jet or the plane

(5.4-196)\[ \text{Fr} = \text{ Froude number } = \frac{v_{\text{o}}^{2} \rho_{\text{plume}}}{g~ r_{o}^{2} \left( \rho_{\text{plume}} - \rho_{\text{plenum}} \right)}\]

\(v_{\text{o}}\) = core exit velocity

\(\rho_{\text{plume}}\) = density of the plume

\(\rho_{\text{plenum}}\) = density of the plenum

\(r_{\text{o}}\) = core effective radius

\(g\) = acceleration of gravity

For entrainment at an interface, Howard and Lorenz give

(5.4-197)\[ w_{\text{ent}} = 0.2 \pi \rho_{\text{plume}} V_{\text{j}} d_{\text{j}}^2 F_{\text{f}}^{- 1.1}\]

where

\(v_{\text{j}}\) = plume average velocity at the interface and

\(d_{\text{j}}\) = plume effective diameter at the interface

\(w_{\text{ent}}\) = entrainment rate (kg/s).

The values of \(v_{\text{j}}\) and \(d_{\text{j}}\) depend on elevation and on whether the interface occurs within the zone of flow establishment or in the zone of established flow. The elevation change, \(z_{\text{o}}\), from the core outlet to the top of the zone of flow establishment is

(5.4-198)\[ z_{o} = \frac{r_{o}}{.111}\]

For \(z < z_{\text{o}}\), or the zone of flow establishment:

(5.4-199)\[ \frac{v_{\text{j}}}{v_{\text{o}}} = \frac{.25 + .02095 \left( \frac{z}{d}_{\text{o}} \right) + .003969 \left( \frac{z}{d}_{\text{o}} \right)^{2}}{\left\lbrack \frac{1}{2} + .1052\left( \frac{z}{d}_{\text{o}} \right) \right\rbrack^{2}}\]

and

(5.4-200)\[ \frac{d_{\text{j}}}{d_{\text{o}}} = 1 + .2104 \left( \frac{z}{d}_{\text{o}} \right)\]

For \(z > z_{\text{o}}\), or the zone of established flow,

(5.4-201)\[ \frac{v_{\text{j}}}{v_{\text{o}}} = \frac{2.018}{\frac{z}{d}_{\text{o}}}\]

and

(5.4-202)\[ \frac{d_{\text{j}}}{d_{\text{o}}} = .8649 \left( \frac{z}{d}_{\text{o}} \right)\]

For the wall temperatures, multi‑node treatments are used. The vertical wall around the outside of the outlet plenum or pool is treated with a number of vertical nodes. Each vertical node contains a number of lateral nodes, with coolant in contact with the first node. There is also an option to have another coolant compressible volume in contact with the last lateral node to account for heat transfer from a hot outlet plenum to a cold pool. The model has an option for a horizontal wall at the top or bottom of the plenum. This wall is handled with a 1‑D multinode treatment. Again, the first node is in contact with the plenum liquid, and the last node can be in contact with the coolant in another compressible volume.

The input for this model is as follows:

Table 5.4.20 Input for the Stratified Volume Model

Block	Location	Name	Meaning
3	1313	NSTRCV	Number of stratified compressible volumes
3	1314‑1316	ICVSTR(ICVST)	1 for vertical coolant inlet, as in an outlet plenum 2 for a horizontal coolant inlet
3	1320‑1322	NUMWAL(ICVST)	Number of wall sections
3	1323‑1325	IFSTWL(ICVST)	Wall number of the first wall section
3	1326‑1334	IWLHRZ(IW)	0 for a vertical wall 1 for a horizontal wall at the top of a CV 2 for a horizontal wall at the bottom of a CV
3	1335‑1343	NVNDWL(IW)	Number of vertical nodes in a vertical wall. NVNDWL = 1 for a horizontal wall
3	1344‑1352	NLNDWL(IW)	Number of lateral nodes in a wall section, Max. = 8
	Note: sum(NVNDWL*NLNDWL) <= 300.
3	1353‑1361	ICV2WL(IW)	Number of the CV in contact with the outer side of the wall section. = 0 for an adiabatic outer boundary. If ICV2WL > 38, ICV2WL = the temperature of a constant temperature heat sink.
3	1362	IDBSTR	Debug flag for stratified temperature model = 0, no debug prints = 1, final results only = 5, everything
3	1363	ISTDBS	PRIMAR time step when stratified debug starts.
3	1364	ISTSTP	Stop the run at PRIMAR step ISTSTP. Not used if ISTSTP = 0 or NSTRCV = 0.
3	1365	IFT16	Write out stratified CV output to STRATCV.dat every IFT16 PRIMAR steps. No output if IFT16 = 0.
18	5008	RCORE	Core radius for use in Froude number.
18	5009‑5017	HCSTWL(IW)	Coolant heat transfer coefficient at the inner surface of the wall section.
18	5027‑5035	ASTWL(IW)	Area of the wall section
18	5036‑5107	HINVWL(I,IW)	Thickness/thermal conductivity of node I in the wall section I = 1 - 8
18	5108‑5179	XMCSTW(I,IW)	Mass x heat capacity of node I in the wall.
18	5180‑5182	ZINST(ICVST)	z of inlet, used only for a vertical inlet. Otherwise ZOUTEL(IELL) is used.
18	5183‑5185	VOLBLI(ICVST)	Volume below the inlet, not used if there is a cover gas in the CV. In this case, the information is obtained from other input for the CV.
18	5186‑5188	EPSTST(ICVST)	Minimum temperature difference for switching stages.
18	5189‑5191	XLENTR(ICVST)	Entrainment length. A hot plume with a flow rate Wh, rising through a cool layer of thickness dz, will entrain cool liquid at a rate (dz/XLENTR) x Wh.