9.2. Model Formulation

9.2.1. Fuel Constituent Redistribution

Fuel constituent redistribution is one of the important characteristics of metallic fuel. Under a typical temperature gradient, three distinct radial regions form in the fuel [9‑1].

• A body centered cubic (BCC) single \(\gamma\) phase region forms in the central radial region.

• An effective dual phase structure forms in the middle radial region. This can approximately be characterized by tetragonal \(\beta\) precipitates and BCC \(\gamma\) phase regions.

• In the outer radial region, an approximate dual phase region forms, characterized by orthorhombic \(\alpha\) precipitates and BCC \(\delta\) phase regions.

Due to the difference of chemical affinity between the formed phase regions and zirconium and uranium atoms, radial migration of uranium and zirconium takes place. At equilibrium, zirconium-rich, uranium-depleted phases form in the central region, zirconium-depleted, uranium-rich phases form in the middle radial region, and a slightly zirconium-enriched region forms in the outer region. These structural and compositional changes affect fission gas behavior, porosity evaluation, fuel sintering behavior, solidus and liquidus temperature, fuel thermal conductivity, and radial power distribution.

A one-dimensional diffusion model based on thermo-transport theory is adopted to predict the fuel constituent redistribution. Based on experimental observations, it is assumed that: U and Zr atoms switch places, Pu is immobile, enthalpy of solution is negligible, and kinetic reactions terminate when a solubility limit is reached. Eq. (9.2-1) is used as the continuity equation for the Zr migration in metallic alloy fuel.

(9.2-1)\[\frac{du}{dt} = - \nabla \bullet \left( J_{D} + J_{T} \right)\]

where the diffusive transport in single-phase regions is given as:

(9.2-2)\[J_{D} = - D\nabla u\]

and the thermal transport term is given as follows:

(9.2-3)\[J_{T} = - \nabla T\frac{DQ}{RT^{2}}u\]

A summation over local phases is implied for thermal transport.

Axial migration is assumed to be negligible. In one-dimensional coordinates, Eq. (9.2-1) becomes:

(9.2-4)\[\frac{du}{dt} = \nabla \bullet \left\lbrack \left( D\nabla + \nabla T\frac{DQ}{R T^{2}} \right)u \right\rbrack = \frac{1}{r}\frac{d}{dr}\left ( rD\frac{du}{dr} + r\frac{dT}{dr}\frac{DQ}{RT^{2}}u \right)\]

where \(u\) is the Zr atom fraction, \(D\) is the Zr diffusion coefficient (m²/s), \(Q\) is the heat of transport of a local phase (J/mol), \(T\) is the temperature (K), \(R\) is the universal gas constant (J/mol/K), and \(r\) is the radial coordinate (m).

9.2.1.1. Numerical Solution

Utilizing a finite volume approach and applying the divergence theorem to Eq. (9.2-4), the following discretized equation for Zr atom fraction is obtained for the single-phase region:

(9.2-5)\[ \frac{d{\overline{u}}_{i}}{dt}\frac{r_{i + \frac{1}{2}}^{2} - r_{i - \frac{1}{2}}^{2}}{2} = \left\lbrack rD\frac{du}{dr} \right\rbrack_{r_{i - \frac{1}{2}}}^{ r_{i + \frac{1}{2}}} + \left\lbrack r\frac{dT}{dr}\frac{DQ}{RT^ {2}}u \right\rbrack_{r_{i - \frac{1}{2}}}^{r_{i + \frac{1}{2}}}\]

In two-phases regions, Fick’s Law does not apply and the diffusion term is neglected:

(9.2-6)\[ \frac{ d{\overline{u}}_{i}}{dt}\frac{r_{i + \frac{1}{2}}^{2} - r_{i - \frac{1}{2}}^{2}}{2} = \left\lbrack r\frac{dT}{dr}\frac{DQ}{RT^ {2}}u \right\rbrack_{r_{i - \frac{1}{2}}}^{r_{i + \frac{1}{2}}}\]

where \(i\) is the radial node, \(u\) is the Zr atom fraction, \(D\) is the Zr diffusion coefficient (m²/s), \(Q\) is the heat of transport (J/mol), \(T\) is the temperature (K), \(R\) is the universal gas constant, (J/mol/K), and \(r\) is the radial dimension (m).

For initial conditions, a uniform zirconium concentration is assumed based on user-defined input.

9.2.1.2. Boundary Conditions

Assuming no Zr leaves or enters at radial boundaries, the following boundary conditions are applied to the fuel inner and outer surfaces:

(9.2-7)\[ \frac{du}{dr} = 0\ \&\ Q = 0\ at\ r = 0\]

(9.2-8)\[ \frac{du}{dr} = 0\ \&\ Q = 0\ at\ r = R\]

where \(R\) is the fuel outer surface (m) and \(Q\) represents the heat of transport (J/mol) for each phase present at the corresponding boundary.

In the MFUEL model, Zr diffusion is bounded by the solubility limits of the phases present. To simplify the numerical solution while applying the solubility limit conditions, the following conditions are enforced:

(9.2-9)\[ \text{If: } u_{i} \geq u_{sol,\gamma}, u_{i + 1} \geq u_{sol,(\gamma\ or\ \delta)} \text{ Then: } Q_{\beta(i,i + 1)} = 0\]

(9.2-10)\[ \text{If: }u_{i} \geq u_{sol,\gamma},\ u_{i - 1} \geq u_{sol,\gamma} \text{ Then: } Q_{\gamma(i,i - 1)} = 0\]

(9.2-11)\[ \text{If: } u_{i} < u_{sol,\beta} \text{ Then: } {Q_{\gamma(i,i - 1)} = 0}{Q_{\beta(i,i + 1)} = 0}\]

(9.2-12)\[ \text{If: } u_{i} < u_{sol,\alpha} \text{ Then: } {Q_{\delta(i,i + 1)} = 0}{Q_{\alpha(i,i + 1)} = 0}\]

where \(u_{sol,\alpha}\), \(u_{sol,\beta}\), \(u_{sol,\delta}\), \(u_{sol,\gamma}\) are the solubility limits of \(\alpha,\beta,\delta,\gamma\) phases, respectively\(,\ {\ Q}_{\alpha(i,i + 1)}\), \(Q_{\beta(i,i + 1)}\), \(Q_{\delta(i,i + 1)}\) are the heat transport between cell \(i\) and \(i + 1\) for \(\alpha\), \(\beta\), and \(\delta\) phases, respectively, and \(Q_{\gamma(i,i - 1)}\) is the heat of transport between cell \(i\) and \(i - 1\) for the \(\gamma\) phase.

9.2.1.3. Time Step Control

In order to assure numerical convergence, the time step for the fuel constituent redistribution model is selected as a function of the fuel centerline temperature as given in Eq. (9.2-13).

(9.2-13)\[\begin{split}{\mathrm{\Delta}t}_{Zr} = min\left( \begin{cases} 50\ s & T_{c} \geq 1050\ K \\ 1000\ s & 900 \leq \ \ T_{c} < 1050\ K \\ 2000\ s & T_{c} < 900\ K \\ \end{cases} ,{\mathrm{\Delta}t}_{MFUEL}\ \right)\end{split}\]

where \({\mathrm{\Delta}t}_{MFUEL}\) is the MFUEL’s main time step, \({\mathrm{\Delta}t}_{Zr}\) is the selected time step for the Zr migration model, and \(T_{c}\) is the fuel centerline temperature (Kelvin). Section 9.3 describes MFUEL’s main time step for steady state and transients.

9.2.2. Fuel Clad Chemical Interaction

One of the constraints limiting metallic fuel performance is its chemical interaction with steel cladding. Its low solidus temperature combined with operation above the mid-point temperature of melting provides thermal activation for diffusion. During normal operation, migration of lanthanides from the fuel to the inner surface of the cladding leads to the formation of a brittle layer on this surface [9‑2]. In addition, diffusion of iron from the cladding to the fuel and formation of low melting temperature phases at the fuel surface occurs upon contact between the fuel and cladding. These iron-bearing phases may lead to eutectic formation during transients at elevated temperatures. Eutectic formation actuates the iron dissolution/penetration and can result in a significant amount of clad wastage [9‑3]. The lanthanide-rich, brittle layer and eutectic layer lead to clad thinning and embrittlement, which can result in creep fracture of the cladding.

9.2.2.1. Lanthanide Migration

Lanthanides are mostly insoluble within metallic fuels [9‑4]. Hence, it is assumed that they can be treated as diffusing in a single-phase medium. Having been produced by fission, the model allows lanthanides to diffuse under a concentration gradient. Lanthanide atoms that reach the unreacted cladding interface are assumed to precipitate in the form of \((Fe,Cr)_{17}{LA}_{2}\), consistent with experimental observations [9‑5].

The continuity equation for lanthanide migration in metallic alloy fuel is written as:

(9.2-14)\[ \frac{du}{dt} = - \nabla \cdot \mathbf{J}_{D} + q_{\text{La}}\]

where \(u\) is the atom density per unit volume (#/m³), \(\mathbf{J}_{D}\) is the diffusive transport current given in Eq. (9.2-2) , \(q_{\text{La}} = Y_{La}q^{'''}\) is the fission-produced lanthanide source term (#/m³/s), \(Y_{La}\) is the lanthanide yield per Joule, and \(q^{'''}\) is the power density, W/m^3.

In one-dimensional coordinates, the equation becomes as follows:

(9.2-15)\[ \frac{du}{dt} = D\nabla \cdot \nabla u + q_{\text{La}} = \frac{1}{ r}\frac{d}{dr}\left( rD\frac{du}{dr} \right) + Y_{La}q^{'''}\]

Initial lanthanide concentration is assumed to be zero for metal alloy fuel. Prior to the contact between the fuel and cladding, lanthanides are produced within the fuel but assumed to not be trapped in the fuel. Upon the formation of the contact between fuel and cladding, it is assumed that lanthanides diffuse to the cladding and form \((Fe,Cr)_{17}{LA}_{2}\) phase. At the interface between \((Fe,Cr)_{17}{LA}_{2}\) bearing clad layer and unaffected cladding, the boundary condition for the free lanthanide concentration is zero. The hard contact between the fuel and cladding initiates when the fuel outer surface reaches the inner clad surface where the brittle lanthanide layer presents. The brittle layer formed as a result of lanthanide diffusion is assumed not to bear any load. Hence, it is removed from the available cladding thickness during mechanical analysis.

9.2.2.2. Numerical Solution

Lanthanide diffusion is solved in the radial direction from fuel centerline to the outermost cladding cell in which lanthanides have migrated. Before contact is made between the fuel and the cladding, there is no lanthanide migration into the cladding. Once contact is made, lanthanides begin to diffuse into the inner-most cladding cell. Diffusion into subsequent (outward) cells is limited until a solubility limit is reached in the current, outermost cell. Once the outermost cell reaches saturation, diffusion can progress to the next outward cell. Using a finite volume approach and applying the divergence theorem, the following discretized equation is obtained for the lanthanide diffusion through the fuel and cladding:

(9.2-16)\[ \left( \frac{d{\overline{u}}_{i}}{dt} - q_{i} \right)\frac{r_{i + \frac{1}{2}}^{2} - r_ {i - \frac{1}{2}}^{2}}{2} = \left\lbrack rD\frac{du}{dr} \right\rbrack_{r_{i - \frac{1}{2}}}^{r_{i + \frac{1}{2}}}\]

where \(i\) is the radial cell, \(u\) is the La atom density (#/m³), \(q_{i}\) is the lanthanide production rate (#/m³/s), \(D\) is the La diffusion coefficient (m²/s), and \(r\) is the radial coordinate (m).

The production of lanthanides, \(q_{i}\), can be related to the fission power, \(P_{i}\), in a region of the core with Volume, \(V_{i}\). If the yield of lanthanides, \(y_{\text{La}}\), is defined per unit energy, the following equation is obtained:

(9.2-17)\[ q_{i} = y_{\text{La}}\frac{P_{i}}{V_{i}}\]

Prior to the pre-transient irradiation, MFUEL assumes there are no lanthanides in the fuel.

9.2.2.3. Boundary Conditions

(9.2-18)\[ \left. \ \frac{du}{dr} \right|_{r = 0} = 0\]

(9.2-19)\[ u\left( r = R_{\text{out}} \right) = 0\]

where \(R_{out}\) is the radial boundary between lanthanide-bearing and lanthanide-free cladding cells (m). Note that lanthanides that form compounds with the cladding are not counted as free lanthanide atoms, so there is a sink at the outer boundary. Once the lanthanide concentration at boundary node reaches the solubility limit, the corresponding node is assumed not to bear load (wastage) and the boundary node is shifted to the next cladding radial node.

9.2.2.4. Time Step Control

In order to assure numerical convergence, the time step for the lanthanide migration model is selected as a function of the fuel centerline temperature as given in Eq. (9.2-20).

(9.2-20)\[\begin{split}{\mathrm{\Delta}t}_{La} = min\left( \begin{cases} 50\ s & T_{c} \geq 1050\ K \\ 200\ s & 900 \leq \ \ T_{c} < 1050\ K \\ 500\ s & T_{c} < 900\ K \\ \end{cases} ,{\mathrm{\Delta}t}_{MFUEL}\ \right)\end{split}\]

where \({\mathrm{\Delta}t}_{MFUEL}\) is the MFUEL main time step, \({\mathrm{\Delta}t}_{La}\) is the selected time step for the lanthanide migration model, and \(T_{c}\) is the fuel centerline temperature (Kelvin). Section 9.3 describes MFUEL’s main time step for steady state and transients.

9.2.2.5. Iron Migration

Diffusion of iron into the fuel leads to formation of various complex phase structures at the fuel/clad interface. Experiments performed with U-10Zr/Fe-12Cr diffusion couples show that the main iron-bearing regions can be grouped into eight approximate regions, as given in Table 9.2.1 and depicted in Figure 9.2.1 [9‑6]. The maximum iron-bearing phase forms at the fuel/clad interface. As iron penetrates towards the fuel inner regions, the equilibrium iron concentration drops in each formed phase. In this work, each region is represented with its corresponding equilibrium iron concentration. Since the phases present are complex and uphill diffusion takes place, the diffusion of iron under the chemical potential gradient is modeled using regular solution theory. Thermodynamics and kinetics parameters is approximated based on available experimental data.

Table 9.2.1 Phase names, numbering, and approximate iron solubility

Phase Number	Phases	Approximate Iron Solubility limit (%)
0	Fuel	0
1	U-Pu-Zr matrix + U-Pu-23Zr-6Fe	2.5
2	U-Pu-Zr matrix+ U-Pu-42Zr-33Fe	13.2
3	(U,Pu)6Fe + U - 42Zr - 33Fe	21.8
4	(U,Pu)6Fe + U - 32Zr - 50 Fe	28.6
5	Fe2Zr + (U,Pu)6Fe	40.5
6	(U,Pu)Fe2` i	66.7
7	Clad	0.05 (lower limit)
8	Eutectic	50

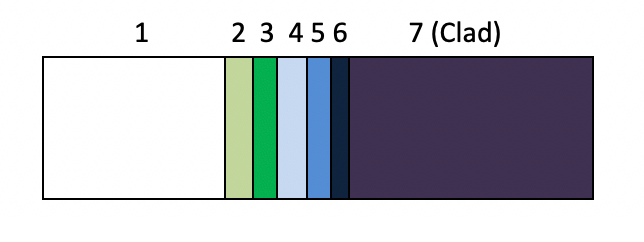
Figure 9.2.1 Phases formed at fuel cladding interface

The continuity equation for iron migration into metallic alloy fuel is defined as follows:

(9.2-21)\[ \frac{du}{dt} = - \nabla \cdot \mathbf{J}_{A}\]

where \(J_{A}\), the iron diffusion current (atom fraction*m/s), is given as follows:

(9.2-22)\[ J_{A} = - uM\nabla\mu\]

In one-dimensional coordinates, Eq. (9.2-21) becomes:

(9.2-23)\[ \frac{du}{dt} = \nabla \cdot uM\nabla\mu = \frac{1}{r}\frac{d}{dr}\left( ruM\frac{d\mu}{dr} \right)\]

where \(u\) is the iron atom fraction, \(\mu\) is the chemical potential of iron (J/mol), \(M = \frac{D}{RT}\) is the mobility, and \(D\) is the diffusion coefficient (m²/s), \(R\) is the universal gas constant (J/mol/K), and \(T\) is temperature (K).

The chemical potential is defined for each phase as:

(9.2-24)\[ \mu = W\left\lbrack (1 - u)^{2} - \left( 1 - C_{\text{sol}} \right)^{2} \right\rbrack\]

where \(W\) is the interaction parameter (J/mol) and \(C_{\text{sol}}\) (atom fraction) is the iron solubility limit.

With multiple (primary and forming) phases present, the chemical potential is defined as:

(9.2-25)\[ \mu = \sum_{m}^{}\mu_{m} = \sum_{m}^{}{f_{m}W_{m}\left\lbrack (1 - u)^{2} - \left( 1 - C_{\text{sol}}^{m} \right)^{2} \right\rbrack}\]

where \(f_{m}\) is the fraction of phase \(m\) present in the material.

When the solubility limit of a phase is exceeded, the supersaturation drives the growth of the new phase at the expense of the dissolution of the existing phase. The rate of phase growth under supersaturation is assumed to be temperature-dependent and modeled using the following equation:

(9.2-26)\[ \frac{\partial\eta_{m}}{\partial t} = k_{m0}\exp\left( - \frac{Q_{m}}{RT} \right)\]

where \(\eta_{m}\) is the phase fraction of phase \(m\), \(k_{m0}\) is the phase growth kinetics constant (1/s), \(Q_{m}\) is the activation energy (J/mol), \(R\) is the universal gas constant, (J/mol/K), and \(T\) is the temperature (K).

9.2.2.6. Numerical Solution

Iron migration is solved in radial coordinates between the fuel centerline and clad outer surface. The chemical interaction starts only if there is chemical contact between the fuel and cladding. Diffusion is assumed to take place under the chemical potential difference between radial cells.

Using a finite volume approach and applying the divergence theorem, the following discretized equation is obtained for the iron diffusion through fuel and cladding:

(9.2-27)\[ \frac{d{\overline{u}}_{i}}{dt}\frac{r _{i + \frac{1}{2}}^{2} - r_{i - \frac{1}{2}}^{2}}{2} = \lbrack ruM\nabla\mu\rbrack_{r_{i - \frac{1}{2}}}^{r_{i + \frac{1}{2}}}\]

where \(i\) is the radial cell, \(r\) is the radial location (m), \(u\) is the iron atom fraction, \(\mu\) is the chemical potential of iron (J/mol), \(M = \frac{D}{RT}\) is the mobility, \(D\) is the diffusion coefficient (m²/s), \(R\) is the universal gas constant (J/mol/K), and \(T\) is temperature (K).

Growth of the forming phase at a radial node-i using explicit time discretization of Eq. (9.2-26) as follows:

(9.2-28)\[ \frac{\eta_{mi}^{k} - \eta_{mi}^{ k - 1}}{\Delta t} = k_{m0}\exp\left( - \frac{Q_{m}}{RT} \right)\]

where \(\eta_{mi}^{k}\) and \(\eta_{mi}^{k - 1}\) are the phase fraction of \(m\)th phase for node-i at current and previous time steps, respectively, \(k_{m0}\) is the phase growth kinetics constant (1/s), \(Q_{m}\) is the activation energy (J/mol), \(R\) is the universal gas constant, (J/mol/K), and \(T\) is the temperature (K), \(\Delta t\) is the time step (s) .

Prior to the pre-transient irradiation, MFUEL assumes that there is no iron in the fuel and that the iron content in the cladding is uniform.

9.2.2.7. Boundary Conditions

(9.2-29)\[ \left. \ \frac{d\mu}{dr} \right|_{r = 0} = 0\]

(9.2-30)\[ \left. \ \frac{d\mu}{dr} \right|_{r = R} = 0\]

where \(R\) is the clad outer surface.

9.2.2.8. Time Step Control

In order to assure numerical convergence, the time step for the iron migration model is selected as a function of the fuel centerline temperature as given in Eq. (9.2-31).

(9.2-31)\[\begin{split}{\mathrm{\Delta}t}_{iron} = min\left( \begin{cases} 5\ s & T_{c} \geq 950\ K \\ 25\ s & 900 \leq \ \ T_{c} < 950\ K \\ 50\ s & 850 \leq \ \ T_{c} < 900\ K \\ 100\ s & T_{c} < 850\ K \\ \end{cases},{\mathrm{\Delta}t}_{MFUEL}\ \right)\end{split}\]

where \({\mathrm{\Delta}t}_{MFUEL}\) is the MFUEL main time step, \({\mathrm{\Delta}t}_{iron}\) is the selected time step for the iron migration model, and \(T_{c}\) is the fuel centerline temperature (Kelvin). Section 9.3 describes MFUEL’s main time step for steady state and transients.

9.2.2.9. Eutectic Formation

Above the fuel liquefaction temperature, eutectic formation and penetration into the cladding takes place via migration of actinides and iron at the fuel/cladding interface, resulting in liquefaction of the cladding. There are slow and rapid eutectic reactions. Ref. [9‑7] experimentally shows that metallic fuel liquefaction at temperatures below 1080°C is associated with the \((U,Pu)_{6}Fe\) phase, and the solubility limit of plutonium in this phase makes the transition plutonium dependent. As a result, the liquefaction for U-10Zr is assumed to take place at 715°C. The liquefaction temperature drops to 650°C for the U-19Pu-10Zr fuel alloy [9‑7]. Rapid eutectic formation is associated with melting of the \((U,Pu)Fe_{2}\) phase above 1080°C [9‑8].

There are two different eutectic formation models incorporated as part of this development, an empirical and a mechanistic model. The mechanistic model is applicable only to the slow eutectic formation and builds on top of the iron migration model. The empirical model covers both slow and rapid eutectic formation.

9.2.2.9.1. Mechanistic Eutectic Model

In the mechanistic model, slow eutectic formation at the fuel/cladding interface is activated once a threshold temperature is reached. Beyond this temperature, the mechanistic model accounts for actinide diffusion and eutectic phase formation by solving Eq. (9.2-23) and Eq. (9.2-26), respectively, in addition to iron diffusion. As actinides and iron diffuse towards the eutectic interphase, the supersaturation drives the eutectic growth towards the cladding.

9.2.2.10. Numerical Solution

Actinide migration is solved by a finite volume approach and applying the divergence theorem. The following discretized equation is obtained for actinide transport from fuel to the fuel-cladding interface:

(9.2-32)\[ \frac{d{\overline{u}}_{i}}{dt}\frac{r _{i + \frac{1}{2}}^{2} - r_{i - \frac{1}{2}}^{2}}{2} = \lbrack ruM\nabla\mu\rbrack_{r_{i - \frac{1}{2}}}^{r_{i + \frac{1}{2}}}\]

where \(i\) is the radial cell, \(r\) is the radial location (m), \(u\) is the actinide atom fraction, \(\mu\) is the chemical potential of actinides, (J/mol), \(M = \frac{D}{RT}\) is the mobility, and \(D\) is the diffusion coefficient, (m²/s), \(R\) is the universal gas constant (J/mol/K), and \(T\) is temperature (K).

When the solubility limit of actinides is exceeded, the supersaturation drives the growth of the eutectic phase into the next cell at the expense of the dissolution of the cladding. The rate of phase growth under supersaturation is assumed constant using Eq. (9.2-28) but with the parameters corresponding to the eutectic model.

9.2.2.11. Boundary Conditions

(9.2-33)\[ \left. \ \frac{d\mu}{dr} \right|_{r = 0} = 0\]

(9.2-34)\[ \left. \ \frac{d\mu}{dr} \right|_{r = R} = 0\]

where \(R\) is the clad outer surface (m).

9.2.2.11.1. Empirical Eutectic Model

The empirical model is based on Ref. [9‑8] and given in Eq. (9.2-35). This is the only model applicable to rapid eutectic formation, however, it also covers the slow eutectic formation range.

(9.2-35)\[\begin{split}E_{rate} = \begin{cases} C_{eut}\left(1.1338x10^{-9}\Delta T^{3} - 2.1522x10^{- 7}\Delta T^{2} \\ + 2.9265x10^{- 6}\Delta T + 9.22x10^{- 4} \right) & T_{low} < T < T_{high} \\ \left( \exp\left( 22.847 - \frac{27624}{T} \right) \right)x10^{- 6} & else \\ \end{cases}\end{split}\]

where \(T\) is Fuel Surface Temperature (K), \(\mathrm{\Delta}T = T - T_{peak}\) is the difference in temperature from the peak (K),\(E_{rate}\) is the eutectic formation rate (m/s),\(\ C_{eut}\) is a scaling factor which has been experimentally shown to depend on Pu content of the fuel, \(T_{low} = 1353.15\) is the lowest rapid eutectic formation temperature (K), \(T_{high} = 1506.15\) is the highest rapid eutectic formation temperature (K), and \(T_{peak} = 1388.15\) is the temperature at which peak eutectic formation rate occurs (K).

Similar to the lanthanide migration model, the eutectic layer is assumed not to bear any load in mechanical analysis.

9.2.2.12. Time Step Control

Since the eutectic model is active only during the transients, the time step for this model is equal to the MFUEL’s main time step.

9.2.3. Fuel Swelling and Fission Gas Release

Diffusion of fission gas atoms takes place up to the point where they get trapped by a sink such as phase boundaries, grain boundaries, dislocations, existing bubbles, or open porosity. The growth of bubbles is driven by gas diffusion, bubble coalescence, and operating conditions. Post-irradiation examination of high smear density EBR-II metal fuels [9‑9] indicates that a threshold gas swelling exists at approximately 10% gas swelling. Above the threshold gas swelling, fuel fracture and formation of interconnected open porosity network begins to take place. At this point, the gas in the fuel matrix or inside growing bubbles can be directly released to the plenum via interconnected porosity. After the formation of a significant amount of open porosity networks, gas swelling tends to saturate. However, solid fission product swelling continues. When hard contact (see Section 9.2.5) between fuel and cladding occurs, pressure sintering of the open porosity takes place to accommodate for solid fission product swelling.

Fission gas behavior models are based on the GRSIS algorithm developed by KAERI [9‑10] and further improved in the FEAST project at MIT [9‑11], [9‑12]. The model takes a similar approach to the FEAST code [9‑11], [9‑12] but is extended to account for the transient behavior, including fuel temperatures above the solidus temperature. A constant atom number bubble-grouping scheme is adopted considering morphological variation within the fuel due to formation of different phase structures. Bubbles in \(\alpha + \delta\) phase structure are treated as ellipsoidal whereas bubbles formed in \(\beta + \gamma\) and single \(\gamma\) phases are spherical. Three groups of closed bubbles (1: small, 2: medium, 3: large) and three groups of open porosity bubbles (4-1: connected small, 4-2: connected medium, 4-3: connected large) are modeled. Based on experimental observations in TREAT tests and furnace tests, large bubbles, which are 125 times larger than the medium bubble group, only occur at temperatures above the solidus temperature.

Fission gas atoms are generated by fission, and then form (nucleate) new bubbles or diffuse into existing bubbles. The bubbles are assumed to nucleate uniformly in the metallic fuel matrix due to the fact that they nucleate at both the grain boundaries and the phase boundaries, which are randomly distributed inside the grain. The closed bubbles can grow by trapping the diffusing fission gas atoms within the fuel matrix.

Open bubbles (or open pores) are chains of closed bubbles which have connected to each other and extend to the external free surface. When a closed bubble-i becomes an open porosity, it is transformed into bubble-4i. When the fuel matrix swelling due to the closed bubbles reaches the threshold value, it is assumed that a certain fraction of the bubbles become interconnected and release their gas into the free volume (i.e., they become open porosity). Open porosity bubbles are assumed not to exist until the threshold gas swelling, 10%, has been reached. Once the threshold has been reached, it is assumed that 1% of the closed bubbles create the open porosity network and gas release begins to take place.

9.2.3.1. Governing Equations

The mechanistic model consists of a set of equations for gas atoms in the fuel matrix, closed bubbles, open porosity and released gas to the interconnected porosity, and constitutive models for several reactions such as gas bubble nucleation, gas diffusion coefficients, bubble coalescence, etc.

Total fuel swelling is due to gas bubbles, open porosity, and solid fission products. The solid fission product swelling rate is set to 1.5%/ at% burnup. The total swelling is given as follows:

(9.2-36)\[ S_{0} = {\frac{\Delta V }{V_{0}} = N_{b1}V}_{1} + N_{b2}V_{2} + N_{b3}V_{3} + {N_{b4 1}V}_{1} + {N_{b42}V}_{2} + {N_{b43}V}_{3} + 0.015 \times bu\]

where Bu is the burnup (at %), \(S_{0}\) is the total fuel swelling (-) with respect to initial volume, \(V_{0}\) (\(m^{3}\)),\(\ N_{bi}\) is the density of closed bubble-i in the matrix (bubble/\(m^{3}\)),\(\ N_{b4i}\) is the density of porosity of type-i in matrix (bubble/\(m^{3}\)), and\(\ V_{i}\) is the volume of bubble-i (\(m^{3}\)/bubble-i).

The density of gas, closed bubbles, and open bubbles within the matrix is determined using:

Gas atom density in fuel matrix:

(9.2-37)\[ \frac{dC_{g}}{dt} = YF - \left ( J_{g1} + J_{g2} + J_{g3} + J_{g4} \right) - J_{b_{1},nucl}\]

Closed bubble density:

(9.2-38)\[\begin{split} \rho_{g1}\frac{dN_{b1}}{dt} = \left( J_{b_{1},nucl} + J_{g1} - \left( {ab}_{12} + {ab}_{13} \right) - \left( {gab}_{12} + {gab}_{21} + {gab}_{13} + {gab}_{31} \right) \\ - f_{12}\left( {ab}_{11} + {gab}_{11} \right) - {ab}_{14} - {gab}_{14} \right)\end{split}\]

(9.2-39)\[\begin{split} \rho_{g2}\frac{dN_{ b2}}{dt} = \left( J_{g2} + {ab}_{12} + {gab}_{12} + {gab}_{2 1} + f_{12}\left( {ab}_{11} + {gab}_{11} \right) - \left( {g ab}_{23} + {gab}_{32} \right) - \\ f_{23}\left( {ab}_{22} + {ga b}_{22} \right) - {ab}_{23} - {ab}_{24} - {gab}_{24} \right)\end{split}\]

(9.2-40)\[\begin{split} \rho_{g3}\frac{dN_ {b3}}{dt} = \left( J_{g3} + {ab}_{13} + {ab}_{23} + {gab}_{1 3} + {gab}_{31} + {gab}_{23} + {gab}_{32} + \\ f_{23}\left( {ab }_{22} + {gab}_{22} \right) - {ab}_{34} - {gab}_{34} \right)\end{split}\]

Open bubble density:

(9.2-41)\[ \rho_{g1}\frac{dN_{b41}}{dt} = {(ab}_{14} + {gab}_{14}) + \rho_{g1}\epsilon_{sint}N_{b41}\]

(9.2-42)\[ \rho_{g2}\frac{dN_{b42}}{dt} = ({ab}_{24} + {gab}_{24}) + \rho_{g2}\epsilon_{sint}N_{b42}\]

(9.2-43)\[ \rho_{g3}\frac{dN_{b43}}{dt} = ({ab}_{34} + {gab}_{34}\ ) + \rho_{g3}\epsilon_{sint}N_{b43}\]

Total gas release density:

(9.2-44)\[ \frac{dC_{gr}}{dt} = J_{g4} + {ab}_{14} + {ab}_{24} + {ab}_{34} + {gab}_{14} + {gab}_{24} + {gab}_{34}\]

where\(\ C_{g}\) is the gas atom concentration in the fuel matrix (atoms/\(m^{3}\)), Y is the fission yield of gas atoms, assumed to be 0.25 atoms/fission, F is the fission density with respect to the as-fabricated volume (fission/s/\(m^{3}\)), \(J_{gi}\) is the gas diffusion rate to bubble-i (atoms/\(m^{3}/s\)), \(J_{b_{1},nucl}\) is the Bubble-1 nucleation rate (atoms/\(m^{3}/s\)), \({ab}_{ij}\) is the transfer rate of bubble-i into bubble-j by bubble diffusion (atoms/\(m^{3}/s\)), \({gab}_{ij}\) is the transfer rate of bubble-i into bubble-j by radial growth of bubble-i (atoms/\(m^{3}/s\)), \(\epsilon_{sint}\) is the sintering strain rate on the fuel (1/s)\(,\) \(f_{i,i + 1}\) is the transition probability of bubble-i into bubble-(i+1) due to collision, and\(\ \rho_{gi}\) is the constant atom number per bubble-i.

Equilibrium bubble volume is determined based on Van der Waal’s equation:

(9.2-45)\[ \frac{V_{bei}}{\rho_{gi} } = B + \left\lbrack \left( \frac{\lambda\gamma}{kT} \right) \frac{1}{R_{ei}} + \frac{\sigma_{h}}{kT} \right\rbrack^{- 1}\]

where:

(9.2-46)\[ \sigma_{h} = - \frac{\sigma_{r} + \sigma_{\theta} + \sigma_{z}}{3}\]

and B is the Van der Waals Parameter (\(85 \times 10^{- 30}\) \(m^{3}/atom\)), \(\gamma = 0.8\) is the surface tension (N/m) [9‑13], \(R_{i} = \left( \frac{3V_{i}}{4\pi} \right)^{1/3}\)is the radius of bubble-i (m), \(\sigma_{h}\) is the hydrostatic stress, k= 1.3806\(\times 10^{- 23}\) is the Boltzmann constant (J/K), and \(\lambda\) is the bubble correction factor. For spherical bubbles, the value of \(\lambda\ \) is 2 [9‑14], but is reduced to 0.8 for ellipsoidal bubbles.

During pre-transient characterization, bubbles are assumed to be in equilibrium, \(V_{bi} = \ V_{bei}\). During the transients, non-equilibrium is assumed between the bubbles and the fuel matrix. It is assumed that bubble volume changes towards the equilibrium volume as a function of fuel creep as follows:

(9.2-47)\[ \frac{dV_{bi}}{dt} = V_{bi}\epsilon_{cr}\left( V_{bei} \right)\]

where \(\epsilon_{cr}\) is the fuel creep rate computed using pressure difference between matrix and bubble (1/s).

9.2.3.2. Numerical Solution

The fuel swelling and fission gas release model is a system of ordinary differential equations and is solved using a backwards Euler scheme. The system of ordinary differential equations is solved independently in every cell of the fuel. Prior to the pre-transient irradiation, MFUEL assumes there is no fission gas or porosity in the fuel. In order to ensure numerical stability, the time step used in this model is selected as a function of fuel temperature as given in Eq. (9.2-48). In single \(\gamma\) phase, larger diffusion coefficient dictates smaller time steps.

(9.2-48)\[\begin{split}{\mathrm{\Delta}t}_{fisg} = min\left( \begin{cases} 200\ s & T < T_{\gamma} \\ 100\ s & T \geq T_{\gamma} \\ \end{cases} ,{\mathrm{\Delta}t}_{MFUEL}\ \right)\end{split}\]

where \({\mathrm{\Delta}t}_{MFUEL}\) is the MFUEL coarse time step (s), \({\mathrm{\Delta}t}_{fisg}\) is the selected time step for the fuel swelling and fission gas release model (s), T is the fuel temperature (K), and \(T_{\gamma}\) is the single gamma phase transition temperature (K). Section 9.3 describes MFUEL’s main time step for steady state and transients.

9.2.4. Plenum Gas Pressure

The gas pressure in the free space of the fuel rod is computed assuming mechanical equilibrium and the ideal gas law. The initial fill gas, helium, is treated separately. The gas-filled plenum region and fuel’s interconnected open porosity network is the free space accommodating the released gas from the fuel and helium gas.

The plenum gas pressure is computed as follows:

(9.2-49)\[ P_{plegas} = \frac{N_{FGRel}RT_{ave}}{N_{A v}V_{tot}} + P_{0}\frac{T_{ave}}{T_{R}}\frac{V_{R}}{V_{tot}}\]

(9.2-50)\[ V_{tot} = V_{R} + \mathrm{\Delta}V_{ Plth} - \mathrm{\Delta}V_{Fuexp} + \mathrm{\Delta}V_{Fupor} + \mathrm{\Delta}V_{CladInnerExp} - \mathrm{\Delta}V_{NaExp}\]

(9.2-51)\[ T_{ave} = \frac{{V_{tot}T}_{plenum} + \sum_{j = 1}^{ mz}{\sum_{i = 1}^{nt}{T_{fuel}(i,j) \times V_{porg}(i,j)}}}{ V_{tot} + \sum_{j = 1}^{mz}{\sum_{i = 1}^{nt}V_{porg}}(i,j)}\]

where \(P_{plegas}\) is the plenum gas pressure (Pa), \(N_{FGRel}\) is the number of fission gas atoms released to the free space (-), \(N_{Av}\) is Avogadro’s number (-/mol), \(R\) is the universal gas constant (J/mol/K), \(T_{ave}\) is the average temperature of the overall free space (K), \(V_{tot}\) is the total available free space (m³), \(P_{0}\) is the initial fill-gas pressure (Pa), \(T_{R}\) is the reference temperature corresponding to the initial fill-gas pressure (K), and \(V_{R}\) is the reference volume corresponding to the initial fill-gas volume (m³).

Note that \(V_{tot}\) is determined based on the porosity of the fuel, expansion of the fuel and cladding, and relocation of the in-pin sodium (m³), where \(\mathrm{\Delta}V_{Plth}\) is the plenum region thermal expansion volume compared to as-fabricated dimensions (m³), \(\mathrm{\Delta}V_{Fuexp}\) is the fuel slug expansion (m³), \(\mathrm{\Delta}V_{Fupor}\) is the gas-filled fuel open porosity volume (m³), \(\mathrm{\Delta}V_{CladInnerExp}\) is the volume change due to clad inner radius expansion at fuel region (m³), and \(\mathrm{\Delta}V_{NaExp}\) is the volume change due to in-pin sodium expansion (m³). In Eq. (9.2-51), \(T_{plenum}\) is the plenum gas temperature(K), and \(T_{fuel}(i,j)\) and \(V_{porg}(i,j)\) are the fuel temperature (K) and gas filled porosity volume (m³) at a given radial and axial node (i,j).

Plenum gas pressure is computed at every time step directly by solving Eq. (9.2-49), Eq. (9.2-50), and Eq. (9.2-51), giving the plenum pressure at each time step.

9.2.5. Fuel Anisotropic Axial Elongation

Metallic fuels show anisotropic fuel axial elongation behavior. This is due to fuel cracking and irradiation growth/grain boundary tearing [9‑15]. After the fuel slug comes into soft contact with the cladding, further axial growth is restrained. Soft contact takes place when cracked fuel comes to radial contact with the cladding, whereas hard contact starts when the fuel swelling fills up all the cracks. Soft contact also activates the chemical contact between fuel and cladding. To incorporate this effect, the effective fuel slug radius is defined as follows:

(9.2-52)\[ r_{eff} = r_{0} + {dr}_{slug} + {dr}_{crack} = r_{slug} + {dr}_{crack}\]

where \(r_{0}\) is the as-fabricated fuel slug radius (m), \({dr}_{slug}\) is the radial strain increment due to thermal expansion, elasticity, creep, and swelling (m),\(\ r_{slug}\) is the current radial dimension without cracks/tears (m), and \({dr}_{crack}\) is the radius increment due to cracks and grain boundary tearing (m). Note that \({dr}_{crack}\) is not a physical boundary. It is only used to find out the contact condition between the fuel and cladding.

Fuel/cladding contact condition can be divided into three intervals:

\(r_{eff}\)< \(r_{c}\): No restraint by the cladding (no contact)

\(r_{slug}\)< \(r_{c}\) <\(r_{eff}\): Axial restraint by the cladding (soft contact)

\(r_{slug}\)= \(r_{c}\): Both radial and axial expansion restrained by the cladding (hard contact)

where \(r_{c}\) is the cladding radius.

\({dr}_{crack}\) is modeled empirically as a function of the as-fabricated gap, plutonium content, and peak linear heat rate to fuel diameter ratio (W/m²). The latter is a measure of temperature gradient:

(9.2-53)\[ {dr}_{crack} = f_{crack} \times {\mathrm{\Delta}r}_{gap0}\]

where \({\mathrm{\Delta}r}_{gap0}\) is the as-fabricated gap thickness (m) and \(f_{crack}\) is the axial anisotropy factor, modeled as a function of plutonium content and peak linear heat rate to fuel diameter ratio (W/m²) as shown in Figure 9.2.2.

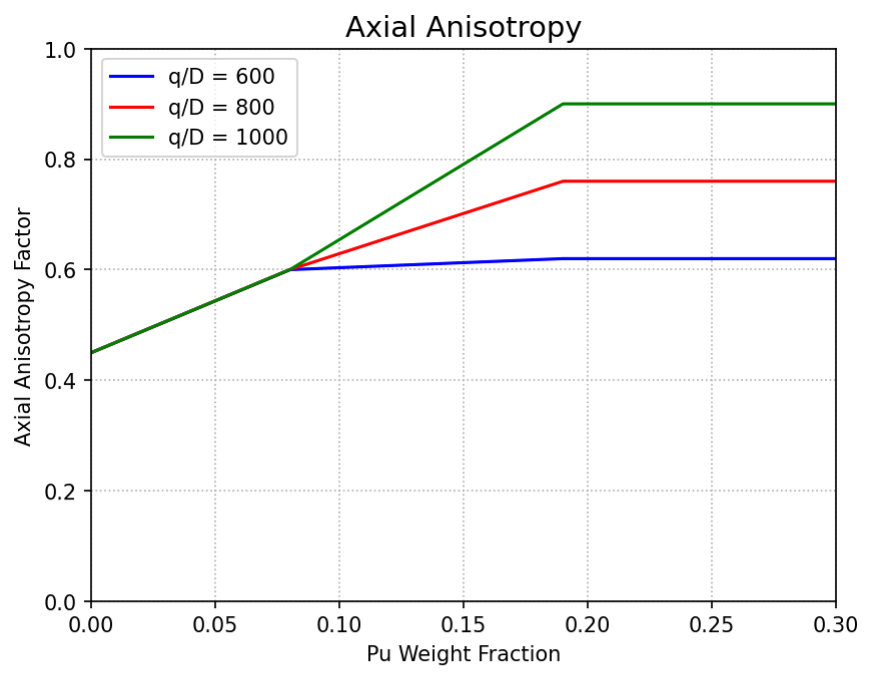
Figure 9.2.2 \(f_{crack}\) empirical parameter as a function of Pu content and peak linear heat rate to fuel diameter ratio

Fuel axial anisotropy factor is computed only once for each fuel channel during the steady state . Using the F parameter computed at peak power location within 0.5 at% peak burnup, the anisotropy factor is computed using the equations described in Table 9.2.2. The empirical model estimates at what fraction of the gap closure the soft contact will initiate. This value is assumed constant throughout the pre-transient characterization and transient simulations. The model is considered applicable for Pu contents between 0 to 26 wt%.

Table 9.2.2 Fuel axial anisotropy factor

Parameter	Pu < 0.08	0.08 ≤ Pu < 0.19	Pu ≥ 0.19
F < 700	\[\frac{0.15Pu} {0.08} + 0.45\]	\[\frac{0.02Pu} {0.11} + 0.60\]	\[0.62\]
700 ≤ F < 900	\[\frac{0.15Pu} {0.08} +0.45\]	\[\frac{Pu}{0.11} \left( 0.02 + 0.28\frac{F - 700}{200} \right) + 0.60\]	\[0.62 +0.28\frac{F- 700} {200}\]
F ≥ 900	\[\frac{0.15Pu} {0.08} +0.45\]	\[\frac{0.30Pu} {0.11} + 0.60\]	\[0.90\]

Where Pu is plutonium weight fraction, and \(F = \frac{Peak\ linear\ heat\ rate}{Initial\ Fuel\ slug\ diameter}\), W/cm²

9.2.6. Fuel Pin Mechanical Analysis

The mechanical analysis model is a 1.5-dimensional axisymmetric reduced order model based on assumptions of linear elasticity and incremental strain theory. A plane strain approach is applied to compute the axial displacements and thin shell theory is assumed to compute the cladding stresses. Furthermore, the fuel creep rate is assumed be high enough to avoid any significant buildup of stress gradient within the fuel slug.

Up until contact with the cladding, the fuel can freely swell in the axial and radial directions. Due to cracking and irradiation growth/grain boundary tearing, the fuel first comes to a soft contact with the cladding (see Section 9.2.5). During soft contact, the interfacial stress between the fuel and cladding is low, yet it is assumed to be high enough to limit axial elongation of the fuel. During pre-transient characterization, it is assumed that soft contact prevents the fuel from expanding axially, but allows the fuel to expand radially towards the available free space. In transient analysis, fuel in soft contact is assumed to be able to expand radially and axially.

When hard contact exists between the fuel and cladding, interfacial stresses build up to limit the fuel movement both axially and radially. As a result, the fuel slug becomes fully constrained by the cladding.

When the default model is used (IEUTOPT = 0 or 1), in the case of eutectic formation between the fuel and cladding, in the absence of hard contact at any axial node above, the soft and liquified fuel is allowed to expand primarily in the axial direction in a frictionless manner. When IEUTOPT = 2 or 3 options are selected, pore sintering upon eutectic formation is allowed. These options lead to less aggressive axial expansion.

Each time step, the model computes the axial and radial displacements of the fuel and cladding based on the contact status and the strain components. Radial displacement is computed as:

(9.2-54)\[ u_{r}(r) = \epsilon_{\theta}R_{in} + \int_{R_{in}}^{r}{\epsilon_{\theta}dr}\]

where \(u_{cr}\) is the radial displacement as a function of radial position (m), \(R_{in}\) is the inner radius of the structure (m), and \(\epsilon_{\theta}\) is the circumferential strain (m\(/\Delta\)m).

Axial displacement is computed as:

(9.2-55)\[ \epsilon_{z} = \frac{\partial u_{z}}{\partial z}\]

(9.2-56)\[ {\mathrm{\Delta}u}_{z}(r) = \epsilon_{z}(r)\mathrm{\Delta}z\]

(9.2-57)\[ \mathrm{\Delta}{\overline{u}}_{z} = \frac{1}{A}\int_{A}^{}{\Delta u}_{z}dA\]

(9.2-58)\[ {\overline{u}}_{z}(i) = \sum_{j = 1}^{i}{{\mathrm{\Delta}\overline{u}}_{z}(j)}\]

where \({\mathrm{\Delta}u}_{z}\) is the radial displacement as a function of radial position at a given axial node (m), \(\epsilon_{\theta}\) is the axial strain (m\(/\Delta\)m), \(\mathrm{\Delta}z\) is axial height at a given node (m), \(A\) is the cross-sectional area (\(m^{2}\)), \(\mathrm{\Delta}{\overline{u}}_{z}\) is the average axial displacement at a given axial node (m), and \({\overline{u}}_{z}(i)\) is the cumulative axial displacement at a given axial node I (m).

Strain is incremented based on the state of swelling, creep, thermal expansion, plenum pressure, and coolant pressure. Strain components are grouped into elastic and nonelastic contributions. Elastic and nonelastic strain components for fuel and cladding are conditional on the state of contact between the fuel and cladding. The strain on the fuel and cladding is described as:

(9.2-59)\[ \epsilon_{r} = \epsilon_{er} + \epsilon_{nr}\]

(9.2-60)\[ \epsilon_{\theta} = \epsilon_{e\theta} + \epsilon_{n\theta}\]

(9.2-61)\[ \epsilon_{z} = \epsilon_{ez} + \epsilon_{nz}\]

where:

(9.2-62)\[ \epsilon_{er} = \frac{1}{E}\left\lbrack \sigma_{r} - \nu\left( \sigma_{\theta} + \sigma_{Z} \right) \right\rbrack\]

(9.2-63)\[ \epsilon_{e\theta} = \frac{1}{E}\left\lbrack \sigma_{\theta} - \nu\left( \sigma_{r} + \sigma_{Z} \right) \right\rbrack\]

(9.2-64)\[ \epsilon_{ez} = \frac{1}{E}\left\lbrack \sigma_{z} - \nu\left( \sigma_{r} + \sigma_{\theta} \right) \right\rbrack\]

(9.2-65)\[ \epsilon_{nr} = \alpha(T - T_{0}) + \epsilon_{s} + \epsilon_{r}^{c}\]

(9.2-66)\[ \epsilon_{n\theta} = \alpha(T - T_{0}) + \epsilon_{s} + \epsilon_{\theta}^{c}\]

(9.2-67)\[ \epsilon_{nz} = \alpha(T - T_{0}) + \epsilon_{s} + \epsilon_{z}^{c}\]

where \(\sigma_{r},\sigma_{\theta},\sigma_{z}\) are the radial, azimuthal, and axial stress (Pa), \(\epsilon_{r},\epsilon_{\theta},\epsilon_{z}\) are the radial, azimuthal, and axial total strain components (m\(/\Delta\)m), \(\epsilon_{er},\epsilon_{e\theta},\epsilon_{ez}\) are the radial, azimuthal, and axial elastic strain components (m\(/\Delta\)m), \(\epsilon_{nr},\epsilon_{n\theta},\epsilon_{nz}\) are the radial, azimuthal, and axial non-elastic strain components (m\(/\Delta\)m), E is the Elastic Modulus (Pa), \(\nu\) is the Poisson’s ratio (-), \(\alpha\) is the linear thermal expansion coefficient (m\(/\Delta\)m-K), T is the material temperature (K), \(T_{0}\) is the reference temperature (K), \(\epsilon_{s}\) is the swelling strain (m\(/\Delta\)m), and \(\epsilon_{r}^{c}\),\(\ \epsilon_{\theta}^{c},\ \epsilon_{z}^{c}\) are the radial, azimuthal, and axial creep strain (m\(/\Delta\)m).

During pre-transient characterization, soft contact conditions are assumed to restrict movement in the axial direction. To account for this, the axial non-elastic strain components of the fuel are transferred to the radial and azimuthal directions as follows:

(9.2-68)\[ \epsilon_{r} = \epsilon_{er} + \epsilon_{nr} + 0.5\epsilon_{nz}\]

(9.2-69)\[ \epsilon_{\theta} = \epsilon_{e\theta} + \epsilon_{n\theta} + 0.5\epsilon_{nz}\]

(9.2-70)\[ \epsilon_{z} = \epsilon_{ez}\]

Similarly, when the fuel and cladding are subject to hard contact conditions and all of the fuel slugs above the current elevation have formed a eutectic, the default model (IEUTOPT = 0 or 1) assumes that strain in the axial direction is dominant. To account for this, the radial and azimuthal non-elastic strain components of the fuel are transferred to the axial directions as follows:

(9.2-71)\[ \epsilon_{r} = \epsilon_{er}\]

(9.2-72)\[ \epsilon_{\theta} = \epsilon_{e\theta}\]

(9.2-73)\[ \epsilon_{z} = \epsilon_{ez} + \epsilon_{nz} + \epsilon_{nr} + \epsilon_{n\theta}\]

Users may skip this model and use Eq. (9.2-41) through Eq. (9.2-43) if IEUTOPT is set to 2 or 3.

9.2.6.1. Fuel Stress

Fuel stress is computed using a reduced order model. The reduced order model assumes no stress gradient within the fuel or the cladding. Prior to hard contact, the fuel stress distribution at a given axial location is given as follows:

(9.2-74)\[ \sigma_{fr} = \sigma_{f\theta} = {- P}_{Plgas}\]

(9.2-75)\[ \sigma_{fz} = {- (P}_{Plgas} + P_{fw})\]

where \(\sigma_{fr}\),\(\ \sigma_{f\theta}\),\(\ \sigma_{fz}\) are the fuel radial, azimuthal, and axial stress (Pa), \(P_{Plgas}\) is the plenum gas (Pa), and \(P_{fw}\) axial force due to fuel weight on the fuel surface (Pa).

Upon formation of the hard contact between the fuel and cladding, the primary mechanism balancing any fuel axial expansion is porosity sintering or hot pressing, which is assumed to be isotropic. The interfacial stress is computed such that the fuel outer and clad inner displacements are aligned as shown in Eq. (9.2-76).

(9.2-76)\[ u_{fr}|_{outer} \cong u_{cr}|_{inner} \& u_{fz}|_{outer} \cong u_{cz}|_{inner}\]

(9.2-77)\[ \sigma_{fr} = \sigma_{f\theta} = \sigma_{fz} = \sigma_{contact}\]

Contact stress is computed in a stepwise manner such that every time step its value is allowed to increase or decrease incrementally towards the equilibrium value. Default stress step size is 0.1 MPa. However, if the expansion or contraction rate requires larger step size, the stress step is increased to 1 MPa. This relaxation ensures numerical convergence without disrupting the accuracy.

9.2.6.2. Clad Stress

Cladding stress is assumed using a thin shell theory based on the applied stress at the inner and outer surface. The thin shell theory equations used to calculate the cladding principal stress are:

(9.2-78)\[ \sigma_{cr} = \frac{\sigma_{inner\ R} + \sigma_{outer\ R}}{2}\]

(9.2-79)\[ \sigma_{c\theta} = - \frac{{(\sigma}_{inner\ R} - \sigma_{outer\ R})R_{c}}{\Delta r}\]

(9.2-80)\[ \sigma_{cz} = - \frac{{(\sigma}_{inner\ R} - \sigma_{outer\ R})R_{c}}{2 \times \Delta r}\]

where \(\sigma_{cr},\sigma_{c\theta},\sigma_{cz}\) is the clad radial, hoop, and axial stress (Pa), \(\sigma_{inner\ R}\) is the contact stress between fuel and cladding (Pa), \(\sigma_{outer\ R}\) is the coolant pressure, and \(\Delta r\) is the current active clad thickness (m), where the clad wastage has been subtracted as it is assumed to not bear any load.

9.2.6.3. Fuel Swelling Strain

Fuel swelling strain is the largest in magnitude compared to other strain components (see Section 9.2.3). In order to be compliant with the incremental strain theory and the reduced order modeling approach, fuel swelling strain is first radially averaged for a given time step, and the average radial value is used to determine the axial displacements, shown in Eq. (9.2-81):

(9.2-81)\[ \epsilon_{s} = \frac{\overline{S}}{3}\]

(9.2-82)\[ \overline{S} = \frac{1}{V}\int_{V}^{}{S\ dV} = \frac{1}{V}\int_{V}^{}{\frac{S_{0}}{\left( 1 + S_{0} + 3\alpha(T - T_{R}) \right)}dV}\]

where \(\epsilon_{s}\) is the average linear swelling strain (-), \(\overline{S}\) is the radial average volumetric swelling with respect to the current fuel dimensions (-), \(S_{0}\) is the local fuel swelling with respect to the fresh fuel dimensions (-), \(S\) is the local fuel swelling with respect to the current fuel dimensions (-), and V is the fuel volume of the axial zone (m³).

Following the radial displacement of the nodes using Eq. (9.2-54), the radial positions are corrected using the local swelling strain:

(9.2-83)\[ A_{i}^{c} = A_{i}\frac{1 + S}{1 + \overline{S}}\]

(9.2-84)\[ R_{i} = \sqrt{A_{i,c}\frac{\sum_{j = 1}^{i}A_{j}}{\sum_{j = 1}^{i}A_{j}^{c}} + R_{i - 1}^{2}}\]

where \(A_{i}\) is the node area (m²), \(A_{i}^{c}\) is the corrected node area accounting for difference between average and local swelling strain (m²), and \(R_{i}\) and \(R_{i - 1}\) are the radial location for node-i and node-(i-1), respectively (m).

9.2.6.4. Clad Swelling Strain

For a given axial node, clad swelling strain is computed using the average clad temperature, neutron flux, and neutron fluence. In order to comply with the incremental strain theory approach, the incremental swelling strain at a given time step is adjusted to reflect the current volume:

(9.2-85)\[ \epsilon_{s} = \frac{\overline{S_{0}}}{3\left( 1 + \overline{S_{0}} + 3\alpha(T - T_{R}) \right)}\]

\[\overline{S_{0}} = f(T,\phi,\psi)\]

where \(T\) is the temperature at the clad midwall (K), \(\phi\) is the neutron flux (#/cm²-s), \(\psi\) is the neutron fluence (#/cm²), \(\epsilon_{s}\) is the linear incremental swelling strain with respect to the current volume (-), and \(\overline{S_{0}}\) is the volumetric incremental swelling strain with respect to the as-fabricated volume (-).

9.2.6.5. Fuel Creep Strain

Metal fuel typically operates with a high creep rate due to its porous nature and low fuel solidus temperature. As a result, reduced order mechanical analysis models are more appropriate than full elastoplastic solutions with Finite Element (FE) or Finite Volume (FV) approaches considering computational efficiency versus accuracy. MFUEL accounts for the creep strain as the driving force for the pore sintering, which is an essential component to drive the fuel and cladding displacements, as well as stresses. Therefore, creep terms within the fuel, with the exception of hot pressing, are set to zero.

(9.2-86)\[ \epsilon_{r}^{c} = \epsilon_{\theta}^{c} = \epsilon_{z}^{c} = 0.0\]

Hot pressing strain is defined as a function of equivalent creep strain [9‑9]. If the average stress on fuel matrix is greater than the gas pressure, the sintering strain is non-zero. Otherwise, sintering rate is set to zero. Moreover, in order to account for fission-driven creep, the minimum fuel temperature used to compute the creep rate is set to 800 K. This is consistent with transition from thermal to radiation enhanced diffusion at about half of the fuel solidus temperature [9‑14]:

(9.2-87)\[ \epsilon_{sint} = \alpha_{p}\epsilon_{eq}\]

\[\begin{split}\epsilon_{eq} = \begin{cases} \left( 5x10^{3}\sigma_{hp} + 6\sigma_{hp}^{4.5} \right)e^{- \frac{26170}{T}}, & phase\ \neq Gamma \\ 0.08\sigma_{hp}^{3}e^{- \frac{14350}{T}}, & phase = Gamma \\ \end{cases}\end{split}\]

\[\begin{split}\sigma_{hp} = \begin{cases} 0.0, & - \frac{\sigma_{r} + \sigma_{\theta} + \sigma_{z}}{3x10^{6}} \leq P_{plegas}\ \\ \left| - \frac{\sigma_{r} + \sigma_{\theta} + \sigma_{z}}{3x10^{6}} - \frac{P_{plegas}}{1x10^{6}} \right|, & - \frac{\sigma_{r} + \sigma_{\theta} + \sigma_{z}}{3x10^{6}} > P_{plegas} \\ \end{cases}\end{split}\]

\[\begin{split}\alpha_{p} = \begin{cases} 0.0, & V_{4} \leq 0.0\ \\ \frac{C}{6}\left( \frac{V_{4}}{0.1} \right)^{1.5}, & 0.0 < V_{4} < 0.1 \\ \frac{C}{6}, & V_{4} > 0.1 \\ \end{cases}\end{split}\]

\[{V_{4} = N_{b41}V}_{1} + {N_{b42}V}_{2} + {N_{b43}V}_{3}\]

where \(T\) is the temperature of the fuel (K), \(\epsilon_{eq}\) is the equivalent strain rate (-), \(\sigma_{r},\sigma_{\theta},\sigma_{z}\) are the principle stresses in r, \(\theta\), z directions, respectively (Pa), \(V_{4}\) is the open porosity swelling (m³) (see Section 9.2.3), \(\alpha_{p}\) is the pore compressibility factor (-), and C is the empirical constant, set to 10 (-).

If the hydrostatic stress is higher than the fuel porosity sintering yield strength, pore sintering is computed using yield conditions (Section 9.8.5).

9.2.6.6. Clad Creep Strain

Clad creep strain primarily consists of irradiation and thermal components. The creep strain in r, \(\theta\), and z direction is computed using an equivalent strain and stress:

(9.2-88)\[ \epsilon_{r}^{c} = \frac{\epsilon_{eq}}{\sigma_{eq}}\left( \sigma_{r} - 0.5 \left( \sigma_{\theta} + \sigma_{z} \right) \right)\Delta t\]

\[\epsilon_{\theta}^{c} = \frac{\epsilon_{eq}}{\sigma_{eq}}(\sigma_{\theta} - 0.5\left( \sigma_{r} + \sigma_{z} \right))\Delta t\]

\[\epsilon_{z}^{c} = \frac{\epsilon_{eq}}{\sigma_{eq}}(\sigma_{z} - 0.5\left( \sigma_{r} + \sigma_{\theta} \right))\Delta t\]

\[\epsilon_{eq} = g\left( T,\phi,\sigma_{eq} \right) + h\left( T,t,\sigma_{eq} \right)\]

\[\sigma_{eq} = \frac{1}{2}\left( \left( \sigma_{r} - \sigma_{\theta} \right)^{2} + \left( \sigma_{r} - \sigma_{z} \right)^{2} + \left( \sigma_{\theta} - \sigma_{z} \right)^{2} \right)^{0.5}\]

where \(T\) is the temperature at the inner surface of the cladding (K), \(\phi\) is the neutron flux (#//cm²-s), \(\epsilon_{eq}\) is the equivalent creep strain rate (1/s), \(\sigma_{eq}\) is the equivalent stress rate (Pa) , \(g\left( T,\phi,\sigma_{eq} \right)\) is an empirical function capturing the irradiation creep strain rate, and \(h\left( T,t,\sigma_{eq} \right)\) is an empirical function capturing the thermal creep strain rate.

9.2.6.7. Numerical Solution

At each time step, the model updates the contact state between the fuel and cladding and contact pressure using previous time step nodal positions. Then the model determines the elastic and non-elastic strain components in each radial node of the fuel and cladding.

Incremental strain components, \({\mathrm{\Delta}\epsilon}_{r,i}^{t}\), \({\mathrm{\Delta}\epsilon}_{\theta,i}^{t}\), \({\mathrm{\Delta}\epsilon}_{z,i}^{t}\), for radial node \(i\) are computed as follows:

(9.2-89)\[ {\mathrm{\Delta}\epsilon}_{r,i}^{t} = \epsilon_{r,i}^{t} - \epsilon_{r,i}^{t - 1}\]

(9.2-90)\[ {\mathrm{\Delta}\epsilon}_{\theta,i}^{t} = \epsilon_{\theta,i}^{t} - \epsilon_{\theta,i}^{t - 1}\]

(9.2-91)\[ {\mathrm{\Delta}\epsilon}_{z,i}^{t} = \epsilon_{z,i}^{t} - \epsilon_{z,i}^{t - 1}\]

9.2.6.8. Fuel displacements

The radial and axial fuel displacements are computed using linear elasticity and strain/displacement relationships:

(9.2-92)\[ u_{r,i}^{t} = \sum_{i^{'} = 1}^{i}{{\mathrm{\Delta}\epsilon}_{\theta,i^{'}}^{t}(R_{i^{'} + 1}^{t} - R_{i^{'}}^{t})}\]

(9.2-93)\[ \mathrm{\Delta} u_{z,j}^{t} = \frac{1}{A_{f}}\sum_{i = 1}^{NT}{{\mathrm{\Delta }\epsilon}_{z,i}^{t}\mathrm{\Delta}z_{j}\mathrm{\Delta}A_{fi}}\]

(9.2-94)\[ {\overline{u}}_{z ,j}^{t} = \sum_{j^{'} = 1}^{j}{\mathrm{\Delta}u}_{z,j^{'}}^{t}\]

where \(u_{r,i}^{t}\) is the radial displacement at node \(i\) at time \(t\), \(\mathrm{\Delta}u_{z,i}^{t}\) is the axial displacement computed using plain strain assumption, \(\mathrm{\Delta}A_{fi}\) is the cross-sectional area of node \(i\), \(A_{f}\) is the total fuel cross-sectional area, and \(NT\) is the number of radial nodes in the fuel. The cumulative value of the axial displacements is computed by Eq. (9.2-58) for axial node \(j\).

If the eutectic forms between the fuel and cladding at hard contact condition, contact pressure is set to the plenum pressure. As a result the constraint keeping the fuel and cladding interface is lost. To correct for this, if the fuel boundary exceeds the clad boundary, the following correction is applied to the computed radial node positions:

(9.2-95)\[ area\_ ex = \frac{R_{ci}^{2}}{R_{fo}^{2}}\]

(9.2-96)\[ R_{i} = \sqrt{R_{i0}^{2} \times area\_ ex}\]

Where \(area\_ ex\) is the area fraction that fuel will be contracted radially if the conditions are met (m²), \(R_{ci}\) and \(R_{fo}\) are clad inner and fuel outer radius (m). \(R_{i0}\) and \(R_{i}\) are the fuel radial node positions (m) for previous and current time steps, respectively.

9.2.6.9. Clad Displacements

The radial and axial clad displacements are computed using linear elasticity and strain/displacement relations:

(9.2-97)\[ u_{cr,i}^{t} = {\mathrm{\Delta}\epsilon}_{\theta,NE}^{t} R_{NE}^{t} + \sum_{i^{'} = NE}^{NE + i - 1}{{\mathrm{\Delta}\epsilon}_{\theta,i^{'}}^{t}(R_{i^{'} + 1}^{t} - R_{i^{'}}^{t})}\]

(9.2-98)\[ \mathrm{\Delta}u_{cz,j}^{t} = \frac{1}{A_{c}}\sum_{i^{'} = NE}^{NE + n - 1}{{\mathrm{\Delta}\epsilon}_{z,i^{'}}^{t}\mathrm{\Delta}z_{j}\mathrm{\Delta}A_{ci^{'}}}\]

(9.2-99)\[ {\overline{u}}_{z,j}^{t} = \sum_{j^{'} = 1}^{j}{\mathrm{\Delta}u}_{z,j^{'}}^{t}\]

where \(u_{cr,i}^{t}\) is the radial displacement of node \(i\) (m) at time \(t\), \(\mathrm{\Delta}u_{cz,j}^{t}\) is the axial displacement (m) computed using plain strain assumption, \(\mathrm{\Delta}A_{ci}\) is the cross-sectional area of node \(i\)(m²), \(A_{c}\) is the total clad cross-sectional area(m²), \(R_{NE}^{t}\) is the clad inner radius (m) at time \(t\), and \(n\) is the number of nodes in the cladding. The cumulative value of the axial displacement is computed by Eq. (9.2-58) for axial node \(j\).

9.2.7. In-Pin Sodium Treatment

The in-pin sodium bond between the fuel and the cladding will relocate during irradiation. As the fuel swells, the bond sodium is primarily pushed to the top of the fuel column, reducing the available gas volume. In addition, as the interconnected porosity forms, bond sodium can infiltrate into some of the open porosity, leading to significant changes in fuel thermal conductivity. The sodium infiltration primarily takes place at the fuel outer region where \(\alpha + \zeta + \delta\) phases exist and larger lenticular bubbles and cracks form. In \(\beta + \zeta + \delta\) phase, bubbles are rather small, hindering sodium infiltration.

The porosity fraction that is filled by sodium is computed using the following relations in the \(\alpha + \zeta + \delta\) phase region for fuel nodes that are radially located beyond 60% of the fuel radius:

(9.2-100)\[\begin{split}P_{Na,fr} = \begin{cases} 0.6 & contact \neq hard \\ max(0.3,\ 0.6 - 5(B - B_{0})) & contact = hard \\ \end{cases}\end{split}\]

where:

\(P_{Na,fr}\): Fraction of the fuel porosity that is filled by sodium. Minimum allowed value is 0.3 for \(\ \alpha + \zeta + \delta\) phase and for the fuel radial location that is greater than 60% of the fuel radius

\(B\): Burnup (atom fraction)

\(B_{0}\): Burnup at which the fuel and clad hard contact initiated (atom fraction)

If the fuel is not \(\alpha + \zeta + \delta\) phase or the radial location is less than 60% of the fuel radius, it is assumed there is no sodium infiltration. This assumption is based on experimental data given in Ref. [9‑16].

At each time step during pre-transient characterization, the movement of sodium within the pin is updated as a function of phases present in the fuel, burnup, and the width of the fuel/cladding gap in an explicit manner. This information is used to compute the fuel thermal conductivity and plenum pressure. In transient, the sodium infiltrated into fuel porosity is not updated and assumed immobile.

9.2.8. Clad Outer Corrosion

Although stainless steel and sodium coolant have excellent compatibility, the minor corrosion that takes place is modeled empirically based on Ref. [9‑17] using the following equation:

(9.2-101)\[ \frac{dr}{dt} = 3.310^{- 6}\exp\left( - \frac{133031.4}{RT} \right)\]

where \(\frac{dr}{dt}\) is the corrosion rate (m/s), \(R\) is the universal gas constant (J/mol/K), \(T\) is the clad outer temperature (K).

The corrosion thickness is solved at each axial node using a backward Euler method.

9.2.9. CDF-Based Clad Creep Rupture

Creep-induced nucleation and diffusion growth of the grain boundary cavities are the primary failure mechanisms of commercial steels being used as the cladding material. The mechanism is called “intergranular creep fracture.” The complex phenomenon shows strong dependency on the present microstructure. The carbide/sulfide particles at the grain boundaries and their precipitation/coarsening or dissolution behavior, grain size, dislocation loop density, dislocation dynamics, crystallographic orientation, and diffusivity are the essential parameters affecting the progression of event. Furthermore, history of the operation during normal operation, anticipated transients, or accident scenarios could also affect the cavity dynamics by large. If excessively thick and brittle phases form at the clad inner surface, the stress concentrations may arise and present additional components limiting the life of the fuel pin and complicating the problem further.

The high complexity of the underlying physics has forced engineers to adopt simple empirical models to predict the clad failure, such as the Cumulative Damage Fraction (CDF) model. The CDF model uses the available clad failure data generated under constant stress and constant temperature conditions. Rupture time is predicted by the following equation when CDF reaches unity:

(9.2-102)\[ CDF = \int_{0}^{t_{f}}\frac{dt}{t_{r}\left( \sigma_{\theta},T \right)} < 1\]

where \(t_{r}\) is the rupture time (hr), \(t_{f}\) is the final time (hr), \(\sigma_{\theta}\) is the hoop stress (Pa), and T is the temperature (K). Note that time to rupture correlations are derived from constant stress experiments whereas in simulation the magnitude of stress may change.

This development introduces CDF models for HT9 and D9 cladding. At this time, only the HT9 CDF model is applicable to the pre-transient fuel characterization.

9.2.9.1. HT9 CDF Model

The HT9 CDF model determines the rupture time based on the temperature and stress. At low temperatures, T <= 973.15 K, the rupture time is determined using:

(9.2-103)\[\begin{split}\log t_{r} = \begin{cases} \log t_{rs} & \sigma_{\theta} \leq \sigma_{ss} \\ \frac{\sigma_{\theta} - \sigma_{ss}}{\sigma_{tr} - \sigma_{ss}}(\log t_{rt} - \log t_{rs}) + \log t_{rs} & \sigma_{ss} < \sigma_{\theta} < \sigma_{tr} \\ \log t_{rt} & \sigma_{\theta} \geq \sigma_{tr} \\ \end{cases}\end{split}\]

(9.2-104)\[ \sigma_{ss} = 670.0 - 0.7(T - 273.15)\]

(9.2-105)\[ \sigma_{tr} = 1370.0 - 1.7(T - 273.15)\]

When the cladding temperature is between 973.15 K and 1042.15 K, the rupture time is determined using:

(9.2-106)\[\begin{split}\log t_{r} = \begin{cases} \frac{T - 973.15}{T_{ri} - 973.15}(\log t_{rt} - \log t_{rs}) + \log t_{rs} & \sigma_{\theta} \leq \sigma_{tr} \\ \log t_{rt} & \sigma_{\theta} \geq \sigma_{tr} \\ \end{cases}\end{split}\]

(9.2-107)\[ T_{ri} = \frac{2000 - \sigma_{\theta}}{2.6} + 273.15\]

(9.2-108)\[ \sigma_{tr} = 2000 - 2.6(T - 273.15)\]

At temperatures above 1042.15 K, the rupture time is determined using:

(9.2-109)\[ t_{r} = t_{rt}\]

9.2.9.2. Steady-state CDF model

(9.2-110)\[ t_{rs} = min(t_{r1},t_{r2})\]

(9.2-111)\[ {log(t}_{r1}) = - 32.49 + \frac{57781}{T} - \frac{11800}{T}log(\sigma_{\theta})\]

(9.2-112)\[ {log(t}_{r2}) = - 35.173 + \frac{45858}{T} - \frac{5563}{T}\log\left( \sigma_{\theta} \right)\]

where \(t_{r}\) is the clad rupture time (h), T is the clad Temperature (K), and \(\sigma_{\theta}\) is the clad Hoop Stress (MPa) [9-30].

9.2.9.3. Transient CDF Model

(9.2-113)\[ dx0 = \tanh\left\lbrack 2.0 \times 10^{-2} \times \left( \sigma_{\theta} - 200 \right) \right\rbrack\]

(9.2-114)\[ dx1 = \tanh\left\lbrack \frac{\frac{dT}{dt} - 58}{17} \right\rbrack\]

(9.2-115)\[ dx2 = \left( - 0.5 \times (1 + dx0) \right) \times \left( 0.75 \times (1 + dx1) \right)\]

(9.2-116)\[ ax2 = - 34.8 + dx0 + dx2\]

(9.2-117)\[ bx2 = \frac{12}{1.5 + 0.5 \times dx0}\]

(9.2-118)\[ wx2 = ax2 + bx2 \times \log\left\lbrack \log\frac{\sigma^{*}}{\sigma_{\theta}} \right\rbrack\]

(9.2-119)\[ t_{rt} = e^{wx2} \times e^{\frac{Q}{RT}}\]

where \(\sigma^{*} = 730\) (MPA), Q = 70107 (Cal/mol), R=1.987 (Cal/mol/K), \(\sigma_{\theta}\) is the clad hoop stress (MPa), T is the Temperature (K), \(\frac{dT}{dt}\) is the rate of change of clad temperature (K/s), and \(t_{r}\) is the clad rupture time (s), [Section 9.8.8.2.4].

9.2.9.4. D9 CDF Model

The D9 CDF model determines the rupture time based on the temperature and stress [9‑19]. The D9 CDF model is not applicable during pre-transient characterization and is only calculated during transient calculations. The time to rupture is determined using:

(9.2-120)\[ T_{r} = - 0.28 + 1.18\tanh\left\lbrack 0.5\left( 1 - \ln\left( \frac{dT}{dt} \right) \right) \right\rbrack\]

(9.2-121)\[ d_{0} = \tanh\left\lbrack \frac{1000 - T_{irr}}{200} \right\rbrack\]

(9.2-122)\[ d_{1} = \tanh\left\lbrack \frac{\psi}{2} \right\rbrack\]

(9.2-123)\[ d_{2} = \tanh\left\lbrack\left( \frac{\min(1,\sigma)}{550} \right)^{10} \right\rbrack\]

(9.2-124)\[ d_{3} = 1 - \tanh\left\lbrack \left( \frac{T_{irr}}{583} - 0.438 \right)^{25} \right\rbrack\]

(9.2-125)\[ d_{4} = \tanh\left\lbrack \frac{\psi}{2.5} \right\rbrack\]

(9.2-126)\[ \sigma_{s} = 775 - 387.5\left( 1 - d_{0} \right)\ d_{1} + 125d_{2}d_{3}d_{4}\]

(9.2-127)\[ \ln\left( t_{r} \right) = - 43.6 + 7.312\log\left( \log\left( \frac{\sigma_{s}}{\sigma} \right) \right) - \frac{41399}{T} + T_{r} - 1.73\tanh\lbrack\psi\rbrack\]

where \(\sigma\) is the stress (MPa), T is the temperature (K), \(\frac{dT}{dt}\) is the rate of change of clad temperature (K/s), \(\psi\) is the neutron fluence (#/cm²/1.0E22), \(T_{irr}\) is the temperature of cladding during irradiation (K), and \(t_{r}\) is the clad rupture time (hr).

9.2.9.5. Numerical Solution

It is assumed that at time = 0, the CDF is zero. For each channel and axial node, the CDF is computed using:

(9.2-128)\[ {CDF}^{t} = {CDF}^{t - 1} + \frac{\mathrm{\Delta}t}{t_{r}^{t}(\sigma,T)}\]

where \(\mathrm{\Delta}t\) is the time step (s), \(t_{r}^{t}\) is the time to rupture at a given stress and temperature, \(\sigma\) is the stress (Pa), and T is the temperature (K).

9.2.10. Mechanistic Clad Creep Rupture

A mechanistic-based and semi-empirical clad failure model has been developed for HT9 cladding. The model aims at capturing the cavity dynamics; nucleation, growth, and coalescence behavior; cavity morphological evolution, and its connection with the rupture behavior. The interactions between cavities are modeled similar to a previously-developed mechanistic approach for fission gas bubbles [9‑10], [9‑11]. The cavity growth is modeled using the assumption and equation for the constrained diffusional cavity growth [9‑20], [9‑21]. Furthermore, the growth model is extended to account for the effect of the heterogeneities such as grain boundary carbides on the nucleation and growth behavior. A schematic description of the model is shown in Figure 9.2.3. Three different cavity types are allowed based on their sizes. The selected radius for each type is 0.05, 0.25, and 1.25 µm, respectively, based on experimental observations [9‑20]. Small cavities nucleate at the grain boundaries proportional to the creep rate. The cavity growth under the applied stress occurs via creep and grain boundary diffusion. The growth rate of the cavities is used to compute the coalescence probabilities and the coalescence rate. As a result, the evolution of the cavity density and size is predicted. When the cavity areal fraction reaches 30%, failure is assumed.

The progression of the mechanistic creep failure (MCF) model is quantified using:

(9.2-129)\[ MCF = \frac{A_{cav}}{A_{cr}} \leq 1.0\]

\[A_{cr} = 0.3\pi R_{gb}^{2}\]

\[A_{cav} = \pi\left( R_{c1}^{2}N_{c1} + R_{c2}^{2}N_{c2} + R_{c3}^{2}N_{c3} \right)\]

where \(A_{cav}\) is the cavitated grain boundary area (m²), \(A_{cr}\) is the critical cavitated grain boundary area(m²), \(R_{gb}\) is the radius of the grain boundary, assumed to be 10 microns, \(N_{ci}\) is the number of type-i cavities, and \(R_{ci}\) is the radius of cavity type-i (\(m\)).

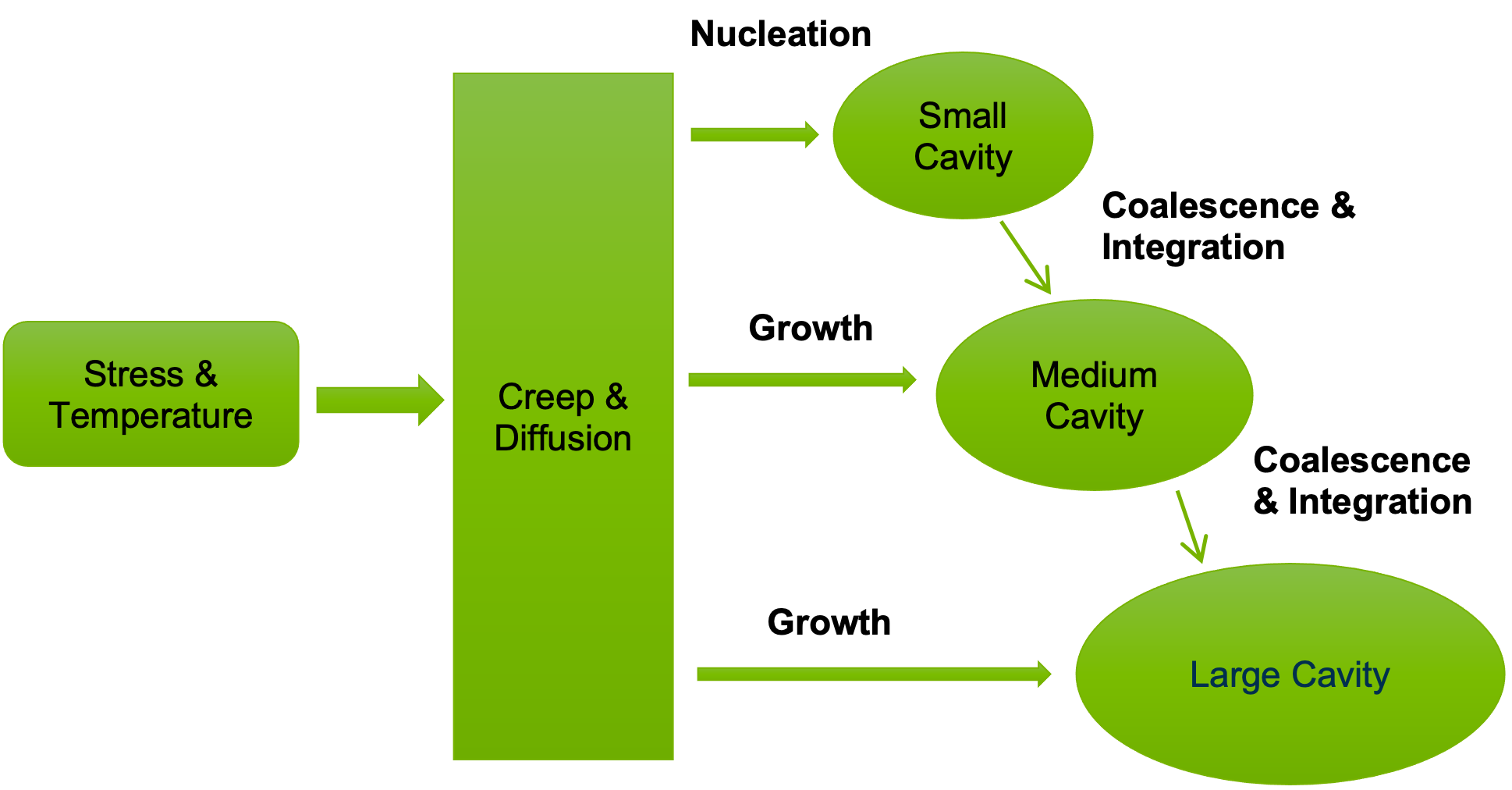
Figure 9.2.3 Schematic description of the mechanistic creep failure model (MCF)

The number density of the different cavity types is determined using:

(9.2-130)\[ \frac{dN_{c1}}{dt} = J_{nucl} + J_{c1} - f_{12}\left( gc_{11} + gc_{12} + gc_{13} \right) - f_{13}\left( gc_{13} + gc_{31} \right)\]

(9.2-131)\[ \frac{dN_{c2}}{dt} = J_{c2} + f_{12}\left( gc_{11} + gc_{12} + gc_{13} \right) - f_{23}\left( gc_{22} + gc_{23} + gc_{32} \right)\]

(9.2-132)\[ \frac{dN_{b3}}{dt} = J_{c3} + f_{13}\left( gc_{13} + gc_{31} \right) + f_{23}\left( gc_{22} + gc_{23} + gc_{32} \right)\]

where \(J_{ci}\) is the cavity surface density rate of change due to stress induced cavity growth (1/s), \(J_{nucl}\) is the nucleation rate of type-1 cavities (1\(/s\)), \({gc}_{ij}\) is the coalescence and integration rate of cavity-i into cavity-j due to growth of cavity-i (1\(/s\)), and \(f_{i,j}\) is the transition probability of cavity-i into cavity-j due to coalescences, \(\frac{V_{cavi}}{V_{cavj}}\), \(V_{cavi}\) and \(V_{cavj}\) are the cavity volume of i and j cavity groups.

The MCF model is a system of ordinary differential equations and is solved using a backwards Euler method. The system of ordinary differential equations is solved independently for every axial node of the fuel pin. Prior to pre-transient irradiation, MFUEL assumes that MCF is zero.

9.2.10.1. Cavity Nucleation

Nucleation rate of cavities (\(J_{nuc}\)) is given as a function of a rate constant (\(K_{nuc}\)), creep rate (\({\dot{\epsilon}}_{c}\)), and the grain boundary area \((A_{gb})\):

(9.2-133)\[ J_{nuc} = K_{nuc}{\dot{\epsilon}}_{c}A_{gb}\]

The nucleation constant depends on the operating stress, temperature, and microstructural heterogeneities. An empirical constant, which is called “G correction factor” has been derived in this work to account for the modeling imperfections associated with the nucleation and growth of the cavities and uncertainties in constitutive models. The nucleation constant is modeled as a function of the G correction factor. G is a tabular function depending on the stress and temperature as described in Section 9.8.6.

(9.2-134)\[ K_{nuc} = 1.0 \times 10^{12}G\]

9.2.10.2. Cavity Growth

Rice’s constrained diffusional cavity growth model [9‑20], [9‑21] is adopted to compute the rate of change of the cavity size. However, the model is extended in several ways. First, continuous nucleation is modeled, allowing the spacing between the cavities and cavity density to change dynamically, in addition to change in the cavity size. Second, multiple sizes of cavity groups are allowed instead of single cavity size. These two improvements are much more consistent with the experimental observations. Finally, in order for the theoretical model to predict the real behavior including the microstructural complexities/heterogeneities, a correction factor, called G, is applied both to nucleation and growth rate. G correction factor is described in Section 9.8.6. The equation for the rate of change of cavity radius is given as follows:

(9.2-135)\[ \frac{dr}{dt} = G\frac{\sigma - (1 - w)\sigma_{0}}{h(\Psi)r^{2}\left\lbrack \frac{q(w)kT}{2\Omega\delta D_{b}} + \frac{q^{'}\sigma}{{\dot{\epsilon}}_{c}\lambda^{2}d} \right\rbrack}\]

\[\sigma_{0} = \frac{2\gamma_{s}sin\Psi}{2}\]

r: Cavity radius (m)

\(\sigma\): Applied stress (Pa)

\(\sigma_{0}\): Sintering stress (Pa)

d: Grain boundary facet =20 μm

λ: Effective cavity pitch (m)

w: 4r²/λ²

Ω: Atomic volume = 1.18E-29 \(m^{3}\)

\(\delta\): Grain boundary thickness (m)

Ψ: Tip angle of the cavities \(\cos\Psi = \frac{\gamma_{b}}{2\gamma_{s}}\)

\[q(w) = - 2\ln(w) - (3 - w)(1 - w)\]

\[h(w) = \frac{1}{sin\Psi}\left\lbrack \frac{1}{1 + cos\Psi} - \frac{cos\Psi}{2} \right\rbrack\]

\(\gamma_{b}\): Grain boundary free energy = 0.85 \(J/m^{2}\)

\(\gamma_{s}\): Surface free energy = 2.1 \(J/m^{2}\)

G: Empirical constant to capture heterogeneity effects described in Section C.3.5

\(D_{b}\): Grain boundary diffusion coefficient, \(\delta D_{b}\) = \(1.1 \times 10^{12}\exp\left( - \frac{1.75 \times 10^{5}}{RT} \right)\) (\(m^{2}\)/s)

R: Gas constant = 8.315 J/mol/K

\[q^{'} = \pi^{2}\left( 1 + \frac{3}{n} \right)^{1/2}\]

n: Power law stress exponent in creep relation = 6.6

9.2.10.3. Cavity Coalescence

The coalescence probabilities are calculated based on the derivations given in Ref. [9‑11], [9‑12]. The coalescence probability of cavity-i and cavity-j due to the growth of cavity-i, where i \(\neq j\), is given as follows:

(9.2-136)\[ P_{ij} = \frac{\Delta r_{i}}{0.5l_{j} - r_{i} - r_{j}}\]

for i = j, the following relation is used:

(9.2-137)\[ P_{ij} = 2\frac{\Delta r_{i}}{l_{j} - r_{i} - r_{j}}\]

\(P_{ij}\): Coalescence probability of cavity-i and cavity-j due to the growth of the cavity-i

\(\Delta r_{i}\): Change in radius of cavity group-i at a given time step (m)

\(l_{j}\): Distance between cavities belonging to group-j (m)

\(r_{i}\): Cavity radius of group-I (m)

\(r_{j}\): Cavity radius of group-j (m)

The resulting integration rate is the multiplication of the probability \({(P}_{ij})\) and smaller cavity number for i and j, N_min(i,j):

(9.2-138)\[ {gc}_{ij} = P_{ij}N_{\min(i,j)}\]

9.2.11. Clad Failure Assessment

Clad failure in metal fuel pins with ferritic/martensitic cladding is primarily thermal creep rupture that is augmented by the clad inner wastage formation. Thermal creep rupture can be assessed using thermal creep strain, CDF or MCF models. For a given SAS channel, when the thermal creep hoop strain reaches 1%, CDF or MCF reaches 1, the code prints a message indicating a clad failure prediction due to corresponding mechanism. While computing the clad stress, the model subtracts the clad wastage assuming the corresponding clad thickness does not bear any load; however, when the clad wastage is excessively high, this approach may not be conservative. As a result, when 50% of the clad thickness turns into clad wastage, clad failure is assumed due to excessive clad wastage. The deterministic approach assumes that all fuel pins corresponding to the SAS channel failed.

These failure assessments cover the majority of the normal operation and transient scenarios. In addition, operation with excessive irradiation creep or void swelling strain (>2%) could lead to irradiation induced embrittlement, fuel assembly distortion, local undercooling and blockages. At current implementation, cladding failure does not activate the fuel failure relocation models.