8.7. Material Properties

All material property data are cast as functions or subroutines to allow for modularization and the ease of making changes. This also allows for the incorporation of different materials data in a straightforward manner. In a number of the correlations used, the units are inconsistent with the SI unit system adopted by SAS4A. The routines that use these correlations carry out appropriate units conversions internally.

8.7.1. Fuel Density

The solid fuel density is assumed to have the functional form

(8.7-1)\[\rho_{\text{f}} = \frac{\rho_{\text{o}}}{1 + C_{1} \left( T - 273 \right) + C_{2} \left( T - 273 \right)^{2}}\]

where

\(\rho_{\text{o}}\) = The theoretical density at 273 K, kg/m³

\(C_{1},C_{2}\) = Input coefficients

\(T\) = Temperature, K

This applies between 273 K and the solidus temperature.

The liquid fuel density is given by

(8.7-2)\[\rho_{\text{l}} = \frac{\rho_{\text{o}}}{1 + C_{3} \left( T - 273 \right)}\]

where

\(C_{3}\) = Input coefficient

This applies to temperatures above the liquidus. For the range between the solidus and liquidus temperatures, a linear interpolation is performed.

These equations are found in the function RHOF. Suggested values of coefficients are from the Nuclear Systems Materials Handbook [8‑17].

\(\rho_{\text{o}} = \text{COEFDS} \left( 1 \right) = 11.05 \times 10^{3}\) kg/m³ (mixed oxide)

\(C_{1} = \text{COEFDS} \left( 2 \right) = 2.04 \times 10^{-5}\) K^-1

\(C_{2} = \text{COEFDS} \left( 3 \right) = 8.70 \times 10^{-9}\) K^-2

\(C_{3} = \text{COEFDL} \left( 2 \right) = 9.30 \times 10^{-5}\) K^-1

8.7.2. Fuel Thermal Expansion Coefficient

The thermal expansion coefficient of the fuel is derived from the coefficients of the fuel density function. This assures consistency between the thermal expansion and the density.

The specific volume (inverse of density) at two temperatures is given by

(8.7-3)\[v_{1} = \frac{1 + C_{1} \left( T_{1} - 273 \right) + C_{2} \left( T_{1} - 273 \right)^{2}}{\rho_{\text{o}}}\]

(8.7-4)\[v_{2} = \frac{1 + C_{1} \left( T_{2} - 273 \right) + C_{2} \left( T_{2} - 273 \right)^{2}}{\rho_{\text{o}}}\]

The change in volume is therefore given by

(8.7-5)\[\begin{split}\Delta v_{1} = v_{2} - v_{1} = \frac{1}{\rho_{\text{o}}} \left\{ \left\lbrack C_{1} + C_{2} \left( T_{2} - 273 \right) \right\rbrack \left( T_{2} - 273 \right) \right. \\ \left. - \left\lbrack C_{1} + C_{2} \left( T_{1} - 273 \right) \right\rbrack\left( T_{1} - 273 \right) \right\}\end{split}\]

Eq. (8.7-5) can be rewritten in terms of the bulk thermal expansion coefficient, \(\beta\).

(8.7-6)\[\Delta v = \frac{1}{\rho_{\text{o}}} \left\{ \beta \left( T_{2} \right) \left( T_{2} - T_{\text{r}} \right) - \beta \left( T_{1} \right) \left( T_{2} - T_{\text{r}} \right) \right\}\]

where

\(\beta \left( T \right) = C_{1} + C_{2} T\)

\(T\) = Temperature, K

\(C_{1},C_{2}\) = Density function coefficients

\(T_{\text{r}}\) = Reference temperature, K

Since the linear expansion coefficient is assumed to be a third of the bulk expansion coefficient, the linear expansion coefficient can be defined from the density coefficients as

(8.7-7)\[\alpha \left( T \right) + {C'}_{1} + {C'}_{2} T\]

where

\(\alpha\) = Linear thermal expansion coefficient

\({C'}_{1} = \frac{C_{1}}{3}\)

\({C'}_{2} = \frac{C_{2}}{3}\)

\(T\) = Temperature, K

This is found in the function ALPHF.

8.7.3. Fuel Modulus of Elasticity

The modulus of elasticity, Young’s Modulus, is determined from the bulk modulus by

(8.7-8)\[E = 3\left( 1 - 2v \right) K\]

where

\(E\) = Modulus of elasticity, Pa

\(K\) = Bulk modulus, Pa

\(v\) = Poisson’s ratio

The bulk modulus is from the NSMH [8‑17] and is given by

(8.7-9)\[K = 1.38 \times 10^{11} \left\lbrack 1 - 0.5 \left( T/2760 \right)^{2} \right\rbrack \left( 1 - 2P \right)\]

where

\(K\) = Bulk moduus, Pa

\(T\) = Temperature, °C

\(P = 1 - \rho_{\text{TD}}\) = Porosity fraction

\(\rho_{\text{TD}}\) = Fraction of theoretical density

Based on the evaluation in MATPRO‑l0 [8‑11], if this calculated modulus of elasticity becomes less than \(7.9 \times 10^{8}\), it is fixed at this value.

These equations are solved in the function EFUELF.

8.7.4. Mixed Oxide Fuel Thermal Conductivity

Four different options exist for the fuel thermal conductivity. These are controlled through the input parameter IRHOK.

IRHOK = 0

The thermal conductivity as a function of temperature is input in table form through the variable arrays XKTAB and XKTEM.

IRHOK = 1

For this option, the conductivity equations [8-3] are given by

(8.7-10)\[ \begin{aligned} k_{1} \left( T \right) = 1.1 + \frac{1 \times 10^{2}}{T \left( 0.4848 - 0.4465f_{\text{D}} \right)} && \text{for } 800 \text{ C} \leq T \leq 2000 \text{ C} \end{aligned}\]

(8.7-11)\[ \begin{aligned} k_{1} \left( T \right) = k_{1} \left( 800 \right) \frac{168.844}{12.044 + \left( 0.196 \right)T} && \text{for } T < 800 \text{ C} \end{aligned}\]

(8.7-12)\[ \begin{aligned} k_{3} \left( T \right) = k_{1} \left( 2000 \right) && \text{for } T > 2000 \text{ C} \end{aligned}\]

where

\(k_{1}\), \(k_{2}\), \(k_{3}\) = Fuel thermal conductivity, W/m-K

\(T\) = Temperature, °C

\(f_{\text{D}}\) = Fuel fraction of theoretical density

IRHOK = 2

This form of the conductivity [8‑22] is given by

(8.7-13)\[ \begin{aligned} k_{1} \left( T \right) = \left\lbrack \left( C_{1} - f_{\text{D}} \right) f_{\text{D}} - 1 \right\rbrack\left\lbrack \frac{1}{\left( C_{1} + C_{3} T \right)} + C_{4} T^{3} \right\rbrack && \text{for } 0.75 \leq f_{\text{D}} \leq 0.95 \end{aligned}\]

(8.7-14)\[ \begin{aligned} k_{2} \left( T \right) = \left( 3f_{\text{D}} - 1 \right) \left\lbrack \frac{1}{\left( C_{5} + C_{6} T \right)} + C_{7} T^{3} \right\rbrack && \text{for } f_{\text{D}} > 0.95 \end{aligned}\]

where

\(C_{1}\), \(C_{2}\), \(C_{3}\), \(C_{4}\), \(C_{5}\), \(C_{6}\), \(C_{7}\) = Input variables

\(k_{\text{l}}\), \(k_{2}\) = Fuel conductivity W/m-K

\(T\) = Temperature, K

If \(T\) is greater than the melting temperature, it is set to the melting temperature.

Suggested values:

\(C_{1} = \text{COEFK} \left( 1 \right) = 2.1\)

\(C_{2} = \text{COEFK} \left( 2 \right) = 2.88 \times 10^{-3}\)

\(C_{3} = \text{COEFK} \left( 3 \right) = 2.52 \times 10^{-5}\)

\(C_{4} = \text{COEFK} \left( 4 \right) = 5.83 \times 10^{-10}\)

\(C_{5} = \text{COEFK} \left( 5 \right) = 5.75 \times 10^{-2}\)

\(C_{6} = \text{COEFK} \left( 6 \right) = 5.03 \times 10^{-4}\)

\(C_{7} = \text{COEFK} \left( 7 \right) = 2.91 \times 10^{-11}\)

IRHOK = 3

This conductivity form is [8‑32]

(8.7-15)\[ k_{1} \left( T \right) = \frac{4.005 \times 10^{3}}{\left( T - 273 \right) + 402.4} + 0.6416 \times 10^{-10} T^{3}\]

where

\(T\) = Temperature, K

\(k\) = Conductivity in W/m-K

This is the correlation for UO₂ and is converted to mixed oxide by subtracting 0.2.

(8.7-16)\[ k_{2} \left( T \right) = k_{1} \left( T \right) - 0.2\]

The porosity correction term was derived for use in the COMETHE‑IIIJ [8‑33] code and is given by

(8.7-17)\[ f_{\text{p}} = 1 - 1.029 \varepsilon - 3.2 \varepsilon^{2} - 40.1 \varepsilon^{3} + 158 \varepsilon^{4}\]

where

\(f_{\text{p}}\) = Porosity multiplier

\(\varepsilon = 1 - \rho_{\text{f}}\) = Fractional porosity

\(\rho_{\text{f}}\) = Fractional fuel density = actual density/theoretical density

The conductivity is therefore given by

(8.7-18)\[ k \left( T \right) = f_{\text{p}} \times k_{2} \left( T \right)\]

Two different routines contain the above correlations, FK and KFUEL. The function FK returns a single value of the conductivity for a single invocation and is used in the pre‑transient. The subroutine KFUEL returns the conductivity values for each radial node in the current axial segment. It is used in the transient calculational procedure.

8.7.5. Mixed Oxide Fuel Fracture Strength

The fracture strength for mixed‑oxide fuel is from the NSMH [8-17] and is for unirradiated fuel.

(8.7-19)\[ \sigma_{\text{f}} = 2.74 \times 10^{7} + 5.9 \times 10^{4} T\]

This is coded in the function SIGFRA.

8.7.6. Mixed Oxide Fuel Creep Rate

The fuel creep rate function is from the NSMH [8‑17] and is used in the subroutine FSWELL. It represents diffusional flow, dislocation creep, fission‑enhanced thermal creep, and fission‑induced creep.

(8.7-20)\[\begin{split}{\dot{\varepsilon}}_{\text{total}} = \frac{A}{d^{2}} \left\lbrack 1 + 2.11 \left( 97 - \text{TD} \right) \right\rbrack\sigma \exp\left( - \frac{Q_{1}}{\text{RT}} \right) \\ + B \left\lbrack 1 + 0.22 \left( 97 - \text{TD} \right) \right\rbrack \sigma^{4.4} \exp\left( - \frac{Q_{2}}{\text{RT}} \right) \\ + C \sigma \dot{F} \exp\left( - \frac{Q_{3}}{\text{RT}} \right) + D \sigma \dot{F}\end{split}\]

where

\({\dot{\varepsilon}}_{\text{total}}\) = Creep rate, s^-1

\(A = 8.97222 \times 10^{5}\)

\(d\) = Grain size, \(\mu \text{m}\)

\(\text{TD}\) = Fuel percent of theoretical density

\(\sigma\) = Stress, MPa

\(Q_{1} = 3.87173 \times 10^{5}\)

\(R\) = Gas constant = 8.3169 J/mole-K

\(T\) = Temperature, K

\(\beta = 9.0 \times 10^{2}\)

\(Q_{2} = 5.72598 \times 10^{5}\)

\(C = 7.8889 \times 10^{-21}\)

\(F\) = Fission rate, fissions/cm³-s

\(Q_{3} = 5.7343 \times 10^{4}\)

\(D = 1.5 \times 10^{-24}\)

This is used to calculate the fuel creep for fission‑gas bubble expansion or contraction in the routine FSWELL.

8.7.7. Cladding Thermal Expansion Coefficient

The mean thermal expansion coefficient of the cladding is taken from the Nuclear Systems Materials Handbook [8‑17]. It has the form

(8.7-21)\[ \alpha_{\text{m}} = C_{1} \left( C_{2} \right)^{\left( C_{3} \right)^{T}}\]

where

\(\alpha_{\text{m}}\) = Mean thermal expansion coefficient, °F^-1

\(C_{1}\), \(C_{2}\), \(C_{3}\) = Calibration constants

\(T\) = Temperature, °F

The values for the calibration are given below:

\(C_{1} = 11.397\)

\(C_{2} = 0.71828\)

\(C_{3} = 0.99890\)

This is calculated in the function ALPHC.

8.7.8. Cladding Modulus of Elasticity

The cladding modulus of elasticity is taken from the NSHM [8-17] and is given by

(8.7-22)\[ E_{\text{c}} = 2.833669 \times 10^{1} - 2.882211 \times 10^{- 3} T - 3.687849 \times 10^{-6} T^{2} + 7.709188 \times 10^{-10} T^{3}\]

where

\(E\) = Modulus of elasticity, Mpsi

\(T\) = Temperature, °F

This is then converted to Pa by multiplying by \(6.894757 \times 10^{9}\). This correlation is coded in the function ECLADF.

8.7.9. Cladding Ultimate Tensile Strength

The ultimate tensile strength of unirradiated, 20% cold‑worked, 316 SS is taken from the NSMH [8‑17].

(8.7-23)\[ \sigma_{\text{u}} = C_{0} + C_{1} T + C_{2}T^{2} + C_{3}T^{3} + C_{4} T^{4} + C_{5} T^{5} + C_{6} T^{6} + C_{7} T^{7}\]

where

\(\sigma_{\text{u}}\) = Ultimate tensile strength, ksi

\(T\) = Temperature, F

\(C_{0} = 1.220241 \times 10^{2}\)

\(C_{1} = -1.015998 \times 10^{-1}\)

\(C_{2} = 8.336636 \times 10^{-4}\)

\(C_{3} = -3.365737 \times 10^{-6}\)

\(C_{4} = 6.227377 \times 10^{-9}\)

\(C_{5} = -5.736229 \times 10^{-12}\)

\(C_{6} = 2.542064 \times 10^{-15}\)

\(C_{7} = -4.321098 \times 10^{-19}\)

This is then converted to SI units by multiplying by \(6.894757 \times 10^{6}\).

This correlation is good for temperatures below 1200 K only. For temperatures above 1200 K, the curve is assumed to go to zero at the cladding solidus according to the following equation.

(8.7-24)\[ \sigma_{\text{u}} = \sigma_{\text{u}} \left( 1200K \right) \left\{ 1 - \left\lbrack \frac{T - 1200}{T_{\text{mc}} - 1200} \right\rbrack^{2} \right\}\]

where

\(\sigma_{\text{u}} \left( 1200 K \right) = 1.122 \times 10^{8}\) Pa

\(T\) = Temperature, K

\(T_{\text{mc}}\) = Cladding solidus temperature, K

Care should be exercised when using the function UTS since it is for unirradiated cladding and may be inconsistent with the option used for the cladding flow stress.

8.7.10. Cladding Flow Stress

There exist four different options available to control the cladding flow stress calculation in the function YLDCF. These are controlled through the input parameter IYLD.

IYLD = 0

The value is calculated from the correlation in the NSMH [8‑17] for unirradiated, 20% cold‑worked, 316 SS. For temperatures below 1200 K the following form is used. It should be noted that this correlation is for the strain rate of the tensile tests and may not be appropriate in many accident cases with high strain rates.

(8.7-25)\[ \sigma_{\text{y}} = C_{0} + C_{1} T + C_{2} T^{2} + C_{3} T^{3} + C_{4} T^{4} + C_{5} T^{5} + C_{6} T^{6} + C_{7} T^{7} + C_{8} T^{8} + C_{9} T^{9} + C_{10} T^{10}\]

where

\(\sigma_{\text{y}}\) = Clad flow stress, ksi

\(T\) = Temperature, °F

\(C_{0} = 9.611825 \times 10^{1}\)

\(C_{1} = -1.262505 \times 10^{-1}\)

\(C_{2} = 1.510991 \times 10^{-3}\)

\(C_{3} = -1.021806 \times 10^{-5}\)

\(C_{4} = 3.796623 \times 10^{-8}\)

\(C_{5} = -8.438888 \times 10^{-11}\)

\(C_{6} = 1.163911 \times 10^{-13}\)

\(C_{7} = -9.993892 \times 10^{-17}\)

\(C_{8} = 5.177194 \times 10^{-20}\)

\(C_{9} = -1.477323 \times 10^{-23}\)

\(C_{10} = 1.780710 \times 10^{-27}\)

The value is then converted to Pa by multiplying by \(6.894757 \times 10^{6}\).

For temperatures above 1200 K, a form like Eq. (8.7-24) is used for the extrapolation to the melting temperature.

(8.7-26)\[ \sigma_{\text{y}} = \sigma_{\text{y}} \left( 1200 \right) \left\{ 1 - \left\lbrack \frac{T - 1200}{T_{\text{mc}} - 1200} \right\rbrack^{2} \right\}\]

where

\(\sigma_{\text{y}} \left( 1200 \right) = 7.375 \times 10^{7}\) Pa

\(T\) = Temperature, K

\(T_{\text{mc}}\) = Clad solidus temperature, K

IYLD = 1,2

For these values of IYLD, a flow stress model developed by DiMelfi and Kramer [8‑34] is used. If IYLD = 1, the model is temperature, strain, strain rate, and burnup dependent. If IYLD = 2, a high strain rate approximation is used, removing the strain rate dependence.

The flow stress, \(\sigma\), is defined by

(8.7-27)\[ \sigma = \sigma_{\text{s}} - \left( \sigma_{\text{s}} - \sigma_{1} \right) \exp\left( - \frac{\hat{\varepsilon}}{\varepsilon_{\text{c}}} \right)\]

where

\(\sigma_{1}\) = Yield stress of fully annealed, unirradiated material

\(\sigma_{\text{S}}\) = Saturation flow stress approached as increases

\(\hat{\varepsilon}\) = Hardness parameter

\(\varepsilon_{\text{c}}\) = Material parameter

the hardness parameter \(\hat{\varepsilon}\) has two components; \(\varepsilon_{\text{p}}\), the accumulated equivalent plastic strain, and \({\hat{\varepsilon}}_{\phi}\) the hardness due to irradiation, which is determined from

(8.7-28)\[ {\hat{\varepsilon}}_{\phi} = - \varepsilon_{\text{c}} \ln\left( 1 - \left\{ 1 - \exp\left\lbrack - B \left( \phi t - \phi_{\text{o}} t_{\text{o}} \right) \right\rbrack \right\}^{1/2} \right)\]

where

\(B = 3.5 \times 10^{-27}\), m²/n

\(\phi_{\text{o}} t_{\text{o}} = 4.5 \times 10^{25}\), n/m²

\(\phi t\) = Neutron fluence, n/m²

and

(8.7-29)\[ \dot{\varepsilon} = \varepsilon_{\text{p}} + {\hat{\varepsilon}}_{\phi} + \varepsilon_{\text{cw}}\]

where

\(\varepsilon_{\text{cw}}\) = As-fabricated cold‑work strain

The relationship between \(\sigma_{\text{s}}\), \(\sigma_{1}\), and \(\varepsilon_{\text{c}}\) is given by

(8.7-30)\[ \left\lbrack \frac{\sigma_{\text{s}}}{G} - \frac{\sigma_{1}}{G} \right\rbrack \frac{1}{\varepsilon_{\text{c}}} = \frac{\theta_{1}}{G}\]

where

\(\theta_{1}/G = 3.66 \times 10^{-2}\)

\(G = 92.0 - 4.02 \times 10^{-2}\) T, GPa

This relationship is equivalent to assuming that the initial work‑hardening rate \(\theta_{1}\), for annealed material \(\left( \hat{\varepsilon} = 0 \right)\) is constant.

The functions \(\sigma_{\text{s}}\) and \(\sigma_{1}\) are chosen to be of the form

(8.7-31)\[ \frac{\sigma_{\text{s}}}{G} = \frac{\sigma_{\text{SO}}}{G} \left\{ 1 - \exp\left\lbrack - \left( \frac{\dot{\varepsilon}_{\text{p}}}{\dot{\varepsilon}_{\text{OS}}} \right)^{nk} \right\rbrack \right\}^{1/k}\]

(8.7-32)\[ \frac{\sigma_{1}}{G} = \frac{\sigma_{10}}{G} \left\{ 1 - \exp\left\lbrack - \left( \frac{\dot{\varepsilon}_{\text{p}}}{\dot{\varepsilon}_{01}} \right)^{nk} \right\rbrack \right\}^{1/k}\]

where

\({\hat{\varepsilon}}_{\text{p}}\) = Equivalent plastic strain rate

n = Constant = 1/5.35

k = Constant = 2.0

The functions \(\sigma_{\text{SO}}\), \(\sigma_{10}\), \({\dot{\varepsilon}}_{\text{OS}}\), \({\dot{\varepsilon}}_{01}\) are all temperature dependent. The constant \(k\) is a nonphysical parameter that governs the sharpness of the transition between strain‑rate‑dependent and strain‑rate‑independent behavior.

If IYLD = 2, then the above relationships for \(\sigma_{\text{s}}\) and \(\sigma_{1}\) are assumed to have the form

(8.7-33)\[ \frac{\sigma_{\text{s}}}{G} = \frac{\sigma_{\text{SO}}}{G}\]

and

(8.7-34)\[ \frac{\sigma_{1}}{G} = \frac{\sigma_{10}}{G}\]

In both cases, IYLD = 1 or IYLD = 2, the following functions are used

(8.7-35)\[ \frac{\sigma_{\text{SO}}}{G} = 2.06 \times 10^{-3} + \frac{7.12 \times 10^{-1}}{T}\]

(8.7-36)\[ \frac{\sigma_{10}}{G} = 2.00 \times 10^{-2} - 9.12 \times 10^{-6} T\]

The functions \({\hat{\varepsilon}}_{\text{OS}}\) and \({\hat{\varepsilon}}_{01}\) are strong functions of temperature and are related to the dominant creep mechanism. This is assumed to be thermally activated, so Arrhenius relationships are used.

(8.7-37)\[ {\dot{\varepsilon}}_{\text{OS}} = {\dot{\varepsilon}}_{\text{OOS}} \exp\left( - \frac{Q}{RT} \right)\]

(8.7-38)\[ {\dot{\varepsilon}}_{01} = {\dot{\varepsilon}}_{001} \exp\left( - \frac{Q}{RT} \right)\]

where

\(Q/R\) = 38,533, K

\({\dot{\varepsilon}}_{\text{OOS}} = 1.062 \times 10^{14}\), s^-1

\({\dot{\varepsilon}}_{001} = 3.794 \times 10^{12}\), s^-1

Given the above constants and relationships, it is then possible to calculate the flow stress of the cladding.

IYLD = 3

With this selection, the input flow stress table YLDTAB with its corresponding temperature table YLDTEM are searched to find the flow stress as a function of temperature. One table exists for each cladding type.

8.7.11. Thermal Conductivity of Helium

The thermal conductivity of the helium in the fuel pin free volume is temperature dependent and has been fit to the following equation [8‑35].

(8.7-39)\[ K = 1.43 \times 10^{-1} + 3.17 \times 10^{-4} \left( T - 273 \right) - 2.24 \times 10^{-8} \left( T - 273 \right)^{2}\]

where

\(K\) = Thermal conductivity, W m^-1 K^-1

\(T\) = Gas temperature, K

This is used in the function routine HGAP.

8.7.12. Thermal Conductivity of Fission Gas

All fission gas is assumed to be xenon. A functional form of the xenon conductivity [8‑35] is used in the function routine HGAP.

(8.7-40)\[ K = 5.15 \times 10^{-3} + 1.69 \times 10^{-5} \left( T - 273 \right) - 3.50 \times 10^{-9} \left( T - 273 \right)^{2}\]

where

\(K\) = Thermal conductivity, W m^-1 K^-1

\(T\) = Gas temperature, K

8.7.13. Fuel Hardness

In DEFORM‑4 it is assumed that conditions could arise where either the fuel or cladding could be the softer material when considering fuel‑cladding contact in the determination of the gap conductance. The following equation is therefore used to determine the oxide fuel hardness [8‑31].

(8.7-41)\[ H = 6.009 \times 10^{9} \exp\left( - \frac{T}{641} \right)\]

where

\(H\) = Meyer hardness, Pa

\(T\) = Temperature, K

8.7.14. Cladding Hardness

The cladding hardness is calculated from the following equation [8‑21] when comparing with the fuel hardness. The softer of the fuel or cladding is used in the solid‑to‑solid gap conductance considerations.

(8.7-42)\[ \begin{aligned} H = 5.961 \times 10^{9} T^{0.206}~, && T < 893.92 \text{ K} \end{aligned}\]

(8.7-43)\[ \begin{aligned} H = 2.75 \times 10^{22} T^{6.53}~, && T > 893.92 \text{ K} \end{aligned}\]

where

\(H\) = Meyer hardness, Pa

\(T\) = Temperature, K

8.7.15. Cladding Fast Creep

Kramer and DiMelfi [8‑34] have shown that the following equation is suitable for plastic strain of cladding at high temperatures.

(8.7-44)\[ \dot{\varepsilon} = \frac{{\dot{\varepsilon}}_{\text{OOS}}}{\sigma_{\text{SO}}^{n}} \sigma^{n} \exp\left( - \frac{Q_{\text{c}}}{T} \right)\]

where

\(\dot{\varepsilon}\) = Plastic strain rate, s^-1

\(\sigma\) = Equivalent stress in the cladding, Pa

\(T\) = Temperature, K

\({\dot{\varepsilon}}_{\text{OOS}} = 1.062 \times 10^{14}\), s^-1

\(\sigma_{\text{so}}\) = Material constant defined in Eq. (8.7-35)

\(n\) = Stress exponent = 5.35

\(Q_{\text{c}}\) = Creep activation constant = 38,533 K

This allows for plastic deformation of the cladding below the flow stress.

8.7.16. Material Properties of Metal Alloy Fuel

Material properties for the metal fuels under consideration for the Integral Fast Reactor concept are currently under investigation in order to prepare a set of recommended values for use by the safety community. Unlike the oxide fuel which has been under study for a number of years, the metal fuel data is fairly sparse and limited to specific fuel types. Therefore, the correlations given below are to be considered preliminary in nature, but they should provide results that are consistent with future results. These have been coded into DEFORM in a manner that makes future modifications a simple replacement task.

Several thermal properties are also used by DEFORM and these have been addressed in Chapter 10 of this document. Most of the properties given below are obtained from a survey of data carried out for the modification of the FPIN code to analyze metal fuels [8-36].

8.7.16.1. Modulus of Elasticity

Although the modulus of elasticity varies with temperature, composition, and phase, a single average value has been used.

(8.7-45)\[ E_{\text{f}} = 1.4 \times 10^{12}\]

where

\(E_{\text{f}}\) = Modulus of elasticity, Pa

8.7.16.2. Poisson’s Ratio

Poisson’s ratio is an input parameter to the SAS4A code. For both the ternary and fission alloy fuels the currently recommended value is 0.23.

8.7.16.3. Fracture Strength

Unlike the oxide fuels, the metal fuel does not exhibit a fracture phenomenon. While there does appear to be a separation between the phases that result in the ternary fuels, there is no radial cracking. This appears to be the result of the softness of the metal matrix and the inherent structural differences that exist between ceramics and metals. When metal fuel has been specified, the function SIGFRA returns a large value for the fracture strength to avoid cracking during the mechanical calculations.

8.7.16.4. Fuel Creep Rate

One of the more important correlations used by DEFORM is the creep rate of the fuel because of its influence on the rate of fuel swelling through the process of fission gas bubble volume change. For the metal fuels the creep rate, determined in a study performed by John Kramer [8-37], has been employed for both types of metal fuel currently considered in DEFORM.

For uranium phases existing below 973 K, the rate is dependent on two stress related terms.

(8.7-46)\[ R_{\text{c}} = \left( 0.5 \times 10^{4} \sigma + 6.0 \sigma^{4.5} \right) \exp\left( - \frac{26168}{T} \right)\]

where

\(R_{\text{c}}\) = Fuel creep rate, s^-1

\(\Sigma\) = Stress, MPa

T = Temperature, K

For the high temperature gamma uranium phase, the rate is give by a single stress dependent function.

(8.7-47)\[ R_{\text{c}} = 8.0 \times 10^{-2} \sigma^{3} \exp\left( - \frac{14353}{T} \right)\]

The time constant for bubble expansion is the inverse of the calculated creep rate. These functions are coded into the subroutine FSWELL.

8.7.17. 15-15Ti Cladding Properties

8.7.17.1. Thermal Creep

Given the cladding equivalent stress and clad mid-wall temperature at each axial location, the thermal creep correlation computes the thermal creep strain rate at each time step during normal operation as well as transients. The thermal creep equation derived in [8.39] for 15-15Ti cladding has been adopted as is. The form of the equation is given as follows:

(8.7-48)\[{\dot{\epsilon}}_{th,\ Eq} = \left\lbrack sinh(\beta\sigma_{\text{Eq}}) \right\rbrack^{n}e^{- \frac{E}{\text{RT}}}\]

\[E = E_{1} + E_{2}T + E_{3}T^{2}\]

Where \({\dot{\epsilon}}_{th,Eq}\) is the thermal creep strain rate (1/s), \(\sigma_{\text{Eq}}\) is the equivalent stress (MPa), and \(T\) is the clad mid-wall temperature (K). \(R\) is the gas constant, 8.3144621 J/mol/K, and \(E\) is the activation energy (J/mol). \(\beta\), \(n\), and \(E_{1}\),\(\ E_{2}\), and \(E_{3}\) are the fitting parameters, which are given in Table 8.7.1 below.

Table 8.7.1 Fitting parameters for the 15-15Ti Thermal Creep Model

Fitting Parameter	Value
\(\beta\) (1/MPa)	1.4994E-2
\(E_{1}\) (J/mol)	-6.591E+5
\(E_{2}\) (J/mol)	1.8211E+3
\(E_{3}\) (J/mol)	-1.0513
\(n\)	2.3319

8.7.17.2. Irradiation Creep

Given the cladding hoop stress, clad mid-wall temperature, and clad dose rate, which is a function of clad fast neutron flux, at each axial location, the irradiation creep correlation computes the irradiation creep strain rate at each time step. The irradiation creep equation derived in [8.40] for 15-15Ti cladding has been adopted as is. The form of the equation is given as follows:

(8.7-49)\[{\dot{\epsilon}}_{ir,\ \theta} = 0.75 \times A \times \sigma_{\theta} \times {\dot{\varphi}}_{d}\]

Where \({\dot{\epsilon}}_{ir,\ \theta}\) is the irradiation creep strain rate (1/s), \(\sigma_{\theta}\) is the clad hoop stress (MPa), and \({\dot{\varphi}}_{d}\) is the clad dose rate (dpa/s). The cladding dose rate is computed by multiplying the fast neutron flux with the dose conversion factor, CDOSECONV. The fast neutron flux is computed by multiplying FLTPOW with the linear heat rate. \(A\) is the fitting parameter given as a function of clad mid-wall temperature, which is shown in Figure 8.7.1. Below 673 K and above 898 K, the value of \(A\) is set to its value at 673 K and 898 K, respectively.

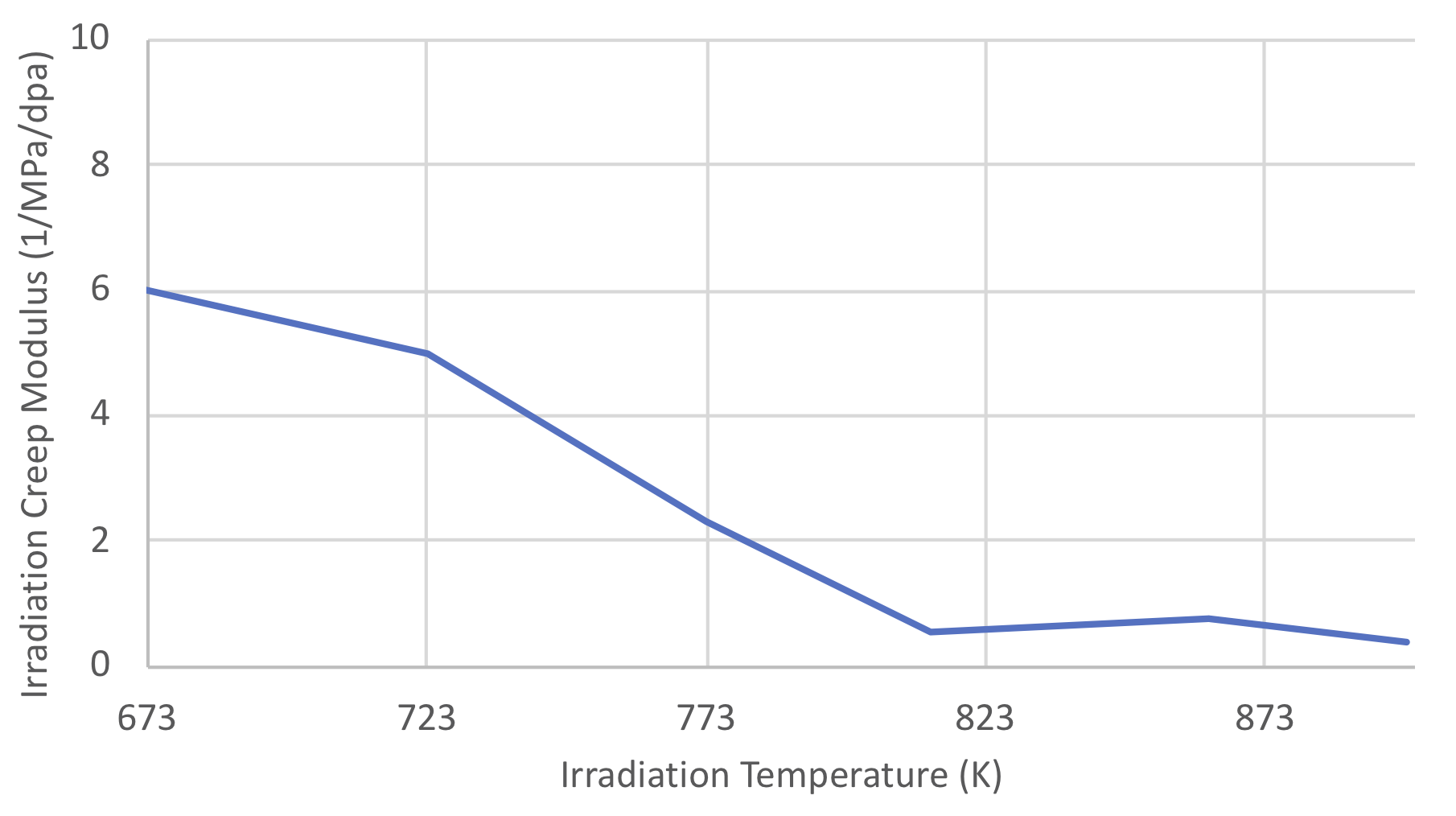
Figure 8.7.1 Irradiation Creep Modulus for 15-15Ti Cladding

8.7.17.3. Void Swelling

Void swelling rate of cladding is modeled as a function of cladding dose and cladding dose rate, which is given as a function of fast neutron flux and temperature. The cladding dose rate is computed by multiplying the fast neutron flux with the dose conversion factor, CDOSECONV. The fast neutron flux is computed by multiplying FLTPOW with the linear heat rate. The void swelling plots given in Figure 8.7.2 [8.40] as a function of cladding dose and clad temperature are used to derive linear piecewise continuous functions to predict the void swelling rate at a given time step.

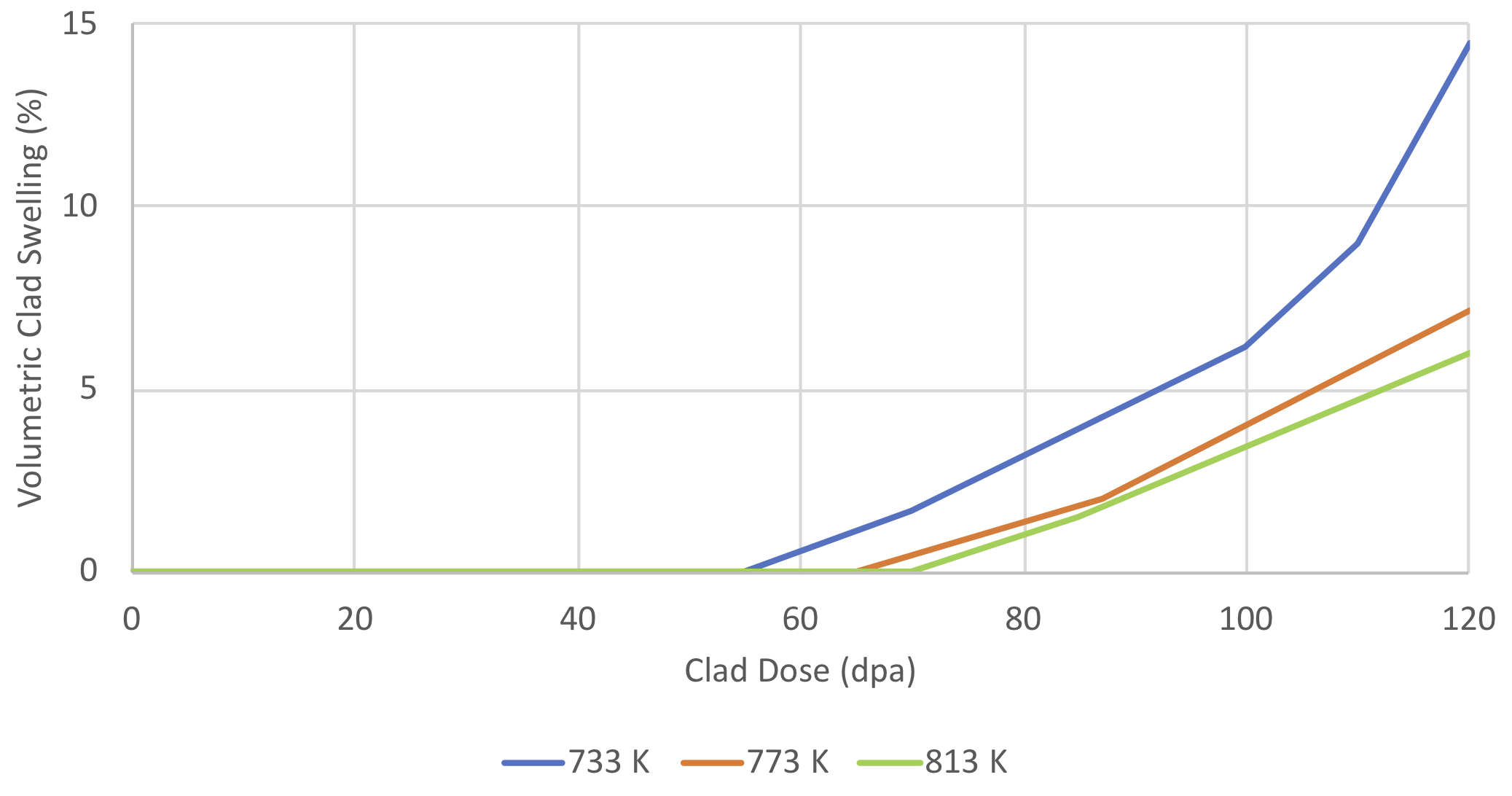
Figure 8.7.2 Experimental Data for volumetric clad swelling as a function of dose at 733 K, 773 K and 813 K for 15-15Ti cladding

8.7.17.4. Transient Creep Rupture

The creep rupture margin of the cladding is computed using the CDF/life fraction model and is a function of hoop stress, mid-wall temperature and dose of the cladding. CDF at any time, \(t_{0}\), during the transient is described by the following relation:

(8.7-50)\[\text{CDF}\left( t_{0} \right) = \int_{0}^{t_{0}}\frac{\text{dt}}{t_{r}(\sigma_{\text{eq}},T,\varphi_{d})}\]

where, \(t_{r}\) is the time to rupture (s), \(\sigma_{\text{eq}}\) is the equivalent stress (MPa), \(T\) is the temperature (K), and \(\varphi_{d}\) is the dose (dpa).

Time to rupture correlations given in [8.39] for the unirradiated 15-15Ti have been extended in order to account for the neutron irradiation induced damage and adopted in this model. The following form is used:

(8.7-51)\[\begin{split}P = \begin{cases}\left\lbrack \frac{A_{1}}{A_{3}}\left( \log\sigma_{\text{eq}} - A_{2} \right) + 1 \right\rbrack\left\lbrack 1 + A_{3} - e^{A_{4}\left( \log\sigma_{\text{eq}} - A_{2} \right)} \right\rbrack & T < 1023.15 \\ B_{1}\log\sigma_{\text{eq}} + B_{2} & T \geq 1023.15 \end{cases}\end{split}\]

\[t_{r} = i_{f} \times 10^{\left( P\frac{1000}{T} - 17.6 \right)} \times 3600\]

where, \(P\) is the Larson-Miller parameter and \(A_{1}\), \(A_{2}\), \(A_{3}\), \(A_{4}\), \(B_{1}\), and \(B_{2}\) are the fitting parameters given in Table 8.7.2.

Table 8.7.2 Fitting parameters for 15-15Ti Time to rupture correlation

Fitting Parameter	Value
\(A_{1}\)	-0.78
\(A_{2}\)	2.3054
\(A_{3}\)	19.512
\(A_{4}\)	5.196
\(B_{1}\)	-6.1175
\(B_{2}\)	31.7882

The modeling of the irradiation induced embrittlement of 15-15Ti was approximated using clad void swelling data and the interrelation between void swelling and clad embrittlement for similar stainless steels such as SS316 and D9 using the creep rupture data given in Refs. [8.41], [8.42], and [8.43]. The \(\ i_{f}\) correction factor is modeled as a function of 15-15-Ti cladding dose as given in Figure 8.7.3. The cladding dose rate is computed by multiplying the fast neutron flux with the dose conversion factor, CDOSECONV. The fast neutron flux is computed by multiplying FLTPOW with the linear heat rate. At high doses where void swelling takes off exceeds 5% and embrittles cladding, the irradiation factor is assumed to be 0.01 consistent with the findings for SS316 cladding. This value is also used for cladding doses that are beyond 120 dpa.

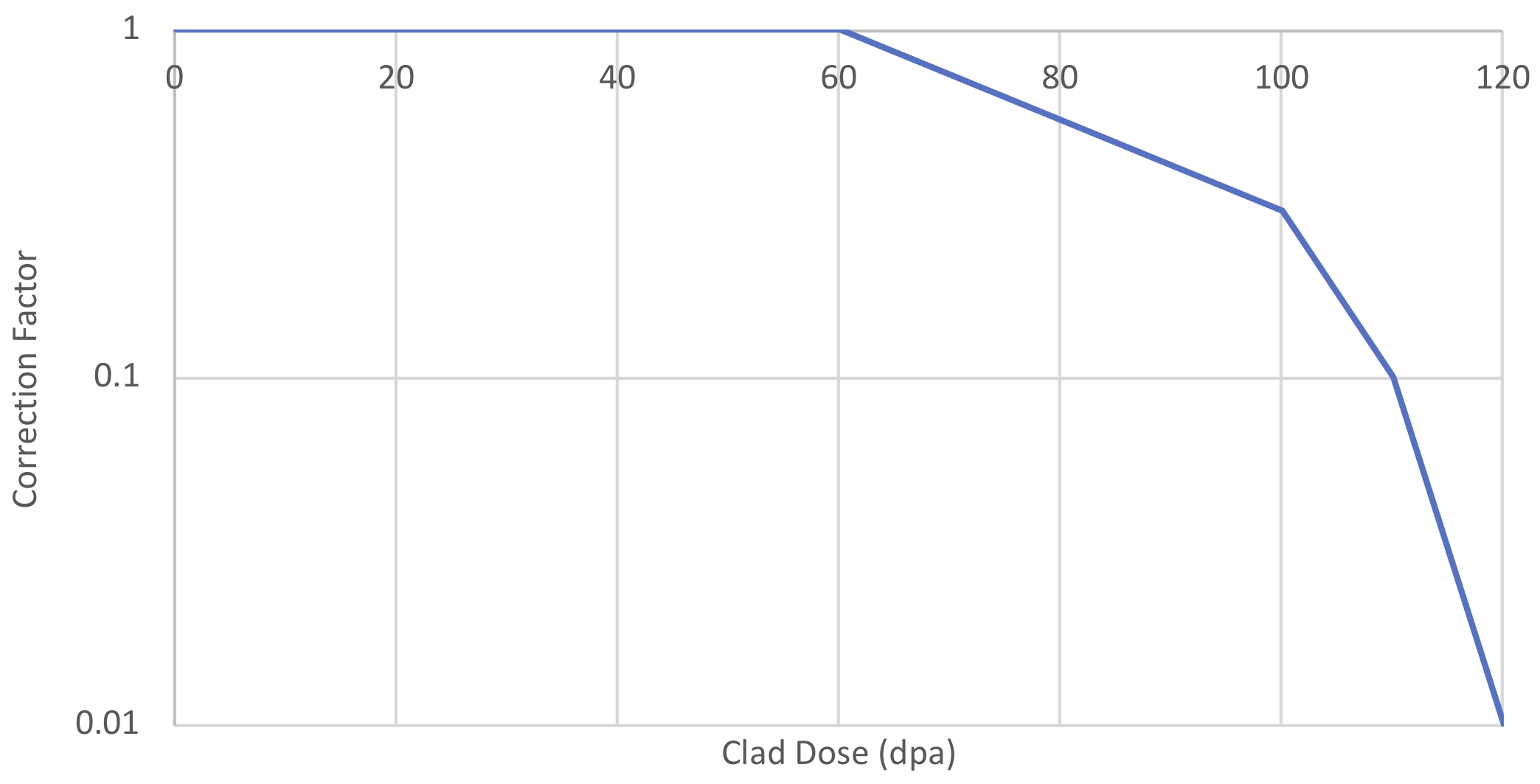
Figure 8.7.3 Approximate irradiation correction factor for 15-15Ti time to rupture as a function of cladding dose

In order to model the stochastic nature of clad failure, a normal probability density function (PDF) has been adopted as a function of the logarithm of the CDF.

(8.7-52)\[\mathrm{\text{PDF}} = \frac{1}{\sqrt{2\pi\sigma^{2}}}\exp\left\lbrack - \frac{\left( \log\mathrm{\text{CDF}} - \mu \right)^{2}}{2\sigma^{2}} \right\rbrack\]

where \(\sigma\) is the standard deviation and \(\mu\) is the mean in units of the logarithm of CDF.

The integral of the PDF given by the equation above is interpreted as the fraction of the fuel pins that are failed. PDF and integral of PDF for \(\sigma = 1\) and \(\mu = 0\) are plotted in Figure 8.7.4. The model currently ignores potential pin-to-pin failure propagation due to fission gas and fuel ejection to the channel, clad ballooning, and blockages.

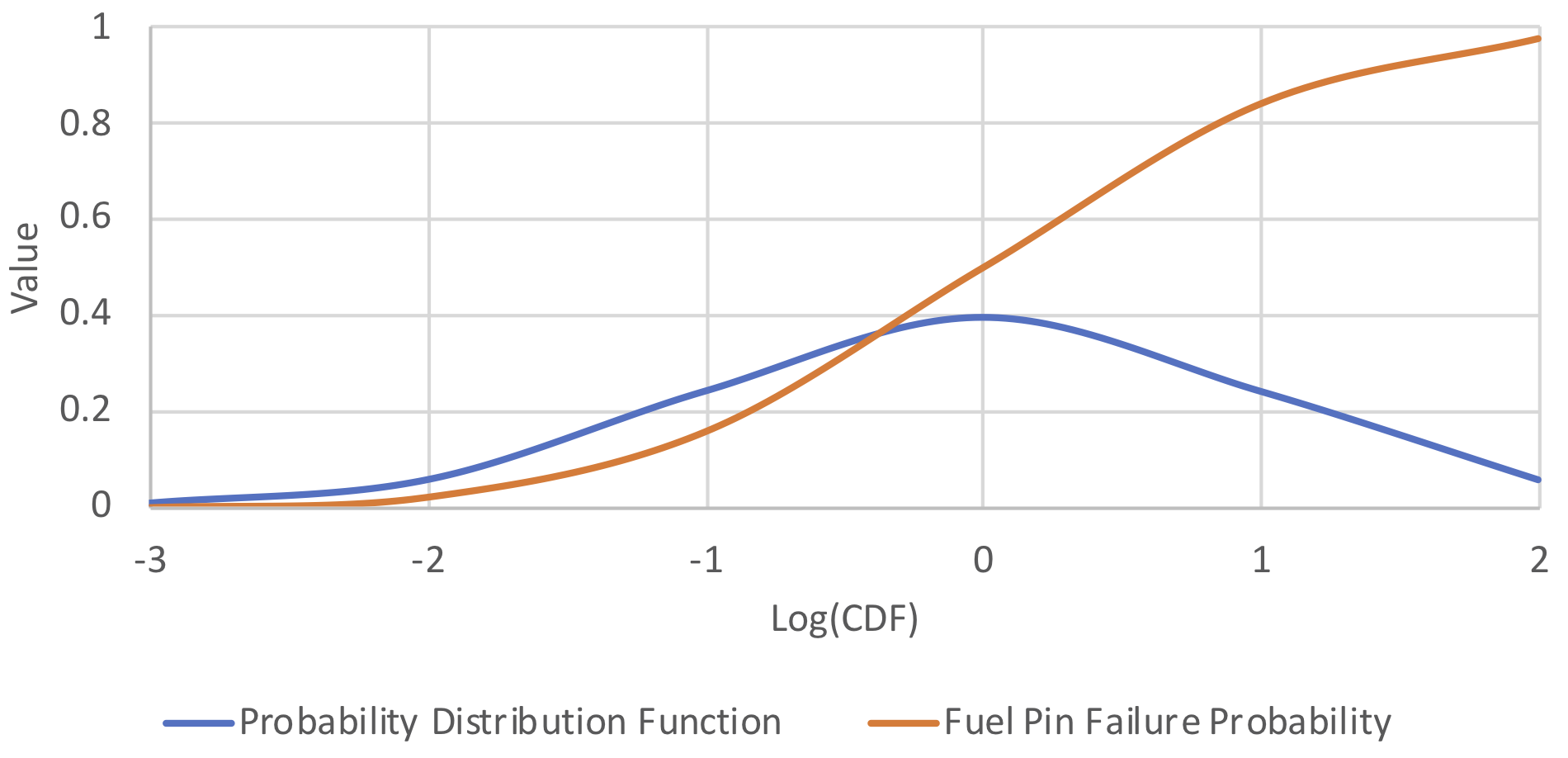
Figure 8.7.4 An example PDF and integral of PDF for \(\sigma=1\) and \(\mu=0\)

8.7.17.5. Cladding Outer Corrosion

Chemical interactions between stainless steel clad and lead coolant is a critical issue of LFR designs. The highly complex nature of the problem and unavailability of corrosion data led to the decision to keep this model simple and mostly dependent on user input. The user is allowed to define the thickness of the cladding wastage prior to the transient. The corrosive layer is increased from zero to the set value during the pre-transient characterization and is kept as constant during the transient. The corroded outer layer of the cladding is assumed not to bear any applied load.