8.5. General Method of Solution
DEFORM‑4 is coupled to the rest of SAS4A through two main driver subroutines; SSFUEL for the pre‑transient calculation, and DFORM3 for the transient‑state calculations. In this manner, the DEFORM‑4 subroutines can be considered a separate code module which uses results from the SAS4A thermal/hydraulic calculation, temperatures and coolant pressures, and returns a new set of pin dimensions and properties. A general outline of this interaction scheme is shown in Figure 8.5.1.
In the integration of DEFORM‑4 into SAS4A, one of the primary considerations was to minimize the core storage and computational effort necessary when running a multichannel case with a long pre‑transient and transient sequence. Based on these considerations, it was decided to avoid the thermalmechanical iteration process and, instead, provide time‑step control for up to eight separate pre‑transient irradiation periods. This will be discussed in more detail below. In the transient state, the time steps are short enough to avoid the problem of inconsistent results between the thermal and mechanical calculations.
As Figure 8.5.1 shows, SAS4A performs thermal/hydraulic calculations over a specific time step in response to power and coolant conditions. During this time step, the dimensions are assumed to remain constant. SAS4A then passes to DEFORM‑4 the temperatures at the beginning and end of the time step, the final coolant pressures, and the length of the time step. DEFORM‑4 uses this information to calculate the fuel‑pin response to the temperature changes and returns to SAS4A a new set of dimensions consistent with the final thermal/hydraulic conditions. These new dimensions are then used in the calculation of the temperatures at the end of the next time step. In this manner SAS4A and DEFORM‑4 march through the entire pre‑transient and transient calculation.
The flowchart shown in Figure 8.5.2 illustrates the calling sequence in the pre‑transient driver, SSFUEL, and Fig. Figure 8.5.3 shows it in the transient driver, DFORM3. Each phenomenon considered is modularized into a separate subroutine. This makes the inclusion of new models and phenomena a very straightforward process of replacing or modifying specific subroutines. This same procedure has been followed in the incorporation of material properties, as outlined in Section 8.7. A number of the phenomena used in the pre‑transient calculation are not included in the transient calculation. Since the time scale of the transient is orders of magnitude less than the pre‑transient, phenomena such as pore migration and irradiation‑induced cladding swelling are assumed to be inactive, or less than second‑order effects. In this manner, the transient calculation is streamlined. If a particular case needs to include these phenomena in the transient, their inclusion is merely a matter of including the appropriate “CALL” statements in the transient driver routine.
For the mechanics calculation, the same routines are used in both the pre‑transient and transient calculation. In this way, the pre‑transient is considered an extended transient calculation. Since both states use the same routines, the use of computer storage is minimized. Also, since phenomenological changes take place that impact temperatures and dimensions, the pretransient is a special transient. In order to take maximum advantage of this basic structure, the ability to input ability to input up to eight different ramps or steady-state levels is incorporated into the SAS4A pre‑transient calculation. It is therefore possible to follow a simplified power history prior to the start of the transient.
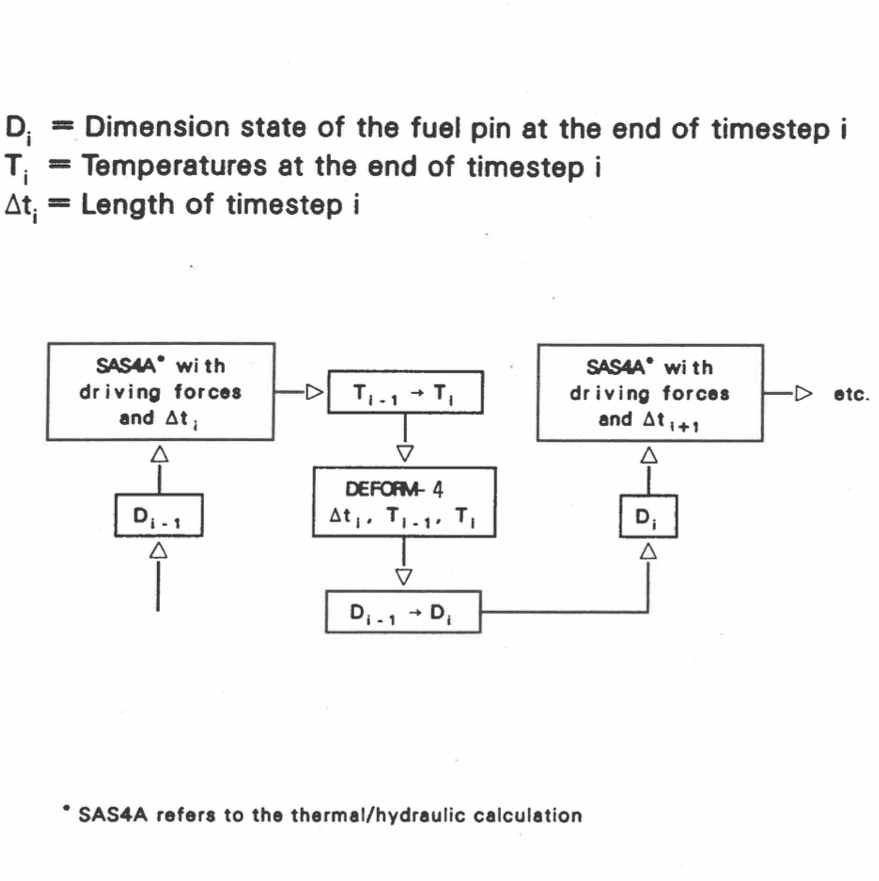
Figure 8.5.1 DEFORM-4 - SAS4A Time Step Interaction Scheme
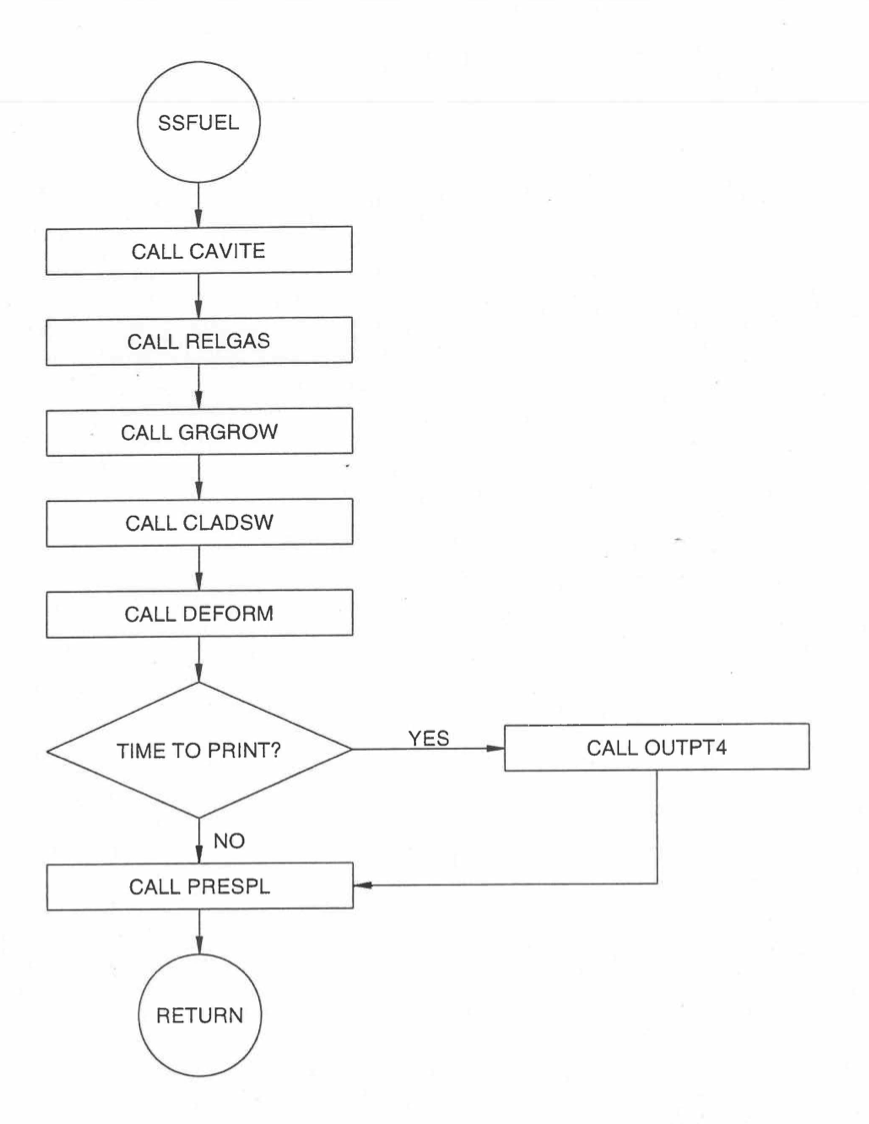
Figure 8.5.2 Pretransient DEFORM-4 Driver (SSFUEL) Flow Chart
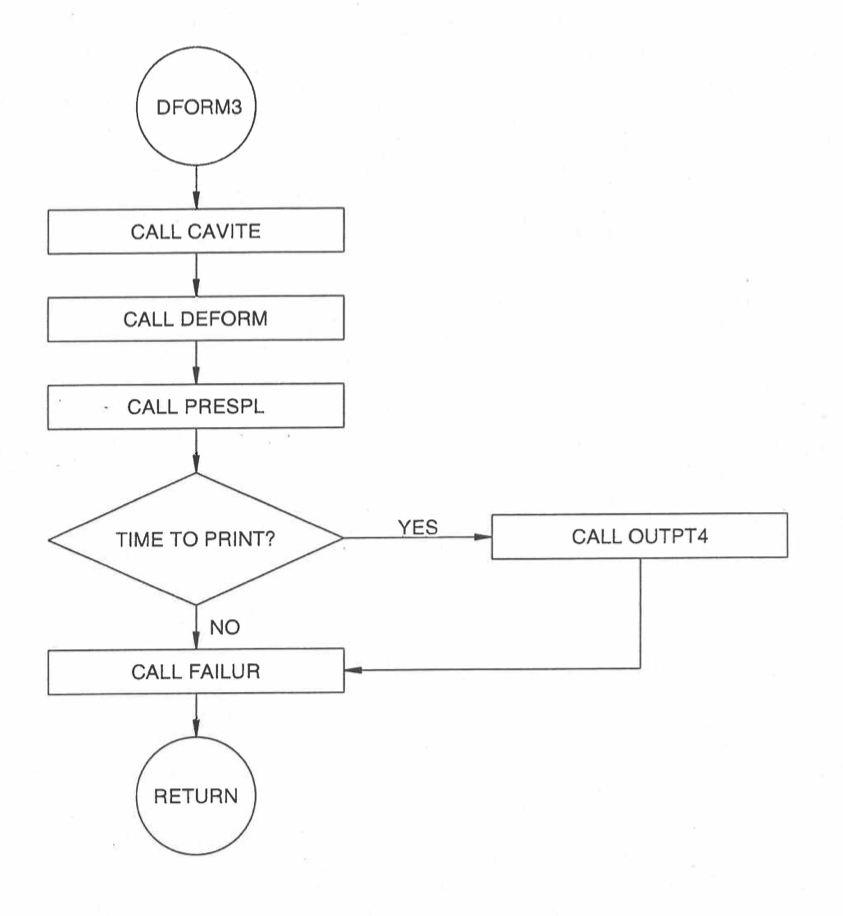
Figure 8.5.3 Transient DEFORM-4 Driver (DFORM3) Flow Chart
In the current version of DEFORM‑4, an approach has been adopted which separates the elastic and plastic deformation. These are linked through the fuel‑cladding interface pressure. The basic mechanics approach is through a generalized plane strain representation with an elastic cladding. The plastic deformation is derived from two sources. If the fuel‑cladding interface pressure produces cladding stresses below the flow stress, plastic deformation can occur through the process of creep. If the stresses induced exceed the flow stress, the cladding is assumed to behave in a perfectly plastic manner and the outer boundary condition on the fuel becomes the pressure that produces cladding stresses equal to the flow stress. In this situation, the radial deformation is determined by the fuel displacement until conditions return to the elastic state.
The calculations are performed on an axial segment by segment basis, starting at the lower axial blanket and continuing upward to the top axial blanket. A complete set of calculations for the response of the axial segment is performed before proceeding to the next segment.
8.5.1. Thermal-mechanical Solution
The thermal‑hydraulic routines in SAS4A provide DEFORM‑4 with the new coolant pressures and temperature in the fuel, cladding, coolant, and structure. DEFORM‑4 must then calculate the thermal‑mechanical response of the fuel‑cladding system to the changes during the time step. With the temperature changes and coolant pressure now from SAS4A, only one additional boundary condition remains as input to the calculation, the central cavity pressure. If no fuel melting has occurred, or the axial segment is not in the axial region considered to be the molten cavity, this pressure is set equal to the plenum pressure existing at the end of the previous time step. If molten fuel is present, then the axial pressure distribution is determined from the results of the molten cavity pressure subroutine CAVITE, see Section 8.3.7. This is the boundary force acting on the inner surface of the non‑molten fuel. The remaining force necessary to completely describe the external force system is the fuel‑cladding interface pressure, and this is determined through the iterative procedure described below.
In Figure 8.5.4, the main sequence of the mechanics driven routine, DEFORM, is illustrated. After initializing certain parameters, such as the thermal expansion strains, moduli of elasticity, etc., the fuel is checked to see if it is fully cracked or molten out to the cracked region. If a solid, non- cracked annulus of fuel still exists, the solid fuel elastic solution routine SOLID is called. If it is determined in this routine that the fuel becomes completely cracked during the time step, the crack fuel elastic solution routine MKDRIV is called. This routine would have been called initially if the fuel was completely cracked at the beginning of the time step.
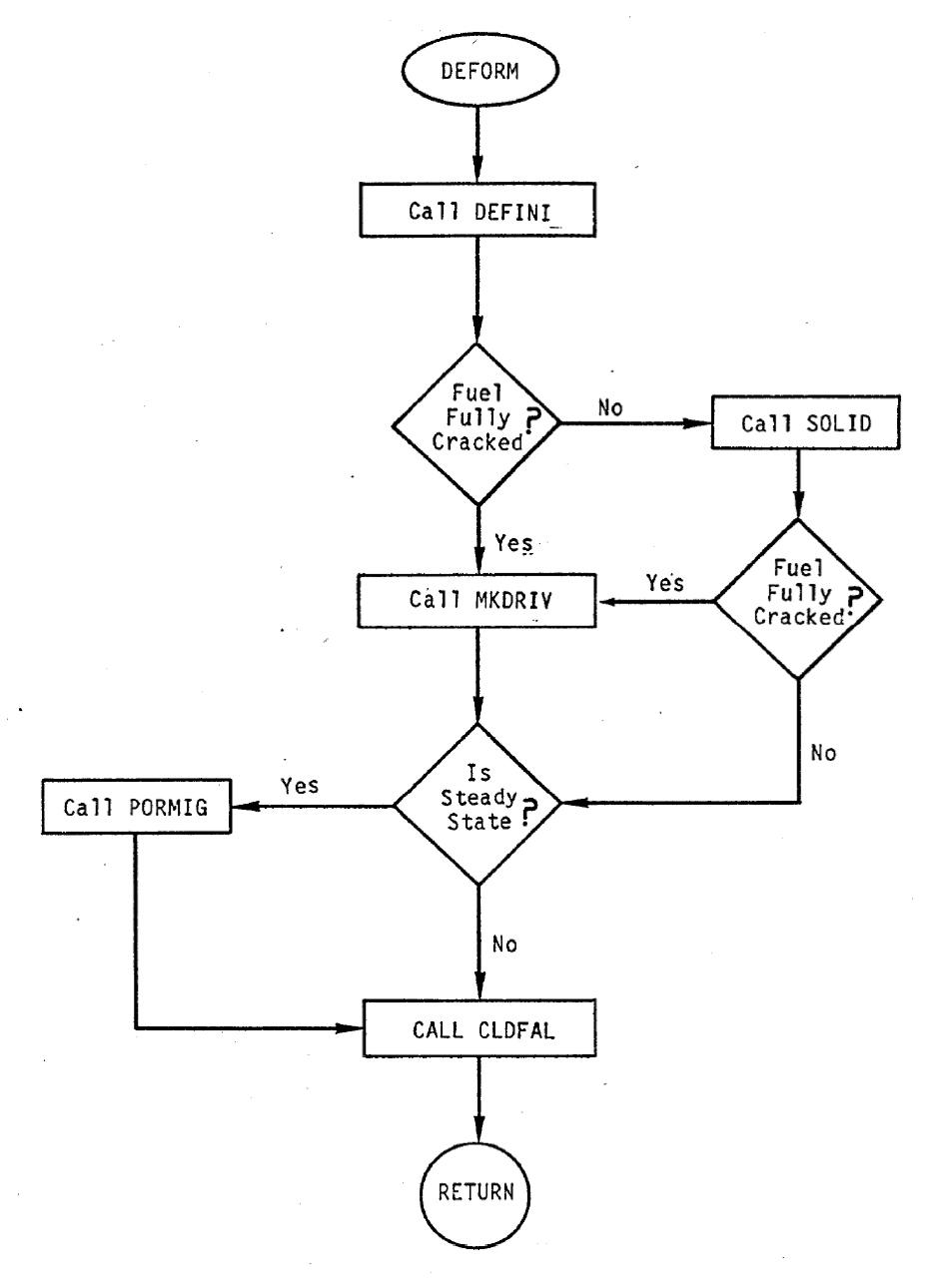
Figure 8.5.4 DEFORM-4 Mechanics driver (DEFORM) Flow Chart
The sequence of operations within the subroutine SOLID is shown in Figure 8.5.5. The main purpose of this routine is to determine the correct fuel-cladding interface pressure when a solid, uncracked fuel annulus exists at the beginning of the time step. Since the coolant pressure and central cavity pressure have been determined, SOLID must determine the fuel‑cladding interface pressure that produces consistency between the outer fuel surface and inner cladding surface locations.
The approach used in the solution procedure in SOLID is to recognize that the fuel‑cladding interface pressure is a bounded variable. It is, at least, the plenum pressure, but cannot exceed the value that would produce plastic flow in the cladding. SOLID therefore iterates to determine the value between these bounds that produces a consistent set of conditions. As a first estimate, the interface pressure from the previous time step is used. This, together with the thermal expansion in the current time step, is used to calculate the axial expansion in EXPAND, the non‑molten fuel stresses and strains in FSIGMA, the crack volume fraction in CRAKER, the cladding stresses and strains in CSIGMA, and the fuel swelling strains in FSWELL. Each of these routines calculate the incremental changes that occur from the previous time step results in response to the changes occurring during the current time step. If complete cracking of the fuel occurs during the time step, control is passed to the subroutine MKDRIV. If part of the fuel remains uncracked, then the new fuel‑cladding gap is examined to determine if a consistent set of conditions exists.
If a gap exists and the interface pressure is the plenum pressure, the solution is finished. If there is an interface pressure greater than the plenum pressure and the fuel‑cladding gap is zero, then the solution is finished. If there is a negative gap and the interface pressure produces the flow stress, the cladding is in plastic deformation and the fuel determines the deformation, so the solution is finished.
The more interesting case involves a negative gap with an interface pressure below that necessary to cause plastic deformation of the cladding. In this case the interface pressure is first set to that which would cause plastic flow, and the calculations are repeated. This second calculation through EXPAND, FSIGMA, CRAKER, CSIGMA, and FSWELL then provides the upper bound on the interface pressure. If the gap becomes positive, the correct value of the interface pressure is between the initial and the new estimate. Based on the changes in gap size as a function of the change in interface pressure, and the magnitude of the deformation necessary to produce a match of the outer fuel and inner cladding surfaces, a third estimate of the interface pressure is obtained assuming a linear relationship between interface pressure and gap size. This procedure is continued until a fuel‑cladding surface match is achieved within the desired tolerance or the fuel cracks completely.
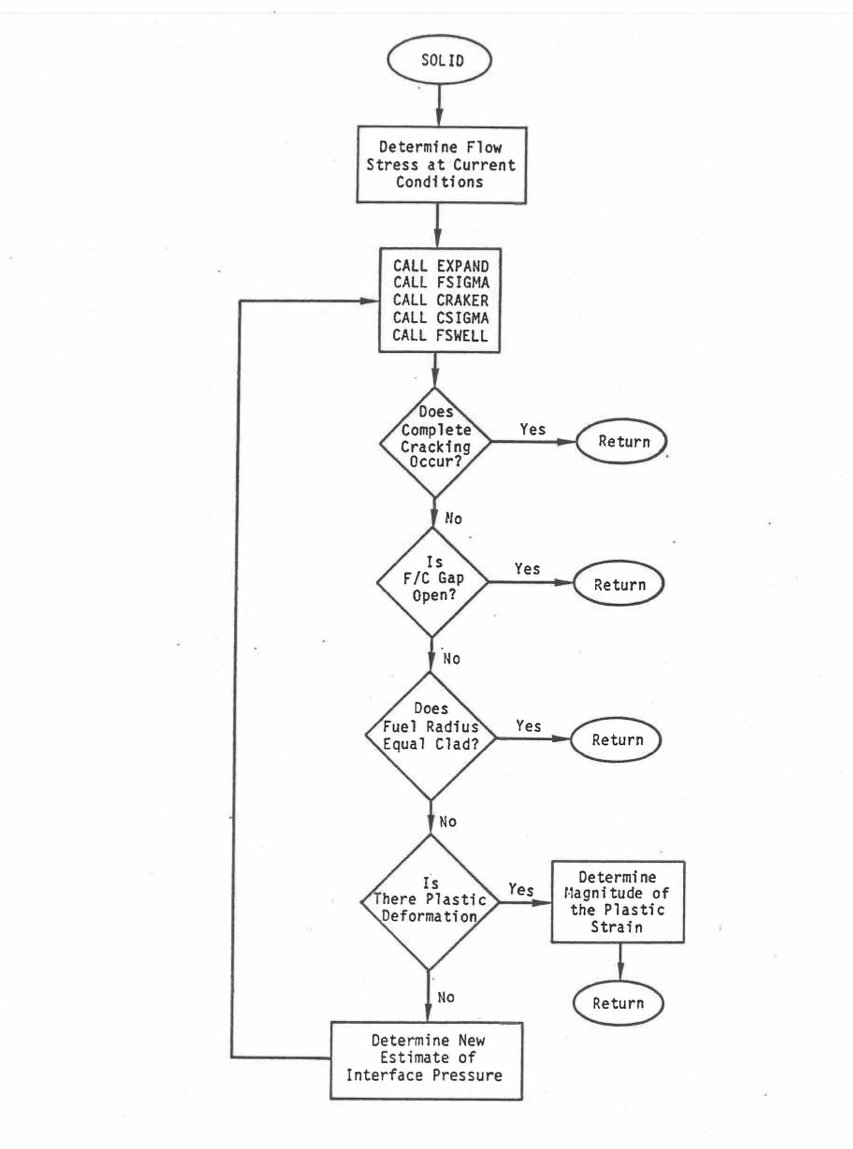
Figure 8.5.5 DEFORM-4 Mechanics Interaction Solution (SOLID) Flow Chart
When the applied interface pressure, cavity pressure, and thermal stresses produce a stress state in the fuel sufficient to cause the circumferential stress to exceed the fuel crack strength in a previously uncracked fuel cell, then the routine FSIGMA will redo its internal calculation with the new distribution of uncracked and cracked fuel cells. This routine will allow cracking to occur in all nodes where the circumferential stress exceeds the fracture strength. Prior to each invocation of EXPAND, FSIGMA, CRAKER, CSIGMA, and FSWELL, the crack state of the fuel is reset to the condition at the beginning of the time step.
In the case where all non‑molten fuel is cracked, the thermal‑mechanical solution is controlled by the subroutine MKDRIV. The sequence of operations for this routine is shown in Figure 8.5.6. There is no iteration because the fuel‑cladding interface pressure must be consistent with the cavity pressure and the solid fuel geometry. Knowing these two boundary conditions, the strains and fission gas induced swelling can be determined. If the fuel-cladding interface is open and the cavity pressure is equal to the plenum pressure, no movement of the cracked fuel takes place beyond the thermal-elastic and swelling strains. If the cavity is pressurized, the cracked fuel is translated radially to the cladding location. If the fuel‑cladding gap is negative, the fuel is moved inward to provide a match at the cladding location. In both cases, the crack volumes are adjusted to be consistent with the radial translation.
In the pre‑transient calculation, the cracked fuel is allowed to heal if the temperature is high enough. A healing temperature is determined based on the fuel solidus temperature.
where
TH = Crack healing temperature, K
fH = Input fraction
Ts = Fuel solidus temperature, K
If the fuel cell temperature is higher than this healing temperature, the cell is assumed to become solid again. This healing does not take place in the transient calculation where the time scale is too short.
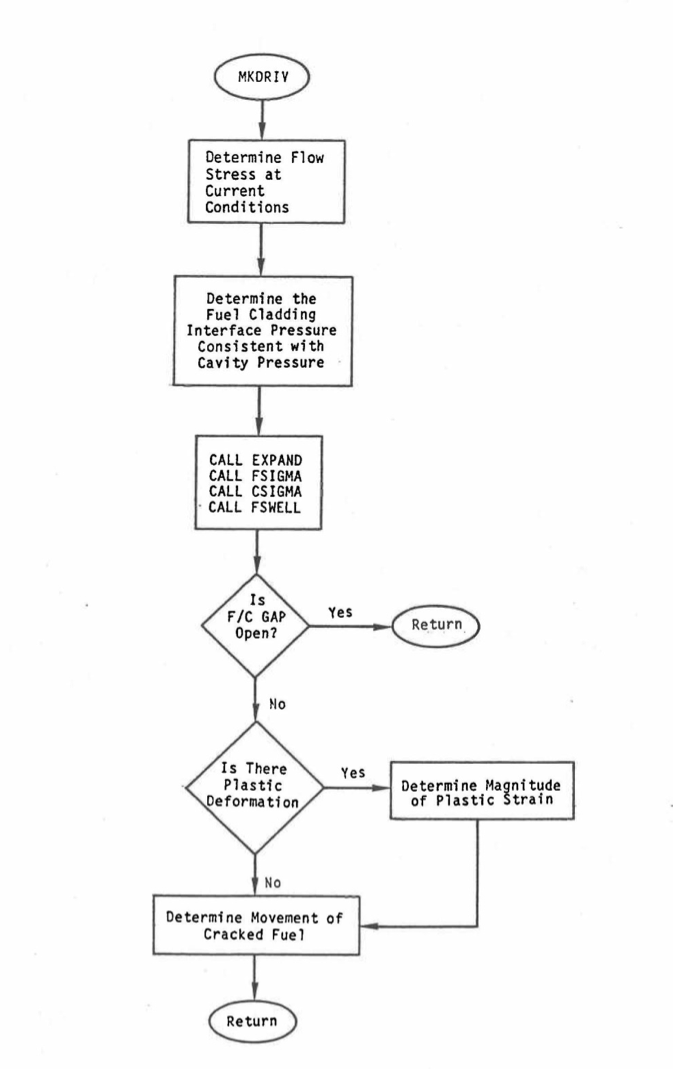
Figure 8.5.6 DEFORM-4 Mechanics Interaction Solution with Fully Cracked Fuel (MKDRIV) Flow Chart
8.5.2. Plastic Fuel Deformation Solution
The routine FSWELL handles all plastic fuel deformations. The basic equations for the non-equilibrium fission‑gas bubbles are given in Section 8.3.4.
First, the fuel hydrostatic pressure in each radial fuel node is calculated. The fission‑gas bubble swelling or hot pressing in each node is then determined. Once the swelling strains are known, the new fuel node boundaries are calculated.
In determining whether a fuel cell will move radially outward or inward, the concept of a plasticity temperature is used. If the fuel temperature is above the plasticity temperature, Tsep, it is assumed that the fuel is soft enough to be easily deformed and will move radially inward in response to the restriction of the cooler fuel. This softening temperature is defined as
where
Ts1 = Input base softening temperature, K
Ts2 = Pressure effect constant, K Pa-1
σfci = Fuel-cladding interface stress, Pa
The cooler fuel cells move radially outward. If the central void closes, the inner radius is fixed to a nominal zero value, 1×10−6, and all movement is radially outward. If the fuel is cracked across its entire radial extent, the movement is determined as described above.
In the molten cavity region, the volume changes calculated by CAVITE (see Section 8.3.7) are included in the redefinition of the node boundaries. In the solid nodes, the remaining as‑fabricated porosity and any fuel crack volume are included with the fission‑gas porosity in determining the new cell volumes. Once all the new node boundaries have been determined, the variation from the original is calculated and these node deformations are passed to the controlling solution routine.
Once a solution is obtained, all dimensions and stresses are updated to their final values, and the final plastic strain calculated (if any).
8.5.3. Final DEFORM-4 Calculations
After the thermal‑mechanical calculations are finished, DEFORM‑4 calculates the fuel axial expansion reactivity effects (see Section 8.3.9). The new plenum pressure, based on the new dimensions, temperatures, and fission gas release is then calculated in the subroutine PRESPL. The new gap conductance values for use in the next time step are determined. Control of the calculation is then returned to the SAS4A thermal/hydraulic routines for the calculation of the temperatures and coolant state for the next time step.