13.3. Method of Solution

13.3.1. CLAP Initialization and Cladding Meltthrough

The temperature and melt fraction of initial cladding are computed after the onset of boiling by the SAS fuel-pin model located in the subroutine TSHTRV and the calculation continues after CLAP initiation. This subroutine also contains the logical statements for CLAP initiation and cladding melt-through.

The first cladding to move is assumed to be the first axial segment that is completely molten; CLAP is initiated with this first melt-through. Any other axial segments join the molten cladding region if any one of its three radial segment nodes is molten; i.e., is above the liquidus temperature.

When entering CLAP (which uses coolant time steps) from a heat-transfer time step, a check is made to see whether any previously solid cladding nodes are now to be treated as molten cladding. If so, the total mass and energy of the initial, refrozen, and moving cladding are evaluated and these become the mass and energy of the moving cladding.

13.3.2. Solution of the Cladding Energy Equations

13.3.2.1. Interface with the Fuel-pin Model

There are slight differences in the thermodynamic representations of molten steel in the fuel-pin and CLAP models. In particular, the fuel-pin model in subroutine TSHTRV has a melting band (discrete solidus and liquidus temperatures) and a temperature-dependent specific heat, whereas CLAP has a single melting temperature and constant specific heats. If cladding temperatures from the fuel-pin model were used directly in CLAP calculations (for example, in adding segments to the molten region), then, possibly, energy would not be conserved due to differences in the thermodynamic models. To insure energy conservation, CLAP instead uses nodal energies rather than temperatures. A mean energy is computed from the SAS nodal energies:

(13.3-1)\[ {\overline{e}}_{\text{j}} = \frac{1}{4} e_{1,\text{j}} + \frac{1}{2} e_{2,\text{j}} + \frac{1}{4} e_{3,\text{j}}\]

where the \(e_{\text{i,j}}\)’s are the energies of the three radial nodes in axial segment \(j\). CLAP then evaluates the intact-cladding temperature \(T_{\text{i}}\) and melt fraction using \(\overline{e}\) and Eq. (13.2-49) to Eq. (13.2-51).

The fuel-pin model computes fuel temperatures in the molten cladding zone and both fuel and intact cladding temperatures for the remainder of the fueled section. For the molten zone, the CLAP routine integrates the fuel surface heat loss for each segment for a heat-transfer time interval:

(13.3-2)\[ Q_{\text{j}} = P_{\text{r}} \Delta z_{\text{j}} \int_{\text{t}^{*}}^{t^{*} + \Delta t^{*}}{\phi_{\text{c,j}}\text{dt}}\]

where

\(\Delta z_{\text{j}} = z_{\text{j}+1} - z_{\text{j}}\)

\(t^{*}\) is time at start of current heat-transfer time step

\(\Delta t^{*}\) is current heat-transfer time interval

\(\phi_{\text{c}}\) is the heat flux given by Eq. (13.2-32)

\(z_{\text{j}}\) is the elevation at the bottom of the “\(j\)”th segment.

This heat loss is utilized at the outer fuel boundary condition by the fuel-pin model. In a similar fashion, the heat loss from the outer surface of an intact cladding segment is computed by

(13.3-3)\[ Q_{\text{j}} = P_{\text{e}} \Delta z_{\text{j}} \int_{\text{t}^{*}}^{t^{*} + \Delta t^{*}}{\phi_{\text{r,j}} \text{dt}}\]

where \(\phi_{\text{r}}\) is the heat flux from Eq. (13.2-37) or Eq. (13.2-44), depending upon the configuration. This heat loss becomes part of the outer cladding boundary condition in the fuel-pin model, being added to the coolant heat loss, if any.

13.3.2.2. Intact and Refrozen Cladding

For this configuration, we set φ = 0 (adiabatic outer boundary) in the refrozen cladding energy Eq. (13.2-28). The energy equation is then combined with Eq. (13.2-37) and Eq. (13.2-49) to give

(13.3-4)\[ \frac{\text{dT}_{\text{s,j}}}{\text{dt}} = \xi_{1} \left( T_{\text{i}} - T_{\text{s}} \right) \bigg\rvert_{\text{j}}\]

where

\[\xi_{1,\text{j}} = \frac{P_{\text{e}} k_{\text{c}}}{\left\lbrack A_{\text{s}}\rho_{\text{s}} c_{\text{ps}}\left( \Delta r_{\text{s}} + \Delta r_{\text{i}} \right) \right\rbrack \bigg\rvert_{\text{j}}}\]

Since Eq. (13.2-28) has been reduced from a general field equation to a nodal equation, it becomes an ordinary differential equation (in time) in the process. The subscript \(j\), of course, denotes the axial segment number for which the parameter is evaluated.

Eq. (13.3-4) is converted to an implicit finite difference equation by substituting for the left side, the following:

(13.3-5)\[ \frac{\text{dT}_{\text{s,j}}}{\text{dt}} \approx \frac{T_{\text{s,j}}^{n}}{d}\]

and by evaluating \(T_{\text{s,j}}\) on the right side at the advanced time

(13.3-6)\[ T_{\text{s,j}}^{n + 1} = T_{\text{s,j}}^{n} + \Delta T_{\text{s,j}}^{n}\]

giving (after some rearrangement):

(13.3-7)\[ T_{\text{s,j}}^{n} = \frac{\xi_{1}\left( T_{\text{i}} - T_{\text{s}} \right)t}{1 + \xi_{1} t} \bigg\rvert_{\text{j}}^{n}\]

The implicit form is used rather than an explicit solution because it is stable for large \(\xi_{1}\) (or small \(A_{\text{s}}\)) and a reasonably sized \(\Delta t\).

The heat flux \(\phi_{\text{r}}\), required for the fuel-pin boundary condition Eq. (13.3-3) is evaluated from the energy equation:

(13.3-8)\[ \phi_{\text{r,j}}^{n} = \frac{A_{\text{s}}\rho_{\text{s}}C_{\text{ps}}\Delta T_{\text{s}}}{P_{\text{e}} \Delta t} \bigg\rvert_{\text{j}}^{n}\]

13.3.2.3. Evaluation of Convective Term in the Moving Cladding Energy Equation

The CLAP model uses a modified donor cell technique developed by Bohl [13-2] for the evaluation of the convective term

(13.3-9)\[ C_{\text{v}} = A_{\text{c}} \rho_{\text{c}}v_{\text{c}}\frac{\partial \text{e}_{\text{c}}}{\partial \text{z}}\]

in Eq. (13.2-25). This scheme uses a segment boundary mass flow \(w^{*}\) which is estimated by

(13.3-10)\[ w_{\text{j}}^{*} = \frac{1}{2}\left\lbrack A_{\text{c,j} - 1}\rho_{\text{c,j} - 1} v_{\text{c,j} - 1} + A_{\text{c,j}}\rho_{\text{c,j}}v_{\text{c,j}} \right\rbrack\]

The flow direction is determined by a mean flow \(w_{\text{m}}\):

(13.3-11)\[ w_{\text{m,j}} = \frac{1}{2}\left( \text{w}_{\text{j}}^{*} + w_{\text{j} + 1}^{*} \right)\]

The recipe for the convective term for a unblocked segment is as follows

(13.3-12)\[ \begin{aligned} C_{\text{v,j}} = w_{\text{j}}^{*} \frac{e_{\text{c,j}} - e_{\text{c,j} - 1}}{z_{\text{m,j}} - z_{\text{m,j} - 1}} && \text{for } w_{\text{m,j}} > 0, w_{\text{j}}^{*} > 0 \end{aligned}\]

(13.3-13)\[ \begin{aligned} C_{\text{v,j}} = w_{\text{j} + 1}^{*}\frac{e_{\text{c,j} + 1} - e_{\text{c,j}}}{z_{\text{m,j} + 1} - z_{\text{m,j}}} && \text{for } w_{\text{m,j}} < 0, w_{\text{j} + 1}^{*} < 0 \end{aligned}\]

(13.3-14)\[ \begin{aligned} C_{\text{v,j}} = 0, && \text{otherwise} \end{aligned}\]

The parameter \(z_{\text{m,j}}\) is the nodal elevation, which is related to the segment interface elevations \(z_{\text{j}}\) by

(13.3-15)\[ z_{\text{m,j}} = \frac{1}{2} \left( z_{\text{j}} + z_{\text{j} + 1} \right)\]

If the “\(j\)”th segment is nearly blocked, then the energy convection computed by Eq. (13.3-12) may be too large in magnitude. In this case, we define a segment flow \(w\) as

(13.3-16)\[ w_{\text{j}} = A_{\text{c,j}} \rho_{\text{c,j}} v_{\text{c,j}}\]

and compute the convective terms by (blocked segment only)

(13.3-17)\[ \begin{aligned} C_{\text{v,j}} = w_{\text{j}} \frac{e_{\text{c,j}} - e_{\text{c,j} - 1}}{z_{\text{m,j}} - z_{\text{m,j} - 1}} && \text{for } w_{\text{m,j}} > 0, w_{\text{j}} > 0 \end{aligned}\]

(13.3-18)\[ \begin{aligned} C_{\text{v,j}} = w_{\text{j}}\frac{e_{\text{c,j} + 1} - e_{\text{c,j}}}{z_{\text{m,j} + 1} - z_{\text{m,j}}} && \text{for } w_{\text{mj}} < 0, w_{\text{j}} > 0 \end{aligned}\]

(13.3-19)\[ \begin{aligned} C_{\text{v,j}} = 0, && \text{otherwise} \end{aligned}\]

The scheme also suppresses convection (sets \(C_{\text{v}} = 0\)) if the adjoining donor cell (either \(j-1\) or \(j+1\) depending on the sign of \(w_{\text{m}}\)) is blocked.

13.3.2.4. Moving Cladding on Bare Fuel

The outermost radial fuel node in the fuel-pin model is duplicated in CLAP for axial segments within the molten zone. The outer fuel temperature in CLAP, \(T_{\text{f}}\), is reset to the value computed by the pin model at the start of each heat-transfer time step. However, between heat transfer time steps, the fuel temperature is computed in CLAP; this is done primarily to achieve numerical stability, but it may also improve the accuracy of results. The configuration of the SAS outer fuel node and moving cladding is shown in Figure 13.3.1. The transient heat-balance equation for this outer node is

(13.3-20)\[ \pi\left( r_{\text{NR}}^{2} - r_{\text{NT}}^{2} \right)\rho_{\text{f}}c_{\text{pf}}\frac{\partial \text{T}_{\text{f}}}{\partial \text{t}} \ + 2\pi_{\text{NT}} k_{\text{f}} \frac{\partial \text{T}}{\partial \text{r}} \bigg\rvert_{\text{r}_{\text{NT}}} - \pi\left( r_{\text{NR}}^{2} \ - r_{\text{NT}}^{2} \right) Q_{\text{NT}} = - P_{\text{r}} h \left( T_{\text{f}} - T_{\text{c}} \right)\]

where reference to axial core segment \(j\) is tacitly implied.

It is assumed that the heat flow from the interior fuel nodes and the heat generated in the outer fuel node (given by the second and third terms in Eq. (13.3-20)) are relatively constant over one heat-transfer time step. We can therefore approximate these terms by evaluating them at the beginning of a heat-transfer time step. These terms are represented symbolically by the constant \(C_{\text{f}}\), defined by

(13.3-21)\[ \begin{aligned} C_{\text{f}} = 2\pi r_{\text{NT}} k_{\text{f}} \frac{\partial \text{T}}{\partial \text{r}} \bigg\rvert_{\text{r}_{\text{NT}}} - \pi\left( r_{\text{NR}}^{2} - r_{\text{NT}}^{2} \right) Q_{\text{NT}}, && \text{at } t = t^{*} \end{aligned}\]

where \(t^{*}\) is the beginning of the heat-transfer time step.

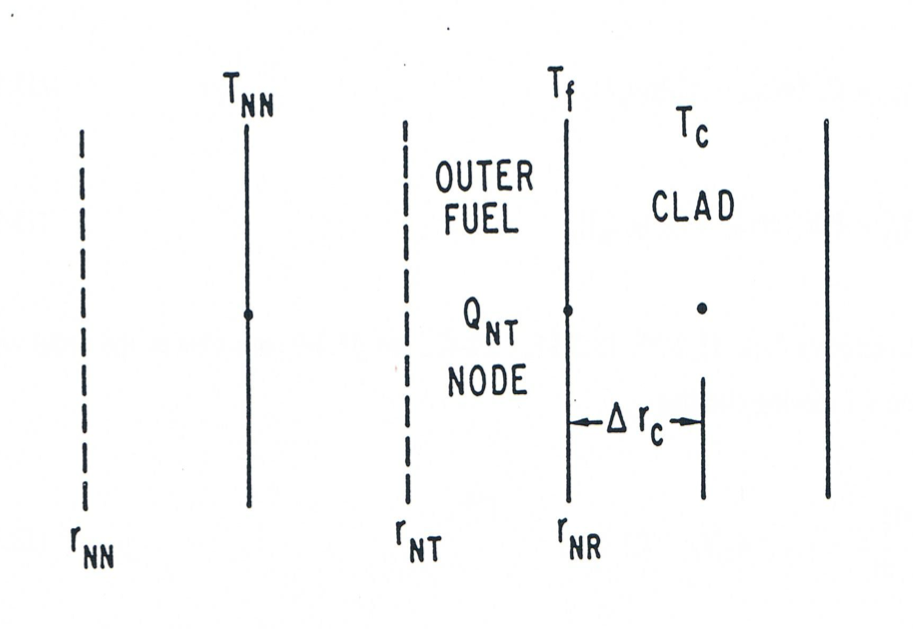
Figure 13.3.1 Schematic Showing the Interface of CLAP with the SAS Fuel Model

Because of the high heat-transfer coefficient to the molten cladding Eq. (13.2-33), the fuel-surface temperature and molten cladding temperature are closely coupled. For that reason, the term representing the instantaneous heat loss to the molten steel (on the right side of Eq. (13.3-20)) is retained as is, rather than incorporating it into the constant \(C_{\text{f}}\). Combining Eq. (13.3-20) and Eq. (13.3-21) and rearranging, we have

(13.3-22)\[ \frac{\text{dT}_{\text{f,j}}}{\text{dt}} + \gamma_{\text{f}} = - \xi_{\text{f}} \left( T_{\text{f}} - T_{\text{c}} \right) \bigg\rvert_{\text{j}}\]

where

(13.3-23)\[ \gamma_{\text{f,j}} = \frac{C_{\text{f}}}{\left\lbrack \pi\left( r_{\text{NR}}^{2} - r_{\text{NT}}^{2} \right) \right\rbrack}\rho_{\text{f}}c_{\text{pf}} \bigg\rvert_{\text{j}}\]

(13.3-24)\[ \xi_{\text{f,j}} = \frac{P_{\text{r}} h}{\left\lbrack \pi\left( r_{\text{NR}}^{2} - r_{\text{NT}}^{2} \right)\rho_{\text{f}}c_{\text{pf}} \right\rbrack \bigg\rvert_{\text{j}}}\]

Combining Eq. (13.2-25), Eq. (13.2-32), Eq. (13.2-50), and Eq. (13.3-9), one obtains the nodal energy equation for moving cladding:

(13.3-25)\[ \frac{\text{dT}_{\text{c,j}}}{\text{dt}} + \gamma_{\text{c,j}} = \xi_{2} \left( T_{\text{f}} - T_{\text{c}} \right) \bigg\rvert_{\text{j}}\]

where

(13.3-26)\[ \gamma_{\text{c,j}} = \frac{C_{\text{v}}}{\left( A_{\text{c}}\rho_{\text{c}}c_{\text{pc}} \right) \bigg\rvert_{\text{j}}}\]

(13.3-27)\[ \xi_{2,\text{j}} = \frac{P_{\text{r}} h}{\left( A_{\text{c}}\rho_{\text{c}}c_{\text{pc}} \right) \bigg\rvert_{\text{j}}}\]

Eq. (13.3-22) and Eq. (13.3-25) are converted to time-implicit difference equations by approximating the time derivatives according to

(13.3-28)\[ \frac{\text{dT}_{\text{f,j}}}{\text{dt}} \simeq \frac{\Delta T_{\text{f,j}}^{n}}{\Delta t^{n}}\]

(13.3-29)\[ \frac{\text{dT}_{\text{c,j}}}{\text{dt}} \simeq \frac{\Delta T_{\text{c,j}}^{n}}{\Delta t^{n}}\]

and evaluating the temperatures on the right-hand side at the advanced time \(t^{n+1}\). After substituting

(13.3-30)\[ T_{\text{c,j}}^{n + 1} = T_{\text{f,j}}^{n} + \Delta T_{\text{f,j}}^{n}\]

(13.3-31)\[ T_{\text{c,j}}^{n + 1} = T_{\text{c,j}}^{n} + \Delta T_{\text{c,j}}^{n}~ ,\]

the two difference equations are solved simultaneously for \(\Delta T_{\text{f}}\) and \(\Delta T_{\text{c}}\) and second-order terms in \(\Delta t\) are discarded, with the following results

(13.3-32)\[ \Delta T_{\text{c,j}}^{n} = - \frac{\left\lbrack \xi_{2}\left( T_{\text{f}} - T_{\text{c}} \right) - \gamma_{\text{c}} \right\rbrack \Delta t}{1 + \left( \xi_{2} + \xi_{\text{f}} \right) \Delta t} \bigg\rvert_{\text{j}}^{n}\]

(13.3-33)\[ \Delta T_{\text{f,j}}^{n} = - \frac{\left\lbrack \xi_{\text{f}}\left( T_{\text{f}} - T_{\text{c}} \right) - \gamma_{\text{f}} \right\rbrack \Delta t}{1 + \left( \xi_{2} + \xi_{\text{f}} \right) \Delta t} \bigg\rvert_{\text{j}}^{n}\]

The heat flux \(\phi_{\text{c}}\), which is needed to evaluate the integral in Eq. (13.3-2), is computed using a finite difference form of the moving clad energy Eq. (13.2-25):

(13.3-34)\[ \phi_{\text{c}} = \frac{C_{\text{v}}}{P_{\text{r}}} + \frac{A_{\text{c}}\rho_{\text{c}}c_{\text{pc}}\Delta T_{\text{c}}}{P_{\text{r}} \Delta t}\]

13.3.2.5. Moving Cladding on Intact and Refrozen Cladding

The nodal energy equation for the moving cladding for this configuration is obtained by combining Eq. (13.2-25), Eq. (13.2-39), Eq. (13.2-50), and Eq. (13.3-9), giving

(13.3-35)\[ \frac{\text{dT}_{\text{c,j}}}{\text{dt}} + \gamma_{\text{c}} = \xi_{2} \left( T_{\text{m}} - T_{\text{c}} \right) \bigg\rvert_{\text{j}}\]

where \(\gamma_{\text{c}}\) and \(\xi_{2}\) are defined in Eq. (13.3-26) and Eq. (13.3-27).

Solving this equation implicitly, i.e., replacing \(T_{\text{c}}\) by the updated value, approximating the time derivative by Eq. (13.3-29), and solving for \(\Delta T_{\text{c}}\), we get

(13.3-36)\[ \Delta T_{\text{c,j}}^{n} = - \frac{\left\lbrack \xi_{2}\left( T_{\text{m}} - T_{\text{c}} \right) - \gamma_{\text{c}} \right\rbrack \Delta t}{1 + \xi_{2} \Delta t} \bigg\rvert_{\text{j}}^{n}\]

The equation for the refrozen cladding temperature is found by substituting Eq. (13.2-37), Eq. (13.2-38), and Eq. (13.2-49) into the energy Eq. (13.2-28), resulting in

(13.3-37)\[ \Delta T_{\text{c,j}}^{n} = - \frac{\left\lbrack \xi_{2}\left( T_{\text{m}} - T_{\text{c}} \right) - \gamma_{\text{c}} \right\rbrack \Delta t}{1 + \xi_{2} \Delta t} \bigg\rvert_{\text{j}}^{n}\]

where

(13.3-38)\[ \xi_{3} = \frac{P_{\text{r}} k_{\text{c}}}{A_{\text{s}}\rho_{\text{s}}c_{\text{ps}}\Delta r_{\text{s}}}\]

Converting Eq. (13.3-37) to a finite-difference, implicit equation and solving for \(\Delta T_{\text{s}}\), one obtains

(13.3-39)\[ \Delta T_{\text{s,j}}^{n} = - \frac{\left\lbrack \xi_{1}\left( T_{\text{i}} - T_{\text{s}} \right) - \xi_{3}\left( T_{\text{s}} - T_{\text{m}} \right) \right\rbrack \Delta t}{1 + \left( \xi_{1} + \xi_{3} \right) \Delta t} \bigg\rvert_{\text{j}}^{n}\]

The heat fluxes \(\phi_{\text{r}}\) and \(\phi_{\text{hf}}\) are required for the fuel-pin boundary conditions Eq. (13.3-3) and to evaluate the rate of melting Eq. (13.2-30). These are evaluated using discretized versions of the energy Eq. (13.2-25) and Eq. (13.2-28) after computing \(\phi_{\text{r}}\) from Eq. (13.2-37). Then \(\phi_{\text{hf}}\) is computed using Eq. (13.2-29).

Several constraints apply to \(\phi_{\text{hf}}\). For positive \(\phi_{\text{hf}}\) (melting), more cladding cannot melt than actually exists in a frozen state. This restriction can be expressed as

(13.3-40)\[ \phi_{\text{hf}} \leq \frac{A_{\text{s}}\rho_{\text{s}}\lambda_{\text{c}}}{\Delta t P_{\text{r}}}\]

In case \(\phi_{\text{hf}}\) is adjusted to satisfy Eq. (13.3-40), new values of \(\phi\), \(\phi_{\text{c}}\) and \(\phi_{\text{r}}\) are computed from discretized versions of energy Eq. (13.2-25) and Eq. (13.2-28), along with Eq. (13.2-29), the definition of \(\phi_{\text{hf}}\).

The constraint for negative \(\phi_{\text{hf}}\) (freezing) arises from the condition that more cladding cannot freeze then exists in the molten state. Expressed mathematically, the limit is

(13.3-41)\[ \phi_{\text{hf}} \geq - \frac{A_{\text{c}}\rho_{\text{c}}\lambda_{\text{c}}}{\Delta t P_{\text{r}}}\]

13.3.2.6. Intact and Moving Cladding

The molten cladding energy equation for this case is identical to that for the case of moving cladding on intact and refrozen cladding. The molten cladding temperature change is therefore given by Eq. (13.3-36), which is also displayed below

(13.3-42)\[ \Delta T_{\text{c,j}}^{n} = - \frac{\left\lbrack \xi_{2}\left( T_{\text{m}} - T_{\text{c}} \right) - \gamma_{\text{c}} \right\rbrack \Delta t}{1 + \xi_{2} \Delta t} \bigg\rvert_{\text{j}}^{n}\]

The quantities \(\phi_{1}, \phi_{2}\), and \(\phi_{\text{trial}}\) are computed from Eq. (13.2-41) to Eq. (13.2-43). Then \(\phi_{\text{hf}}\) and \(\phi_{\text{r}}\) are computed according to Eq. (13.2-44), which we repeat below

(13.3-43)\[ \begin{matrix} \phi_{\text{hf}} = 0, & \phi_{\text{r}} = \phi_{2} & \text{ for } \phi_{\text{trial}} \geq 0, \end{matrix}\]

(13.3-44)\[ \begin{matrix} \phi_{\text{hf}} = \phi_{\text{trial}}, & \phi_{\text{r}} = \phi_{1} & \text{ for } \phi_{\text{trial}} < 0. \end{matrix}\]

The case of \(\phi_{\text{trial}} \geq 0\) corresponds to melting of the initial cladding; the heat of fusion is included in \(\phi_{\text{r}}\) which is the negative of the heat flux to the pin surface.

For \(\phi_{\text{trial}} \leq 0\), we obtain a negative \(\phi_{\text{hf}}\) (freezing) which will result in the appearance of refrozen cladding during the current time step. The constraint given by Eq. (13.3-41) is checked and, if not satisfied, then (i) \(\phi_{\text{hf}}\) is set equal to the limit given by Eq. (13.3-41) and (ii) a new \(\phi_{\text{r}}\) is computed by

(13.3-45)\[ \phi_{\text{r}} = \phi_{2} + \phi_{\text{hf}}\]

13.3.2.7. Heat Loss to Structure

At the onset of cladding motion, the structure is still relatively cool and consequently constitutes a potentially significant heat sink for the refreezing of cladding, particularly in small experimental subassemblies. The local heat absorbed by the structure (per unit length and unit time) is given by

(13.3-46)\[ Q_{\text{s,j}}^{n} = \frac{\theta P_{\text{w}}\left( T_{\text{m}} - T_{\text{w}} \right)}{\frac{\Delta r_{\text{w}}}{k} + \frac{1}{h}}\]

where

\(\theta\) = multiplier on heat loss to structure (usually = 1)

\(P_{\text{w}}\) = heated perimeter of the structure

\(T_{\text{w}}\) = structure temperature

\(\Delta r_{\text{w}}\) = half-thickness of structure.

The present CLAP model allows for the indirect transfer of heat form the moving cladding to the structure by way of the frozen cladding. An adjustment to the refrozen clad temperature \(\Delta T_{\text{s}}\) is defined by

(13.3-47)\[ T_{\text{s,j}}^{n + 1} = {\hat{T}}_{\text{s,j}}^{n + 1} + \Delta{\hat{T}}_{\text{s,j}}^{n}\]

where \({\hat{T}}_{\text{s,j}}^{n + 1}\) is the unadjusted refrozen cladding temperature.

Normally, the temperature adjustment would be given by

(13.3-48)\[ \Delta {\hat{T}}_{\text{s,j}}^{n} = Q_{\text{s}}\frac{\Delta t}{A_{\text{s}}\rho_{\text{s}}c_{\text{ps}}} \bigg\rvert_{\text{j}}^{n}\]

However, this formulation would be unstable in the case of vanishing \(A_{\text{s}}\) or large \(\Delta t\). To achieve stability, we slightly alter the physics; in particular, \(T_{\text{m}}\) is replaced in Eq. (13.3-46) by \(T_{\text{s,j}}^{n + 1}\). This adjustment in \(T_{\text{s}}\) is made only for segments where moving cladding is present; and, for these segments, we would expect the frozen cladding temperature to be close to the melting temperature, and hence the error in this approximation would be small. With this modification the adjustment is given by

(13.3-49)\[ \Delta {\hat{T}}_{\text{s,j}}^{n} = \frac{\xi_{\text{w}}\Delta t^{n}\left( \Delta {\hat{T}}_{\text{s,j}}^{n + 1} - T_{\text{w}} \right)}{1 + \epsilon_{\text{w}}\Delta t^{n}}\]

where

(13.3-50)\[ \xi_{\text{w}} = \frac{\theta P_{\text{w}}}{A_{\text{s}}\rho_{\text{s}}C_{\text{ps}}\left( \frac{\Delta r_{\text{w}}}{k} + \frac{1}{h} \right)} \bigg\rvert_{\text{j}}^{n}\]

13.3.3. Refrozen Steel Area Calculation

The refrozen cladding mass conservation Eq. (13.2-26) with the source term given by Eq. (13.2-30) is rewritten in the form

(13.3-51)\[ \rho_{\text{s}}\frac{\partial \text{A}_{\text{s}}}{\partial \text{t}} = - \frac{P_{\text{r}}\phi_{\text{hf}}}{\lambda} - A_{\text{s}}\frac{\partial\rho_{\text{s}}}{\partial \text{t}}.\]

The finite difference form of this equation is

(13.3-52)\[ A_{\text{s,j}}^{n + 1} = A_{\text{s,j}}^{n} - \frac{\left\lbrack \frac{\phi_{\text{hf}}P_{\text{r}}}{\lambda}\Delta t \bigg\rvert_{\text{j}}^{n} + A_{\text{s,j}}^{n} \left( \rho_{\text{s,j}}^{n + 1} - \rho_{\text{s,j}}^{n} \right) \right\rbrack}{\rho_{\text{s,j}}^{n + 1}}\]

After the density \(\rho_{\text{s,j}}^{n + 1}\) is evaluated from \(T_{\text{s,j}}^{n + 1}\) using Eq. (13.2-46), then the area \(A_{\text{s,j}}^{n + 1}\) is computed using Eq. (13.3-52). The thickness of the refrozen steel layer is computed from its area by assuming that the refrozen steel forms an annular ring around the intact cladding.

13.3.4. Moving Cladding Area Calculation

The continuity Eq. (13.2-14) and source term Eq. (13.2-30) are rewritten as

(13.3-53)\[ \rho_{\text{c}}\frac{\partial \text{A}_{\text{c}}}{\partial \text{t}} = - A_{\text{c}} \frac{\partial\rho_{\text{c}}}{\partial \text{t}} - C_{\text{a}} + \frac{P_{\text{r}}\varphi_{\text{hf}}}{\lambda}\]

where

(13.3-54)\[ C_{\text{a}} = \frac{\partial}{\partial \text{z}}\left( \rho_{\text{c}}A_{\text{c}}v_{\text{c}} \right)\]

The finite difference form of this equation is given by

(13.3-55)\[ A_{\text{c,j}}^{n + 1} = A_{\text{c,j}}^{n} + \frac{\left\lbrack {- A}_{\text{c,j}}^{n}\left( \rho_{\text{c,j}}^{n + 1} - \rho_{\text{c,j}}^{n} \right) - C_{\text{a}}\Delta t_{\text{n}} \ + \frac{{P_{\text{r}}\phi}_{\text{hf}}\Delta t}{\lambda} \bigg\rvert_{\text{j}}^{n} \right\rbrack}{\rho_{\text{c,j}}^{n + 1}} + A_{\text{mod,j}}^{n}\]

where \(A_{\text{mod}}\) is a correction term, defined later.

The solution method uses donor-cell differencing to evaluate the convective term \(C_{\text{a}}\) in terms of the nodal fluxes \(w_{\text{j}}\) (see Eq. (13.3-16)) and nodal elevation (see Eq. (13.3-15)). Normally \(A_{\text{mod}} = 0\) and \(C_{\text{a}}\) is computed as follows

(13.3-56)\[ \begin{aligned} C_{\text{a}} = \frac{w_{\text{j}}^{n} - w_{\text{j} - 1}^{n}}{z_{\text{m,j}} - z_{\text{m,j} - 1}} && \text{for } w_{\text{m,j}} \geq 0 \end{aligned}\]

(13.3-57)\[ \begin{aligned} C_{\text{a}} = \frac{w_{\text{j} + 1}^{n} - w_{\text{j}}^{n}}{z_{\text{m,j} + 1} - z_{\text{m,j}}} && \text{for } w_{\text{m,j}} < 0 \end{aligned}\]

Modifications to this formulation are made (i) to prevent cladding transfer outside of the fuel and blanket region and (ii) to inhibit cladding transfer to flooded or blocked nodes; the modifications consist simply of setting the appropriate values of \(w_{\text{j}}\) equal to zero.

Additionally, adjustments must be made for the case where the molten cladding area exceeds the available area \(A_{\text{max}}\), defined by

(13.3-58)\[ A_{\text{max,j}}^{n + 1} = A_{\text{f,j}} - A_{\text{i,j}}^{n + 1} - A_{\text{s,j}}^{n + 1}\]

where

\(A_{\text{f}}\) = total area for cladding allowed by the fuel

\(A_{\text{i}}\) = area of the intact cladding (if any).

For the case where the computed \(A_{\text{c,j}}^{n + 1}\) exceeds \(A_{\text{max}}\), the following steps are taken: (i) the condition is flagged by setting \(\text{NFULL}_{\text{j}} = 1\) (initial value is 0), (ii) the molten cladding area \(A_{\text{c,j}}^{n + 1}\) is set equal to \(A_{\text{max}}\), and (iii) the computed area for the donor segment is later adjusted consistent with step (ii).

To accomplish step (iii), we first estimate the volume of cladding convected into segment \(j\), denoted by \(\Gamma_{\text{j}}\), from continuity considerations:

(13.3-59)\[ \Gamma_{\text{j}} \cong \left\lbrack A_{\text{max,j}}^{n + 1} - A_{\text{c,j}}^{n} - \frac{P_{\text{r}} \frac{\phi_{\text{hf}} \Delta t}{\lambda} \bigg\rvert_{\text{j}}^{n}}{\rho_{\text{c,j}}^{n + 1}} \right\rbrack \left( z_{\text{j} + 1 }z_{\text{j}} \right)\]

Rather than adjusting \(C_{\text{a}}\) for the donor cell, we instead set \(w_{\text{j}}\) (or \(w_{\text{j}+1}\)) equal to zero and compute a correction \(A_{\text{mod}}\), which is the area change (negative) due to the volume of fluid \(\Gamma_{\text{j}}\) transferred to the flooded cell. For example, for the case of the donor cell below the flooded cell we have

(13.3-60)\[ \begin{aligned} w_{\text{j}} = 0, A_{\text{mod,j} - 1}^{n} = - \frac{\Gamma_{\text{j}}}{\left( z_{\text{j}} - z_{\text{j} - 1} \right)} && \text{for } \text{NFULL}_{\text{j}} = 1, w_{\text{m,j} - 1} \geq 0. \end{aligned}\]

Similarly, for the case of the donor cell above the flooded cell we have

(13.3-61)\[ \begin{aligned} w_{\text{j} + 1} = 0, A_{\text{mod,j} + 1}^{n} = - \frac{\Gamma_{\text{j}}}{\left( z_{\text{j} + 2} - z_{\text{j} + 1} \right)}, && \text{for } \text{NFULL}_{\text{j}} = 1, w_{\text{m,j} + 1} < 0. \end{aligned}\]

13.3.5. Reactivity Calculation

The reactivity change due to cladding relocation is computed by

(13.3-62)\[ \Delta K = \sum_{\text{j}}\left( m_{\text{j}}^{n} - m_{\text{j}}^{o} \right) \cdot W_{\text{j}}\]

where

\(m_{\text{j}}^{n}\) = mass of cladding in the \(j\)-th segment

\(m_{\text{j}}^{o}\) = original mass of cladding in the \(j\)-th segment

\(W_{\text{j}}\) = cladding reactivity worth distribution.

In the molten region, the mass is computed by

(13.3-63)\[ m_{\text{j}}^{n} = A_{\text{c}}\rho_{\text{c}}\Delta z \bigg\rvert_{\text{j}}^{n}\]

(13.3-64)\[ \text{where }\Delta z_{\text{j}} = z_{\text{j} + 1} - z_{\text{j}}\]

Outside the molten region the mass is evaluated using

(13.3-65)\[ m_{\text{j}}^{n} = m_{\text{j}}^{0} + A_{\text{s}}\rho_{\text{s}}\Delta z \bigg\rvert_{\text{j}}^{n} + A_{\text{c}}\rho_{\text{c}} \Delta z \bigg\rvert_{\text{j}}^{n} .\]

Due to roundoff and other possible small errors, the total mass of cladding may not be absolutely conserved which, if left uncorrected, would create anomalous reactivity effects. To insure mass conservation, the computed mass distribution is renormalized by the following steps:

(13.3-66)\[ M^{n} = \sum_{\text{j}}{m_{\text{j}}^{n}} ,\]

(13.3-67)\[ M^{o} = \sum_{\text{j}}{m_{\text{j}}^{o}} ,\]

(13.3-68)\[ m_{\text{j}}^{n} \cdot \frac{M^{o}}{M^{n}} \rightarrow m_{\text{j}}^{n}\]

where the operation A → B indicates that A is substituted for B.

13.3.6. Moving Cladding Velocity Calculation

The cladding momentum equation is solved in a separate subroutine (TSCLD2) that is called after the coolant dynamics equations have been solved. The terms \(\frac{\partial \text{p}}{\partial \text{z}}\) and \(F_{\text{v}}\) in the cladding momentum equation are evaluated at time \(t_{\text{n}} + 1/2 \Delta t^{n}\) (by averaging values at \(t^{n}\) and \(t^{n+1}\)) to achieve maximum accuracy with respect to sodium-vapor-induced cladding accelerations.

The pin friction term, \(\left( \frac{\partial \text{p}}{\partial \text{z}} \right)_{\text{fr}}\), is evaluated at the end of the time step to obtain maximum stability under conditions of strongly accelerating thin cladding films. Substituting

(13.3-69)\[v_{\text{c,j}}^{n + 1} = v_{\text{c,j}}^{n} + \Delta v_{\text{c,j}}^{n}\]

into Eq. (13.2-17) and Eq. (13.2-18) and retaining only linear terms, we obtain an equation of the form

(13.3-70)\[ F_{\text{p,j}}^{n + 1} = y_{1,\text{j}}^{n} + y_{2,\text{j}}^{n} \Delta v_{\text{c,j}}^{n}\]

where

(13.3-71)\[ \begin{aligned} y_{1,\text{j}}^{n + 1} = \frac{32 \mu_{\text{c}} v_{\text{c}}}{D_{\text{c}}^{2}} \bigg\rvert_{\text{j}}^{n} && \text{for } \text{Re}_{\text{j}}^{n} < \left( \text{Re} \right)_{\text{break}} \end{aligned}\]

(13.3-72)\[ \begin{aligned} y_{2,\text{j}}^{n} = \frac{32 \mu_{\text{c}}}{D_{\text{c}}^{2}} \bigg\rvert_{\text{j}}^{n} && \text{for } \text{Re}_{\text{j}}^{n} < \left( \text{Re} \right)_{\text{break}} \end{aligned}\]

(13.3-73)\[ \begin{aligned} y_{1,\text{j}}^{n} = \frac{b_{\text{f}}\rho_{\text{c}}v_{\text{c}} \left| v_{\text{c}} \right|}{2D_{\text{c}}} \bigg\rvert_{\text{j}}^{n} && \text{for } \text{Re}_{\text{j}}^{n} \geq \left( \text{Re} \right)_{\text{break}} \end{aligned}\]

(13.3-74)\[ \begin{aligned} y_{2,\text{j}}^{n} = \frac{b_{\text{f}}\rho_{\text{c}} \left| v_{\text{c}} \right|}{D_{\text{c}}} \bigg\rvert_{\text{j}}^{n} && \text{for } \text{Re}_{\text{j}}^{n} \geq \left( \text{Re} \right)_{\text{break}} \end{aligned}\]

The parameter \(C_{\text{m}}\) is used to represent the momentum convective term

(13.3-75)\[ C_{\text{m,j}} = v_{\text{c}}\frac{\partial \text{v}_{\text{c}}}{\partial \text{z}} \bigg\rvert_{\text{j}}\]

This parameter is evaluated by alternative formulae depending upon whether the segment is filled with cladding. For \(\text{NFULL} \left( j \right)=1\), indicating a filled segment, the term is estimated by the formula

(13.3-76)\[ C_{\text{m,j}}^{n} = v_{\text{c,j}}^{n}\frac{\partial \text{v}_{\text{c}}}{\partial \text{z}} \bigg\rvert_{\text{j}}^{n + 1/2}\]

where the derivative \(\frac{\partial \text{v}_{\text{c}}}{\partial \text{z}}\) is obtained by rearranging the continuity equation:

(13.3-77)\[ \frac{\partial \text{v}_{\text{c}}}{\partial \text{z}} = \frac{1}{\rho_{\text{c}}A_{\text{c}}}\left\lbrack \frac{\phi_{\text{hf}}P_{\text{r}}}{\lambda} - \frac{\partial\left( \rho_{\text{c}} A_{\text{c}} \right)}{\partial \text{t}} - v_{\text{c}}\frac{\left( \rho_{\text{c}}A_{\text{c}} \right)}{\partial \text{z}} \right\rbrack\]

and evaluating at time \(t^{n} + 1/2 \Delta t^{n}\). Two alternative equations are obtained, one for each flow direction, as given by the following:

(13.3-78)\[\begin{split}\frac{\partial \text{v}_{\text{c}}}{\partial \text{z}_{\text{j}}} \bigg\rvert^{n + 1/2} = \frac{1}{\left( \rho_{\text{c,j}} A_{\text{c,j}} \right)^{n + 1/2}} \left\lbrack \frac{\phi_{\text{h}_{\text{f}}}P_{\text{r}}}{\lambda_{\text{c}}} \bigg\rvert_{\text{j}}^{n} - \rho_{\text{c,j}}^{n} \frac{A_{\text{c,j}}^{n + 1} - A_{\text{c,j}}^{n}}{\Delta t^{n}} \right. \\ \left. - A_{\text{c,j}}^{n}\frac{\rho_{\text{c,j}}^{n + 1} - \rho_{\text{c,j}}^{n}}{\Delta t^{n}} - v_{\text{c,j}}^{n}\frac{\left( \rho_{\text{c,j} + 1}A_{\text{c,j} + 1} \right)^{n + 1/2} - \left( \rho_{\text{c,j}}A_{\text{c,j}} \right)^{n + 1/2}}{z_{\text{j} + 1} - z_{\text{j}}} \right\rbrack\end{split}\]

for \(w_{\text{m,j}}^{n} < 0\)

(13.3-79)\[\begin{split}\frac{\partial \text{v}_{\text{c}}}{\partial \text{z}_{\text{j}}} \bigg\rvert^{n + 1/2} = \frac{1}{\left( \rho_{\text{c,j}}A_{\text{c,j}} \right)^{n + 1/2}} \left\lbrack \frac{\phi_{\text{h}_{\text{f}}}P_{\text{r}}}{\lambda_{\text{c}}} \bigg\rvert_{\text{j}}^{n} - \rho_{\text{c,j}}^{n}\frac{A_{\text{c,j}}^{n + 1} - A_{\text{c,j}}^{n}}{\Delta t^{n}} \right. \\ \left. - A_{\text{c,j}}^{n}\frac{\rho_{\text{c,j}}^{n + 1} - \rho_{\text{c,j}}^{n}}{\Delta t^{n}} - v_{\text{c,j}}^{n}\frac{\left( \rho_{\text{c,j} + 1}A_{\text{c,j} + 1} \right)^{n + 1/2} - \left( \rho_{\text{c,j}}A_{\text{c,j}} \right)^{n + 1/2}}{z_{\text{j} + 1} - z_{\text{j}}} \right\rbrack\end{split}\]

for \(w_{\text{m,j}}^{n} < 0\)

where quantities on the right-hand side of Eq. (13.3-78) and Eq. (13.3-79) with the superscript \(n + 1/2\) are evaluated at time \(t^{n} + \Delta t^{n/2}\) as follows

(13.3-80)\[\left( \ \ \right)^{n + 1/2} = 1/2 \left\lbrack \left( \ \ \right)^{n} + \left( \ \ \right)^{n + 1} \right\rbrack\]

For \(\text{NFULL}_{\text{j}} = 0\), indicating an unblocked segment, we use the identity

(13.3-81)\[v_{\text{c}} \frac{\partial \text{v}_{\text{c}}}{\partial \text{z}} = 1/2 \frac{\partial \text{v}_{\text{c}}^{2}}{\partial \text{z}}\]

and evaluate the momentum convection term as follows

(13.3-82)\[\begin{aligned} C_{\text{m,j}} = \frac{\frac{1}{2} \left\lbrack \left( v_{\text{c,j} + 1}^{n} \right)^{2} - \left( v_{\text{c,j}}^{n} \right)^{2} \right\rbrack}{\left( z_{\text{m,j} + 1} - z_{\text{m,j}} \right)} && \text{for } w_{\text{m,j}}^{n} < 0 \end{aligned}\]

(13.3-83)\[\begin{aligned} C_{\text{m,j}} = \frac{\frac{1}{2} \left\lbrack \left( v_{\text{c,j}}^{n} \right)^{2} - \left( v_{\text{c,j} - 1}^{n} \right)^{2} \right\rbrack}{\left( z_{\text{m,j}} - z_{\text{m,j} - 1} \right)} && \text{for } w_{\text{m,j}}^{n} \geq 0 \end{aligned}\]

The discretized version of he moving-cladding momentum Eq. (13.2-24), using the linear approximation for \(F_{\text{p}}\) Eq. (13.3-70), and the symbolic representation for the momentum convective term Eq. (13.3-75), is given by

(13.3-84)\[\begin{split}\left( \rho_{\text{c,j}} \right)^{n + 1/2} \left\lbrack \frac{\Delta v_{\text{c,j}}^{n}}{\Delta t^{n}} + C_{\text{m,j}} + g \right\rbrack = - \frac{\partial \text{P}}{\partial \text{z}} \bigg\rvert_{\text{j}}^{n + 1/2} - \frac{A_{\text{v}}}{A_{\text{c}}}F_{\text{v}} \bigg\rvert_{\text{j}}^{n + 1/2} - \\ y_{1,\text{j}}^{n} - y_{2,\text{j}}^{n} \Delta v_{\text{c,j}}^{n} - \begin{cases} \begin{aligned} 0 && \text{if freezing} && \text{(13.3‑78a)} \\ \frac{P_{\text{r,j}}^{n}{\phi}_{\text{hf,j}}^{n} \left( v_{\text{c,j}}^{n} + \Delta v_{\text{c,j}}^{n} \right)}{A_{\text{c,j}}^{n + 1/2}{\lambda}_{\text{c,j}}^{n}} && \text{if melting} && \text{(13.3‑78b)} \\ \end{aligned} \end{cases}\end{split}\]

Solving this equation for \(\Delta v_{\text{c}}\), one obtains the form used in the CLAP program.