13.2. Mathematical Model

13.2.1. Sodium Vapor Flow Model

The sodium vapor flow generates the axial pressure gradients and interfacial shear forces, which influence the motion of molten cladding. The cladding motion in turn changes flow areas, hydraulic diameters, and surface roughness which all affect the sodium vapor flow. The governing equations for the sodium vapor, while presented elsewhere (Section 12.6.1) in more detail, are reproduced here to show the intimate coupling between the sodium vapor dynamics and cladding motion. The conservation equations for the sodium vapor are

(13.2-1)\[ \frac{\partial}{\partial \text{t}} \left( A_{\text{v}} \rho_{\text{v}} \right) + \frac{ \partial \text{w}}{\partial \text{z}} = {\dot{m}}_{\text{v}}\]

(13.2-2)\[\begin{split} \frac{\partial \text{w}}{\partial \text{t}} + \frac{\partial}{\partial \text{z}}\left( \frac{w^{2}}{A_{\text{v}}} \rho_{\text{v}} \right) + A_{\text{v}}\left\lbrack \frac{\partial \text{p}}{\partial \text{z}} + F_{\text{v}} \right\rbrack \ = \begin{cases} \begin{aligned} {\dot{m}}_{\text{v}} \frac{w}{A_{\text{v}}} \rho_{\text{v}}, && \text{if condensing} && \text{(13.2‑2a)} \\ 0, && \text{if vaporizing} && \text{(13.2‑2b)} \end{aligned} \end{cases}\end{split}\]

where

\(A_{\text{v}}\) = vapor flow area

\(\rho_{\text{v}}\) = vapor density

\(w\) = vapor mass flowrate

\({\dot{m}}_{\text{v}}\) = the rate of vapor generation per unit length of channel

\(\frac{\partial \text{p}}{\partial \text{z}}\) = channel axial pressure gradient

\(F_{\text{v}}\) = cladding/vapor interfacial friction force per unit volume of vapor.

The friction force term is evaluated from the following equation:

(13.2-3)\[ F_{\text{v}} = \frac{f_{\text{sf}} M w \left| w \right|}{2 \rho_{\text{v}} A_{\text{v}}^{2} D_{\text{v}}}\]

where

\(f_{\text{sf}}\) = single-phase friction factor

\(M\) = flooding multiplier

\(D_{\text{v}}\) = hydraulic diameter for the vapor.

The hydraulic diameter is estimated by

(13.2-4)\[ D_{\text{v}} = D_{\text{h}} \sqrt{\alpha}\]

where

\(D_{\text{h}}\) = hydraulic diameter for bare fuel or fuel pin (depending upon the zone)

\(\alpha\) = vapor fraction based on area available for molten steel plus vapor.

This equation assumes that the hydraulic diameter \(D_{\text{v}}\) varies as the square root of the area \(_{\text{v}}\) (which would be exact for a circular vapor flow passage) and hence scales as the square root of vapor fraction (proportional to the flow area).

The smooth wall (single-phase) friction factor is given by

(13.2-5)\[ f_{\text{sf}} = \text{AFRV} \left( \text{Re} \right)_{\text{v}}^{\text{BFRV}}\]

(13.2-6)\[ \left( \text{Re} \right)_{\text{v}} = w \frac{D_{\text{v}}}{A_{\text{v}}} \mu_{\text{v}}\]

where

\(\text{AFRV}\), \(\text{BFRV}\) = input constants

\(\mu_{\text{v}}\) = vapor viscosity.

For consistency, the inputed constants AFRV and BFRV used in CLAP are identical to those used in the sodium voiding model.

The flooding multiplier is flow-regime dependent. The transition from smooth wall friction \(\left( M = 1 \right)\) to a chaotic two-phase flow structure (\(M = M_{2 \Phi}\), where \(M_{2 \Phi}\) is defined later) occurs nominally when the vapor velocity exceeds the flooding velocity. The current version of CLAP uses the correlation of Fauske, et al. [13-4]:

(13.2-7)\[ v_{\text{flood}} = \left\lbrack \frac{32}{3} \frac{\rho_{\text{c}} g \Delta r_{\text{c}}}{\rho_{\text{v}} f_{\text{sf}} M_{2 \Phi}} \right\rbrack^{1/2}\]

where

\(\Delta r_{\text{c}}\) = one-half the molten cladding thickness

\(\rho_{\text{c}}\) = molten cladding density.

The CLAP model has a hysteresis effect in the treatment of the flooding multiplier whereby flooding and the inverse, deflooding, occur at slightly different velocities as follows:

(13.2-8)\[ \begin{matrix} & \text{set } & M^{n} = M_{2 \Phi}, & \text{if } & M^{n - 1} = 1 & \text{and } & \left| \frac{w}{A_{\text{v}}} \rho_{\text{v}} \right| > 1.1 v_{\text{flood}} \end{matrix}\]

(13.2-9)\[ \begin{matrix} & \text{set } & M^{n} = 1, & \text{if } & M^{n - 1} = M_{2 \Phi} & \text{and } & \left| \frac{w}{A_{\text{v}}} \rho_{\text{v}} \right| < 0.9 v_{\text{flood}} \end{matrix}\]

where \(n\) is the current time-step number. If the conditions in either Eq. (13.2-8) or Eq. (13.2-9) are not met, then the previous value of \(M\) is retained.

The two-phase friction multiplier is given by

(13.2-10)\[ \begin{aligned} M_{2 \Phi} = I \cdot \left\lbrack 1 + \varepsilon \left( 1 - \alpha \right) \right\rbrack && \text{for } \alpha > \alpha_{\text{crit}} \end{aligned}\]

(13.2-11)\[ \begin{aligned} M_{2 \Phi} = I \cdot \left\lbrack 1 + \varepsilon \left( 1 - \alpha_{\text{crit}} \right) \right\rbrack && \text{for } \alpha \leq \alpha_{\text{crit}} \end{aligned}\]

where \(\varepsilon\) and \(\alpha_{\text{crit}}\) are input and \(I\) is an incoherence multiplier. For values of \(\varepsilon = 75\) and \(\alpha_{\text{crit}} = 0\), Eq. (13.2-10) is equivalent to the Wallis correlation [13-5].

Radial incoherency in cladding melting, which occurs during the early portion of cladding motion, results in a lower bundle pressure drop and lower cladding velocity than predicted by one-dimensional models that ignore this effect [13-6]. The incoherence multiplier allows for this incoherency effect by temporarily reducing the two-phase friction multiplier during early cladding motion in the following manner:

(13.2-12)\[ \begin{aligned} I = \left\lbrack \text{fps}{\left( \text{fps} \right)_{0}} \right\rbrack^{x} && \text{for } \text{fps} < \left( \text{fps} \right)_{0} \end{aligned}\]

(13.2-13)\[ \begin{aligned} I = 1 && \text{for } \text{fps} \geq \left( \text{fps} \right)_{0} \end{aligned}\]

where \(\text{fps}\) are full-power seconds since cladding first moved in a channel and \(\left( \text{fps} \right)_{0}\) and \(x\) are input constants.

The code sets \(M_{2 \phi}\) equal to unity, equivalent to a smooth wall friction factor, if the value of \(M_{2 \phi}\) computed by Eq. (13.2-10) is less than unity. Consequently, the effect of the multiplier “\(I\)” is to delay flooding by \(\left( \text{fps} \right)_{0}\) full-power seconds. For cases where the vapor velocity is below that necessary for flooding, neither \(\left( \text{fps} \right)_{0}\) nor \(\varepsilon\) will have any effect on the cladding motion. Values for \(\left( \text{fps} \right)_{0}\) and \(x\) of 0.3 and 3 are provisionally recommended; better values will be determined later by calibration of the CLAP model using experimental data.

13.2.2. Moving Cladding Basic Equations

The mass, momentum, and energy conservation equations for moving (molten) cladding are

(13.2-14)\[ \frac{\partial}{\partial \text{t}} \left( \rho_{\text{c}} A_{\text{c}} \right) + \frac{\partial}{\partial \text{z}} \left( \rho_{\text{c}} A_{\text{c}} v_{\text{c}} \right) = {\dot{m}}_{\text{c}}\]

(13.2-15)\[\begin{split} \frac{\partial}{\partial \text{t}} \left( \rho_{\text{c}} A_{\text{c}} c_{\text{c}} \right) + \frac{\partial}{\partial \text{z}} \left( \rho_{\text{c}} A_{\text{c}} v_{\text{c}}^{2} \right) + A_{\text{c}} \frac{\partial \text{p}}{\partial \text{z}} \ + A_{\text{c}} F_{\text{p}} - A_{\text{v}} F_{\text{v}} + A_{\text{c}} \rho_{\text{c}} g = \begin{cases} \begin{aligned} {\dot{m}}_{\text{c}} v_{\text{c}} && \text{if freezing} && \text{(13.2‑13a)} \\ 0, && \text{if melting} && \text{(13.2‑13b)} \end{aligned} \end{cases}\end{split}\]

(13.2-16)\[ \frac{\partial}{\partial \text{t}} \left( \rho_{\text{c}} A_{\text{c}} e_{\text{c}} \right) + \frac{\partial}{\partial \text{z}} \left( \rho_{\text{c}} A_{\text{c}} v_{\text{c}} e_{\text{c}} \right) = \phi_{\text{c}} P_{\text{r}} + {\dot{m}}_{\text{c}} e_{\text{c}}\]

\(A_{\text{c}}\) = moving cladding cross-sectional area

\(v_{\text{c}}\) = moving cladding velocity

\({\dot{m}}_{\text{c}}\) = mass rate of melting of substrate per unit length of channel (or rate of freezing if negative)

\(F_{\text{p}}\) = pin friction-force per unit volume of molten cladding

\(e_{\text{c}}\) = moving cladding internal energy

\(\phi_{\text{c}}\) = flux of sensible heat from the solid/liquid interface into the molten cladding

\(P_{\text{r}}\) = perimeter of solid/liquid interface.

The pin or bare-fuel friction force is evaluated by the following:

(13.2-17)\[ F_{\text{p}} = \frac{c_{\text{f}} \rho_{\text{c}} v_{\text{c}} \left| v_{\text{c}} \right|}{2 D_{\text{c}}}\]

where

\(c_{\text{f}}\) = pin friction factor

\(D_{\text{c}}\) = molten cladding hydraulic diameter.

The CLAZAS [13-3] formulation for the friction factor has been incorporated into CLAP:

(13.2-18)\[ \begin{aligned} c_{\text{f}} = \frac{64}{\text{Re}} && \text{for Re} < \left( \text{Re} \right)_{\text{break}} \end{aligned}\]

(13.2-19)\[ \begin{aligned} c_{\text{f}} = b_{\text{f}} && \text{for Re} \geq \left( \text{Re} \right)_{\text{break}} \end{aligned}\]

where Re is the molten-cladding Reynolds number defined by:

(13.2-20)\[ \text{Re} = \frac{D_{\text{c}} \rho_{\text{c}} \left| v_{\text{c}} \right|}{\mu_{\text{c}}}\]

\(\left( \text{Re} \right)_{\text{break}}\) is the critical Reynolds number for the transition from laminar to turbulent friction and \(b_{\text{f}}\) is the turbulent Moody friction factor. The CLAZAS derived values for \(\left( \text{Re} \right)_{\text{break}}\) and \(b_{\text{f}}\) of \(2.1 \times 10^{3}\) and \(2.0 \times 10^{-2}\) are currently recommended as input values.

The cladding viscosity depends upon the cladding temperature \(T_{\text{c}}\) and melt-fraction \(f\) as follows

(13.2-21)\[ \begin{aligned} \mu_{\text{c}} = \mu_{\text{m}} \exp\left( \frac{a}{T_{\text{c}}} - \frac{a}{T_{\text{m}}} \right) && \text{for } T_{\text{c}} > T_{\text{m}} \end{aligned}\]

(13.2-22)\[ \begin{aligned} \mu_{\text{c}} = \left( \mu_{\text{t}} - \mu_{\text{m}} \right) \left( 1 - f \right)^{q} + \mu_{\text{m}} && \text{for } T_{\text{c}} = T_{\text{m}} \end{aligned}\]

(13.2-23)\[ \begin{aligned} \mu_{\text{c}} = \mu_{\text{s}} && \text{for } T_{\text{c}} < T_{\text{m}} \end{aligned}\]

where \(T_{\text{m}}\) is the cladding melting temperature, \(\mu_{\text{s}}\), \(\mu_{\text{t}}\), \(\mu_{\text{m}}\) are the user-supplied viscosities for solid cladding, at the solidus temperature, and cladding at the liquidus temperature, and \(a\) and \(q\) are input constants. Values for \(\mu_{\text{m}}\) and \(a\) of \(6.42 \times 10^{-3}\) Pa-s and 5492 K are recommended [13-7]. The input parameters \(\mu_{\text{t}}, \mu_{\text{s}}\), and \(q\) are not properties per se, but are constants in a phenomenological model and hence need to be determined by calibration with cladding motion test data. In general, the values selected for \(\mu_{\text{t}}\) and \(\mu_{\text{s}}\) should be sufficiently large to effectively arrest cladding motion for solid cladding. Provisional values for both \(\mu_{\text{t}}\) and \(\mu_{\text{s}}\) of \(10^{4}\) Pa-s (\(10^{5}\) poise), from the CLAZAS sample problem [13-3], and for \(q\) of 0.5 are recommended.

The momentum and energy Eq. (13.2-15) and Eq. (13.2-16) are converted to non-conservative form using Eq. (13.2-14), giving the following:

(13.2-24)\[\begin{split}\rho_{\text{c}}\left\lbrack \frac{\partial \text{v}_{\text{c}}}{\partial \text{t}} + v_{\text{c}}\frac{\partial \text{v}_{\text{c}}}{\partial \text{t}} \right\rbrack + \frac{\partial \text{p}}{\partial \text{z}} + F_{\text{p}} - \frac{A_{\text{v}}}{A_{\text{c}}} F_{\text{v}} + g \rho_{\text{c}} = \begin{cases} \begin{aligned} 0 && \text{if freezing} && \text{(13.2‑19a)} \\ - m_{\text{c}} \frac{{\dot{v}}_{\text{c}}}{A_{\text{c}}} && \text{if melting} && \text{(13.2‑19b)} \end{aligned} \end{cases}\end{split}\]

(13.2-25)\[ \frac{\partial \text{e}_{\text{c}}}{\partial \text{t}} + v_{\text{c}} \frac{\partial \text{e}_{\text{c}}}{\partial \text{z}} = \frac{\phi_{\text{c}} P_{\text{r}}}{A_{\text{c}}\rho_{\text{c}}}\]

13.2.3. Refrozen Cladding Basic Equations

The conservation equations for the refrozen steel layer are

(13.2-26)\[ \frac{\partial}{\partial \text{t}}\left( \rho_{\text{s}} A_{\text{s}} \right) = - {\dot{m}}_{\text{c}}\]

(13.2-27)\[ \frac{\partial}{\partial \text{t}}\left( \rho_{\text{s}} A_{\text{s}} e_{\text{s}} \right) = \phi_{\text{r}} P_{\text{e}} - \phi P_{\text{r}} - {\dot{m}}_{\text{e}} e_{\text{s}}\]

where

\(\rho_{\text{s}}\) = refrozen steel density

\(A_{\text{s}}\) = refrozen steel cross-sectional area

\(e_{\text{s}}\) = refrozen steel internal energy

\(\phi_{\text{r}}\) = heat flux at the interface between intact cladding and refrozen cladding

\(P_{\text{e}}\) = outer perimeter of intact cladding

\(\phi\) = flux of sensible heat from the refrozen cladding to the melt (solid/liquid) interface.

Recall that the quantity \({\dot{m}}_{\text{c}}\) was the rate of melting (negative for freezing) and hence appears as a sink (negative sign) in the refrozen cladding Eq. (13.2-26) and Eq. (13.2-27).

By manipulating the preceding equations, we obtain the nonconservative form of the energy equation:

(13.2-28)\[ \frac{\partial \text{e}_{\text{s}}}{\partial \text{t}} = \frac{\left( \phi_{\text{r}} P_{\text{e}} - \phi P_{\text{r}} \right)}{\rho_{\text{s}}A_{\text{s}}}\]

Note that the sensible heat fluxes on either side of the melt layer are not the same (see Figure 13.2.1). The difference \(\phi_{\text{hf}}\) is the heat flux for fusion, defined by

(13.2-29)\[ \phi_{\text{hf}} = \phi - \phi_{\text{c}}\]

The rate of melting (or freezing, if negative) is directly related to the fusion heat flux:

(13.2-30)\[ {\dot{m}}_{\text{c}} = P_{\text{r}} \frac{\phi_{hf}}{\lambda}\]

where \(\lambda\) is an effective heat of fusion of the cladding defined as

(13.2-31)\[ \lambda = e_{\text{c}} - e_{\text{s}}\]

13.2.4. Heat-transfer Relationships

13.2.4.1. Moving Cladding on Bare Fuel

The configuration in the molten zone is shown in Figure 13.2.1. There is no solid cladding in this region and, therefore, the heat flux for melting, \(\phi_{\text{hf}}\), is zero. The sensible heat flux is given by

(13.2-32)\[ \phi_{\text{c}} = h \left( T_{\text{f}} - T_{\text{c}} \right)\]

where

\(T_{\text{f}}\) = fuel pellet surface temperature

\(h\) = coefficient of heat transfer from the fuel to molten cladding.

The heat-transfer coefficient for the moving cladding is defined from a correlation for liquid-metal heat transport as

(13.2-33)\[ \frac{h D_{\text{c}}}{k_{\text{c}}} = C_{1} \left( D_{\text{c}} \rho_{\text{c}} c_{\text{pc}} \frac{\left| v_{\text{c}} \right|}{k_{\text{c}}} \right)^{C_{2}} + C_{3}\]

where

\(k_{\text{c}}\) = molten cladding thermal conductivity

\(c_{\text{pc}}\) = molten cladding specific heat capacity

\(C_{1}, C_{2}, C_{3}\) = input constants.

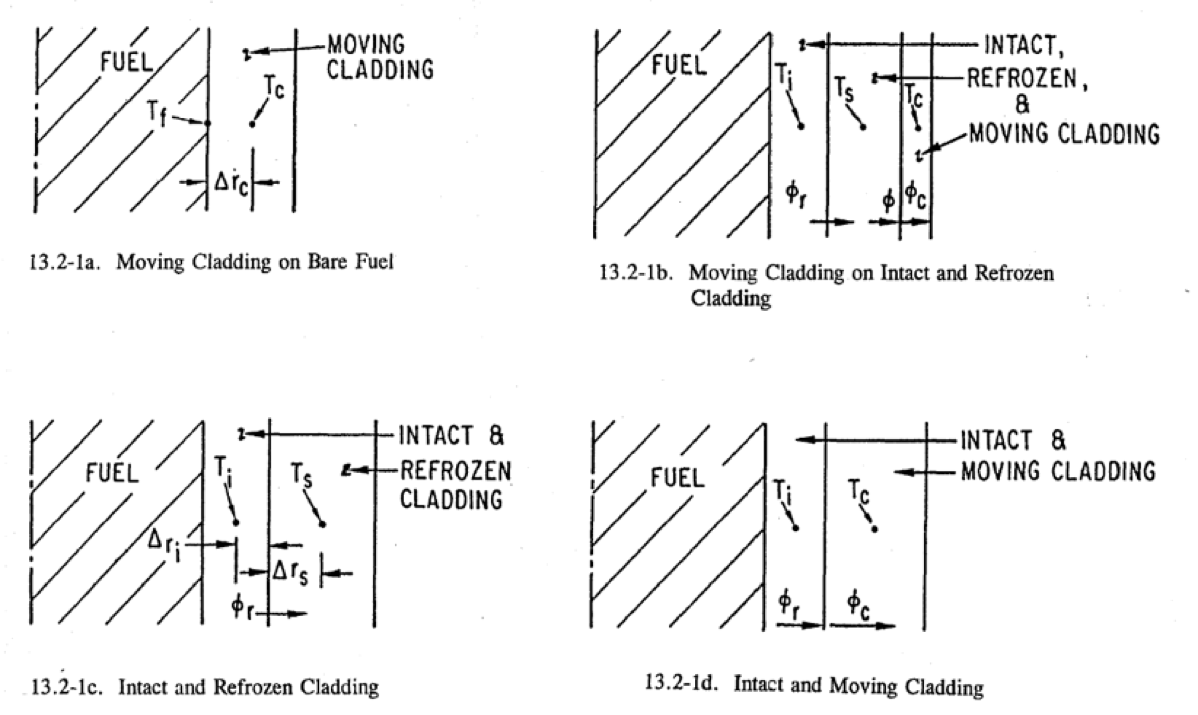
Figure 13.2.1 Schematic Showing the Different Heat-Transfer Configuration in CLAP

The same correlation and constants are used for computing heat-transfer coefficients for single-phase sodium flow in the channel, (Eq. (3.3-9) of Chapter 3). The correlation of Maresca and Dwyer [13-8] for in-line flow in rod bundles is recommended, for which the constants are:

(13.2-34)\[ C_{1} = 0.0155\left( \overline{\psi} \right)^{0.86}\]

(13.2-35)\[ C_{1} = 0.86\]

(13.2-36)\[ C_{3} = 6.66 + 3.126 \left( \frac{P}{D} \right) + 1.184 \left( \frac{P}{D} \right)^{2}\]

where \(\overline{\psi}\) = mean ratio of the thermal and momentum diffusivities, and \(\frac{P}{D}\) = rod pitch-to-diameter ratio. Since the code does not allow for flow-rate-dependent values for \(C_{1}\), it is suggested that \(\overline{\psi}\) be set equal to unity in Eq. (13.2-34) with the understanding that the resulting heat-transfer coefficients will be slightly overestimated.

13.2.4.2. Moving Cladding on Intact and Refrozen Cladding

Various configurations can exist in the region outside the molten zone, depending upon whether or not moving cladding and/or refrozen cladding are present in addition to the original intact solid cladding. In this subsection, we consider the case where all three components are present (see Figure 13.2.1). The various heat fluxes shown in the figure are given by

(13.2-37)\[ \phi_{\text{r}} = k_{\text{c}} \frac{\left( T_{\text{i}} - T_{\text{s}} \right)}{\left( \Delta r_{\text{i}} + \Delta r_{\text{s}} \right)}\]

(13.2-38)\[ \phi_{\text{r}} = k_{\text{c}} \frac{\left( T_{\text{s}} - T_{\text{m}} \right)}{\Delta r_{\text{s}}}\]

(13.2-39)\[ \phi_{\text{c}} = h \left( T_{\text{m}} - T_{\text{c}} \right)\]

where

\(T_{\text{i}}\) = temperature of the intact solid cladding

\(T_{\text{s}}\) = temperature of the refrozen cladding

\(T_{\text{m}}\) = cladding melting temperature

\(\Delta r_{\text{i}}\) = half-thickness of the intact solid cladding

\(\Delta r_{\text{s}}\) = half-thickness of the refrozen cladding.

The film coefficient formula is identical to Eq. (13.2-33) and the fusion heat flux \(\phi_{\text{hf}}\) is given by Eq. (13.2-29).

13.2.4.3. Intact and Refrozen Cladding

In the absence of moving cladding (see Figure 13.2.1), we set \(\phi = 0\) and \(\phi_{\text{hf}} = 0\). The heat transfer between the initial and refrozen cladding is computed from

(13.2-40)\[ \phi_{\text{r}} = k_{\text{c}} \frac{\left( T_{\text{i}} - T_{\text{s}} \right)}{\left( \Delta r_{\text{i}} + \Delta r_{\text{s}} \right)}\]

which is identical to Eq. (13.2-37).

13.2.4.4. Intact and Moving Cladding

The moving cladding may be sufficiently hot to melt through the layer of refrozen cladding; this results in the configuration (see Figure 13.2.1) in which just the intact cladding and moving cladding are present. In the numerical model this situation also arises when moving cladding first contacts the intact cladding in an axial segment, in which case refrozen cladding is formed and will be present in the next time step.

The heat fluxes \(\phi_{1}\) and \(\phi_{2}\) and trial heat flux are calculated as follows

(13.2-41)\[ \phi_{1} = k_{\text{c}} \left( T_{\text{i}} - T_{\text{m}} \right) \Delta r_{\text{i}}\]

(13.2-42)\[ \phi_{2} = h \left( T_{\text{m}} - T_{\text{c}} \right)\]

(13.2-43)\[ \phi_{\text{trial}} = \phi_{1} - \phi_{2}\]

Recalling that \(\phi_{\text{r}}\) is the outer surface heat flux for the initial cladding, \(\phi_{\text{c}}\) the sensible heat flux for moving cladding, and \(\phi_{\text{hf}}\) the latent heat flux associated with refrozen cladding, we have

(13.2-44)\[ \begin{aligned} \phi_{\text{hf}} = 0, \phi_{r} = \phi_{2}, \text{ and } \phi_{\text{c}} = \phi_{2} && \text{for }\phi_{\text{trial}} \geq 0 \end{aligned}\]

(13.2-45)\[ \begin{aligned} \phi_{\text{hf}} = \phi_{\text{trial}},\phi_{\text{r}} = \phi_{1}, \text{ and } \phi_{\text{c}} = \phi_{2} && \text{for } \phi_{\text{trial}} < 0 \end{aligned}\]

13.2.5. Cladding Physical Properties Relationships

The density of the solid and liquid cladding are assumed to be linear functions of temperature:

(13.2-46)\[ \rho_{\text{s}} = \rho_{\text{s}}^{0} \left\lbrack 1 - 3\beta \left( T - T_{\text{ref}} \right) \right\rbrack\]

(13.2-47)\[ \rho_{\text{c}} = \rho_{\text{c}}^{0} \left\lbrack 1 - C \left( T - T_{\text{m}} \right) \right\rbrack\]

where

\(\rho_{\text{s}}^{0}\) = density of solid cladding at reference temperature \(T_{\text{ref}}\)

\(\rho_{\text{c}}^{0}\) = density of cladding at the liquidus temperature

\(\beta\) = linear coefficient of thermal expansion for solid

\(C\) = volumetric coefficient of thermal expansion for liquid.

For partly-molten cladding, the density is evaluated using

(13.2-48)\[ \rho = \left\lbrack \frac{\left( 1 - f \right)}{\rho_{\text{s}}} \left( T_{\text{m}} \right) + \frac{f}{\rho_{\text{c}}} \right\rbrack^{- 1}\]

where \(f\) is the melt fraction as defined by Eq. (13.2-51).

The internal energies of the solid and molten cladding are also assumed to be linear functions of temperature

(13.2-49)\[ e_{\text{s}} = c_{\text{ps}} T\]

(13.2-50)\[ e_{\text{c}} = e_{\text{c}}^{o} + c_{\text{pc}} T\]

where \(e_{\text{c}}^{o} = \lambda^{o} + \left( C_{\text{ps}} - C_{\text{pc}} \right) T_{\text{m}}\), and math:lambda^{o} = heat of fusion. For mixtures, the mass melt fraction is given by

(13.2-51)\[ f = \frac{\left( e - c_{\text{ps}} T_{\text{m}} \right)}{\lambda^{o}}\]