3.10. Multiple-Pin Model

3.10.1. Introduction

The new multiple pin treatment was added to the code to account for pin-to-pin variations within a subassembly. This new multiple pin treatment can be used in at least two different ways. One approach is to use the new treatment to compute nominal or “best estimate” variations within a subassembly. Another approach is to compute hot channel behavior due to postulated deviations in coolant flow rate, coolant flow area, and pin power. When doing a whole-core analysis, one probably would not want the hot channel temperatures used in reactivity feedback calculation or in the core outlet temperatures that feed into the primary loop calculations. Therefore, one would probably use parallel treatments for the same subassembly: a nominal one-pin or multi-pin treatment used for reactivity feedback, plus a hot channel treatment decoupled from the reactivity feedback and from the primary loop calculation. The hot channel treatment would be de-coupled by setting reactivity feedback coefficients to zero and by setting the number of subassemblies represented by this treatment to zero.

The new multiple pin treatment allows a number of coupled channels to be used to model a single subassembly. Thus a channel can represent a part of a subassembly instead of the whole subassembly. Peaking factors can be mechanistically calculated by reducing coolant flow areas and flow rates or increasing pin power levels in some channels.

As previously mentioned, the multiple pin option is currently only available for steady-state and single phase transient calculations.

3.10.2. Physical Model

In the new multiple pin option, the regions above and below the pin section of a subassembly are still represented by a single channel; but a number of channels can be used to represent the pin section. Each channel in the pin section can represent one or more concentric rows of pins and their associated coolant. It is also possible for channels to represent slices of pins for a subassembly with a strong lateral power skew or for one with a hot subassembly on one side and a cool subassembly on the opposite side. Figure 3.10.1 illustrates one way that a number of channels can be used to model the pin section of a subassembly as concentric rings of pins and coolant subchannels. The thimble flow region in this figure is a feature of the EBR-II XX09 instrumented subassembly and is not found in ordinary subassemblies. This case concentrates on the coolant subchannels and splits the pins. It is also possible to shift the channel boundaries half a pin and use a pin-based representation with intact pins and split coolant subchannels. Currently up to 56 channels can be used to represent a subassembly.

The new option accounts for coolant-to-coolant heat transfer between adjacent channels, including the effects of both conduction and turbulent mixing. It also accounts for subassembly-to-subassembly heat transfer from the duct wall of a subassembly, through the interstitial sodium, to the duct wall of a neighboring subassembly. In addition, axial conduction in the coolant is accounted for.

Figure 3.10.2 illustrates the axial representation of the subassembly flow, with parallel flow paths through the pin section. Each channel used to represent the pin section of subassembly has its own separate time-dependent flow rate, and the flow rates in all channels in a subassembly are driven by common pressures at the inlet and outlet of the pin section. Thus, transient flow redistribution among channels is accounted for. The single flow rate in the regions above and below the pin section is the sum of the pin section flow rates, so the subassembly flow orifice sees the correct total flow rate. Even though the coolant-to-coolant heat transfer coefficient includes a term for turbulent mixing between coolant subchannels, one effect that the flow calculation does not account for is mass flow between channels in the pin section, although cross-flow at the ends of the pin section is allowed. Therefore, if recirculation loops occur within a subassembly at low flows, the model would calculate them; but the recirculation loops would go to the ends of the pin section.

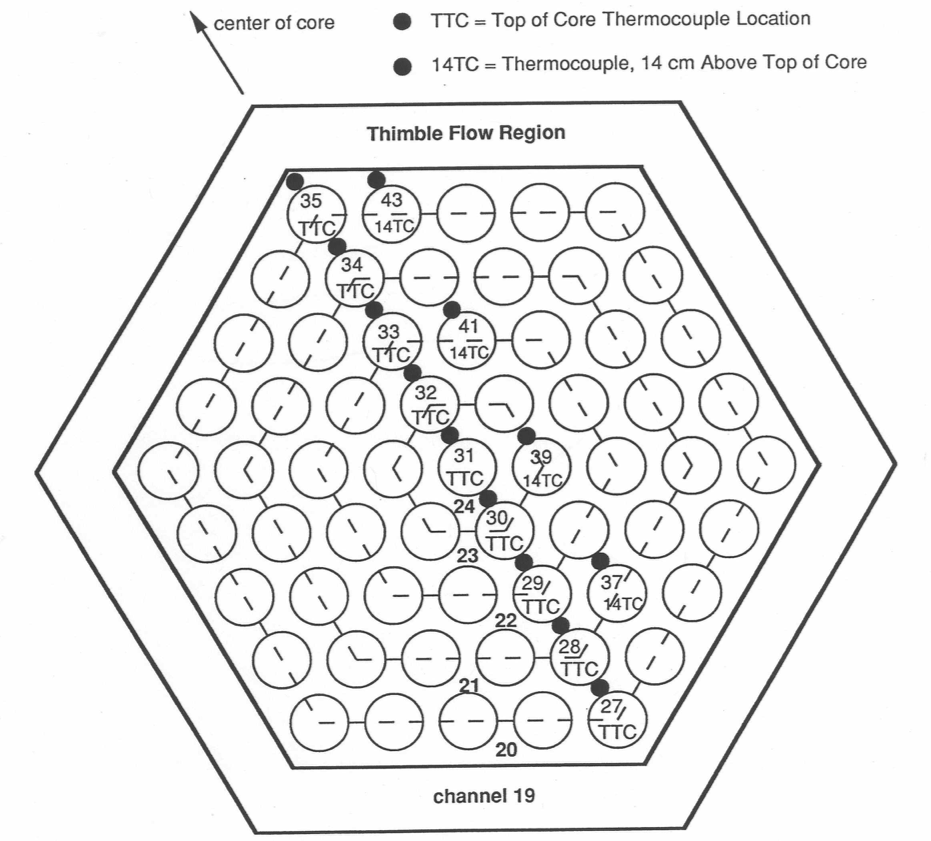
Figure 3.10.1 SAS4A/SASSYS‑1 Multiple Pin Representation and Thermocouple Locations for the EBR-II XX09 Instrumented Subassembly

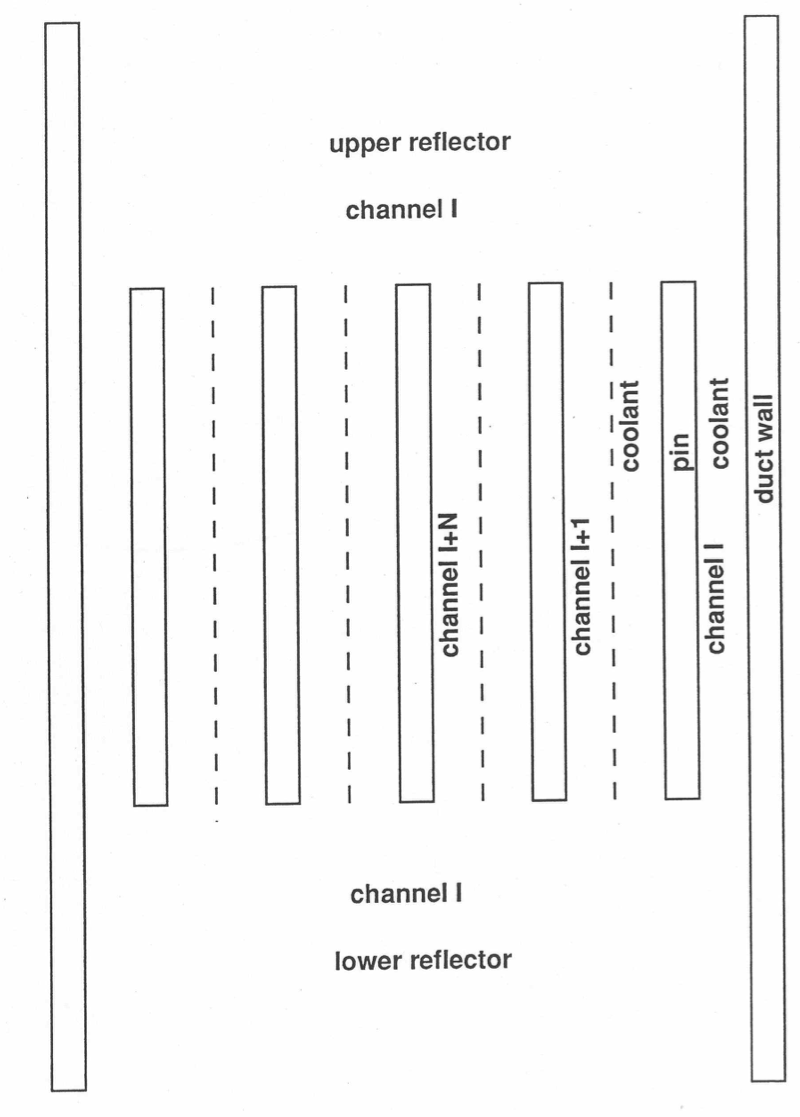
Figure 3.10.2 SAS4A/SASSYS‑1 Multiple Pin Treatment of a Subassembly

In the new model the coolant in channel I can transfer heat directly to the coolant in channel \(\text{I}-1\) and channel \(\text{I}+1\). Using correlations of the same form as those used in THI3D code [3-6] and the HOTCHAN code [3-7], the channel-to-channel heat flow per pin per unit height from channel I to channel \(\text{I}+1\) is calculated as:

(3.10‑1)

\[Q_{\text{I,I} + 1} = \left\lbrack U_{1}\overline{k} + U_{2} \overline{C}\left( w_{1} + w_{\text{I} + 1} \right) \right\rbrack \left( T_{\text{I}} - T_{\text{I} + 1} \right)\]

where

\(\overline{k}\) = average thermal conductivity of the coolant

\(\overline{C}\) = average specific heat

\(w_{\text{i}}\) = coolant mass flow per pin (kg/s) in channel \(I\),

and

\(T_{\text{I}}\) = coolant temperature

In this equation, \(U_{\text{I}}\) is a geometry factor for thermal conduction, and \(U_2\) is a product of a turbulent-mixing coefficient and a geometry factor for turbulent mixing between channels. Since a SAS4A/SASSYS‑1 channel usually models a group of coolant subchannels, the values used for \(U_1\) and \(U_2\) must account for a combination of parallel and series heat flow paths between the middle of channel \(I\) and the middle of channel \(I + 1\). Subassembly-to-subassembly heat transfer is handled in a somewhat simpler manner. For heat transfer from the outer surface of the structure in channel \(I\) to the outer surface of the structure in channel \(J\), a constant value is used for the produce of the heat transfer coefficient and the heat transfer area per unit height.

3.10.3. Numerical Methods

Most of the transient heat transfer calculations and flow rate calculations in SASSYS-1 use semi-implicit time differencing in order to obtain stable and accurate solutions with reasonably long time steps. Before the onset of coolant boiling or pin disruption, time step sizes of a second or more are commonly used; and the code usually runs significantly faster than real time on a Cray XMP computer.

From a numerical computation point of view, the two main tasks in adding the multiple pin model to the code were the coolant-to-coolant heat transfer calculation and the coolant flow rate calculation with parallel flow paths in the pin section. Both of these calculations use semi-implicit time differencing. In the single-pin model, coolant temperatures for all of the radial temperature nodes in the pin, coolant, and structure at one axial node are solved for simultaneously in order to obtain a semi-implicit time differencing solution without iteration. In the new multiple-pin treatment, this concept is carried one step further. At a given axial node, temperature at all of the radial nodes for all channels representing a subassembly are solved for simultaneously. In the heat transfer calculations, the axial conduction terms, which are small, are treated with explicit forward time differencing so that axial nodes are decoupled and can be treated separately except for the coolant convection terms. The axial coupling due to the coolant convection terms is handled by starting at one end of the subassembly and solving for axial nodes one at a time in the direction of the flow. If flow has reversed in some channels but not in others, the calculation progresses in the direction of the dominate flow; and explicit forward differencing is used for the coolant convection terms in the non-dominate flow direction channels. The subassembly-to-subassembly heat fluxes are calculated with explicit forward differencing in time, and this does impose a stability limit on the time step size. For typical subassembly duct wall thicknesses, the explicit subassembly-to-subassembly heat flux calculation limits the maximum time step size to a value in the range from .25 to .5 seconds. For the coolant flow rate calculations, the incompressible flow momentum equations are linearized about conditions at the beginning of the time step. Then, flow at the end of the step are calculated for all channels in a subassembly simultaneously.

A null transient is used to obtain steady-state temperatures at the start of the regular transient. First all coolant, pin, structure, and reflector temperatures in all subassemblies are set to the coolant inlet temperature. Then, the power levels and coolant flow rates are held constant while a number of transient heat transfer time steps are made. Since the pin thermal time constant and the coolant transit time through a subassembly are both less than a second, the null transient results converge rapidly if reasonably large time steps are used.

3.10.4. Detailed Mathematical Treatment

The main computational parts of the new multiple pin model are the heat transfer calculations in the pin section of a subassembly, the coolant flow rate calculations for a subassembly, the subassembly-to-subassembly heat transfer, and changes to the driver routines to call the appropriate new routines at the proper times. The pin section heat transfer calculations are done in two new subroutines: TSHTM3 calculates temperatures in the core and axial blankets, and TSHTM2 calculates temperatures in the gas plenum region. The existing TSHTN1 still calculates temperatures in the reflector zones above and below the pin section, but it was modified. TSHTN1 had to be modified slightly to pick up mixed mean outlet temperatures from the multiple channels representing the pin section. Also, axial conduction in the coolant was added to TSHTN1. The new TSCLM1 routine calculates transient coolant flow rates for a subassembly. The subassembly-to-subassembly heat fluxes are calculated in CHCHFL.

3.10.4.1. Heat Transfer Calculations in the Core and Axial Blankets: Subroutine TSHTM3

The multiple pin heat transfer calculations for the core and axial blankets in subroutine TSHTM3 are similar to the single pin calculations in the existing subroutine TSHTN3, as described in Section 3.3.1. One difference is that TSHTN3 does one time step for one channel each time it is called, whereas TSHTM3 solves for temperatures in all pins or channels representing a subassembly when it is called. Also, TSHTM3 adds extra terms for coolant-to-coolant heat transfer; and TSHTM3 includes axial conduction in the coolant.

Within a fuel pin, one-dimensional radial heat transfer is used. The basic heat transfer equation is Eq. 3.3-1. This part of the calculation in TSHTM3 is identical to the corresponding calculation in TSHTN3.

For the coolant in channel I, the heat transfer calculations are basically one-dimensional in the axial direction, with extra terms for coolant-to-coolant heat transfer from channel \(I-1\) and \(I+1\). The basic heat transfer equation is:

(3.10‑2)

\[\rho c A_{\text{c}}\frac{\partial \text{T}}{\partial \text{t}} + \frac{\partial}{\partial \text{z}}\left( wcT \right) = Q_{\text{T}}A_{\text{c}}\]

where

\(A_{\text{c}}\) = coolant flow area

\(z\) = axial position

\(w\) = coolant mass flow rate

and

\(Q_{\text{r}}\) = total heat source per unit volume

The heat source contains a number of terms:

(3.10‑3)

\[Q_{\text{T}} = Q_{\text{c}} + Q_{\text{ec}} + Q_{\text{sc}} + Q_{\text{ax}} + {Q'}_{\text{I} - 1,\text{I}} - {Q'}_{\text{I,I} + 1}\]

where

\(Q_{\text{c}}\) = source due to direct heating of the coolant by neutrons and gamma rays,

\(Q_{\text{ec}}\) = heat flow from cladding to coolant,

\(Q_{\text{sc}}\) = heat flow from structure to coolant,

\(Q_{\text{ax}}\) = axial conduction source, given by

(3.10‑4)

\[Q_{\text{ax}} = \frac{\partial}{\partial \text{z}} k \frac{\partial \text{T}}{\partial \text{z}}\]

and

(3.10‑5)

\[{Q'}_{\text{I,I} + 1} = \frac{Q_{\text{I,I} + 1}}{A_{\text{c}}}\]

where \({Q'}_{\text{I,I} + 1}\) is given by equation 3.10-1. Note that Eq. 3.10-2 is the same as Eq. 3.3-5, except that additional source terms are included in the multiple pin model.

Finite differencing in space and time is used to solve these heat transfer equations. Figure 3.2.3 shows the axial and radial mesh used for a single channel. In the multiple pin model the pin section mesh is repeated for each channel, but the axial reflector zones are only used in the first channel used to represent a subassembly. At each axial node in the core and axial blankets a number of radial nodes are used for the fuel, three radial nodes are used for the cladding, one node is used in the coolant, and two nodes are used in the structure. All channels, representing a subassembly must use the same axial mesh. Also, all subassemblies connected by subassembly-to-subassembly heat transfer must use the same axial mesh.

For a given time step, Eqs. 3.3-1 and 3.10-2 become linear finite difference equations. The temperatures are known at the beginning of the time step, and the temperature at the end of the step are the unknowns to be solved for. Semi-implicit time differencing is used for all terms except the axial conduction terms \(Q_{\text{ax}}\), and the coolant-to-coolant terms \(Q_{\text{I} - 1,\text{I}}\) and \({Q'}_{\text{I,I} + 1}\). The \(Q_{\text{ax}}\) axial conduction term is calculated explicitly based on temperatures at the beginning of the time step. The coolant-to-coolant terms are calculated fully implicitly, using the coolant flow rates and temperatures at the end of the step.

After finite differencing for one axial node, one obtains N simultaneous liner equations in N unknowns, where the unknowns are the temperatures at the end of the time step for all radial nodes in all channels representing the subassembly. These equations are solved by Gaussian elimination. The equations are basically tri-diagonal, with extra non-tri-diagonal terms for coolant-to-coolant heat transfer between channels. No full N by N matrix is ever set up by TSHTM3, and a general full matrix solution package is not used. Instead, only non-zero terms are computed and stored; and the Gaussian elimination solution was written specifically for this set of equations. The result is that the storage requirements vary linearly, rather than quadratically, with the maximum allowable value for N; and the computation time varies linearly, rather than quadratically, with the actual value of N.

3.10.4.2. Heat Transfer Calculations in the Gas Plenum Region: Subroutine TSHTM2

Subroutine TSHTM2 does the heat transfer calculations for one time step for all axial nodes in the gas plenum region for all channels representing a subassembly when it is called. TSHTM2 is similar to TSHTM3, but TSHTM2 deals with fewer radial nodes. As shown in Figure 3.2.5, in the plenum region there are still two radial nodes in the structure and one in the coolant; but there is only one in the cladding; and there are no fuel nodes. Instead of fuel temperatures there is one gas temperature common to all of the axial nodes in a pin. As in TSHTM3, for a given axial node TSHTM2 solves simultaneously for temperatures at all radial modes in all channels representing a subassembly.

One special problem in TSHTM2 is the gas temperature, which is common to all axial nodes in the gas plenum region of a pin. Axial nodes are handled one at a time, rather than simultaneously, whereas a semi-implicit time differencing treatment would require solving for all axial nodes simultaneously. The new multiple-pin TSHTM2 routine handles this problem in a simpler manner than the old single-pin TSHTN2. The way that the gas temperature is handled is TSHTM2 is to calculate a separate gas temperature for each axial node. At the beginning of the time step, the gas temperatures at all axial nodes are set to one common value. Then separate values are calculated for each axial node at the end of the step. Finally, an average of the separate values is calculated for the one common value at the ed of the step.

3.10.4.3. Coolant Flow Rates: Subassembly TSCLM1

The coolant for rate calculation for a subassembly in the multiple-pin routine TSCLM1 is much more complex than the corresponding calculation in the single pin routine TSCNV1. As shown in Figure 3.10.2, the multiple pin calculation involves multiple parallel flow paths in the pin section, in series with single flow paths in the reflector regions. Therefore, the multiple-pin routine TSCLM1 was written from scratch, rather than starting form the single pin TSCNV1 routine.

Figure 3.10.3 illustrates the main variables used in TSCLM1.

Incompressible flow is used for these calculations, so conservation of mass gives

(3.10‑6)

\[N_{1}\ w_{\text{r}} = \sum_{\text{k}}{w_{\text{pk}} N_{\text{k}}}\]

where

\(w_{\text{r}}\) = coolant mass flow rate per pin in the reflector zones,

\(w_{\text{pk}}\) = pin section coolant mass flow rate per pin in channel k,

\(N_{\text{k}}\) = number of pins in channel k,

and

\(I\) = channel number of the first channel representing the subassembly.

The momentum equation for the pin section is

(3.10‑7)

\[\frac{L_{\text{p}}}{A_{\text{cpk}}} \frac{d\text{w}_{\text{pk}}}{\text{dt}} = p_{\text{b}} - p_{\text{c}} - \Delta p_{\text{pk}}\]

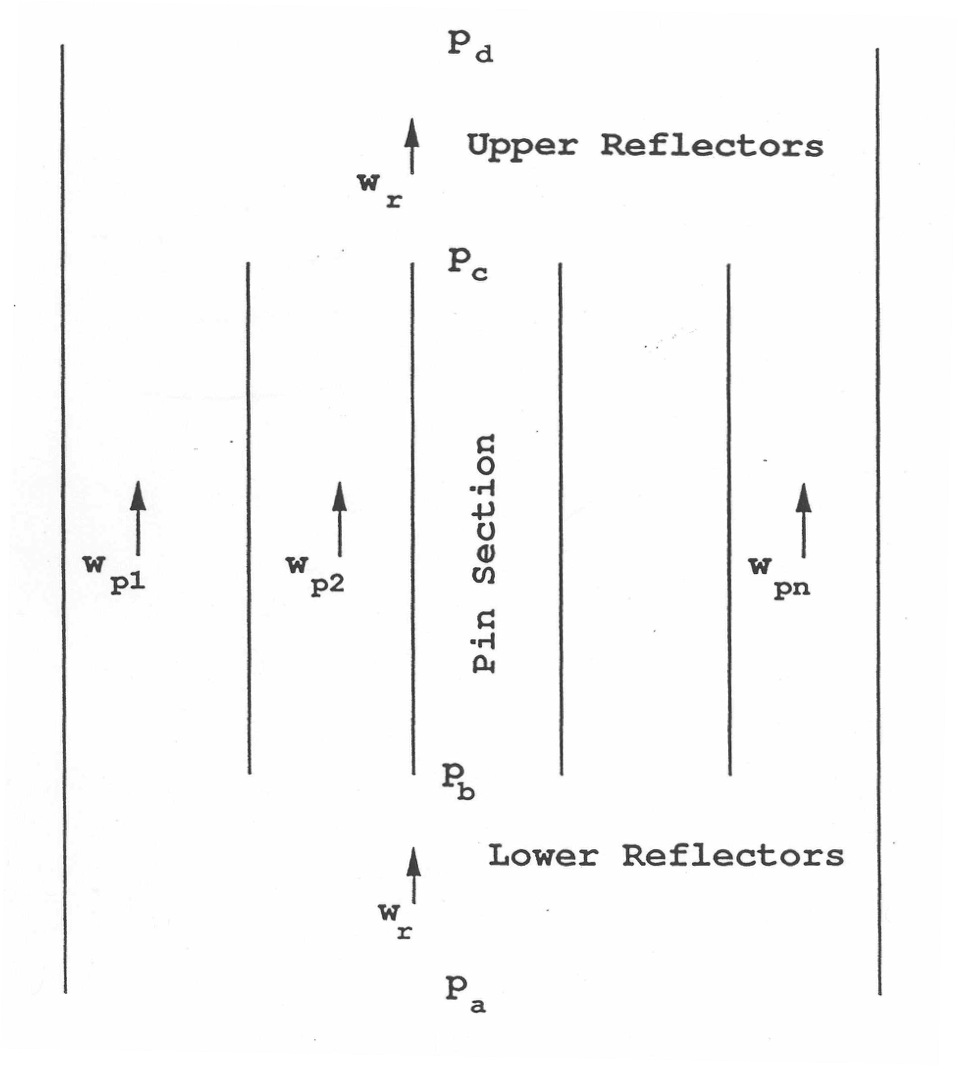
Figure 3.10.3 Subassembly Coolant Flows

where

\(L_{\text{p}}\) = length of pins,

\(A_{\text{cpk}}\) = coolant flow area in channel k in the pin section,

\(t\) = time,

\(p_{\text{b}}\) = coolant pressure at the bottom of the pins,

\(p_{\text{c}}\) = coolant pressure at the top of the pins,

(3.10‑8)

\[\Delta p_{\text{pk}} = \text{ pressure loss } = \sum_{\text{jv} = \text{JCPNBT}}^{\text{JCPNTM}}{\Delta p_{\text{kjc}}}\]

\(jc\) = axial coolant node,

\(\text{JCPNBT}\) = first axial node in the pin section

\(\text{JCPNTM}\) = last axial node in the pin section,

and

\(\Delta p_{\text{kjc}}\) = pressure loss in axial node jc of channel \(k\).

The pressure loss contains a number of terms:

(3.10‑9)

\[\Delta p_{\text{kjc}} = \Delta p_{\text{frkjc}} + \Delta p_{\text{grkjc}} + \Delta p_{\text{orkjc}} + \Delta p_{\text{acckjc}}\]

where

(3.10‑10)

\[\Delta p_{\text{frkjc}} = \text{ friction loss } = \frac{f_{\text{kjc}}\Delta z_{\text{jc}}w_{\text{pk}}\left| w_{\text{pk}} \right|}{2{\overline{\rho}}_{\text{ckjc}}\ A_{\text{cpk}}\ D_{\text{hpk}}}\]

(3.10‑11)

\[\Delta p_{\text{grpjc}} = \text{ gravity head } = g {\overline{p}}_{\text{ckjc}} \Delta z_{\text{jc}}\]

(3.10‑12)

\[\Delta p_{\text{orfkjc}} = \text{ orifice loss } = \frac{K_{\text{orkjc}} w_{\text{pk}} \left| w_{\text{ph}} \right|}{2{\overline{\rho}}_{\text{ckjc}}A_{\text{cpk}}^{2}}\]

(3.10‑13)

\[\Delta p_{\text{acckjc}} = \text{ acceleration term } = \frac{w_{\text{pk}}^{2}}{A_{\text{cpm}}^{2}}\left( \frac{1}{\rho_{\text{ckjc} + 1}} - \frac{1}{\rho_{\text{ckjc}}} \right)\]

\(\Delta z_{jc}\) = axial node length,

\(f_{\text{kjc}}\) = friction factor in channel k at node \(jc\),

\(\rho_{\text{ckjc}}\) = coolant density at bottom of node \(jc\) in channel \(k\),

\({\overline{\rho}}_{\text{ckjc}}\) = average coolant density in node \(jc\) in channel \(k\),

\(D_{\text{hpk}}\) = Hydraulic diameter,

and

\(K_{\text{orkjc}}\) = orifice coefficient in node \(jc\) of channel \(k\)

The friction factor is calculated as in Eq. (3.9-4).

using

(3.10‑14)

\[\text{Re}= \text{ Reynolds number } = \frac{D_{\text{hpk}}\left| w_{\text{pk}} \right|}{\mu_{\text{kjc}}\ A_{\text{cpk}}}\]

and

\(\mu_{\text{kjc}}\) = viscosity of the coolant.

After semi-implicit finite differencing in time and linearization of the pressure drop terms, applying Eq. 3.10-7 to a time step from \(t\) to \(t + \Delta t\) gives

(3.10‑15)

\[\frac{L_{\text{p}}}{A_{\text{cpk}}} \frac{\Delta w_{\text{pk}}}{ \Delta t } = p_{\text{b}}\left( t \right) + \theta_{2}\Delta p_{\text{b}} - p_{\text{c}}\left( t \right) - \theta_{2}\Delta p_{\text{c}} - \Delta p_{\text{pk}}\left( t \right) - \theta_{2} \Delta w_{\text{pk}}K_{\text{wpk}}\]

where

(3.10‑16)

\[\Delta w_{\text{pk}} = w_{\text{pk}}\left( t + \Delta t \right) - w_{\text{pk}}\left( t \right)\]

(3.10‑17)

\[\Delta p_{\text{b}} = p_{\text{b}}\left( t + \Delta t \right) - p_{\text{b}}\left( t \right)\]

(3.10‑18)

\[\Delta p_{\text{c}} = p_{\text{c}}\left( t + \Delta t \right) - p_{\text{c}}\left( t \right)\]

\(\theta_{2}\) = degree of implicitness

(3.10‑19)

\[\theta_{1} = 1 - \theta_{2}\]

(3.10‑20)

\[K_{\text{wpk}} = \sum_{\text{jc} = \text{JCPNBT}}^{\text{JCPNTM}}{K_{\text{wpkjc}}}\]

(3.10‑21)

\[K_{\text{wpkjc}} = \frac{\partial\Delta \text{p}_{\text{kjc}}}{\partial \text{w}_{\text{pk}}} = K_{\text{frkjc}} + K_{\text{wcrkjc}} + K_{\text{acckjc}}\]

(3.10‑22a)

\[\begin{split}K_{\text{frkjc}} = \begin{cases} \left( 2 + b_{\text{fr}} \right)\frac{\Delta p_{\text{frkjc}}\left( t \right)}{w_{\text{pk}}\left( t \right)} & \text{if }R_{\text{ckjc}}\ \geq \ R_{\text{et}} \\ \frac{\Delta p_{\text{frkjc}}\left( t \right)}{w_{\text{pk}}\left( t \right)} & \text{if }R_{\text{ckjc}}\ < \ R_{\text{et}} \\ \end{cases}\end{split}\]

or

(3.10‑22b)

\[K_{\text{frkjc}} = \left\lbrack \left( 2 + b_{\text{fr}} \right)A_{\text{fr}} A \left( \text{RE} \right)^{b_{\text{fr}}} + \frac{A_{\text{fL}}}{\text{RE}} \right\rbrack\frac{\Delta z_{\text{jc}}\left| w_{\text{pk}}\left( t \right) \right|}{2p_{\text{ckjc}}D_{\text{hpk}}A_{\text{cpk}}}\]

(3.10‑23)

\[K_{\text{wpkjc}} = \frac{2\Delta p_{\text{orfkjc}}\left( t \right)}{w_{\text{pk}}\left( t \right)}\]

and

(3.10‑24)

\[k_{\text{acckjc}} = \frac{2\Delta p_{\text{acckjc}}\left( t \right)}{w_{\text{pk}}\left( t \right)}\]

Equation 3.10-15 can then be written as

(3.10‑25)

\[\Delta p_{\text{b}} - \Delta p_{\text{c}} = d_{0\text{pk}} + d_{0\text{pk}} + d_{1\text{pk}}\Delta w_{\text{pk}}\]

where

(3.10‑26)

\[d_{0\text{pk}} = \frac{p_{\text{c}}\left( t \right) - p_{\text{b}}\left( t \right) + \Delta p_{\text{pk}}\left( t \right)}{\theta_{2}}\]

and

(3.10‑27)

\[d_{1\text{pk}} = \frac{\frac{L_{\text{p}}}{A_{\text{cpk}}} + \theta_{2} \Delta t K_{\text{wpk}}}{\theta_{2} \Delta t }\]

Applying a similar process to the upper and lower reflector regions gives:

(3.10‑28)

\[\Delta p_{\text{b}} = D_{0\text{l}} + D_{1\text{l}} \sum_{\text{k}} \Delta w_{\text{pk}}\]

and

(3.10‑29)

\[\Delta p_{\text{c}} = D_{0\text{u}} + D_{1\text{u}} \sum_{\text{k}} \Delta w_{\text{pk}}\]

where

(3.10‑30)

\[D_{0\text{l}} = \frac{\theta_{1}p_{\text{a}}\left( t \right) + \theta_{2} p_{\text{a}}\left( t + \Delta t \right) - p_{\text{b}}\left( t \right) - \Delta p_{\text{l}}\left( t \right)}{\theta_{2}}\]

(3.10‑31)

\[D_{1\text{l}} = \frac{- \sum_{\text{KA} = 1}^{\text{KZPIN} - 1}{\frac{L_{\text{kz}}}{A_{\text{cKZ}}}} - \theta_{2} \Delta t K_{w\text{l}}}{\theta_{2} \Delta t }\]

(3.10‑32)

\[D_{0\text{u}} = \frac{\theta_{1}p_{\text{d}}\left( t \right) + \theta_{2}\ p_{\text{d}}\left( t + \Delta t \right) - p_{\text{c}}\left( t \right) + \Delta p_{\text{u}}\left( t \right)}{\theta_{2}}\]

(3.10‑33)

\[D_{1\text{u}} = \frac{\sum_{\text{KZ} - \text{KZPIN} + 1}^{\text{KZM}}{\frac{\text{L}_{\text{KZ}}}{A_{\text{cKZ}}}} + \theta_{2} \Delta t K_{\text{wu}}}{\theta_{2} \Delta t }\]

\(L_{\text{KZ}}\) = length of zone \(kz\)

\(A_{\text{cKZ}}\) = coolant flow area in zone \(kz\)

\(\text{KZPIN}\) = axial zone number of the pin section

\(\text{KZM}\) = last zone number

(3.10‑34)

\[\Delta p_{\text{l}} = \sum_{\text{jc} = 1}^{\text{JCPNBT} - 1}{ \Delta p_{\text{rjc}}}\]

(3.10‑35)

\[\Delta p_{\text{u}} = \sum_{\text{jc} = \text{JCPNTP}}^{\text{MZCM}1} \Delta p_{\text{rjc}}\]

\(\Delta p_{\text{rjc}}\) = pressure loss in node \(jc\) of a reflector zone

\(\text{JCPNBT}\) = first axial node in pin section

\(\text{JCPNTP}\) = first axial node above the pin section

\(\text{MZCM}1\) = last axial node

(3.10‑36)

\[K_{\text{wl}} = \frac{\partial\Delta p_{\text{l}}}{\partial w_{\text{r}}}\]

and

(3.10‑37)

\[K_{\text{wu}} = \frac{\partial\Delta p_{\text{u}}}{\partial w_{\text{u}}}\]

Then, combining Eqs. (3.10-25) and (3.10-28) gives

(3.10‑38)

\[\Delta p_{\text{b}} = B_{\text{o}} + B_{1} \Delta p_{\text{c}}\]

where

(3.10‑39)

\[B_{\text{o}} = \frac{D_{\text{ol}} - D_{1\text{l}} S_{1}}{1 - D_{1\text{f}} S_{\text{o}}}~,\]

(3.10‑40)

\[B_{1} = \frac{- D_{1\text{l}}S_{\text{o}}}{1 - D_{1\text{l}}S_{\text{o}}}\]

(3.10‑41)

\[S_{\text{o}} = \sum_{\text{k}}{ \frac{1}{d_{1\text{pk}}}}~ ,\]

and

(3.10‑42)

\[S_{1} = \sum_{\text{k}}{ \frac{d_{\text{opk}}}{d_{1\text{pk}}}}~ ,\]

Similarly, combining Eqs. (3.10-25) and (3.10-29) gives

(3.10‑43)

\[\Delta p_{\text{c}} = C_{\text{o}} + C_{1} \Delta p_{\text{b}}\]

where

(3.10‑44)

\[C_{\text{o}} = \frac{D_{\text{ou}} - D_{1\text{u}} S_{1}}{1 + D_{1\text{u}} S_{\text{o}}}~ ,\]

and

(3.10‑45)

\[C_{1} = \frac{D_{1\text{u}} S_{\text{o}}}{1 + D_{1\text{u}} S_{\text{o}}}~ .\]

Combining Eqs. (3.10-38) and (3.10-43) gives

(3.10‑46)

\[\Delta p_{\text{c}} = \frac{C_{\text{o}} + C_{1}B_{\text{o}}}{1 - C_{1} B_{1}}\]

Then \(\Delta p_{\text{b}}\) can be obtained from Eq. (3.10-38) and \(\Delta w_{\text{bk}}\) can be obtained from Eq. (3.10-25) for each channel.

After \(p_{\text{b}}\), \(p_{\text{c}}\), and the coolant flow rates have been calculated for the end of the time step it is possible to calculate the pressures. The pressure is calculated at the axial node boundaries. \(p_{\text{kjc}}\) is the pressure at the bottom (inlet end) of node \(jc\) in channel \(k\). First, the nodal pressure loss at \(t + \Delta t\) is calculated as

(3.10‑47)

\[\Delta p_{\text{pkjc}}\left( t + \Delta t \right) = \Delta p_{\text{kjc}}\left( t \right) + K_{\text{wpkjc}} \Delta w_{\text{pk}}\]

and \(\Delta p_{\text{pk}} (t + \Delta t)\) is calculated from Eq. (3.10-8). Then Eq. (3.10-7) is used to obtain \(\frac{\text{dw}_{\text{pk}}\left( t + \Delta t \right)}{\text{dt}}\).

Integrating the momentum equation over one axial node gives

(3.10‑48)

\[\frac{\Delta z_{\text{j}}}{A_{\text{cpk}}} \frac{\text{dw}_{\text{pk}}}{\text{dt}} = p_{\text{pkjc}} - p_{\text{pkjc} + 1} - \Delta p_{\text{kjc}}\]

Starting by setting

(3.10‑49)

\[p_{\text{pkjJCPNTP}} = P_{\text{c}}\]

the code marches down the channel, using Eq. (3.10-48) to obtain \(p_{\text{pkjc}}\) after \(p_{\text{pkjc}+1}\) has been calculated. A similar procedure is used for calculating the pressures in the upper and lower reflector zones.

The equation used to compute the degree of implicitness as a function of time step size in TSCMV1 is

(3.10‑50)

\[\theta_{2} = \frac{a + bx + x^{2}}{2a + cx + x^{2}}\]

where

(3.10‑51)

\[x=\Delta t/\tau\]

\(\tau\) = a time constant

\(a\) = 6.12992

\(b\) = 2.66054

and

\(c\) = 3.56284

The basis for this expression is given in Section 3.19.1. For a single channel treatment, the time constant, \(\tau\) would be

(3.10‑52)

\[\tau = \frac{\sum_{\text{KZ} = 1}^{\text{KZM}}{ \frac{L_{\text{KZ}}}{A_{\text{cKZ}}} + \left( \frac{L_{\text{i}}}{A} \right)_{\text{i}} + \left( \frac{L_{\text{i}}}{A} \right)_{\text{x}}}}{K_{\text{wpk}}\ K_{\text{w}1} + K_{\text{wu}}}\]

where

\(\left( \frac{L_{\text{i}}}{A} \right)_{\text{i}}\) = extra coolant inertia term at the subassembly inlet to account for inertia of the coolant in the inlet plenum,

and

\(\left( \frac{L_{\text{i}}}{A} \right)_{\text{x}}\) = same for the subassembly outlet.

Since a simultaneous solution of flows in all channels of an assembly plus the lower and upper reflector zones is required, the overall time constant is calculated as

(3.10‑53)

\[\tau = \frac{ \frac{L_{\text{p}}}{\sum_{\text{k}}{A_{\text{cpk}}}} + \sum_{\text{kZ} \neq \text{KZPIN}}{\frac{L_{\text{KZ}}}{A_{\text{cKZ}}} + \left( \frac{L_{\text{i}}}{A} \right)_{\text{i}} + \left( \frac{L_{\text{i}}}{A} \right)_{\text{x}}} }{K_{\text{w}1} + K_{\text{wu}} + \frac{1}{\sum_{k}{\frac{1}{k_{\text{wpk}}}}}}\]

3.10.5. Relationship Between Single Pin and Multiple Pin Models

The single pin treatment and the multiple pin treatment coexist in the SAS4A/SASSYS‑1 code; it is possible to use single pin treatments for some subassemblies and multiple pin treatments for other subassemblies in the same problem. There are now two separate sets of subroutines in the code for computing single phase thermal hydraulics: the single pin routines and multiple pin routines. Since the multiple pin model can handle the case of a single pin per subassembly, the single pin single phase thermal hydraulics subroutines are now redundant; and at some point in the future they will probably be removed from the code.

As previously mentioned, currently the multiple pin model is only available for steady state and single phase transient calculations; no multiple pin treatment is available in the code for coolant boiling, pin disruption, or relocation of fuel or cladding. In the future, the multiple pin treatment will probably be extended to coolant boiling and to relocation of fuel and cladding.