3.14. Subchannel Treatment Details

Argonne and the Korea Atomic Energy Research Institute (KAERI) cooperated on an International Nuclear Energy Research Initiative on “Passive Safety Optimization in Liquid Sodium-Cooled Reactors.” Part of this work involved the development, implementation, and testing of a detailed whole core coolant subchannel model for inclusion in the Argonne SAS4A/SASSYS‑1 LMR safety analysis code and the KAERI SSC-K systems code [3-8]. The purpose of this work was to increase the accuracy and decrease the uncertainties in calculations of reactor safety margins in accident situations. Steady-state and transient hot channel factors are computed mechanistically with a detailed subchannel model for the core, coupled with a thermal hydraulic treatment of the primary and intermediate heat transport loops. It should be noted here that some of the notation used in this section does not match that used in the preceding sections of this chapter. Therefore, all variables are defined in order to avoid confusion.

3.14.1. Model Features

The new model uses a coolant subchannel treatment similar to that used by the COBRA-4 code [3-9] or the SUPERENERGY-2 code [3-10]. The subchannel treatment includes axial coolant flow parallel to the pins and cross flow between coolant subchannels driven by pressure differences and wire wrap sweeping. Heat flow between adjacent coolant subchannels is calculated, including effects of turbulent mixing. The channel treatment includes the whole length of the subassembly, with the detailed subchannel treatment in the pin section and a simpler treatment above and below the pins.

Figure 3.14.1 shows a typical subchannel treatment for fuel pins with a triangular arrangement in a hexagonal duct. In this arrangement, there are interior subchannels, edge subchannels and corner subchannels. If the pins are wrapped with spacer wires, then there would be wire wrap flow sweeping along the duct walls in the edge and corner subchannels. This is the type of geometry the model is intended for, but the geometry is not hard-wired into the code. The model is flexible enough to model other geometries, such as pins in a square arrangement with grid spacers and no wire wraps. The new model couples with existing models for the remainder of the primary loop, intermediate loop and balance of plant.

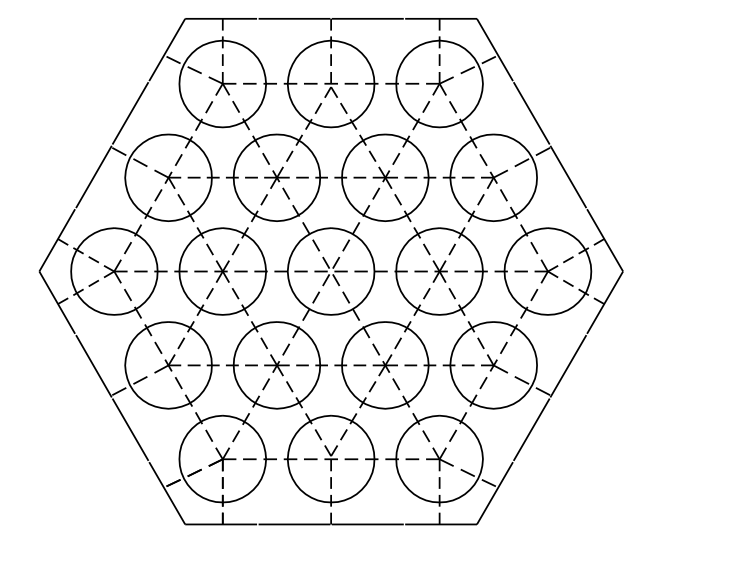
Figure 3.14.1 Coolant Subchannels in a 19 Pin Hex

3.14.2. Basic Equations

Figure 3.14.2 shows the main coolant subchannel variables used in the model for an axial node.

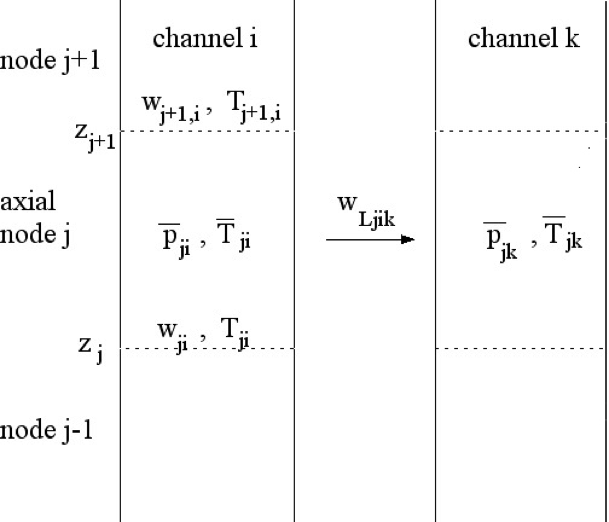
Figure 3.14.2 Coolant Subchannel Variables

The coolant variables in Figure 3.14.2 are defined as:

\({\overline{p}}_{\text{ji}}\) = coolant pressure at the middle of node j in channel i

\({\overline{T}}_{\text{ji}}\) = average coolant temperature for node j in channel i

\(w_{\text{ji}}\) = coolant flow rate in the axial direction at the bottom of node j in sub- channel i

\(w_{\text{Ljik}}\) = lateral flow rate from subchannel i to subchannel k at node j

\(z_{\text{j}}\) = axial location at the bottom of node j

The basic continuity equation for the coolant in an axial node of a subchannel is

(3.14-1)

\[\frac{\text{d}}{\text{dt}}({\overline{\rho}}_{\text{ji}}A_{\text{ji}}\Delta z_{\text{j}}) = w_{\text{ji}} - w_{\text{j} + 1,\text{i}} - \sum_{\text{k}}w_{\text{Ljik}}\]

The coolant momentum equation is

(3.14-2)

\[\begin{split}\begin{matrix} \frac{1}{2}(\frac{\Delta z_{\text{j}}}{A_{\text{ji}}} + \frac{\Delta z_{\text{j} - 1}}{A_{\text{j} - 1,\text{i}}})\frac{\text{dw}_{\text{ji}}}{\text{dt}} = {\overline{p}}_{\text{j} - 1,\text{i}} - {\overline{p}}_{\text{ji}} - \Delta p_{\text{frji}} - \frac{w_{\text{ji}}|w_{\text{ji}}|K_{\text{orji}}}{2\rho_{\text{ji}}A_{\text{ji}}^{2}} - \rho_{\text{ji}}g(\Delta z_{\text{j}} + \Delta z_{\text{j} - 1})/2 \\ - \frac{{\overline{w}}_{\text{ji}}^{2}}{{\overline{\rho}}_{\text{ji}}A_{\text{ji}}^{2}} + \frac{w_{\text{ji}}^{2}}{\rho_{\text{ji}}A_{\text{ji}}^{2}} - \frac{w_{\text{ji}}^{2}}{\rho_{\text{ji}}A_{\text{j} - 1,\text{i}}^{2}} + \frac{{\overline{w}}_{\text{j} - 1,\text{i}}^{2}}{{\overline{\rho}}_{\text{j} - 1,i}A_{j - 1,\text{i}}^{2}} - \frac{1}{2}\sum_{\text{k}}\lbrack(1 - S_{\text{wjik}})w_{\text{Ljik}}(\frac{w_{\text{jk}}}{{\overline{\rho}}_{\text{jik}}A_{\text{ji}}A_{\text{jk}}} \\ - \frac{w_{\text{ji}}}{{\overline{\rho}}_{\text{jik}}A_{\text{ji}}^{2}}) + (1 - S_{\text{wj} - 1,\text{ik}})w_{\text{Lj} - 1,\text{ik}}(\frac{w_{\text{j} - 1,\text{k}}}{{\overline{\rho}}_{\text{j} - 1,\text{ik}}A_{\text{j} - 1,\text{i}}A_{\text{j} - 1,\text{k}}} - \frac{w_{\text{j} - 1,\text{k}}}{{\overline{\rho}}_{\text{j} - 1,\text{ik}}A_{\text{j} - 1,\text{i}}^{2}})\rbrack \\ \end{matrix}\end{split}\]

The energy equation for the coolant is

(3.14-3)

\[V_{\text{cji}}C_{\text{prefji}}\frac{\text{d}}{\text{dt}}\lbrack{\overline{\rho}}_{\text{ji}}({\overline{T}}_{\text{ji}} - T_{\text{r}})\rbrack = \sum_{\text{in}} w_{\text{inji}}(T_{\text{inji}} - T_{\text{r}})C_{\text{prefji}} - \sum_{\text{out}}w_{\text{outji}}(T_{\text{out}} - T_{\text{r}})C_{\text{prefji}} + \phi_{\text{ji}}\]

The energy equation in the fuel is

(3.14‑4)

\[\rho_{\text{f}}C_{\text{f}}\frac{\text{dT}_{\text{f}}}{\text{dt}} = \frac{1}{r}\frac{\text{d}}{\text{dr}}(k_{\text{f}}r\frac{\text{dT}_{\text{f}}}{\text{dr}}) + Q\]

A similar equation is used for the cladding, and a bond gap conductance is used between the fuel outer surface and the cladding inner surface. In the above equations:

\(A\) = coolant flow area in the subchannel

\(C_{\text{f}}\) = heat capacity of the fuel

\(C_{\text{pref}}\) = coolant heat capacity, evaluated at \(T_{\text{r}}\)

\(g\) = acceleration of gravity

\(i\) = subchannel number

\(j\) = axial node number

\(k\) = subchannel number of a connecting subchannel

\(k_{\text{f}}\) = fuel thermal conductivity

\(K_{\text{or}}\) = orifice coefficient

\(\Delta p_{\text{frji}}\) = friction pressure drop in the bottom half of node j and the top half of node j-1

\(Q\) = heat source per unit volume in the fuel

\(S_{\text{wjik}}\) = 1 if \(w_{\text{ljik}} \geq 0\),

0 otherwise

\(t\) = time

\(T_{\text{f}}\) = fuel temperature

\(T_{\text{in}}\) = temperature of coolant entering the node, either from another axial node in the same subchannel or from a connecting subchannel

\(T_{\text{out}}\) = temperature of coolant leaving the node

\(T_{\text{r}}\) = reference temperature, \(\overline{T}\), at the beginning of the time step is used for \(T_{\text{r}}\).

\(V_{\text{c}}\) = coolant volume in the axial node

\(z\) = axial distance

\(\rho_{\text{j}}\) = coolant density at the bottom of node j

\({\overline{\rho}}_{\text{j}}\) = coolant density at the middle of node j

\(\rho_{\text{f}}\) = fuel density

\(\phi_{\text{ji}}\) = heat source to the coolant node

(3.14‑5)

\[\phi_{\text{ji}} = \phi_{\text{cji}} + \phi_{\gamma\text{ji}} + \phi_{\text{scji}} + \phi_{\text{chchji}}\]

\(\phi_{\text{cji}} =\) heat source from the cladding and structure surfaces to the coolant

\(\phi_{\gamma\text{ji}} =\) direct heat source to the coolant from neutrons and gamma rays

\(\phi_{\text{scji}} =\) heat source from turbulent mixing and conduction from adjacent sub- channels

\(\phi_{\text{chchj}} =\) heat source to the coolant from channel-to-channel heat transfer

Also,

(3.14‑6)

\[\phi_{\text{scji}} = \sum_{k}{\lbrack u_{1\text{ik}}}k_{\text{j}} + u_{2\text{ik}}C_{\text{j}}({\overline{w}}_{\text{ji}} + {\overline{w}}_{\text{jk}})\rbrack({\overline{T}}_{\text{jk}} - {\overline{T}}_{\text{ji}}) \Delta z_{\text{j}}\]

where

\(u_{1\text{ik}}\) = geometry factor for conduction from subchannel i to subchannel k

\(u_{2\text{ik}}\) = turbulent mixing factor

\(\Delta z_{\text{j}}\) = axial node length

The parameters \(u_{1\text{ik}}\) and \(u_{2\text{ik}}\) are geometry-dependent factors supplied by the user for the particular geometry being used.

Based on a numerical simulation [3-11] with the CFX code for a triangular array of rods, the conduction geometry factor can be obtained from

(3.14‑7)

\[u_{1\text{ik}} = 0.7774 \left( \frac{s}{L_{\text{c}}} \right)\left( \frac{P}{D} \right)\left( \frac{s}{D} \right)^{- 0.2627} \Delta z_{\text{j}}\]

where

\(s\) = gap size between subchannels

\(L_{\text{c}}\) = centroid distance between subchannels

This correlation only accounts for thermal conduction in the coolant. It may be desirable to increase \(u_{1\text{ik}}\) to account for circumferential thermal conduction in the clad and possibly conduction in the fuel.

The value for \(u_{2\text{ik}}\) can be obtained from the parameter \(\epsilon^{*}\) used by Cheng and Todreas [3-12].

(3.14‑8)

\[u_{2\text{ik}} = \frac{\epsilon^{*}_{\text{i}ή} c}{ \left( A_{\text{ci}} + A_{\text{ck}} \right)}\]

\(c = s\) = gap width

\(A_{\text{ci}}\) = coolant flow area in subchannel \(i\)

The coolant lateral flow rate is given by

(3.14‑9)

\[w_{\text{Ljik}} = K_{\text{sik}}\Delta z_{\text{j}}\frac{(w_{\text{ji}} + w_{\text{j} + 1,\text{i}})}{2} + w_{\text{Lpjik}}\]

\(K_{\text{sik}} =\) wire wrap sweeping factor

In this equation the first term is the net flow due to wire wrap sweeping, and the second term is the pressure driven subchannel-to-subchannel flow. Note that \(K_{\text{sik}}\) = 0 unless there is net sweeping from subchannel i to subchannel k. For a gap between an inner subchannel and another inner subchannel or between an inner subchannel and an edge subchannel there are two wrapper wires involved; one on each pin. The two wires sweep in opposite directions, so the net sweep flow is approximately zero. Normally the wire wrap sweeping factor is zero unless i and are both edge or corner subchannels.

The second term in equation 3.14-9 is determined by

(3.14‑10)

\[\left( \frac{L}{A} \right)_{\text{Lat}} \frac{\text{dw}_{\text{Lpjik}}}{\text{dt}} = {\overline{p}}_{\text{ji}} - {\overline{p}}_{\text{jk}} - \frac{w_{\text{Lpjik}}|w_{\text{Lpjik}}|}{2{\overline{\rho}}_{\text{jik}}A_{\text{L}}^{2}}K_{\text{Lat}} \text{ if } |{\overline{p}}_{\text{ji}} - {\overline{p}}_{\text{jk}}|\ > \ \Delta p_{\text{lam}}\]

or

(3.14‑11)

\[\left( \frac{L}{A} \right)_{\text{Lat}} \frac{\text{dw}_{\text{Lpjik}}}{\text{dt}} = {\overline{p}}_{\text{ji}} - {\overline{p}}_{\text{jk}} - K_{\text{Lat}}\frac{w_{\text{lam}}w_{\text{Lpjik}}}{2{\overline{\rho}}_{\text{jik}}A_{\text{L}}^{2}} \text{ otherwise}\]

where

\(K_{\text{Lat}}\) = effective lateral flow orifice coefficient

\(\left( \frac{L}{A} \right)_{\text{Lat}}\) = lateral inertia term

\(\Delta p_{\text{lam}}\) = user specified transition pressure difference

and

(3.14‑12)

\[w_{\text{lam}} = \frac{2{\overline{\rho}}_{\text{jik}}A_{\text{L}}^{2}}{K_{\text{Lat}}}\Delta p_{\text{lam}}\]

\(K_{\text{sik}}\) is supplied by the user. It can be obtained from the parameter \(C_{1\text{L}}\) used by Cheng and Todreas:

\(K_{\text{sik}} = c C_{1\text{L}}/A_{\text{c}}\)

Cylindrical geometry with radial heat conduction is used for calculating the fuel pin temperatures. Figure 3.14.3 shows the radial node structure used for a fuel pin.

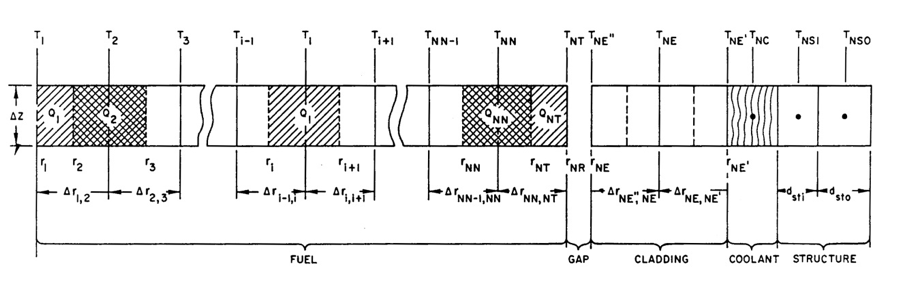
Figure 3.14.3 Radial Node Structure Used for a Fuel Pin, with Coolant and Structure

For an interior fuel node, \(1 < i < \text{NT}\), the conduction equation (equation 3.14-4) becomes:

(3.14‑13)

\[m_{\text{fi}}C_{\text{fi}}\frac{\text{dT}_{\text{fi}}}{\text{dt}} = 2\pi r_{\text{i} + 1}{\overline{k}}_{\text{i,i} + 1}(T_{\text{i} + 1} - T_{\text{i}}) + 2\pi r_{\text{i}}{\overline{k}}_{\text{i} - 1,\text{i}}(T_{\text{i} - 1} - T_{\text{i}}) + Q_{\text{i}}\]

where

\(m_{\text{fi}}\) = fuel mass per unit height in node i

\(Q_{\text{i}}\) = heat source per unit height in node i

\({\overline{k}}_{\text{i,i} + 1}\) = effective average thermal conductivity for heat flow from node i to i+1

Similar equations are used for node 1, node NT and the cladding.

3.14.3. Numerical Procedures

The solution methods used for the subchannel treatment are dictated by stability requirements and by the features that the model includes. In the coolant, a compressible treatment is desired to provide the pressures to drive subchannel-to-subchannel flow rates. Equation 3.14-1 above implies a compressible treatment. With a compressible treatment and using explicit time differencing, the Courant limit would apply. The sonic speed in sodium is about 2400 m/s. A typical axial node size is 0.03 m. Thus the Courant limit would restrict the time step size to about \(10^{- 5}\) seconds or less. To avoid such a small limit, an implicit solution is used. For one time step, the pressures and flows in all channels representing a subassembly are solved for simultaneously.

For the coolant temperatures a similar limit applies. The stability limit for an explicit solution is given by the axial node size divided by the coolant velocity. A node size of 0.03 m and a coolant velocity of 7 m/s corresponds to a limit of about 0.004 seconds. Thus, implicit time differencing is also used in this case and the coolant temperatures in a subassembly are solved for simultaneously. Also, it is probably necessary to solve for coolant temperatures simultaneously with the pressures and flows in order to obtain a stable solution. Therefore, all coolant temperatures, pressures, and flows in a subassembly are solved for simultaneously. Fortunately the situation with subassembly-to-subassembly heat transfer is different. In the PRISM design the hex can wall thickness is 0.0039 m, and the duct gap is 0.0043 m, giving a stability limit of about 2.6 seconds for explicit can wall-to-can wall heat transfer. Therefore, the subassembly-to-subassembly heat transfer can be treated explicitly, using conditions at the beginning of the time step. This means that for a given time step each subassembly can be treated separately using time step sizes of 1.0 second or more.

The steady-state calculation begins with an initial approximation of the steady-state coolant temperatures, pressures, and flow rates for each subassembly where the heat flux from each fuel pins to the coolant is determined by the steady-state pin power. Then a null transient is run for each subassembly separately, neglecting subassembly-to-subassembly heat transfer. Finally, a null transient with subassembly-to-subassembly heat transfer is run for all subassemblies. During both null transients the powers and subassembly coolant inlet flows are held constant. After the coolant conditions are calculated, the fuel pin and structure temperatures are calculated.

A time step approach is used both for the steady-state null transient and for the regular transient. Conditions are known at the beginning of the time step, and the main computational task is to determine the conditions at the end of the step. The equations are linearized about values at the beginning of the time step, and fully implicit finite differencing in time is used for the basic conservation equations. This leads to N linear equations in N unknowns. The unknowns are solved for by iteration. Explicit time differencing is used for the subassembly-to-subassembly heat transfer, so the calculations for one time step for each subassembly can be done independently.

For a transient time step the heat flux from the fuel pins and structure to the coolant is approximated as

(3.14‑14)

\[\phi_{\text{cji}} = \phi_{\text{c}1\text{ji}} + \phi_{\text{c}2\text{ji}}\Delta{\overline{T}}_{\text{ji}}\]

for the coolant calculations. The coefficients \(\phi_{\text{c}1}\) and \(\phi_{\text{c}2}\) are calculated in the fuel pin heat transfer routines. In this equation \(\Delta T\) is the change in coolant temperature during the time step. After the coolant temperatures are calculated, the fuel pin and structure temperatures are calculated for the time step.

3.14.4. Interfacing with Other Models in the Code

This section summarizes the interfacing between the existing SAS4A/SASSYS‑1 code and the new three-dimensional thermal hydraulics core model. The main interactions between the new model and the rest of the code are with the input module, output module, neutronics module, DEFORM-5 fuel pin mechanics module for metal fuel, simple PRIMAR-1 primary loop module, and detailed PRIMAR-4 module for the primary and intermediate heat transfer loops. These interactions and the interface data requirements are discussed in the sections below.

Note that the new subchannel model is only applicable to single-phase coolant with intact fuel pins. The SAS4A/SASSYS‑1 sodium boiling model and PLUTO and LEVITATE disrupted fuel pin modules cannot be used in the same subassembly as the coolant subchannel module.

3.14.4.1. Input Module

The SAS4A/SASSYS‑1 code reads input into numbered locations in input blocks. Extra space has been provided in these input blocks for future use by new modules. Some of this extra space is used by the new input variables for the new three dimensional thermal hydraulics core module. The new module also uses many existing input variables. There is enough extra space in each input block to accommodate the new variables. No modifications are required to the input module for use with the new module. The new input variables are listed in the user guide section below.

3.14.4.2. Output Module

The output files for a whole-core case using the new model can get very large because of the large number of channels involved. Therefore, some modification of the output module has been necessary. For the printed output one change that was necessary was to print reactivity feedback by subassembly rather than by channel. Output on CHANNEL.dat is binary data intended for input to plotting programs. Previously one record per channel per time step was put on CHANNEL.dat. This has been modified to output every N time steps for specified channels or subassemblies.

3.14.4.3. Neutronics Module

The neutronics module uses fuel, cladding, and coolant temperatures and coolant densities from the core thermal hydraulics module to obtain reactivity feedback components at the end of each transient main time step. For each transient step, the neutronics module supplies the core thermal hydraulics module with the power level. The coupling with the neutronics module is the same for the new three dimensional thermal hydraulics core module as for the older core thermal hydraulics module.

3.14.4.4. DEFORM-5 Fuel Pin Mechanics for Metal Fuel

The DEFORM-5 module uses fuel and cladding temperatures from the core thermal hydraulics module for its prediction of pin failure. The coupling with the DEFORM-5 module is the same for the new three-dimensional thermal hydraulics core module as for the older core thermal hydraulics module.

3.14.4.5. PRIMAR-1

SAS4A/SASSYS‑1 uses either the simple PRIMAR-1 primary loop module or the detailed PRIMAR-4 module for the primary and intermediate heat transport systems. When PRIMAR-1 is used, the initial steady-state subassembly inlet pressure and average core outlet temperature calculated by the core thermal hydraulics module are used by PRIMAR-1 to obtain the initial steady-state primary loop gravity head and pump head. During the transient calculation, PRIMAR-1 provides the subassembly inlet pressure and inlet temperature to the core thermal hydraulics module. No transient information from the core thermal hydraulics module is used by PRIMAR-1.

3.14.4.6. PRIMAR-4

The core thermal hydraulics module and PRIMAR-4 are tightly coupled, and the transient coupling with PRIMAR-4 required more effort in the development of the new core thermal hydraulics module than the coupling with any other module. This coupling also contributes significantly to the running time of the new module.

The steady-state coupling between the core thermal hydraulics and PRIMAR-4 is similar to the coupling with PRIMAR-1. The user specifies the subassembly outlet pressure and inlet temperature in the input. The initial coolant flow rate in each channel is also specified by the user. Then the core thermal hydraulics module calculates the outlet temperature and inlet pressure for each subassembly. Inlet orifice coefficients are adjusted so that the inlet pressures for all subassemblies match the maximum inlet pressure. The subassembly inlet and outlet pressures, inlet temperatures and average outlet temperature are used in the steady-state PRIMAR-1 and PRIMAR-4 calculations. This steady-state coupling is the same with the new core thermal hydraulics model.

During the transient calculation, PRIMAR-4 provides the subassembly inlet pressure and inlet temperature to the core thermal hydraulics module in the same way that PRIMAR-1 does. The big difference between the coupling with PRIMAR-4 and PRIMAR-1 is that during a transient time step, PRIMAR-4 estimates the core flows and outlet temperatures before they are calculated by the core thermal hydraulics module. With the previous thermal hydraulics module at the end of each PRIMAR time step, the core module calculates the coefficients \(C_{0},C_{1},C_{2,}\) and \(C_{3}\) for each channel for use by PRIMAR-4. At the beginning of the next PRIMAR time step, PRIMAR-4 gets the channel flow rates from the core thermal hydraulics module and estimates the channel flow at the end of the step using

(3.14‑15)

\[\frac{\text{dw}_{\text{Li}}}{\text{dt}} = C_{0\text{Li}} + C_{1\text{Li}}p_{\text{in}} + C_{2\text{Li}}p_{\text{x}} + C_{3\text{Li}}w_{\text{Li}}|w_{\text{Li}}|\]

where

\(w\) = coolant flow rate

\(t\) = time

\(L\) = 1 for the subassembly inlet, 2 for the subassembly exit

\(i\) = channel number

With the new core thermal hydraulic treatment, at the beginning of each transient PRIMAR-4 time step, after the time step size has been determined, the core thermal hydraulics module is called to provide new coefficients \(a_{0},\ a_{1}\) and \(a_{2}\) for each subassembly. PRIMAR-4 then estimates the coolant flow at the end of the PRIMAR step using

(3.14‑16)

\[w_{\text{Ln}} \left( t_{\text{p}} + \Delta t \right) = w_{\text{Ln}} \left( t_{\text{p}} \right) + \left( a_{0\text{Ln}} + a_{1\text{Ln}}\Delta p_{\text{in}} + a_{2\text{Ln}}\Delta p_{\text{x}} \right) \Delta t\]

where

\(n\) = subassembly number

\(t_{\text{p}}\) = time at beginning of the PRIMAR step

\(\Delta t\) = PRIMAR time step size

\(\Delta p_{\text{in}}\) = change in inlet pressure during the PRIMAR step

\(\Delta p_{\text{x}}\) = change in outlet plenum pressure during the PRIMAR step

Note that with the proper choice of values for the coefficients, Equation 3.14-15 and Equation 3.14-16 can be made approximately equivalent, but there are two significant differences between them. First when using the previous core thermal hydraulics module, the C’s are calculated for each channel, based on the assumption that one channel represents one or more subassembly. With the new core thermal hydraulics module, a number of channels can be used to represent one subassembly, and the a’s of Equation 3.14-16 are calculated for each subassembly rather than for each channel. Second, the coefficients in Equation 3.14-15 are calculated before the new PRIMAR time step size is known; and the coefficients are independent of time step size. On the other hand, the coefficients in Equation 3.14-16 are calculated after the new PRIMAR time step size is known, and they may depend on the size of the time step. The previous core thermal hydraulics module uses incompressible coolant flow, whereas the new module uses a compressible treatment for the coolant. With an incompressible treatment, it is possible to obtain C’s for Equation 3.14-15 that are approximately correct for any reasonable time step size. On the other hand, with a compressible treatment the values of the coefficients in Equation 3.14-16 will depend strongly on whether or not the time step is large enough for a sound wave to travel from one end of the subassembly to the other and back in the time step.

3.14.5. Data Management

A very flexible data management scheme is required for the detailed subchannel model because of the range of size of the cases that will be run and because a lot of the data is needed simultaneously in the solution. The range of sizes of the cases expected to be run with the model is very large: from a single subassembly containing a few pins and a few coolant subchannels to a large whole core case containing hundreds of subassemblies with hundreds of channels per subassembly. Also, in the calculations for a time step the equations for all channels in a subassembly are solved simultaneously, requiring simultaneous access to the data for all of the channels in the subassembly.

In order to provide the flexibility needed by the model, most of the data is stored in dynamically allocated storage containers whose sizes are determined at run time based on the size of the case being run. A structured pointer system is used to access the data. The permanent channel dependent variables, which are saved from one time step to the next, are stored in a large container and accessed with channel-dependent pointers. The temporary variables used in the simultaneous solution for all of the channels in a subassembly are stored in a number of containers also accessed with pointers. Thus small cases can be run with a small amount of memory, and the available memory can be apportioned efficiently to run large cases without re-compiling the code.

3.14.6. Coding Overview and Subroutines

Figure 3.14.4 shows an overview of the steady-state calculations.

Figure 3.14.4 Coding Overview of the Steady-State Calculation for the Detailed Subchannel Model

Figure 3.14.5 shows an overview of the transient calculations for the model. It should be noted that SSHTR is a previously existing routine in the SAS4A/SASSYS‑1 code. Also, TSHTSC is based mainly on the previously existing routine TSHTRV, with some modifications. Listings of the subroutines used in the new model are given in Table 3.14.1, Table 3.14.2, and Table 3.14.3.

Figure 3.14.5 Coding Overview for One Time Step of the Transient Calculation for the Detailed Subchannel Model

Table 3.14.1 New Subroutines - Detailed Coolant Subchannel Model

Subroutine	Description
CHCHFL	Calculates subassembly-to-subassembly heat flow from the outer structure node of channel i to the outer structure node of channel j. Also contains an option to transfer heat from the outer structure node of channel i to the coolant of channel j. In the future this subroutine will be modified to include an option to transfer heat from the outer structure node of channel i to a constant temperature heat sink. This is a modified version of a SAS4A/SASSYS‑1 subroutine.
COOLFN	Finishes the coolant calculations for one time step for one group of channels after SOLVIT has calculated the changes in the main variables.
COOLPT	Prints the coolant results for one channel at the end of a time step.
DYNAL2	Dynamic storage allocation for containers for temporary storage for the coolant model.
INVTRI	Solves a general tri-diagonal matrix equation.
LATPRT	Prints coolant lateral flow rates.
SBFT24	Writes selected binary output on unit 24. Section 3.15.3.1.4 has more detail on the unit 24 output.
SCCOEF	Calculates the coefficients of the linearized equations for the coolant model for one group of channels for one time step.
SOLVIT	Solves the equations set up by SCCOEF to obtain the changes in the coolant independent variables for a time step.
SSMPDR	Steady-state driver for the detailed coolant subchannel model. Calculates initial approximate values for coolant variables. Then runs a null transient for each subassembly without subassembly-to-subassembly heat transfer. Finally runs a null transient for the whole core with subassembly-to-subassembly heat transfer.
SSNLSC	Driver for the steady-state null transient with subassembly-to-subassembly heat transfer.
SSSTR	Calculates steady-state temperatures in the structure and in the reflectors.
TSHTSC	Calculates transient temperatures in the fuel pins. Also calculates structure and reflector temperatures. A modified version of TSHTRV from SAS4A/SASSYS‑1.
TSMPDR	Transient driver for the detailed subchannel model. Calculates one coolant time step for one group of channels.

Table 3.14.2 SAS4A/SASSYS‑1 Subroutines Used with Detailed Subchannel Model

Subroutine	Description
CCLAD	Cladding heat capacity.
CFUEL	Fuel heat capacity.
DATMOV	Copies data packs from the dynamically allocated memory container to the regular common blocks and moves them back.
HBSMPL	Simple model for the bond gap conductance between the fuel and the cladding.
INVRT3	Solves a tri-diagonal matrix equation for temperatures. Note, INVRT3 and INVTRI have similar uses, but INVTRI can handle a more general tri-diagonal matrix.
KFUEL	Calculates fuel thermal conductivity.
LINES	Counts the number of lines that have been printed and puts page headings in the output.
POINST	Calculates pointers used by DATMOV and in the memory management.
READIN	Reads the input data
RESTAR	Reads or writes a restart file.
SHAPE	Sets the axial power shape in the fuel pin section of a channel.
SSCOOL	Calculates steady-state coolant temperatures and pressures ignoring subchannel-to-subchannel cross flow and heat transfer. Used for initial conditions for the steady-state null transient.
SSHRT	Steady-state fuel pin temperatures.
TSHTN5	Calculates melting of the cladding.
TSHTN6	Calculates melting of the fuel.
TSPRNT	Prints thermal hydraulic output for selected channels.

Table 3.14.3 SAS4A/SASSYS‑1 Drivers that Call Detailed Subchannel Model

Subroutine	Description
INPDRV	Input driver, calls READIN
SSTHRM	Steady-state thermal hydraulics driver for the core channel calculations.
TSTHRM	Transient thermal hydraulics driver for the core channel calculations.

3.14.7. Required Computer Capabilities

One question that has been addressed is whether it is practical to run a detailed whole core case on currently available computers. There are two main computer-related considerations. One consideration is whether currently available computers have enough memory for a whole core case. The other consideration is whether computers are fast enough to run a large case in a reasonable amount of time.

3.14.7.1. Memory Requirements

For the detailed subchannel model the SAS4A/SASSYS‑1 code requires 0.13 or 0.17 MB of main memory per channel, depending on whether or not the fuel pin mechanics model in the code is used in addition to the subchannel thermal hydraulics model. An additional 8 MB are used for coding, and a few MB are used for non-channel dependent memory.

To determine how many channels are required for a detailed treatment, consider the ALMR mod B reactor design, which is a moderately sized reactor, with a power rating of 840 MWt. This reactor contains 108 driver subassemblies with 271 pins and 546 coolant subchannels per subassembly, 84 blanket subassemblies with 127 pins and 258 coolant subchannels per subassembly, 66 shield subassemblies with 7 pins and 18 coolant subchannels per subassembly, and a few other subassemblies. With a one computational channel per subchannel treatment, a whole core case could therefore use about 81,000 channels. This would require 10.5 - 13.8 GB of memory, although if the core loading is symmetrical the number of computational channels and the memory requirements could be reduced by making use of the symmetry. Liquid metal reactor designs about four times as large as the ALMR reactor have been considered. A detailed analysis of such a design might require 40 - 50 GB of memory. Some current computers are limited to a maximum of 2 GB of memory, although many computers have more memory. Accessing more than 2 GB of memory would probably require the use of 64 bit integers.

3.14.7.2. Speed Considerations

Timing data for the new detailed subchannel model indicates that the time required on an old Sun Blade computer with a processor speed of 500 MHz is about 8 ms per time step per channel. Thus, even if this computer had enough memory to run the 81,000 channel ALMR case discussed above, the time required for a solution for 1000 time steps could be 650,000 seconds, or 7.5 days. Computers with processor speeds significantly greater than 500 MHz are currently available, but it appears that running a large case will require significant amounts of computing power and running time.

3.14.7.3. Use of a Multi-Processor Cluster

Because of the memory and speed considerations listed above, it might appear that the most practical way to run large cases with the new model is with the use of a cluster of processors, with one or more subassemblies run on each processor. The model was developed with that in mind. However, the older modules in SAS4A/SASSYS‑1 were written before clusters of processors were being considered, and converting the whole code to run on multiple processors would require a great effort. Currently the approach is to model part of the core with the detailed subchannel model and to model the rest of the core with the older, less detailed models which require considerably less memory and computing time. This approach works well with the current code and current computers. High-end currently available computers have enough memory and speed to run large detailed subchannel cases on a single computer.