3.3. Pre-boiling Transient Heat Transfer, Single Pin Model

The transient fuel-pin temperature calculations in SAS4A/SASSYS‑1 are similar to the Crank-Nicolson scheme [3-1] used in SAS2A [3-2] and SAS3D [3-3], but there are a number of significant differences. One reason for these differences is to allow the use of larger heat-transfer time steps with less computing time per step. Another reason is to obtain greater accuracy and more precise energy balance.

In order to use very long heat-transfer time steps on one second or more in the pre-voiding phase of a very slow transient, the fuel, cladding, coolant, and structure temperatures at an axial node are computed simultaneously in non-voiding cases. Therefore, coolant temperatures are computed in the fuel-pin heat-transfer routine in the non-voiding situation.

The coupling between TSHTRN and the pre-voiding coolant dynamics routines is different from the coupling between TSHTRV and the voiding routines, although in both cases the coolant dynamics or voiding calculations are done before the fuel-pin heat-transfer calculations. In the non-voiding case, extrapolated coolant temperatures are used to obtain the temperature-dependent sodium properties used in the calculation of the coolant flow rates and heat-transfer coefficients. Then, TSHTRN uses these values to compute the coolant temperatures, and these new coolant temperatures are used in the next extrapolation. In the voiding routines, extrapolated cladding temperatures are used in the implicit calculation of the heat flux from cladding to coolant to obtain new coolant temperatures. The voiding routines then sum the integrated heat flux from cladding to coolant at each axial node, and this integrated heat flux at the cladding surface is used as a boundary condition in TSHTRV.

TSHTRN and TSHTRV are somewhat simpler than the corresponding TSHTR in SAS3A and SAS3D. In SAS3D, TSHTR contains extraneous material related to other modules, such as initiating cladding and fuel motion; this material is not included in the SAS4A/SASSYS‑1 heat-transfer routines. Also, in SAS3D, the fuel mass for each radial node of each axial node is recomputed every time step from the temperature-dependent fuel density and the node radii. In SAS4A/SASSYS‑1 the node mass is computed in the steady-state module and then stored for used in the transient. This node mass is held constant until fuel relocation starts.

Another difference between the SAS3D and SASSYS-1 heat-transfer routines is in the amount of vectorization of the algorithms and the coding. Some of the calculations in the SAS3D routines happen to vectorize, but a special effort was made to vectorize many more of the calculations in the SAS4A/SASSYS‑1 heat-transfer routines. In general, vectorizing involves setting up arrays so that all elements in the array are processed in the same way and so that the results of a given calculation for one element in the array do not depend on the results for any other element in the array. Vectorization is partly just a coding matter, but it also involves choosing vectorizable algorithms or adapting algorithms for vectorization.

To some extent, the descriptions in the following sections reflect the emphasis on vectorization. Intermediate quantities used in the solution are usually defined as elements in arrays, and, where possible, the array elements are defined so that all of the elements in an array can be treated in the same manner in the calculations. In order to emphasize the array nature of the solution, when a new array is introduced, all of the elements in the array are defined in the same section, even though many of the elements are often not used until later sections.

As indicated above in Section 3.2.2, three different radial mesh structures are used in the heat-transfer calculations: one for the core and blanket region, one for the gas plenum region, and one for the reflector regions. Different heat-transfer calculations are done for each of these three regions.

3.3.1. Core and Axial Blankets

3.3.1.1. Basic Equations

The basic transient heat-transfer equation within the fuel and within the cladding is

(3.3-1)

\[\rho c \frac{\partial \text{T}}{\partial \text{t}} = \frac{1}{r}\frac{\partial}{\partial \text{r}}\left( \text{kr} \frac{\partial \text{T}}{\partial \text{r}} \right) + Q\]

where

\(T\) = temperature

\(\rho\) = density

\(c\) = specific heat

\(r\) = radius

\(k\) = thermal conductivity

\(t\) = time

and

\(Q\) = heat source per unit volume

Melting of fuel and cladding is treated using a melting range, bounded by solidus and liquidus temperatures, \(T\)_sol and \(T\)_liq, respectively, and a heat of fusion, \(U\)_melt. Separate values of \(T\)_sol, \(T\)_liq, and \(U\)_melt are used for the fuel and cladding. In the melting range, Eq. 3.3-1 is modified and becomes

(3.3‑2)

\[\rho c_{\text{m}}\frac{\partial \text{T}}{\partial \text{t}} = \frac{1}{r}\frac{\partial}{\partial \text{r}}\left( \text{kr}\frac{\partial \text{T}}{\partial \text{r}} \right) + Q\]

where

(3.3‑3)

\[c_{\text{m}} = \frac{U_{\text{melt}}}{T_{\text{liq}} - T_{\text{sol}}}\]

In the actual solution of Eq. 3.3-2 for a time step, \(c\) is used instead of \(c_{\text{m}}\) in the calculation of the temperature change for the step. Then, if the temperatures are in the melting range, the computed temperature change is modified to account for the heat of fusion, as described in Section 3.3.5.

The heat flux, \(q_{\text{fe}}\), from the fuel outer surface to the cladding inner surface contains both a bond gap conductance term, \(h_{\text{b}}\), and a radiation term:

(3.3‑4)

\[q_{\text{fe}} = h_{\text{b}}\left\lbrack T\left( \mathrm{\text{NT}} \right) - T\left( \text{NE}'' \right) \right\rbrack + \epsilon \sigma \left\lbrack T\left( \mathrm{\text{NT}} \right)^{4} - T\left( \text{NE}'' \right)^{4} \right\rbrack\]

where

\(\epsilon\) = thermal emissivity of the fuel

\(\sigma\) = Stefan-Boltzmann constant

\(T\)(NT) = fuel outer surface temperature

and

\(T\)(NE’’) = cladding inner surface temperature

For the coolant, the basic heat-transfer equation is

(3.3‑5)

\[\rho c ~A_{\text{c}}\frac{\partial \text{T}}{\partial \text{t}} + \frac{\partial}{\partial \text{z}}\left( \text{wcT} \right) = \left( Q_{\text{c}} + Q_{\text{ec}} + Q_{\text{sc}} \right)A_{\text{c}}\]

where \(A_{\text{c}}\) = coolant flow area. The heat, \(Q_{\text{c}}\), produced directly in the coolant is computed from the fraction, \(\gamma_{\text{c}}\), of the total energy production that goes into neutron and gamma heating of the coolant:

(3.3‑6)

\[Q_{\text{c}} = \frac{\gamma_{\text{c}}\overline{P}(j)}{A_{\text{c}}\Delta z(j)}\]

where

\(\overline{P}\left( j \right)\) = total heat production rate in axial node j

and

\(\Delta z(j)\) = axial node height

The heat flow from the cladding to the coolant, \(Q_{\text{ec}}\) is calculated as

(3.3‑7)

\[Q_{\text{ec}} = h_{\text{c}}\left\lbrack T\left( \mathrm{N}\text{E}' \right) - T(\mathrm{\text{NC}}) \right\rbrack\frac{2 \pi r(\mathrm{N}\text{E}')\ }{A_{\text{c}}}\]

and the heat flow from structure to coolant, \(Q_{\text{sc}}\), is calculated as

(3.3‑8)

\[Q_{\text{sc}} = h_{\text{c}}\left\lbrack T\left( \mathrm{\text{NSI}} \right) - T(\mathrm{\text{NC}}) \right\rbrack\frac{S_{\text{st}}}{A_{\text{c}}}\]

where \(S_{\text{st}}\) is the perimeter of the structure. The coolant heat-transfer coefficient, \(h_{c}\), is calculated using

(3.3‑9)

\[\frac{h_{\text{c}}D_{\text{h}}}{k} = c_{1}\left\lbrack \frac{D_{\text{h}}~\text{w c}}{\text{k}~A_{\text{c}}} \right\rbrack^{c_{2}} + ~c_{3}\]

which is a form used in correlations for convective heat-transfer coefficients for low Prandtl number fluids, such as liquid metal [3-4]. The user supplied constants \(c_1\), \(c_2\), and \(c_3\) depend on the particular correlation used.

The structure is treated with a one-dimensional heat conduction equation:

(3.3‑10)

\[\rho c \frac{\partial \text{T}}{\partial \text{t}} = \frac{\partial}{\partial \text{x}}\left\lbrack k\ \frac{\partial \text{T}}{\partial \text{x}} \right\rbrack + Q\]

The treatment of the heat source, \(Q\), in the structure is discussed in Section 3.3.1.2.8.

3.3.1.2. Finite Difference Equations

Finite differencing in both space and time is used for the transient heat-transfer calculations. The radial mesh structure is described in Section 3.2.2 above. In the equations below, the time t represents the beginning of the temp step, and \(\Delta t\) is the step size. The parameters \(\theta_1\) and \(\theta_2\) determine the degree of implications. For an explicit scheme, \(\theta_1\) = 1.0 and \(\theta_2\) = 0.0. For a fully implicit scheme, \(\theta_1\) = 0.0 and \(\theta_2\) = 1.0. For a semi-implicit scheme \(\theta_1\) = 0.5 and \(\theta_2\) = 0.5. The degree of implicitness is calculated by the code, based on the ratio of the time-step size, \(\Delta t\), to a user-supplied time constant for fuel-pin heat transfer, \(\tau_{\text{ht}}\). As explained in Section 3.19.1, the expression used for \(\theta_1\) and \(\theta_2\) in TSHTRN are

(3.3-11a)

\[\theta_{2} = \frac{1.65 + x}{3.3 + x}\]

where

(3.3‑11b)

\[x = \frac{\Delta t}{\tau_{\text{ht}}}\]

and

(3.3‑12)

\[\theta_{1} = 1.0 - \theta_{2}\]

Also, large relative changes in coolant flow rate, w, during a long heat transfer time step can lead to anomalous coolant temperature changes if the value of \(\theta_1\) is too large; therefore, \(\theta_2\) is calculated as

(3.3‑13)

\[\theta_{2} = \frac{\left| w_{1} \right|}{\left| w_{1} \right| + \left| w_{2} \right|}\]

if Eq. 3.3-13 gives a larger value than Eq. 3.3-11. In Eq. 3.3-13, \(w_1\) and \(w_2\) are the coolant flow rates at the beginning and end of the heat-transfer time step, respectively. In any case, Eq. 3.3-12 is used for \(\theta_1\).

The heat transfer time step size is limited to a relatively small value (0.02 s or less) after the onset of boiling, and so TSHTRV used \(\theta_1\) = \(\theta_2\) = 0.5.

The finite difference equations used for the fuel and for the two inner cladding nodes are the same in TSHTRN and TSHTRV. The differences between these routines start at the outer cladding node.

In general, the time derivative of a variable \(y\) is approximated as

(3.3‑14)

\[\frac{\partial \text{y}}{\partial \text{t}} = \frac{y\left( t + \Delta t \right) - y\left( t \right)}{\Delta t}\]

and the spatial derivative is approximated as

(3.3‑15)

\[\frac{\partial \text{y}}{\partial \text{z}} \simeq \theta_{1}\left\lbrack \frac{y\left( t,z + \Delta z \right) - y\left( t,z \right)}{\Delta z} \right\rbrack\ + \theta_{2}\left\lbrack \frac{y\left( t + \Delta t,z + \Delta z \right) - y\left( t + \Delta t,z \right)}{\Delta z} \right\rbrack\]

In the following sections, it will be useful to refer to Figure 3.2.4 for the radial node structure and the definitions of the radial node indexes.

3.3.1.2.1. Fuel Inner Surface, Node 1

There is an adiabatic boundary at the fuel inner surface; so the node 1, Eq. 3.3-1 becomes

(3.3‑16)

\[\begin{split}\begin{matrix} m_{\text{f}}\left( 1 \right)\ \overline{c}_{\text{f}}\left( 1 \right)\left\lbrack \frac{T_{2}\left( 1 \right) - T_{1}\left( 1 \right)}{t} \right\rbrack \\ = \frac{2\pi r \left( 2 \right) \Delta z \left( j \right)\overline{k}_{1,2}}{\Delta r_{1,2}}\left\{ \theta_{1}\left\lbrack T_{1}\left( 2 \right) - T_{1}\left( 1 \right) \right\rbrack + \theta_{2}\left\lbrack T_{2}\left( 2 \right) - T_{2}\left( 1 \right) \right\rbrack \right\} + Q(1) \\ \end{matrix}\end{split}\]

where

\(m_f (i)\) = fuel mass at node i

\(\overline{c}\left( i \right)\) = fuel heat capacity at radial node \(i\) at \(t = t_1 + \theta_2 \Delta t\)

\(T_2 (i)\) = temperature at \(t+\Delta t\)

\(T_1 (i)\) = temperature at time \(t\)

\(\Delta z (j)\) = axial mesh height

(3.3‑17)

\[\Delta r (1) = 2\left\lbrack r\left( 2 \right) - r\left( 1 \right) \right\rbrack\]

(3.3‑18)

\[\Delta r \left( i \right) = r\left( i + 1 \right) - r\left( i \right)\ \ \ \ \ \ \ 2\ \ \leq \ \ i\ \ \leq \ \ \text{NN}\]

(3.3‑19)

\[\Delta r\left( \text{NT} \right) = 2\left\lbrack r\left( \text{NR} \right) - r\left( \text{NT} \right) \right\rbrack\]

(3.3‑20)

\[\Delta r\left( i \right) = \ \frac{\left\lbrack r\left( \text{NE}' \right) - r~(\text{NE}) \right\rbrack}{2}\ \ \ i = \text{NE}'',\ \text{NE},\ \text{NE}'\]

(note: \(\text{NE}''\ = \ \text{NR}\))

(3.3‑21)

\[\Delta r_{\text{i,i} + 1} = \frac{\Delta r\left( i \right) + \Delta r\left( i + 1 \right)}{2}\ \ 1\ \ \leq \ \ i\ \ \leq \ \ \text{NE}\]

(3.3‑22)

\[Q\left( i \right) = \frac{\overline{P}\left( j \right)\left( 1 - \gamma_{\text{e}} - \gamma_{\text{c}} - \gamma_{\text{s}} \right)\ P_{\text{r}}\left( i \right)m_{\text{f}}\left( i \right)}{\sum_{\text{ii} = 1}^{\text{NT}}{~ P_{\text{r}}\left( \text{ii} \right)m_{\text{f}}\left( \text{ii} \right)}}\ \ 1\ \ \leq \ \ i\ \ \leq \ \ \text{NT}\]

(3.3‑23)

\[Q\left( \text{NE}'' \right) = \frac{\overline{P}\left( j \right)\gamma_{\text{e}}}{4}\]

(3.3‑24)

\[Q\left( \text{NE} \right) = \frac{\overline{P}\left( j \right)\gamma_{\text{e}}}{2}\]

(3.3‑25)

\[Q\left( \text{NE}' \right) = \frac{\overline{P}\left( j \right)\gamma_{\text{e}}}{4} = Q\left( \text{NE}'' \right)\]

where

\(\overline{P}\left( j \right)\) = total power (watts) in axial node j

\(P_{\text{r}} (i)\) = radial power shape per unit mass

and

\(\gamma_{\text{e}},\gamma_{\text{c}},\gamma_{\text{s}}\) = fraction of power in direct heating of clad, coolant, and structure, respectively.

The thermal conductivity, \(\overline{k}_{1,2}\) used in Eq. 3.3-16 is a weighted average of the values for the two adjacent nodes. It is calculated as

(3.3‑26)

\[{\overline{k}}_{\text{i,i} + 1} = \frac{k\left( i \right)k\left( i + 1 \right) ~ \left\lbrack \Delta r \left( i \right) + \Delta r\left( i + 1 \right) \right\rbrack}{k\left( i \right) \Delta r \left( i + 1 \right) + k\left( i + 1 \right) \Delta r \left( i \right)}\]

where

\(k(i)\) = thermal conductivity for radial node i, evaluated using the fuel temperature extrapolated to \(t + \theta_2 \Delta t\)

Equation 3.3-26 is carried over from SAS3D. The fuel restructuring algorithm used in SAS3D uses up to three different fuel types (columnar, equiaxed, and unrestructured) for the fuel at each axial node. Sharp boundaries between fuel types are used. The radial mesh is adjusted, if necessary, so that fuel-type boundaries fall on radial node boundaries. One consequence of the sharp fuel-type boundaries in SAS3D is that the fuel thermal conductivity can change significantly from one node to the next at a fuel-type boundary. The average thermal conductivity of Eq. 3.3-26 will give accurate steady-state fuel temperatures even if the thermal conductivity has large jumps at node boundaries. The fuel restructuring provided by DEFORM-IV in SAS4A is somewhat smoother than that used in SAS3D, and the node-to-node changes in thermal conductivity in SAS4A are usually smaller than the corresponding changes at fuel-type boundaries in SAS3D, so the need for special weighting of the fuel thermal conductivities in SAS4A Lis less than in SAS3D, but Eq. 3.3-26 still provides more accurate fuel temperatures than simpler weighting schemes.

Note that even though most of the variables in Eqs. 3.3-16 to 3.3-26 vary with axial node \(j\), the subscript \(j\) has only been included for some of these variables.

3.3.1.2.2. Inner Fuel Nodes, Nodes 2 to NN

For fuel radial node I, Eq. 3.3-1 becomes

(3.3‑27)

\[\begin{split} \begin{matrix} m_{\text{f}}\left( i \right)\overline{c}_{\text{f}}\left( i \right) ~ \frac{\left\lbrack T_{2}\left( i \right) - T_{1}\left( i \right) \right\rbrack}{\Delta t} \\ = \frac{2\pi r\left( i + 1 \right) \Delta z \left( j \right){\overline{k}}_{\text{i,i} + 1}}{\Delta r_{\text{i,i} + 1}}\left\{ ~ \theta_{1} ~ \left\lbrack T_{1}\left( i + 1 \right) - T_{1}\left( i \right) \right\rbrack + \theta_{2} ~ \left\lbrack T_{2}\left( i + 1 \right) - T_{2}\left( i \right) \right\rbrack ~ \right\} \\ - \frac{2\pi r\left( i \right) \Delta z \left( j \right){\overline{k}}_{\text{i} - 1,\text{i}}}{\Delta r_{\text{i} - 1,\text{i}}}\left\{ ~ \theta_{1} ~ \left\lbrack T_{1}\left( i \right) - T_{1}\left( i - 1 \right) \right\rbrack + \theta_{2} ~ \left\lbrack T_{2}\left( i \right) - T_{2}\left( i - 1 \right) \right\rbrack ~ \right\} + Q\left( i \right) \\ \end{matrix}\end{split}\]

Note that the left-hand side of Eq. 3.3-27 represents the change in internal energy as node \(i\), whereas the terms on the right-hand side represent heat conduction into node \(i\) from nodes \(i+1\) and \(i-1\), as well as the heat source in node \(i\).

3.3.1.2.3. Fuel Outer Surface Node, Node NT

The heat flux \(q_{\text{fc}}\), from the fuel outer surface to the cladding inner surface contains both a bond gap conductance and a radiation term.

(3.3‑28)

\[q_{\text{fc}} = h_{\text{b}}\left\lbrack \text{T}\left( \text{NT} \right) - \text{T}\left(\text{NE}'' \right) \right\rbrack + \varepsilon\sigma\ \ \left\lbrack \text{T}\left( \text{NT} \right)^{4} - \text{T}\left( \text{NE}'' \right)^{4} \right\rbrack\]

where

\(h_{\text{b}}\) = bond conductance

\(\epsilon\) = thermal emissivity of the fuel

and

\(\sigma\) = Stefan-Boltzmann constant.

The \(T^4\) terms are rewritten as

(3.3‑29)

\[T\left( \text{NT} \right)^{4} - T\left( \text{NE}'' \right)^{4} = h_{\text{r}}\left\lbrack T\left( \text{NT} \right) - T\left( \text{NE}'' \right) \right\rbrack\]

where

(3.3‑30)

\[h_{\text{r}} = \frac{T_{1}\left( \text{NT} \right)^{4} - T_{1}\left( \text{NE}'' \right)^{4}}{T_{1}(\text{NT}) - T_{1}(\text{NE}'')} = \left\lbrack T_{1}\left( \text{NT} \right) + T_{1}\left( \text{NE}'' \right) \right\rbrack\left\lbrack T_{1}\left( \text{NT} \right)^{2} + T_{1}\left( \text{NE}'' \right)^{2} \right\rbrack\]

The approximation is then made that \(h_\text{r}\) is a constant for a time step, and the equation for node NT becomes

(3.3‑31)

\[\begin{split}\begin{matrix} m_{\text{f}}\left( \text{NT} \right){\overline{c}}_{\text{f}}\left( \text{NT} \right)\ \frac{T_{2}\left( \text{NT} \right) - T_{1}(\text{NT})}{\Delta t} = \frac{2\pi r\left( \text{NT} \right) \Delta z \left( j \right){\overline{k}}_{\text{NN,NT}}}{\Delta r_{\text{NN,NT}}} \left\{ \theta_{1}\left\lbrack T_{1}\left( \text{NN} \right) - T_{1}\left( \text{NT} \right) \right\rbrack + \\ \theta_{2}\left\lbrack T_{2}\left( \text{NN} \right) - T_{2}\left( \text{NT} \right) \right\rbrack \right\}\ + 2 \pi r \left( \text{NR} \right) \Delta z \left( j \right)\left\lbrack h_{\text{b}} + \epsilon\sigma h_{\text{r}} \right\rbrack\ \left\{ \theta_{1}\left\lbrack T_{1}\left( \text{NE}'' \right) - T_{1}(\text{NT}) \right\rbrack \right.\ \left. \ \\ + \theta_{2}\left\lbrack T_{2}\left( \text{NE}'' \right) - T_{2}(\text{NT}) \right\rbrack \right\} + Q\left( \text{NT} \right) \end{matrix}\end{split}\]

3.3.1.2.4. Cladding Inner Node, Node \(\text{NE}''\)

For the cladding inner node, Eq. 3.3-1 becomes

(3.3‑32)

\[\begin{split} \begin{matrix} \frac{m_{\text{e}}c_{\text{e}}}{4}\frac{T_{2}\left( \text{NE}'' \right) - T_{1}\left( \text{NE}'' \right)}{\Delta t} \\ = \frac{2\pi\Delta z\left( j \right){\overline{r}}_{\text{NE}}\ k_{\text{NE}'',\text{NE}}}{\Delta r_{\text{NE}'',\text{NE}}}\left\{ \theta_{1}\ \left\lbrack T_{1}\left( \text{NE} \right) - T_{1}\left( \text{NE}'' \right) \right\rbrack + \theta_{2}\ \left\lbrack T_{2}\left( \text{NE} \right) - T_{2}\left( \text{NE}'' \right) \right\rbrack \right\} \\ - 2\pi r\left( \text{NR} \right) \Delta z \left( j \right)\left( h_{\text{b}} + \varepsilon\sigma h_{\text{r}} \right)\left\{ \theta_{1}\ \left\lbrack T_{1}\left( \text{NE}'' \right) - T_{1}\left( \text{NT} \right) \right\rbrack \right.\ \\ + \theta_{2}\ \left. \ \left\lbrack T_{2}\left( \text{NE}'' \right) - T_{2}\left( \text{NT} \right) \right\rbrack\ \right\} + Q\left( \text{NE}'' \right) \\ \end{matrix}\end{split}\]

where

\(c_{\text{e}}\) = cladding heat capacity

(3.3‑33)

\[m_{\text{e}} = \text{cladding mass} = 2\pi\rho_{\text{e}}\left\lbrack r\left( \mathrm{\text{NE}}' \right)^{2} - r\left( \mathrm{\text{NE}} \right)^{2} \right\rbrack \Delta z (j)\]

\(p_\text{e}\) = cladding density

and

(3.3‑34)

\[{\overline{r}}_{\text{NE}} = r\ \left( \text{NE} \right) + \frac{1}{4}\left\lbrack r \ \left( \text{NE}' \right) - r\ \left( \text{NE} \right) \right\rbrack\]

Note that the factors of 4 in Eqs. 3.3-32 and 3.3-34 come about because the inner cladding node represents one fourth of the thickness of the cladding.

3.3.1.2.5. Cladding Mid-point, Node NE

For the cladding mid-point node, Eq. 3.3-1 becomes

(3.3‑35)

\[\begin{split}\begin{matrix} \frac{m_{\text{e}}c_{\text{e}}}{2}\frac{T_{2}\left( \text{NE} \right) - T_{1}(\text{NE})}{ \Delta t } \\ = \frac{2\pi{\overline{r}}_{\text{NE}'} \Delta z (j){\overline{k}}_{\text{NE,NE}'}}{\Delta r_{\text{NE,NE}'}} \left\{ \theta_{1}\left\lbrack T_{1}\left( \text{NE}' \right) - T_{1}(\text{NE}) \right\rbrack + \theta_{2}\left\lbrack T_{2}\left( \text{NE}' \right) - T_{2}(\text{NE}) \right\rbrack \right\} \\ - \frac{2\pi{\overline{r}}_{\text{NE}} \Delta z (j){\overline{k}}_{\text{NE}''\text{,NE}}}{\Delta r_{\text{NE}''\text{,NE}}} \left\{ \theta_{1}\left\lbrack T_{1}\left( \text{NE} \right) - T_{1}(\text{NE}'') \right\rbrack + \theta_{2}\left\lbrack T_{2}\left( \text{NE} \right) - T_{2}(\text{NE}'') \right \rbrack \right \} + Q(\text{NE}) \\ \end{matrix}\end{split}\]

where

(3.3‑36)

\[{\overline{r}}_{\text{NE}'} = r\ \left( \text{NE} \right) + \frac{3}{4}\left\lbrack r \left( \text{NE}' \right) - r\ \left( \text{NE} \right) \right\rbrack\]

3.3.1.2.6. Cladding Outer Node, Node \(\text{NE}'\)

The out cladding node transfers heat to both the cladding mid-point node and the coolant node, so the equation for the outer cladding node temperature is

(3.3‑37)

\[\begin{split}\begin{matrix} \frac{m_{\text{e}}c_{\text{e}}}{4}\frac{T_{2}\left( \text{NE}' \right) - T_{1}(\text{NE}')}{ \Delta t } \\ = - \frac{2\pi{\overline{r}}_{\text{NE}'} \Delta z (j){\overline{k}}_{\text{NE,NE}'}}{{\overline{r}}_{\text{NE,NE}'}}\ \left\{ \theta_{1}\left\lbrack T_{1}\left( \text{NE}' \right) - T_{1}(\text{NE}) \right\rbrack + \theta_{2}\left\lbrack T_{2}\left( \text{NE}' \right) - T_{2}(\text{NE}) \right\rbrack \right\} \\ + 2 \pi r \left( \text{NE}' \right) \Delta z (j)\ \left\{ \theta_{1}h_{\text{c}1}(j)\left\lbrack T_{1}\left( \text{NC} \right) - T_{1}\left( \text{NE}' \right) \right\rbrack + \theta_{2}h_{\text{c}2}(j)\left\lbrack T_{2}\left( \text{NC} \right) - T_{2} \left( \text{NE}' \right) \right \rbrack \right\} + Q(\text{NE}') \\ \end{matrix}\end{split}\]

Note that \(T(\text{NC}) = {\overline{T}}_{c}\left( jc \right)\). Also, \(hc_1\) and \(hc_2\) are the coolant heat-transfer coefficients at \(t \text{ and } t + \Delta t\) as calculated from Eq. 3.3-9,

3.3.1.2.7. Coolant, Node NC

Coolant temperatures are calculated for the whole length of the subassembly, whereas fuel temperatures are computed in the core and blankets only. Therefore, the axial coolant node mesh extends beyond the fuel mesh; and the coolant axial node index, \(jc\), is related to the fuel axial node index, \(j\), by

(3.3‑38)

\[jc = j + j_{\text{cblbt}} - 1\]

where \(j_{\text{cblbt}}\) is the coolant node at the bottom of the lower blanket. In the \(T_1 (i,j)\) and \(T_2 (i,j)\) arrays, the coolant node corresponds to

(3.3‑39)

\[T_{2}\left( \text{NC,j} \right) = \overline{T}_{\text{c}}\left( jc \right)\]

In the non-voiding case, the coolant flow is usually upward. In such a situation, the transient calculation for a time step starts at the subassembly inlet and works upward through the lower reflector zones, through the pin section, and finally through the upper reflector zones. The code can also handle downward coolant flow during the transient, although the initial steady-state coolant flows must all be upward. In the downward situation, the calculation starts at the top of the subassembly and works down to the inlet.

In the core and blanket regions, Eq. 3.3-5 becomes

(3.3‑40)

\[\begin{split} \begin{matrix} {\overline{\rho}}_{\text{c}}\left( jc \right){\overline{c}}_{\text{c}}\left( jc \right)\frac{T_{2}\left( \text{NC} \right) - T_{1}\left( \text{NC} \right)}{\Delta t} + \frac{2{\overline{c}}_{\text{c}}\left( jc \right)}{\Delta z\left( j \right)A_{\text{c}}\left( jc \right)}\ \left\{ \theta_{1}\left| w_{1} \right| \left\lbrack T_{1}\left( \text{NC} \right) - {T'}_{1} \right\rbrack \\ + \theta_{2}\left| w_{2} \right| \left\lbrack T_{2}\ \left( \text{NC} \right) - {T'}_{2} \right\rbrack\ \right\} = \frac{Q\left( \text{NC} \right)}{A_{\text{c}}\left( jc \right)\Delta z\left( j \right)} + \frac{2\pi r\left( NE' \right)}{A_{\text{c}}\left( jc \right)} \\ \left\{ \theta_{1}\ h_{\text{c}1}\left( j \right) \left\lbrack T_{1}\left( \text{NE}' \right) - T_{1}\left( \text{NC} \right) \right\rbrack + \theta_{2}h_{\text{c}2}\left( j \right)\left\lbrack T_{2}\ \left( NE' \right) - T_{2}\left( \text{NE} \right) \right\rbrack \right\} \\ + \frac{S_{\text{pr}}}{A_{\text{c}}\left( jc \right)}\left\{ \theta_{1}\ H_{\text{sic}1}\left( jc \right) \left\lbrack T_{1}\left( \text{NSI} \right) - T_{1}\left( \text{NC} \right) \right\rbrack \\ + \theta_{2}\ H_{\text{sic}2}\left( jc \right) \left\lbrack T_{2}\left( \text{NSI} \right) - T_{2}\left( \text{NC} \right) \right\rbrack \right\} \\ \end{matrix}\end{split}\]

where

S_pr = structure perimeter

w₁ and w₂ = the coolant mass flow rates (kg/s) at t and \(t + t\)

NSI = the inner structure node

(3.3‑41a-b)

\[\begin{split} {T'}_{1} = \begin{cases} T_{\text{c}1} \left( jc \right) & \text{if}\ w_{1} \geq 0 \\ T_{\text{c}} \left( jc + 1 \right) & \text{if}\ w_{1} < \ 0 \\ \end{cases}\end{split}\]

(3.3‑42a-b)

\[\begin{split} {T'}_{2} = \begin{cases} T_{\text{c}2} \left( jc \right) & \text{if}\ w_{2} \geq 0 \\ T_{\text{c}} \left( jc + 1 \right) & \text{if}\ w_{2} < \ 0 \\ \end{cases}\end{split}\]

and

H_sic = the heat-transfer coefficient from the structure inner node to the coolant

(3.3‑43)

\[H_{\text{sic}} = \frac{2h_{\text{c}} k_{\text{si}}}{2k_{\text{si}} + h_{\text{c}} d_{\text{sti}}}\]

Note that Eq. 3.3-43 is obtained by adding thermal resistance in series:

(3.3‑44)

\[\frac{1}{H_{\text{sic}}} = \frac{1}{h_{\text{c}}} + \frac{d_{\text{sti}}}{2k_{\text{si}}}\]

3.3.1.2.8. Structure Inner Node, Node NSI

In the core and blanket regions,

(3.3‑45)

\[\begin{split} \begin{matrix} \left( \rho c \right)_{\text{sti}}d_{\text{sti}}\frac{T_{2}\left( \text{NSI} \right) - T_{1}\left( \text{NSI} \right)}{\Delta t} = \theta_{1}H_{\text{sic}1}\left( jc \right)\left\lbrack T_{1} \left( \text{NC} \right) - T_{1}\left( \text{NSI} \right) \right\rbrack \\ +\theta_{2}\ H_{sic2}\left( jc \right)\left\lbrack T_{2}\ \left( \text{NC} \right) - T_{2}\left( \text{NSI} \right) \right\rbrack \\ + H_{\text{stio}}\left( jc \right) \left\{\theta_{1} \left\lbrack T_{1}\left( \text{NSO} \right) - T_{1}\left( \text{NSI} \right) \right\rbrack \\ + \theta_{2}\left\lbrack T_{2} \left( \text{NSO} \right) - T_{2}\left( \text{NSI} \right) \right\rbrack \right\} + Q_{\text{st}}\frac{d_{\text{sti}}}{d_{\text{sti}} + d_{\text{sto}}} \\ \end{matrix}\end{split}\]

where

NSO = outer structure node

\(d_{\text{sti}}\) = thickness of inner structure node

\(d_{\text{sto}}\) = thickness of outer structure node

(3.3‑46)

\[H_{\text{stio}} = \frac{2k_{\text{si}}k_{\text{so}}}{d_{\text{sti}}k_{\text{so}} + d_{\text{sto}}k_{\text{si}}}\]

\(k_{\text{si}}\) = thermal conductivity of the inner structure node

\(k_{\text{so}}\) = thermal conductivity of the outer structure node

and

\(Q_{\text{st}} = \frac{\gamma_{\text{s}}\overline{P}(j)}{S_{\text{pr}} \Delta z(j)}\) = direct heating source in the structure.

The left-hand side of Eq. 3.3-45 represents the change in internal energy in the node. The terms on the right-hand side represent heat flow from the coolant and the outer structure node, as well as direct heating of the structure by neutrons and gamma rays. It is assumed that the direct heating source is divided between the inner and outer nodes in proportion to their thicknesses.

3.3.1.2.9. Structure Outer Node, Node NSO

In the core and blankets,

(3.3‑47)

\[\begin{split}\begin{matrix} \left( \rho c \right)_{\text{sto}}d_{\text{sto}}\frac{T_{2}\left( \mathrm{\text{NSO}} \right) - T_{1}(\mathrm{\text{NSO}})}{ \Delta t } = H_{\text{stio}}\left( jc \right)\left\{ \theta_{1}\left\lbrack T_{1}\left( \mathrm{\text{NSI}} \right) - T_{1}\left( \mathrm{\text{NSO}} \right) \right\rbrack \\ + \theta_{2}\left\lbrack T_{2}\left( \mathrm{\text{NSI}} \right) - T_{2}(\mathrm{\text{NSO}}) \right\rbrack \right\} + Q_{\text{st}}\left( jc \right)\frac{d_{\text{sto}}}{d_{\text{sti}} + d_{\text{sto}}} + \frac{Q_{\text{chch}}(jc)}{S_{\text{pr}}} \\ \end{matrix}\end{split}\]

where

\(Q_{\text{chch}} = Q_{\text{chch},\text{I}}\) = subassembly-to-subassembly linear heat transfer rate.

The values used for \(Q_{\text{chch}}\) are discussed in Section 3.11.

3.3.1.2.10. Solution of Finite Difference Equations

Equations 3.3-16, 3.3-27, 3.3-31, 3.3-32, 3.3-35, 3.3-37, 3.3-40, 3.3-45, and 3.3-47 can be written in matrix form, yielding a tri-diagonal matrix of the form

(3.3‑48)

\[\begin{split}\left\lbrack \begin{matrix} \alpha_{1} + \beta_{1} \\ - \beta_{1} \\ 0 \\ \ \ \ \ \ \ \ \ . \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ . \\ \\ \\ \\ \\ 0 \\ 0 \\ \end{matrix}\begin{matrix} \\ \\ \\ \\ \\ . \\ \ \ \ \ \ . \\ \\ \\ \\ \\ \end{matrix}\begin{matrix} - \beta_{1} \\ \alpha_{2} + \beta_{1} + \beta_{2} \\ - \beta_{2} \\ \\ \\ \\ \\ .\ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ .\ \ \ \ \ \\ ...0 \\ .... \\ \end{matrix}\begin{matrix} 0 \\ - \beta_{2} \\ \alpha_{3} + \beta_{2} + \beta_{3} \\ \\ \\ \\ \\ \\ \\ - \beta_{\mathrm{\text{NC}}} \\ 0 \\ \end{matrix}\begin{matrix} 0 \\ 0 \\ - \beta_{2} \\ \\ \\ \\ \\ \\ \\ \alpha_{\mathrm{\text{NSI}}} + \beta_{\mathrm{\text{NC}}} + \beta_{\mathrm{\text{NSI}}} \\ - \beta_{\mathrm{\text{NSI}}} \\ \end{matrix}\begin{matrix} \ldots \\ \ldots \\ \ldots \\ \\ \\ \\ \\ \\ \\ - \beta_{\mathrm{\text{NSI}}} \\ \alpha_{\mathrm{\text{NSO}}} + \beta_{\mathrm{\text{NSI}}} + \beta_{\mathrm{\text{NSO}}} \\ \end{matrix} \right\rbrack\ \begin{bmatrix} T_{2}(1) \\ T_{2}(2) \\ T_{2}(3) \\ \\ \\ \\ \\ \\ \\ T_{2}(\mathrm{\text{NSI}}) \\ T_{2}(\mathrm{\text{NSO}}) \\ \end{bmatrix} = \begin{bmatrix} D_{1} \\ D_{2} \\ D_{3} \\ \\ \\ \\ \\ \\ \\ D_{\mathrm{\text{NSI}}} \\ D_{\mathrm{\text{NSO}}} \\ \end{bmatrix}\end{split}\]

where

(3.3‑49a)

\[\alpha_{1} = \frac{M_{\text{f}}\left( i \right){\overline{c}}_{\text{f}}\left( i \right)}{2\pi\Delta z\left( j \right)}\ \ \ \ \ \text{for}\ \ i\ \ = \ \ 1,...\ \ \text{NT}\]

(3.3‑49b)

\[\alpha_{\text{NE}''} = \frac{M_{\text{e}}c_{\text{e}}}{8\pi\Delta z \left( j \right)}\]

(3.3‑49c)

\[\alpha_{\text{NE}} = \frac{M_{\text{e}}c_{\text{e}}}{4\pi\Delta z\left( j \right)}\ = 2\alpha_{\text{NE}''}\]

(3.3‑49d)

\[\alpha_{\text{NE}'} = \alpha_{\text{NE}''}\]

(3.3‑49e)

\[\alpha_{\text{NC}} = \frac{{\overline{\rho}}_{\text{c}}\left( jc \right){\overline{c}}_{\text{c}}\left( jc \right)A_{\text{c}}\left( jc \right)}{2\pi} + \frac{{\overline{c}}_{\text{c}}\left( jc \right)}{\pi \Delta z\left( jc \right)}\theta_{2} | w_{2} | \Delta t\]

(3.3‑49f)

\[\alpha_{\text{NSI}} = \frac{\left( \rho c \right)_{\text{sti}}d_{\text{sti}}S_{\text{pr}}}{2\pi}\]

(3.3‑49g)

\[\alpha_{\text{NSO}} = \frac{\left( \rho c \right)_{\text{sto}}d_{\text{sto}}S_{\text{pr}}}{2\pi}\]

(3.3‑50a)

\[\beta_{\text{i}} = \frac{r\left( i + 1 \right){\overline{k}}_{\text{i,i} + 1}}{\Delta r_{\text{i,i} + 1}}\theta_{2}\ \Delta t\ \ \ \ \ \ \text{for}\ \ i\ \ = \ \ 1,....NN\]

(3.3‑50b)

\[\beta_{\text{NT}} = r\left( \text{NR} \right)\theta_{2}\ \left\lbrack h_{b} + \varepsilon\sigma h_{\text{r}} \right\rbrack\Delta t\]

(3.3‑50c)

\[\beta_{\text{NE}''} = \frac{\overline{r}_{\text{NE}}\ \overline{k}_{\text{NE}''\text{,NE}}\ }{\Delta r_{\text{NE}''\text{,NE}}}\theta_{2}\Delta t\]

(3.3‑50d)

\[\beta_{\text{NE}} = \frac{\overline{r}_{\text{NE}'}\ \overline{k}_{\text{NE,NE}'}\ }{\Delta r_{\text{NE,NE}'}}\theta_{2} \Delta t\]

(3.3‑50e)

\[\beta_{\text{NE}'} = r_{\text{NE}'}\ h_{c2}\left( j \right)\theta_{2} \Delta t\]

(3.3‑50f)

\[\beta_{\text{NC}} = \frac{S_{\text{pr}}\ }{2\ \pi}H_{\text{sic2}}\left( jc \right)\ \theta_{2} \Delta t\]

(3.3‑50g)

\[\beta_{\text{NSI}} = \frac{S_{\text{pr}}\ }{2\ \pi}H_{\text{stio}}\left( jc \right)\ \theta_{2} \Delta t\]

(3.3‑50h)

\[\beta_{\text{NSO}} = 0\]

(3.3‑51a)

\[D_{1} = T_{1}\left( 1 \right)\left\lbrack \alpha_{1} - \frac{\theta_{1}}{\theta_{2}}\beta_{1} \right\rbrack + \frac{\theta_{1}}{\theta_{2}}\beta_{1}T_{1}\left( 2 \right) + \psi_{1}\]

(3.3‑51b)

\[\begin{split} \begin{matrix} D_{\text{i}} = \frac{\theta_{1}}{\theta_{2}}\beta_{\text{i} - 1}T_{1}\left( i - 1 \right) + T_{1}\left( i \right)\left\lbrack \alpha_{1} - \frac{\theta_{1}}{\theta_{2}}\left( \beta_{\text{i} - 1} + \beta_{\text{i}} \right) \right\rbrack \\ + \frac{\theta_{1}}{\theta_{2}}\beta_{\text{i}}T_{1}\left( i + 1 \right) + \psi_{1}\ \ \ \ \ \ \ \text{for}\ \ i = 2,...,\ NSI \\ \end{matrix}\end{split}\]

(3.3‑51c)

\[D_{\text{NSO}} = \frac{\theta_{1}}{\theta_{2}}\beta_{\text{NSI}}T_{1}\left( \text{NSI} \right) + T_{1}\left( \text{NSO} \right)\left\lbrack \alpha_{\text{NSO}} - \frac{\theta_{1}}{\theta_{2}}\left( \beta_{\text{NSI}} + \beta_{\text{NSO}} \right) \right\rbrack + \psi_{\text{NSO}}\]

(3.3‑52a)

\[\psi_{\text{i}} = \frac{Q\left( i \right) \Delta t }{2\pi\Delta z\left( j \right)}\ \ \text{for}\ \ i = 1,...,\ \ \text{NE}'\]

(3.3‑52b)

\[\psi_{\text{NC}} = \frac{Q\left( \text{NC} \right) \Delta t }{2\pi\Delta z\left( j \right)}\ + \frac{{\overline{c}}_{\text{c}}\left( jc \right)\Delta t}{\pi \Delta z\left( j \right)}\left\lbrack \theta_{1}\left| w_{1} \right|{T'}_{1} + \theta_{2}\left| w_{2} \right|{T'}_{2} \right\rbrack\]

(3.3‑52c)

\[\psi_{\text{NSI}} = \frac{Q\left( \mathrm{\text{NSI}} \right) \Delta t }{2\pi\Delta z(j)}\]

and

(3.3‑52d)

\[\psi_{\text{NSO}} = \frac{Q\left( \text{NSO} \right) \Delta t }{2\pi\Delta z\left( j \right)} + \frac{1}{2\pi}Q_{\text{chch}}\Delta t\]

In these equations the \(\alpha\) array is related to heat capacity, the \(\beta\) array is related to heat transfer between adjacent nodes, and the \(\psi\) array is related to the heat source.

The matrix equations 3.3-49 are solved by Gaussian elimination. First arrays \(A_i\) and \(S_i\) are defined:

(3.3‑53)

\[A_{\text{i}} = \alpha_{\text{i}} + \beta_{\text{i}} + \beta_{\text{i} = 1} - \frac{\beta_{\text{i} - 1}^{2}}{A_{\text{i} - 1}}\ \ \ \ \ \text{for}\ \ i = 2,...,\ \ NSO\]

(3.3‑54a)

\[S_{1} = D_{1}\]

and

(3.3‑54b)

\[S_{\text{i}} = D_{\text{i}} + \frac{\beta_{\text{i} - 1}S_{\text{i} - 1}}{A_{\text{i} - 1}}\ \ \ \ \ \text{for}\ \ i = 2,...,\ \ NSO\]

Then,

(3.3‑55a)

\[T_{2}\left( \text{NSO} \right) = \frac{S_{\text{NSO}}}{A_{\text{NSO}}}\]

and

(3.3‑55b)

\[T_{2}\left( i \right) = S_{\text{i}} + \frac{\beta_{\text{i}}}{A_{\text{i}}}T_{2}\left( i + 1 \right)\ \ \ \ \text{for}\ \ i = NSI,\ \ NC,...,\ \ 1\]

3.3.2. Reflector Zones

In reflector zones, a two-node slab geometry treatment is used at each axial node for heat transfer to the “reflector”. The reflector represents any material in the subassembly outside the pin section.

Typically, this material includes shield orifice blocks near the subassembly inlet, and instrumentation in the upper part of the subassembly. Usually, this material does not come to the form of either pure slabs or pure cylinders, and so any simple geometrical treatment of it will be only an approximation. The best that one is likely to do with a simple heat-transfer calculation is to use a slab calculation with parameters chosen to match total heat capacity, total heat-transfer surface area, and the approximate effective thickness of the material.

3.3.2.1. Basic Equations

The basic equations used for coolant and structure temperatures in reflector zones are the same as Eqs. 3.3-5 and 3.3-10 used in the core and blanket regions, except that no heat generation is considered in the reflector zones. Therefore, the \(Q_{\text{c}}\), term of Eq. 3.3-5 and the \(Q\) term of Eq. 3.3-10 are eliminated in the reflector zones. The reflector is treated with a one-dimensional heat conduction equation that is the same as the one used for the structure, except that the thermal properties \(\rho\), \(c\), and \(k\) used for the reflector can be different from those used for the structure.

3.3.2.2. Finite Difference Equations

Figure 3.2.6 shows the radial mesh structures used for an axial node in a reflector region.

3.3.2.2.1. Reflector Inner Node

Equation 3.3-10 becomes

(3.3‑56)

\[\begin{split} \begin{matrix} \left( \rho c \right)_{\text{r}}d_{\text{ri}}\frac{T_{\text{ri}2}\left( jc \right) - T_{\text{ri}1}\left( jc \right)}{\Delta t} = H_{\text{rio}}\left( jc \right)\ \left\{ \theta_{1}\ \left\lbrack T_{\text{ro}1}\left( jc \right) - T_{\text{ri}1}\left( jc \right) \right\rbrack \right. \\ \left. + \theta_{2}\left\lbrack T_{\text{ro}2}\left( jc \right) - T_{\text{ri}2}\left( jc \right) \right\rbrack \right\} \\ \end{matrix}\end{split}\]

where

\(\rho c_{\text{r}}\) = density times specific heat of the reflector

\(d_{\text{ri}}\) = thickness of inner node

\(T_{\text{ri}1},~ T_{\text{ri}2}\) = reflector inner node temperature at the beginning and end of the time step

\(T_{\text{ro}},~ T_{\text{ro}2}\) = reflector outer node temperature at the beginning and end of the t ime step

\(d_{\text{ro}}\) = thickness of outer reflector node

and

(3.3‑57)

\[H_{\text{rio}} = \frac{2k_{\text{r}}}{d_{\text{ri}} + d_{\text{ro}}}\]

Equation 3.3-57 is obtained by adding thermal resistances in series:

(3.3‑58)

\[\frac{1}{H_{\text{rio}}} = \frac{d_{\text{ri}}}{2k_{\text{r}}} + \frac{d_{\text{ro}}}{2k_{\text{r}}}\]

Equation 3.3-56 is similar to Eq. 3.3-47 for the outer structure node, except there is no direct heating source in the reflectors.

3.3.2.2.2. Reflector Outer Node

The equation for the reflector outer node temperature is similar to Eq. 3.3-45 for the structure inner node:

(3.3‑59)

\[\begin{split} \begin{matrix} \left( \rho c \right)_{\text{r}}d_{\text{ro}}\frac{T_{\text{ro}2}\left( jc \right) - T_{\text{ro}1}\left( jc \right)}{\Delta t} \\ = \theta_{1}H_{\text{erc}1}\left( jc \right)\left\lbrack {\overline{T}}_{\text{c}1}\left( jc \right) - T_{\text{ro}1}\left( jc \right) \right\rbrack + \theta_{2}H_{\text{erc}2}\left( jc \right)\left\lbrack {\overline{T}}_{\text{c}2}\left( jc \right) - T_{\text{ro}2}\left( jc \right) \right\rbrack \\ + H_{\text{rio}}\left( jc \right)\left\{ \theta_{1}\left\lbrack T_{\text{ri}1}\left( jc \right) - T_{\text{ro}1}\left( jc \right) \right\rbrack + \theta_{2}\left\lbrack T_{\text{ri}2}\left( jc \right) - T_{\text{ro}2}\left( jc \right) \right\rbrack \right\} \\ \end{matrix}\end{split}\]

where

(3.3‑60)

\[H_{\text{erc}} = \frac{h_{\text{c}}k_{\text{r}}}{k_{\text{r}} + \frac{h_{\text{c}}d_{\text{ro}}}{2}}\]

Note that

(3.3‑61)

\[{\overline{T}}_{\text{c}}\left( jc \right) = \left\lbrack \ T_{\text{c}}\left( jc \right) + T_{\text{c}}\left( jc + 1 \right) \right\rbrack\ /\ 2\]

3.3.2.2.3. Coolant Node

In the reflector zones and in the gas plenum, Eq. 3.3-5 becomes

(3.3‑62)

\[\begin{split} \begin{matrix} {\overline{\rho}}_{\text{c}}\left( jc \right){\overline{c}}_{\text{c}}\left( jc \right)\frac{{\overline{T}}_{\text{c}2}\left( jc \right) - T_{\text{c}1}\left( jc \right)}{\Delta t} + \frac{2{\overline{c}}_{\text{c}}\left( jc \right)}{\Delta z\left( jc \right)A_{\text{c}}\left( jc \right)}\left\{ \theta_{1}\left| w_{1} \right|\left\lbrack {\overline{T}}_{\text{c}}\left( jc \right) - {T'}_{1} \right\rbrack \right. \\ \left. + \theta_{2}\left| w_{2} \right|\left\lbrack {\overline{T}}_{\text{c}2}\left( jc \right) - {T'}_{2} \right\rbrack\ \right\} \\ = \ \frac{S_{\text{er}}\left( \text{KZ} \right)}{A_{\text{c}}\left( jc \right)}\left\{ \theta_{1}H_{\text{erc}1}\left\lbrack T_{\text{er}1}\left( jc \right) - T_{\text{c}1}\left( jc \right)\ \right\rbrack \right. \\ \left. + \theta_{2}H_{\text{erc}2}\left\lbrack T_{\text{er}2}\left( jc \right) - {\overline{T}}_{\text{c}2}\left( jc \right) \right\rbrack\ \right\} + \frac{S_{\text{pr}}}{A_{\text{c}}\left( jc \right)}\ \left\{ \theta_{1}H_{\text{sic}1}\left\lbrack T_{\text{ri}1}\left( jc \right) \right.\ \right. \\ \left. \ \left. \ - T_{\text{c}1}\left( jc \right) \right\rbrack + \theta_{2}H_{\text{sci}2}\left( jc \right)\left\lbrack T_{\text{sti}2}\left( jc \right) - {\overline{T}}_{\text{c}2}\left( jc \right) \right\rbrack \right\} \\ \end{matrix}\end{split}\]

where, in reflector zones,

\(T_{\text{er}1}\) = \(T_{\text{ro}1}\)

\(T_{\text{er}2}\) = \(T_{\text{ro}2}\)

\(S_{\text{er}}\) = \(S_{\text{r}}\) = reflector perimeter

\(S_{\text{pr}}\) = structure perimeter

and

\(T_{\text{sti}}\) = structure inner node temperature

3.3.2.2.4. Structure Nodes

The finite difference approximation to Eq. 3.3-10 for the structure nodes is the same as in the core and blanket regions. Equations 3.3-45 and 3.3-47 are used, except that \(Q_{\text{st}}\) is zero outside the core and blankets.

3.3.2.3. Solution of Finite Difference Equations

(3.3‑63)

\[\begin{split}\begin{bmatrix} \alpha_{1} + \beta_{1} & - \beta_{1} & 0 & 0 & 0 \\ - \beta_{1} & \alpha_{2} + \beta_{1} + \beta_{2} & - \beta_{2} & 0 & 0 \\ 0 & - \beta_{2} & \alpha_{3} + \beta_{2} + \beta_{3} & - \beta_{3} & 0 \\ 0 & 0 & - \beta_{3} & \alpha_{4} + \beta_{3} + \beta_{4} & - \beta_{4} \\ 0 & 0 & 0 & - \beta_{4} & \alpha_{5} + \beta_{4} + \beta_{5} \\ \end{bmatrix}\begin{bmatrix} T_{ri2} \\ T_{ro2} \\ {\overline{T}}_{c2} \\ T_{Sti2} \\ T_{St02} \\ \end{bmatrix} = \begin{bmatrix} D_{1} \\ D_{2} \\ D_{3} \\ D_{4} \\ D_{5} \\ \end{bmatrix}\end{split}\]

where

(3.3‑64a)

\[\alpha_{1} = \left( \rho c \right)_{\text{r}}d_{\text{ri}}S_{\text{er}}\left( \text{KZ} \right)\]

(3.3‑64b)

\[\alpha_{2} = \left( \rho c \right)_{\text{r}}d_{\text{ro}}S_{\text{er}}\left( \text{KZ} \right)\]

(3.3‑64c)

\[\alpha_{3} = {\overline{\rho}}_{\text{c}}\ {\overline{c}}_{e}\ A_{\text{c}} + 2\ \ {\overline{c}}_{\text{c}}\ \theta_{2}\left| w_{2} \right| \Delta t\]

(3.3‑64d)

\[\alpha_{4} = \left( \rho c \right)_{\text{sti}}d_{\text{sti}}S_{\text{pr}}\]

(3.3‑64e)

\[\alpha_{5} = \left( \rho c \right)_{\text{sto}}d_{\text{sto}}S_{\text{pr}}\]

(3.3‑65a)

\[\beta_{1} = \theta_{2}H_{\text{rio}}\left( jc \right)S_{\text{er}} \Delta t\]

(3.3‑65b)

\[\beta_{2} = \theta_{2}H_{\text{erc}2}\left( jc \right)S_{\text{er}} \Delta t\]

(3.3‑65c)

\[\beta_{3} = \theta_{2}H_{\text{sic}2}\left( jc \right)S_{\text{pr}} \Delta t\]

(3.3‑65d)

\[\beta_{4} = \theta_{2}H_{\text{stio}}\left( jc \right)S_{\text{pr}} \Delta t\]

(3.3‑65e)

\[\beta_{5} = \theta\]

(3.3‑66a)

\[D_{1} = T_{\text{ri}1}\ \left\lbrack \alpha_{1} - \frac{\theta_{1}}{\theta_{2}} \beta_{1} \right\rbrack + \frac{\theta_{1}}{\theta_{2}}\ \beta_{1}\ T_{\text{ro}1}\]

(3.3‑66b)

\[\begin{split} \begin{matrix} D_{\text{i}} = \frac{\theta_{1}}{\theta_{2}}\ \beta_{\text{i} - 1}{T''}_{1}\left( \text{i} - 1 \right) + {T''}_{1}\left( i \right) \left\lbrack \alpha_{1} - \frac{\theta_{1}}{\theta_{2}} \left( \beta_{\text{i} - 1} + \beta_{1} \right) \right\rbrack \\ + \frac{\theta_{1}}{\theta_{2}} \beta_{\text{i}}{T''}_{1}\left( i + 1 \right)\ \ \ \ \ \text{for}\ \ i = 2,\ \ 4 \\ \end{matrix}\end{split}\]

(3.3‑66c)

\[\begin{split} \begin{matrix} D_{3} = \frac{\theta_{1}}{\theta_{2}} \beta_{2}{T''}_{1}\left( 2 \right) + {T''}_{1}\left( 3 \right) \left\lbrack \alpha_{3} - \frac{\theta_{1}}{\theta_{2}} \left( \beta_{2} + \beta_{3} \right) \right\rbrack + \frac{\theta_{1}}{\theta_{2}} \beta_{3}{T''}_{1}\left( 4 \right) \\ + 2 \frac{{\overline{c}}_{c}\Delta t}{\Delta z} \left\lbrack \theta_{1}\left| w_{1} \right|{T'}_{1} + \theta_{2}\left| w_{2} \right| {T'}_{2} \right\rbrack \\ \end{matrix}\end{split}\]

(3.3‑66d)

\[D_{5} = \frac{\theta_{1}}{\theta_{2}} \beta_{4}{T''}_{1}\left( 4 \right) + {T''}_{1}\left( 5 \right) \left\lbrack \alpha_{5} - \frac{\theta_{1}}{\theta_{2}} \left( \beta_{4} + \beta_{5} \right) \right\rbrack + S_{\text{pr}}\ Q_{\text{chch}}\Delta t\]

(3.3‑67a)

\[{T''}_{1}\left( 1 \right)\ \ = \ \ T_{\text{ri}1}\left( jc \right)\]

(3.3‑67b)

\[{T''}_{1}\left( 2 \right)\ \ = \ \ T_{\text{ro}1}\left( jc \right)\]

(3.3‑67c)

\[{T''}_{1}\left( 3 \right)\ \ = \ \ {\overline{T}}_{\text{c}1}\left( jc \right)\]

(3.3‑67d)

\[{T''}_{1}\left( 4 \right)\ \ = \ \ T_{\text{sti}1}\left( jc \right)\]

and

(3.3‑67e)

\[{T''}_{1}\left( 5 \right)\ \ = \ \ T_{\text{sto}1}\left( jc \right)\]

This tri-diagonal matrix is solved in the same manner as in Section 3.3.1.2 above.

3.3.3. Gas Plenum Region

In the gas plenum region, a single gas node is in contact with all axial cladding nodes. A single radial node is used in the cladding, as indicated in Figure 3.2.5.

3.3.3.1. Basic Equations

The basic equations used in the cladding, coolant, and structure in the gas plenum region are the same as those used in the core and blankets, except that there is no heat source term outside of the core and blankets. The gas is assumed to transfer heat only to the cladding, and the basic equation used for the gas temperature is

(3.3‑68)

\[\left( z_{\text{pt}} - z_{\text{pb}} \right) (\rho c)_{\text{g}} A_{\text{g}} \frac{\text{dT}_{\text{g}}}{\text{dt}} = 2 \pi r_{\text{brp}} H_{\text{eg}} \int_{z_{\text{pb}}}^{z_{\text{pt}}} \left( T_{\text{e}} - T_{\text{g}} \right) \text{dz}\]

where

\(z_{\text{pb}}\) = elevation at the bottom of the gas plenum

\(z_{\text{pt}}\) = elevation at the top of the gas plenum

\((\rho c)_{\text{g}}\) = density times specific heat for the plenum gas

\(A_{\text{g}}\) = cross sectional area of the gas plenum

(3.3‑69)

\[A_{\text{g}} = \pi r^2_{\text{brp}}\]

\(r_{\text{brp}}\) = cladding inner radius in the gas plenum region

\(T_{\text{g}}\) = gas temperature

\(H_{\text{eg}}\) = heat-transfer coefficient from the plenum gas to the cladding node

\(T_{\text{e}}\) = cladding temperature

3.3.3.2. Finite Difference Equations

3.3.3.2.1. Gas Plenum

Equation 3.3-69 becomes

(3.3‑70)

\[\begin{split} \begin{matrix} \left( \rho c \right)_{\text{g}}A_{\text{g}}\frac{\left( T_{\text{g}2} - T_{\text{g}1} \right)}{\Delta t} \\ = 2\pi r_{\text{brp}}H_{\text{eg}}\frac{\sum_{\text{jp}}\left\{ \theta_{1}\left\lbrack T_{\text{e}1}\left( jp \right) - T_{\text{g}1} \right\rbrack + \theta_{2}\left\lbrack T_{\text{e}2}\left( jp \right) - T_{\text{g}2} \right\rbrack \right\}\Delta z\left( jp \right)}{\sum_{\text{jp}}{\Delta z\left( jp \right)}} \\ \end{matrix}\end{split}\]

where

\(jp\) = plenum node

\(T_{\text{g}1}\) = plenum gas temperature at the beginning of the time step

\(T_{\text{g}2}\) = plenum gas temperature at the end of the time step

(3.3‑71)

\[H_{\text{eg}} = \frac{1}{R_{\text{g}} + \frac{r_{\text{erp}} - r_{\text{brp}}}{2k_{\text{ep}}}} = \frac{2k_{\text{ep}}}{r_{\text{erp}} - r_{\text{brp}} + 2k_{\text{ep}}R_{\text{g}}}\]

\(k_{\text{ep}}\) = cladding thermal conductivity in the gas plenum

and

\(R_{\text{g}}\) = thermal resistance of the gas.

3.3.3.2.2. Cladding Node

The equation for the cladding node is

(3.3‑72)

\[\begin{split} \begin{matrix} \rho_{\text{e}}c_{\text{e}}A_{\text{ep}}\frac{T_{\text{e}2}\left( jp \right) - T_{\text{e}1}\left( jp \right)}{\Delta t} \\ = 2\pi r_{\text{erp}}\left\{\theta_{1} \ H_{\text{erc}1}\left\lbrack {\overline{T}}_{\text{c}1}\left( jc \right) - T_{\text{e}1}\left( jp \right) \right\rbrack \\ + \theta_{2}H_{\text{erc}2}\left\lbrack {\overline{T}}_{\text{c}2}\left( jc \right) - T_{\text{e}2}\left( jp \right) \right\rbrack \right\} + \ 2\pi r_{\text{brp}}H_{\text{eg}}\left\{ \theta_{1} \left\lbrack T_{\text{g}1} - T_{\text{e}1}\left( jp \right) \right\rbrack \\ + \theta_{2} \left\lbrack T_{\text{g}2} - T_{\text{e}2}\left( jp \right) \right\rbrack \right\} \\ \end{matrix}\end{split}\]

where

\(\rho_{\text{e}}\) = cladding density

\(c_{\text{e}}\) = cladding specific heat

(3.3‑73)

\[A_{\text{ep}} = \pi\left\lbrack r_{\text{erp}}^{2} - r_{\text{brp}}^{2}\ \right\rbrack\]

and

\(r_{\text{erp}}\) = cladding outer radius in the gas plenum region

3.3.3.2.3. Coolant Node

The equation for the coolant node in the gas plenum region is the same as Eq. 3.3-62 for reflector zones, except that in the gas plenum

(3.3‑74)

\[H_{\text{erc}} = \frac{h_{\text{e}}k_{\text{e}}}{k_{\text{e}} + \frac{h_{\text{c}}\left( r_{\text{erp}} - r_{\text{brp}} \right)}{2}}\]

(3.3‑75)

\[S_{\text{cr}} = 2\pi r_{\text{erp}}\]

and

\(k_{\text{e}}\) = cladding thermal conductivity.

3.3.3.2.4. Structure Nodes

The finite difference approximations used for the structure in the gas plenum region are the same as those used in the core and blankets. Equations 3.3-45 and 3.3-47 are used, except that \(Q_{\text{st}}\) is zero.

3.3.3.3. Solution of Finite Difference Equations

A direct solution of the finite difference equations would be complicated, since Eq. 3.3-70 connects a number of axial nodes, each containing a number of radial nodes. Instead, an approximate solution method is used. This method uses the assumption that the total heat capacity of the gas is much less than the total heat capacity of the cladding in the gas plenum region, or

(3.3‑76)

\[\left( \rho c \right)_{\text{g}}\ A_{\text{g}}\ < \ \ < \ \ \rho_{\text{e}}\ c_{\text{e}}\ A_{\text{ep}}\]

which should always be the case.

The solution method contains five steps:

1. Set \(T_{\text{g}2}\) = \(T_{\text{g}1}\).

2. Solve Eqs. 3.3-72, 3.3-62, 3.3-45, and 3.3-47 for all axial nodes in the gas plenum to get new cladding, coolant, and structure temperatures.

3. Use Eq. 3.3-70 to obtain a new computed value for \(T_{\text{g}2}\).

4. For each axial node, calculate the heat flow error, \(\Delta E\), due to the assumption in step 1:

(3.3‑77)

\[\Delta E = \left( \rho c \right)_{\text{g}}\ A_{\text{g}}\ \left( T_{\text{g}2} - T_{\text{g}1} \right)\]

1. Add this heat flow to the cladding, changing the cladding temperature:

(3.3‑78)

\[T_{\text{e}2} = T_{\text{c}2} + \frac{\Delta E}{\rho_{\text{e}}c_{\text{e}}A_{\text{ep}}}\]

In step 2, the equations for each axial node give a matrix equation of the form

(3.3‑79)

\[\begin{split} \begin{bmatrix} \alpha_{1} + \beta_{1} & - \beta_{1} & 0 & 0 \\ - \beta_{1} & \alpha_{1} + \beta_{1} + \beta_{2} & - \beta_{2} & 0 \\ 0 & - \beta_{2} & \alpha_{3} + \beta_{2} + \beta_{3} & - \beta_{3} \\ 0 & 0 & - \beta_{3} & \alpha_{4} + \beta_{3} + \beta_{4} \\ \end{bmatrix}\begin{bmatrix} {T''}_{2}\left( 1 \right) \\ {T''}_{2}\left( 2 \right) \\ {T''}_{2}\left( 3 \right) \\ {T''}_{2}\left( 4 \right) \\ \end{bmatrix} = \begin{bmatrix} D_{1} \\ D_{2} \\ D_{3} \\ D_{4} \\ \end{bmatrix}\end{split}\]

where

(3.3‑80a)

\[T_{2}'' \left( 1 \right) = T_{\text{e}2}(jp)\]

(3.3‑80b)

\[T_{2}'' \left( 2 \right) = {\overline{T}}_{c2}(jc)\]

(3.3‑80c)

\[T_{2}'' \left( 3 \right) = T_{\text{sti}2}(jc)\]

(3.3‑80d)

\[T_{2}'' \left( 4 \right) = T_{\text{sto}2}(jc)\]

(3.3‑81a)

\[\alpha_{1} = \rho_{\text{e}} c_{\text{e}} A_{\text{ep}} + 2\pi r_{\text{brp}} \Delta t \theta_{2}\ H_{\text{eg}}\]

(3.3‑81b)

\[\alpha_{2} = {\overline{\rho}}_{\text{e}}{\overline{c}}_{\text{e}}A_{\text{e}} + 2{\overline{c}}_{c}\theta_{2}\ \left| w_{2} \right| \Delta t\]

(3.3‑81c)

\[\alpha_{3} = \left( \rho c \right)_{\text{sti}}\ d_{\text{sti}}\ S_{\text{pr}}\]

(3.3‑81d)

\[\alpha_{4} = \left( \rho c \right)_{\text{sto}}d_{\text{sto}}\ S_{\text{pr}}\]

(3.3‑82a)

\[\beta_{1} = 2\pi\ r_{\text{erp}}\theta_{2}\ H_{\text{erc}2}\ \left( jc \right) \Delta t\]

(3.3‑82b)

\[\beta_{2} = \theta_{2}\ H_{\text{sic}2}\ \left( jc \right)S_{\text{pr}} \Delta t\]

(3.3‑82c)

\[\beta_{3} = \theta_{2}\ H_{\text{stio}2}\ \left( jc \right)S_{\text{pr}} \Delta t\]

(3.3‑82d)

\[\beta_{4} = 0\]

(3.3‑83a)

\[D_{1} = {T''}_{1}\left( 1 \right)\ \left\lbrack \alpha_{1} - \frac{\theta_{1}}{\theta_{2}}\ \beta_{1} \right\rbrack + \frac{\theta_{1}}{\theta_{2}}\ \beta_{1}\ {T''}_{1}\left( 2 \right) + \ 2\pi r_{\text{brp}}\Delta t H_{\text{eg}}\left\lbrack T_{g1} - T_{e1}\left( jp \right) \right\rbrack\]

(3.3‑83b)

\[\begin{split} \begin{matrix} D_{2} = \frac{\theta_{1}}{\theta_{2}}\beta_{1}\ {T''}_{1}\left( 1 \right) + {T''}_{1}\ \left( 2 \right)\ \left\lbrack \alpha_{2} - \frac{\theta_{1}}{\theta_{2}}\ \left( \beta_{1} + \beta_{2} \right) \right\rbrack + \frac{\theta_{1}}{\theta_{2}}\ \beta_{2}\ {T''}_{1}\left( 3 \right) \\ + 2\frac{{\overline{c}}_{c} \Delta t }{ \Delta z }\left\lbrack \theta_{1}\ \left| w_{1} \right|{T'}_{1} + \theta_{2}\left| w_{2} \right|{T'}_{2}\ \right\rbrack \\ \end{matrix}\end{split}\]

(3.3‑83c)

\[D_{3} = \frac{\theta_{1}}{\theta_{2}}\beta_{2}\ {T''}_{1}\left( 2 \right) + {T''}_{1} \left( 3 \right)\ \left\lbrack \alpha_{1} - \frac{\theta_{1}}{\theta_{2}}\ \left( \beta_{2} + \beta_{3} \right) \right\rbrack + \frac{\theta_{1}}{\theta_{2}}\ \beta_{3}\ {T''}_{1}\left( 4 \right)\]

(3.3‑83d)

\[D_{4} = \frac{\theta_{1}}{\theta_{2}}\beta_{3}\ {T''}_{1}\left( 3 \right) + \ {T''}_{1} \left( 4 \right)\ \left\lbrack \alpha_{4} - \frac{\theta_{1}}{\theta_{2}}\ \left( \beta_{3} + \beta_{4} \right) \right\rbrack + S_{\text{pr}}\ Q_{chch} \Delta t\]

(3.3‑84a)

\[{T''}_{1}\left( 1 \right) = T_{\text{e}1}\left( jp \right)\]

(3.3‑84b)

\[{T''}_{1}\left( 2 \right) = {\overline{T}}_{\text{c}1}\left( jc \right)\]

(3.3‑84c)

\[{T''}_{1}\left( 3 \right) = T_{\text{sti}1}\left( jc \right)\]

and

(3.3‑84d)

\[{T''}_{1}\left( 4 \right) = T_{\text{sto}1}\left( jc \right)\]

This tri-diagonal matrix equation is solved in the same manner as in Section 3.3.1.2 above. For step 3, Eq. 3.3-70 is rewritten as

(3.3‑85)

\[T_{g2}\ = \frac{T_{g1} + d'\ s'}{1 + d'\ \theta_{2}}\]

where

(3.3‑86)

\[d'\ = \frac{2\pi\ r_{\text{brp}}\ H_{\text{eg}} \Delta t }{\left( \rho c \right)_{g}\ A_{g}}\]

and

(3.3‑87)

\[s' = \frac{\sum_{\text{jp}}{\left\{ \theta_{1}\ \left( T_{\text{c}1}\left( jp \right) - T_{\text{g}1} \right) + \theta_{2}\ T_{\text{e}2}\ \left( jp \right) \right\}\Delta z\left( jp \right)}}{\sum_{\text{jp}}{\Delta z\left( jp \right)}}\]

3.3.4. Order of Solution

For a time step, the coolant flow rates are calculated before any temperatures are calculated. Extrapolated coolant temperatures are used to obtain temperature-dependent coolant properties for the flow-rate calculations. Section 3.9 describes the pre-voiding coolant flow-rate calculations.

The order in which the temperature calculations are carried out depends on whether the coolant flow is up or down. In either case, the calculation goes in the direction of the flow. For upward flow, the calculation starts at the subassembly inlet. The coolant temperature at the first coolant node is set equal to the inlet temperatures, \(T_{\text{in}}\):

(3.3‑88)

\[T_{\text{c}2}\left( 1 \right) = T_{\text{in}}\]

The inlet temperature is supplied by the primary loop calculation, as discussed in Chapter 5. For each axial coolant node, \(jc\), the coolant temperature, \(T_{\text{c}2} (jc)\), at the bottom of the node is used as input for the simultaneous calculation of temperatures at all radial nodes. The solutions in Section 3.3.1, 3.3.2, and 3.3.3 provide \({\overline{T}}_{\text{c}2}\ \left( jc \right)\), the average coolant temperature for the axial node. The \({\overline{T}}_{\text{c}2} \left( jc + 1 \right)\) is obtained from

(3.3‑89)

\[T_{c2} \left( jc + 1 \right) = 2{\overline{T}}_{\text{c}2} \left( jc \right) - T_{\text{c}2} \left( jc \right)\]

This coolant temperature at the top of the node \(jc\) is the coolant inlet temperature used as input for the calculation at node \(jc + 1\).

If the flow is downward, the process is the same, except that the calculation starts at the top of the subassembly and works down. The coolant reentry temperatures, \(T_{\text{up}\mathcal{l}}\), described in Section 3.3.6 is used as the starting point for the last coolant node MZC:

(3.3‑90)

\[T_{\text{c}2} \left( \text{MZC} \right) = T_{\text{upl}}\]

For each coolant node, \(jc\), \(T_{\text{c}2} (jc + 1)\) is used as input to the calculation of all radial nodes. The solutions in Section 3.3.1, 3.3.2, and 3.3.3 again provide \({\overline{T}}_{\text{c}2} \left( jc \right)\). Then \(T_{\text{c}2} \left( jc \right)\) is obtained from

(3.3‑91)

\[T_{\text{c}2} \left( jc \right) = 2{\overline{T}}_{\text{c}2} \left( jc \right) - T_{\text{c}2} \left( jc + 1 \right)\]

3.3.5. Melting of Fuel or Cladding

As discussed in Section 3.3.1.1, melting of both fuel and cladding is treated with a melting range form a solidus temperature, \(T_{\text{sol}}\), to a liquidus temperature, \(T_{\text{liq}}\), rather than using a sharp melting temperature. Between the solidus and the liquidus, an effective specific heat, \(c_{\text{m}}\), based on the heat of fusion is used, as in Eq. 3.3-3. In the actual temperature calculations for a time step, the heat of fusion is neglected. Then, at the end of the step the temperatures are modified to account for the heat of fusion at any radial node that is going through the melting range. A number of different cases are considered, depending on the relationships between \(T_1\), the temperature at the beginning of the step, and \(T_2\), the temperature calculated for the end of the step, ignoring melting, \(T_{\text{sol}}\) and \(T_{\text{liq}}\). In all cases, \({T''}_{2}\) is the final adjusted temperature at the end of the step, and \({T'}_{2}\) would be the final adjusted temperature if it did not go beyond the melting range.

Case 1: \(T_{1} < T_{\mathrm{\text{sol}}}\), \(T_{2} > T_{\mathrm{\text{sol}}}\)

In this case, an adjusted temperature,\({T'}_{2}\), is calculated as

(3.3‑92)

\[{T'}_{2} = T_{\text{sol}} + \left( T_{2}\ - T_{\text{sol}} \right) \frac{c}{c_{\text{m}}}\]

where c is the normal specific heat that was used in the calculation of \(T_2\). Then,

(3.3‑93a-b)

\[\begin{split} {T}'_{2} = \begin{cases} T_{\text{liq}} + \left( {T'}_{2}\ - T_{\text{liq}} \right) \frac{c_{\text{m}}}{c} & \text{if}\ \ {T'}_{2}\ \ > \ \ T_{\text{liq}} \\ {T'}_{2} & \text{otherwise} \\ \end{cases}\end{split}\]

In essence, Eq. 3.3-92 divides the energy above the solidus by \(c_{\text{m}}\) to get the temperature above the solidus; and Eq. 3.3-93 divides any energy above the liquidus by c to get the temperature above the liquidus.

Case 2: \(T_{1} > T_{\mathrm{\text{liq}}}\), \(T_{2} < T_{\mathrm{\text{liq}}}\)

In this case,

(3.3‑94)

\[{T'}_{2} = T_{\text{liq}} + \left( T_{2}- T_{\text{liq}} \right) \frac{c}{c_{\text{m}}}\]

(3.3‑95)

\[\begin{split} {T}'_{2} = \begin{cases} T_{\text{sol}} + \left( {T'}_{2}\ - T_{\text{sol}} \right) \frac{c_{\text{m}}}{c} & \text{if}\ \ {T'}_{2}\ \ > \ \ T_{\text{sol}} \\ {T'}_{2} & \text{otherwise} \\ \end{cases}\end{split}\]

Case 3: \(T_{\mathrm{\text{liq}}} \geq T_{1} \geq T_{\mathrm{\text{sol}}}\)

In this case

(3.3‑96)

\[{T'}_{2} = T_{1} + \left( T_{2} - T_{1} \right) \frac{c}{c_{\text{m}}}\]

(3.3‑97a-b)

\[\begin{split}{T'}_{2} = \begin{cases} T_{\text{liq}} + \left( {T'}_{2} - T_{\text{liq}} \right) \frac{c_{m}}{c} & \text{if }{T'}_{2}\ \ > \ \ T_{\text{liq}} \\ T_{\text{sol}} + \left( {T'}_{2} - T_{\text{sol}} \right) \frac{c_{m}}{c} & \text{if }{T'}_{2}\ \ < \ \ T_{\text{sol}} \\ {T'}_{2} & \text{otherwise} \\ \end{cases}\end{split}\]

3.3.6. Coolant Inlet and Re-entry Temperature

The coolant inlet temperature at the subassembly inlet and the re-entry temperature at the subassembly outlet are determined mainly by the coolant plenum temperatures calculated in PRIMAR-4; but, in addition, mixing zones are modeled at the inlet and outlet of each channel. Therefore, the temperature of coolant entering a subassembly is based on the temperature in the part of the plenum in the immediate vicinity of the end of the subassembly, and the reentry temperature soon after an expulsion is based on both the bulk plenum temperature and the temperature of the coolant that was recently expelled.

The mixing mode uses a mass, \(M_{\text{mix}}\), of the coolant in the mixing volume, a specific heat, \(C_{\text{mix}}\), of the coolant, and a time constant, \(\tau_{\text{mix}}\), for heat transfer or mixing between the mixing volume and the bulk plenum coolant. If all temperatures and flows are constant, then the mixing volume temperature, \(T_{\text{mix}}\), is assumed to approach an equilibrium value asymptotically with an exponential decay. Figure 3.3.1 shows the model for the outlet mixing volume.

If \(T_{\text{mix}1}\) is the mixing volume temperature at the beginning of a time step, the \(T_{\text{mix}2}\) is the value at the end, then

(3.3‑98)

\[T_{\text{mix}2} = T_{\text{eq}} + \left( T_{\text{mix}1} - T_{\text{eq}} \right) e^{- \frac{\Delta t}{\tau}}\]

For the outlet plenum,

(3.3‑99)

\[\frac{1}{\tau} = \frac{1}{\tau_{\text{mix}}} + \frac{\left| \overline{w} \right|}{M_{\text{mix}}}\]

where \(\overline{w}\) is the average coolant flow rate at the subassembly outlet. The equilibrium temperature is

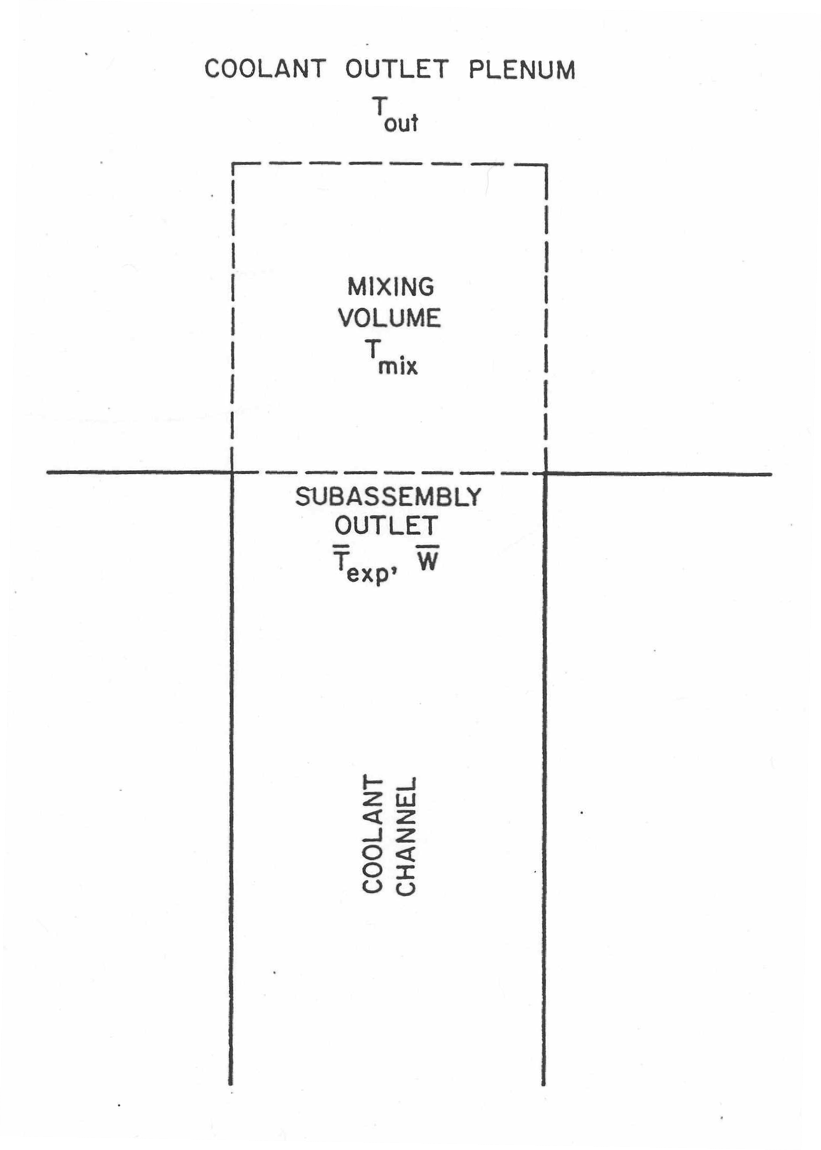
Figure 3.3.1 Coolant Re-entry Temperature Model

(3.3‑100a-b)

\[\begin{split}T_{\text{eq}} = \begin{cases} T_{\text{out}} & \text{if} \ \ \overline{w} \ \ \leq \ \ 0 \\ \left( \frac{T_{\text{out}}}{\tau_{\text{mix}}} + \frac{\overline{w} \overline{T}_{\text{exp}}}{M_{\text{mix}}} \right) \tau & \text{if} \ \ \overline{w} \ \ > \ \ 0 \\ \end{cases}\end{split}\]

where \({\overline{T}}_{\exp}\) is the average temperature of the sodium expelled from the top of the subassembly into the mixing volume during the time step. \(T_{\text{out}}\) is the bulk temperature in the outlet plenum. For the inlet plenum, the same equations are used except that \(\overline{w}\) changes sign because positive flow results in flow from the inlet mixing volume into the subassembly inlet. For the inlet, Eqs. 3.3-100a and 3.3-100b become

(3.3‑101a-b)

\[\begin{split}T_{\text{eq}} = \begin{cases} T_{\text{in}} & \text{if} \ \ \overline{w} \ \ \leq \ \ 0 \\ \left( \frac{T_{\text{in}}}{\tau_{\text{mix}}} - \frac{\overline{w} \overline{T}_{\text{exp}}}{M_{\text{mix}}} \right) \tau & \text{if} \ \ \overline{w} \ \ > \ \ 0 \\ \end{cases}\end{split}\]

where \(T_{\text{in}}\) is the bulk temperature in the inlet plenum.

The coolant inlet and reentry temperature calculations described above are used in both the pre-voiding module and the boiling module except when a vapor bubble has blown out of the top of the channel. In this case, the condensation of vapor in the outlet plenum raises the temperature in the mixing volume. A two-step process is used for each time step. In the first step, vapor condensation raises the mixing volume temperature. In the second step, heat transfer or mixing with the bulk plenum coolant is accounted for. For the first step, a condensation heat-transfer time constant, \(\tau_{\text{c}}\), is calculated as

(3.3‑102)

\[\tau_{\text{c}} = \frac{M_{\text{mix}}\ C_{\text{mix}}}{h_{\text{cond}}\Delta Z_{\text{v}}\ p_{\text{er}}}\]

where \(h_{\text{cond}}\) is the vapor condensation heat-transfer coefficient, \(\Delta Z_{\text{v}}\) is the length of the vapor bubble beyond the subassembly outlet, and \(p_{\text{er}}\) is the bubble perimeter or surface area per unit length. The value of \(p_{\text{er}}\) is taken from the coolant channel dimensions in the top node below the subassembly outlet. For step 1, the new mixing volume temperature, \(T_{\text{new}}\), is calculated as

(3.3‑103)

\[T_{\text{new}} = {\overline{T}}_{\text{v}} + \left( T_{mix1} - {\overline{T}}_{\text{v}} \right) e^{- \frac{\Delta t}{\tau_{\text{c}}}}\]

where \(\overline{T}_{v}\) is the average vapor temperature in the part of the bubble above the subassembly outlet. In the second step, the final mixing volume temperature is calculated as

(3.3‑104)

\[T_{\text{mix}2} = T_{\text{new}} + \left( T_{\text{out}} - T_{\text{new}} \right) \left( 1 - e^{- \frac{\Delta t}{\tau_{\text{mix}}}} \right)\]