5.4.3. Bypass Channels

5.4.3.1. Introduction

The purpose of the bypass channel is to model components, like control rods and radial shields, that do not need the detailed treatment of a SAS channel. The bypass channel is then considered a part of the primary loop and is not included in the SAS channel core treatment.

The bypass channel is shown schematically in Figure 5.4.3. It is modeled as two reflectors, A and B, a coolant channel, C, and a duct wall, D. The bypass channel is divided into from 1 to 7 vertical sections, with temperatures of the two reflectors and duct wall taken at the centers of each vertical section and the coolant temperatures taken at the interfaces of each vertical section. The outside surface of reflector A is taken as adiabatic, and heat conduction in the axial direction is neglected. The outside surface of the duct wall can be in contact with a heat sink that represents neighboring subassemblies, as discussed in Section 5.4.1.

Heat sources are included in each of the two regions of reflectors A and B and also in the duct wall, taken as region 3. A vertical power shape for the heat source can be assigned to the sections in the three regions. Two heat sources are included, a neutron heat source and a decay heat source. The neutron heat source arises from fissions caused by neutrons, and is a fraction of the reactor power. The decay heat source arises from fission product decay which produces no neutrons.

A heat balance equation is written for each vertical section of the bypass channel, and the temperature changes during a time step are computed. The choice of the degree of implicitness used in the solution is discussed in Section 5.2.4 and in Section 2.8.1 in Chapter 2. The temperatures at the beginning of a time step are known, and the coolant mass flow rates at the beginning and at the end of a time step are known from the hydraulics calculations described in Section 5.2. Also, the heat sources during the time step are known. As a result, a set of four simultaneous equations is solved for each vertical section in turn for the length of the bypass channel. In the case of flow reversal, the series of solutions is carried out along the bypass channel in the opposite direction. The temperature changes during the time step are added to the corresponding temperatures at the beginning of the time step, and the final values are then stored in COMMON blocks.

5.4.3.2. Basic Equations

A vertical section of reflector A, with the outside surface assumed adiabatic and with axial thermal conduction ignored, is in thermal contact with only the adjacent section of reflector B. The heat balance equation for the section in A is:

(5.4-49)\[ \left( \rho c \right)_{\text{A}}\Delta z P_{\text{A}}d_{\text{A}} \frac{\partial \text{T}_{\text{A}}}{\partial \text{t}} = \Delta z P_{\text{A}}H_{\text{AB}}\left( T_{\text{B}} - T_{\text{A}} \right) + \Delta z P_{\text{A}} d_{\text{A}} Q_{\text{A}}\]

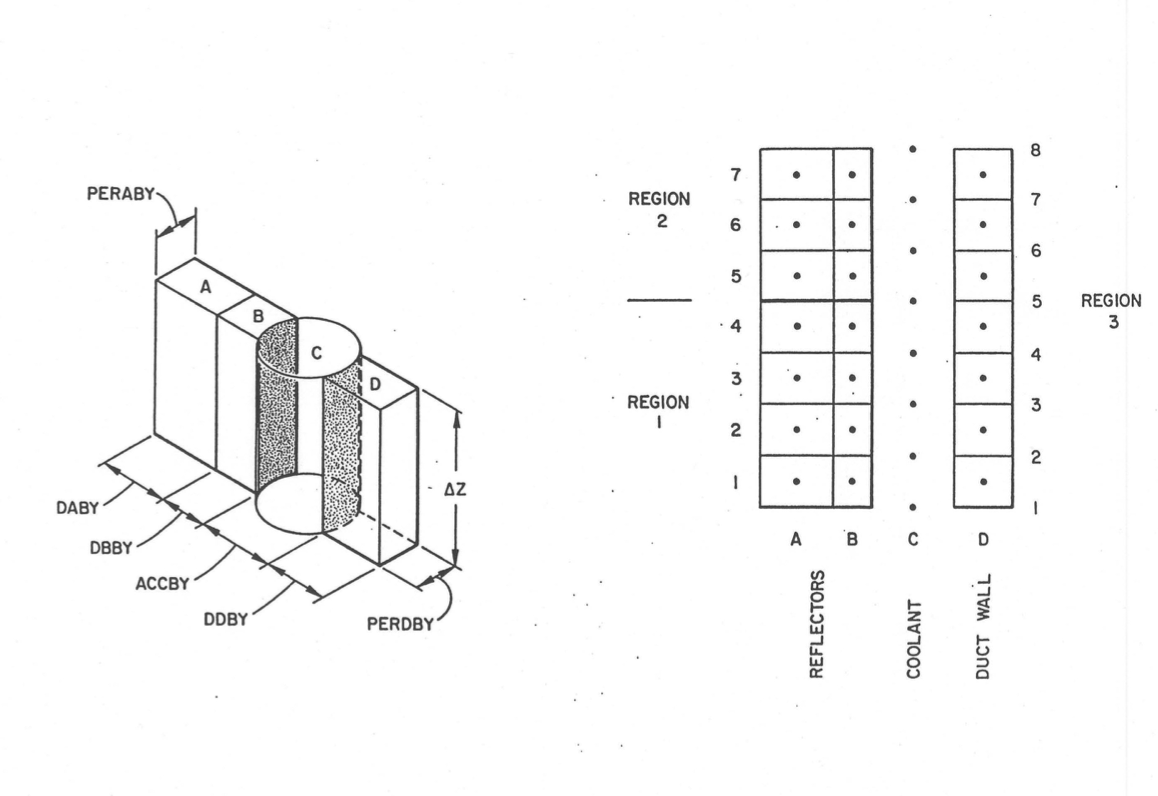
Figure 5.4.3 Bypass Channel Schematic.

with

(5.4-50)\[ \frac{1}{H_{\text{AB}}} = \frac{d_{\text{A}}}{2k_{\text{A}}} + \frac{d_{\text{B}}}{2k_{\text{B}}}\]

(5.4-51)\[ \begin{aligned} Q_{\text{A}} = \frac{P_{\text{TOT}}Q_{\text{MULT}}}{\Delta z} f_{1} \frac{P_{\text{s}}}{P_{1}} \left( \gamma_{\text{N}1} + \gamma_{\text{D}1} \right) , && \text{Region 1} \end{aligned}\]

(5.4-52)\[ \begin{aligned} Q_{\text{A}} = \frac{P_{\text{TOT}}Q_{\text{MULT}}}{\Delta z} f_{2} \frac{P_{\text{s}}}{P_{2}} \left( \gamma_{\text{N}2} + \gamma_{\text{D}2} \right) , && \text{Region 2} \end{aligned}\]

where

\(\left( \rho c \right)_{\text{A}}\) = the reflector A density times specific heat

\(\Delta z\) = the height of the vertical section

\(P_{\text{A}}\) = the perimeter between reflectors A and B and between B and C

\(d_{\text{A}}\) = the thickness of reflector A

\(T_{\text{A}}\) = the temperature of the vertical section of reflector A

\(T_{\text{B}}\) = the temperature of the vertical section of reflector B

\(d_{\text{B}}\) = the thickness of reflector B

\(k_{\text{A}}\) = the thermal conductivity of reflector A

\(k_{\text{B}}\) = the thermal conductivity of reflector B

\(Q_{\text{A}}\) = the heat source in the vertical section of reflector A

\(P_{\text{TOT}} Q_{\text{MULT}}\) = the reactor power for this time step

\(f_1\) = the fraction of the reactor power distributed in reflector A in Region 1 of the bypass channel

\(f_2\) = the fraction of the reactor power distributed in reflector A in Region 2 of the bypass channel

\(P_{\text{s}}\) = the power shape assigned to the vertical sections

\(P_1\) = the power shape normalization for Region 1

\(\gamma_{\text{N}1}\) = the fraction of the reactor power in Region 1 attributed to neutron heating

\(\gamma_{\text{D}1}\) = the fraction of the reactor power in Region 1 attributed to decay heating

\(P_2\) = the power shape normalization for Region 2

\(\gamma_{\text{N}2}\) = the fraction of the reactor power in Region 2 attributed to neutron heating

\(\gamma_{\text{D}2}\) = the fraction of the reactor power in Region 2 attributed to decay heating

The density times specific heat for reflector A and the thermal conductivities for reflectors A and B are assumed to be independent of temperature. The reactor power for the current time step, \(P_{\text{TOT}} Q_{\text{MULT}}\), is described in Chapter 4. The power shape, \(P_{\text{s}}\), for each vertical section is an input value, and the code calculates a normalization factor for each region in the bypass channel. The decay heat produced in a section of the reflector or duct wall is taken, in the current version of the code, to be a fraction of the reactor power, just as is the neutron heating. These fractions, the \(\gamma\)’s, are input numbers, as are \(P_{\text{s}}\), \(f_1\), and \(f_2\).

The heat balance for a vertical section of reflector B, which is in thermal contact with the adjacent sections of reflector A and of the coolant, is

(5.4-53)\[\begin{split}\left( \rho c \right)_{\text{B}}\Delta z P_{\text{A}} d_{\text{B}} \frac{\partial \text{T}_{\text{B}}}{\partial \text{t}} = \Delta z P_{\text{A}} H_{\text{AB}} \left( T_{\text{A}} - T_{\text{B}} \right) \\ + \Delta z P_{\text{A}} H_{\text{BC}} \left( {\overline{T}}_{\text{C}} - T_{\text{B}} \right) \\ + \Delta z P_{\text{A}} d_{\text{B}} Q_{\text{B}}\end{split}\]

with

(5.4-54)\[\frac{1}{H_{\text{BC}}} = \frac{1}{h_{\text{C}}} + \frac{d_{\text{B}}}{2k_{\text{B}}}\]

(5.4-55)\[h_{\text{C}} = \frac{{\overline{k}}_{\text{c}}}{D_{\text{h}}} \left\lbrack C_{1} \left( \frac{D_{\text{h}} \left| w_{\text{c}} \right| c_{\text{C}}}{A_{\text{C}} {\overline{k}}_{\text{c}}} \right)^{C_{2}} + C_{3} \right\rbrack\]

(5.4-56)\[{\overline{T}}_{\text{c}} = \frac{1}{2} \left\lbrack T_{\text{c}}\left( j \right) + T_{\text{c}} \left( j + 1 \right) \right\rbrack\]

(5.4-57)\[\begin{aligned} Q_{\text{B}} = \frac{P_{\text{TOT}}Q_{\text{MULT}}}{\Delta z} \left( 1 - f_{1} \right) \frac{P_{\text{s}}}{P_{1}} \left( \gamma_{\text{N}1} + \gamma_{\text{D}1} \right) , && \text{Region 1} \end{aligned}\]

(5.4-58)\[\begin{aligned} Q_{\text{B}} = \frac{P_{\text{TOT}}Q_{\text{MULT}}}{\Delta z} \left( 1 - f_{2} \right) \frac{P_{\text{s}}}{P_{2}} \left( \gamma_{\text{N}2} + \gamma_{\text{D}2} \right) , && \text{Region 2} \end{aligned}\]

where

\(\left( \rho c \right)_{\text{B}}\) = the reflector B density times specific heat

\(Q_{\text{B}}\) = the heat source in the vertical section of reflector B

\(T_{\text{c}} \left( j \right)\) = the coolant temperature at the lower end of the vertical section

\(T_{\text{c}} \left( j+1 \right)\) = the coolant temperature at the upper end of the vertical section

\({\overline{k}}_{\text{c}}\) = the coolant thermal conductivity at the temperature \({\overline{T}}_{\text{c}}\)

\({\overline{c}}_{\text{c}}\) = the coolant specific heat at the temperature \({\overline{T}}_{\text{c}}\)

\(\left| w \right|\) = the absolute value of the coolant mass flow rate

\(D_{\text{k}}\) = the coolant channel hydraulic diameter

\(A_{\text{C}}\) = the coolant flow area

\(C_1\), \(C_2\), \(C_3\) = user-supplied correlation coefficients

The remaining symbols are the same as defined above.

The heat balance for a vertical section of the coolant, which is in thermal contact with the adjacent sections of reflector B and the duct wall D, is

(5.4-59)\[\begin{split}A_{\text{C}}\Delta z {\overline{\rho}}_{\text{C}} {\overline{c}}_{\text{C}} \frac{\partial {\overline{\text{T}}}_{\text{C}}}{\partial \text{t}} + A_{\text{c}}\Delta z \frac{\partial}{\partial \text{z}} \left( \frac{w{\overline{c}}_{\text{C}}}{A_{\text{C}}} {\overline{T}}_{\text{C}} \right) = \Delta z P_{\text{A}} H_{\text{BC}} \left( T_{\text{B}} - {\overline{T}}_{\text{C}} \right) \\ + \Delta z P_{\text{D}} H_{\text{CD}} \left( T_{\text{D}} - {\overline{T}}_{\text{C}} \right)\end{split}\]

with

(5.4-60)\[\frac{1}{H_{\text{CD}}} = \frac{1}{h_{\text{C}}} + \frac{d_{\text{D}}}{2k_{\text{D}}}\]

where

\({\overline{\rho}}_{\text{C}}\) = the coolant density evaluated at temperature \({\overline{T}}_{\text{C}}\)

\(w\) = the coolant mass flow rate

\(P_{\text{D}}\) = the perimeter between the coolant and the duct wall

\(d_{\text{D}}\) = the thickness of the duct wall

\(k_{\text{D}}\) = the thermal conductivity of the duct wall

\(T_{\text{D}}\) = the temperature of the vertical section of the duct wall

The thermal conductivity of the duct wall is assumed to be independent of temperature. The remaining symbols are the same as already defined.

The heat balance for a vertical section of the duct wall, which, is in thermal contact with the coolant and an external heat sink is

(5.4-61)\[\begin{split}\left( \rho c \right)_{\text{D}} \Delta z P_{\text{D}} d_{\text{D}} \frac{\partial \text{T}_{\text{D}}}{\partial \text{t}} = \Delta z P_{\text{D}} H_{\text{CD}} \left( {\overline{T}}_{\text{C}} - T_{\text{D}} \right) \\ + \Delta z P_{\text{D}} d_{\text{D}} Q_{\text{D}} + \Delta z \left( hA \right)_{\text{snk}}\left( T_{\text{snk}} - T_{\text{D}} \right)\end{split}\]

with

(5.4-62)\[Q_{D} = \frac{P_{\text{TOT}}Q_{\text{MULT}}}{\Delta z} \frac{P_{\text{s}}}{P_{3}} \left( \gamma_{\text{N}3} + \gamma_{\text{D}3} \right)\]

where

\(\left( \rho c \right)_{\text{D}}\) = the duct wall density times specific heat

\(Q_{\text{D}}\) = the heat source in the vertical section of the duct wall

\(P_3\) = the power shape normalization for the duct wall

\(\gamma_{\text{N}3}\) = the fraction of the reactor power in the duct wall attributed to neutron heating

\(\gamma_{\text{D}3}\) = the fraction of the reactor power in the duct wall attributed to decay heating

\(T_{\text{snk}}\) = the temperature of the heat sink outside the duct wall

\(\left( hA \right)_{\text{snk}}\) = the heat transfer coefficient times area per unit height for heat transfer to the sink

The remaining symbols are the same as already defined.

5.4.3.3. Finite Difference Equations and Solution

The four equations 5.4-37, 5.4-41, 5.4-47, and 5.4-49 are a set of simultaneous equations that can be solved for one vertical section of the bypass channel. If the coolant flow is upward (normal flow), then the coolant temperature at the bottom of the lowest vertical section is known, and the coolant temperature at the top of the vertical section as well as the reflector and duct wall temperatures are solved for. This process is repeated up the bypass channel for each vertical section. If, on the other hand, the coolant flow is downward (reversed flow), the coolant temperature at the top of the uppermost vertical section is known, and the coolant temperature at the bottom of the section as well as the reflector and duct wall temperatures are solved for. This process is then repeated down the bypass channel for each vertical section.

First, however, the above four equations are converted to finite difference equations and the temperatures at the end of the time step are solved for. The differencing is accomplished by replacing time derivatives by

(5.4-63)\[\begin{aligned} \frac{\partial \text{T}}{\partial \text{t}} = \frac{\Delta T}{\Delta t} && ; && \Delta T = T_{4} = T_{3} \end{aligned}\]

where \(T_3\) and \(T_4\) are the temperatures at the beginning and at the end of the time interval \(\Delta t\). The temperatures \(T_1\) and \(T_2\) usually denote the beginning and end of a PRIMAR time step, and any subdivision of that time step is denoted by 3 and 4. Space derivatives are taken in the direction of flow. If the flow is up,

(5.4-64)\[\frac{\partial \text{T}}{\partial \text{z}} = \frac{T\left( j + 1 \right) - T\left( j \right)}{\Delta z}\]

and if the flow is down,

(5.4-65)\[\frac{\partial \text{T}}{\partial \text{z}} = \frac{T\left( j \right) - T\left( j + 1 \right)}{\Delta z}\]

where \(T \left( j \right)\) and \(T \left( j+1 \right)\) are the temperatures evaluated at the two interfaces of the vertical section of height \(\Delta z\). The degree of implicitness is introduced by replacing \(T\) with

(5.4-66)\[T = \theta_{1} T_{3} + \theta_{2} T_{4}\]

where \(\theta_1 + \theta_2 = 1\), as described in Section 5.2.4 and in Section 2.8.1 in Chapter 2, and \(T_3\) and \(T_4\) are the temperatures at the beginning and at the end of the time interval \(\Delta t\).

After making the above substitutions, the equations for the temperatures at the end of the time interval \(\Delta t\) for the \(j\)-th vertical section of the bypass channel can be written as:

(5.4-67)\[\begin{split}\begin{pmatrix} \alpha _{1} + \beta _{1} & - \beta _{1} & 0 & 0 \\ - \beta _{1} & \alpha _{2} + \beta _{1} + \beta _{2} & - \beta _{2} & 0 \\ 0 & - \beta _{2} & \alpha _{3} + \beta _{2} + \beta _{3} & - \beta _{3} \\ 0 & 0 & - \beta _{3} & \alpha _{4} + \beta _{3} + \beta _{4} \\ \end{pmatrix} \begin{pmatrix} T_{\text{A}4} \\ T_{\text{B}4} \\ {\overline{T}}_{\text{C}4} \\ T_{\text{D}4} \\ \end{pmatrix} = \begin{pmatrix} D_{1} \\ D_{2} \\ D_{3} \\ D_{4} \\ \end{pmatrix}\end{split}\]

with

(5.4-68)\[\alpha_{1} = \left( \rho c \right)_{\text{A}} P_{\text{A}} d_{\text{A}}\]

(5.4-69)\[\alpha_{2} = \left( \rho c \right)_{\text{B}} P_{\text{B}} d_{\text{B}}\]

(5.4-70)\[\alpha_{3} = A_{\text{c}} \overline{\rho}\left( j \right) \overline{c}\left( j \right) + \frac{2\overline{c}\left( j \right)}{\Delta z\left( j \right)} \theta_{2} \Delta t \left| w_{4} \right|\]

(5.4-71)\[\alpha_{4} = \left( \rho c \right)_{\text{D}} P_{\text{D}} d_{\text{D}}\]

(5.4-72)\[\beta_{1} = P_{\text{A}} H_{\text{AB}} \Delta t \theta_{2}\]

(5.4-73)\[\beta_{2} = P_{\text{A}} H_{\text{BC}} \Delta t \theta_{2}\]

(5.4-74)\[\beta_{3} = P_{\text{A}} H_{\text{DC}} \Delta t \theta_{2}\]

(5.4-75)\[\beta_{4} = \left( hA \right)_{\text{snk}} \Delta t \theta_{2}\]

(5.4-76)\[\begin{split}D_{1} = \left\lbrack \left( \rho c \right)_{\text{A}} P_{\text{A}} d_{\text{A}} - P_{\text{A}} H_{\text{AB}} \Delta t \theta_{1} \right\rbrack T_{\text{A}3} \\ + P_{\text{A}} H_{\text{AB}} \Delta t \theta_{1} T_{\text{B}3} + \Delta t Q_{\text{A}}\end{split}\]

(5.4-77)\[\begin{split}D_{2} = P_{\text{A}} H_{\text{AB}} \Delta t \theta_{1} T_{A3} \\ + \left\lbrack \left( \rho c \right)_{\text{B}} P_{\text{B}} d_{\text{B}} - P_{\text{A}} H_{\text{AB}} \Delta t \theta_{1} - P_{\text{A}} H_{\text{BC}} \Delta t \theta_{1} \right\rbrack T_{\text{B}3} \\ + P_{\text{A}} H_{\text{AB}} \Delta t \theta_{1} {\overline{T}}_{\text{C}3} + \Delta t Q_{\text{B}}\end{split}\]

(5.4-78)\[\begin{split}D_{3} = P_{\text{A}} H_{\text{DC}} \Delta t \theta_{1} T_{\text{B}3} \\ + \left\lbrack A_{\text{c}} \overline{\rho}\left( j \right) \overline{c}\left( j \right) - \frac{2 \overline{c}\left( j \right)}{\Delta z\left( j \right)} \theta_{1} \Delta t \left| w_{3} \right| - P_{\text{A}} H_{\text{BC}} \Delta t \theta_{1} - P_{\text{D}}H_{\text{DC}}\Delta t \theta_{1} \right\rbrack {\overline{T}}_{\text{C}3} \\ + P_{\text{D}} H_{\text{DC}} \Delta t \theta_{1} T_{\text{D}3} + \frac{2 \overline{c}\left( j \right)}{\Delta z\left( j \right)} \Delta t \left\lbrack \theta_{1} \left| w_{3} \right| T_{\text{C}3} + \theta_{2} \left| w_{4} T_{\text{C}4} \right| \right\rbrack\end{split}\]

(5.4-79)\[\begin{split}D_{4} = P_{\text{D}} H_{\text{DC}} \Delta t \theta_{1} {\overline{T}}_{\text{C}3} \\ + \left\lbrack \left( \rho c \right)_{\text{D}} P_{\text{D}} d_{\text{D}} - P_{\text{D}} H_{\text{DC}} \Delta t \theta_{1} - \left( hA \right)_{\text{snk}} \Delta t \theta_{1} \right\rbrack T_{\text{D}3} + \Delta t Q_{\text{D}} \\ + \left( hA \right)_{\text{snk}} \Delta t T_{\text{snk}}\end{split}\]

The matrix Eq. (5.4-67) is solved by standard tri-diagonal inversion in subroutine INVRT3, and the node temperatures of reflectors A and B and duct wall D and the interface temperatures of the coolant are stored in COMMON blocks. In addition, the gravity head of the bypass element is calculated, using the new coolant temperatures, and also stored in COMMON blocks.

5.4.3.4. Steady-State Bypass Channels

The steady-state bypass temperature calculations, performed in subroutine SSBYPS, differ from the transient calculations in that the time derivative terms in Eq. (5.4-49), Eq. (5.4-53), Eq. (5.4-59), and Eq. (5.4-61) are set to zero and in that the steady-state power input into the reflectors and duct wall for each vertical section must be conducted to the coolant in that section. The coolant temperatures are calculated at the interfaces of each vertical section, marching up the bypass channel and iterating over the temperature-dependent thermal properties. From these coolant temperatures, the node temperatures of the reflectors and duct wall are then determined. In addition, the gravity head is calculated from the average coolant density for the whole channel, and the power normalization factors are calculated for all three regions.